九年级上册+九下第一单元沪科版数学期末复习(pdf、无答案)
文档属性
| 名称 | 九年级上册+九下第一单元沪科版数学期末复习(pdf、无答案) | 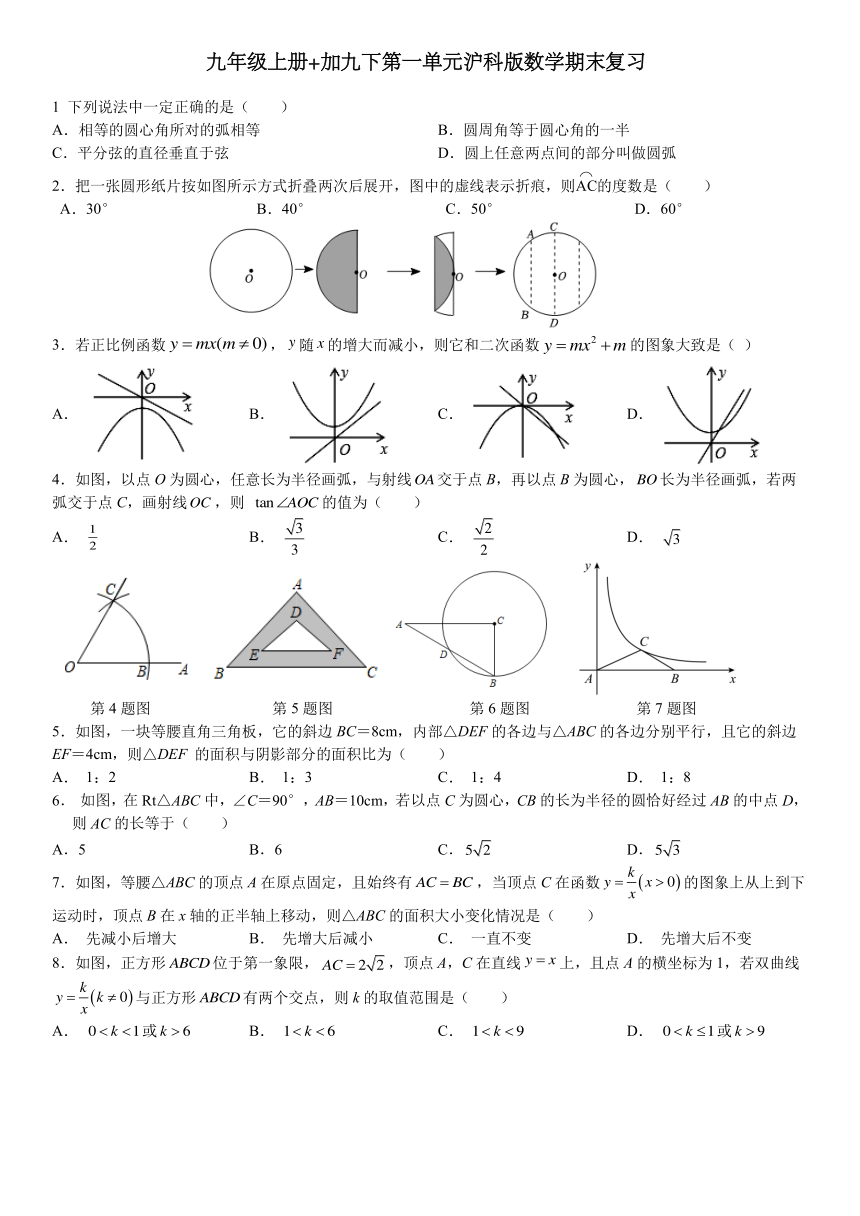 | |
| 格式 | zip | ||
| 文件大小 | 552.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-28 15:11:49 | ||
图片预览


文档简介
九年级上册+加九下第一单元沪科版数学期末复习
1下列说法中一定正确的是()
A.相等的圆心角所对的弧相等
B.圆周角等于圆心角的一半
C.平分弦的直径垂直于弦
D.圆上任意两点间的部分叫做圆弧
2.把一张圆形纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则AC的度数是()
A.30°
B.40
C.50
D.609
3.若正比例函数y=x(m≠O),y随×的增大而减小,则它和二次函数y=mx+m的图象大致是()
4.如图,以点O为圆心,任意长为半径画弧,与射线OA交于点B,再以点B为圆心,BO长为半径画弧,若两
弧交于点C,画射线Oc,则tan∠AOC的值为()
A.2
B.
2
D.3
C
B
B
A
B
第4题图
第5题图
第6题图
第7题图
5.如图,一块等腰直角三角板,它的斜边BC=8cm,内部△DEF的各边与△ABC的各边分别平行,且它的斜边
EF=4cm,则△DEF的面积与阴影部分的面积比为()
A.1:2
B.1:3
C.1:4
D.1:8
6.如图,在Rt△ABC中,∠C=90°,AB=10cm,若以点C为圆心,CB的长为半径的圆恰好经过AB的中点D,
则AC的长等于()
A.5
B.6
C.52
D.53
7.如图,等腰△ABC的顶点A在原点固定,且始终有AC=BC,当顶点C在函数y=二(X>O)的图象上从上到下
运动时,顶点B在x轴的正半轴上移动,则△ABC的面积大小变化情况是()
A.先减小后增大
B.先增大后减小
C.一直不变
D.先增大后不变
8.如图,正方形ABCD位于第一象限,AC=22,顶点A,C在直线y=X上,且点A的横坐标为1,若双曲线
y=K(k≠0)与正方形ABCD有两个交点,则k的取值范围是()
A.06
B.1C.1D.09
E
D
B
G
D
0
D
第8题图
第9题图
第10题图
9.如图,AB为⊙O的直径,点C是弧BE的中点.过点C作CD⊥AB于点G,交⊙O于点D,若BE=8,BG=
2,则⊙0的半径长是()
A.5
B.6.5
C.7.5
D.8
10.如图,正方形ABCD与正方形BEFG有公共顶点B,连接EC、GA,交于点O,GA与BC交于点P,连接OD、
OB,则下列结论一定正确的是()
①EC⊥AG:②△OBP∽△CAP:③OB平分∠CBG:④∠AOD=45°:
A.①③
B.①②③
C.②③
D.①②④
11.已知二次函数y=-x2+2x,当-1<×12.如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠AED=15°,则∠BCD的度数为
E
E
a
B
B D C
8
第12题图
第13题图
第15题图
13.如图,长度不变的“人字梯”放在水平地面上(AB=AC),当梯子的一边与地面所夹的锐角a为45°时,两梯
脚之间的距离BC为2米;当a=60°时,则梯子顶端距地面的高度AD上升了米.(结果保留根号)
14.如图1,P是⊙O外的一点,直线PO分别交⊙O于点A,B,则PA是点P到⊙O上的点的最短距离,
(1)探究一:如图2,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是CD上的
一个动点,连接AP,则AP的最小值是
(2)探究二:如图3,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△
AMW沿MN所在的直线翻折得到△A'MW,连接A'C,请求出A'C长度的最小值
(3)探究三,在正方形ABCD中,点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动,连
接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,若AD=4,试求出线段CP的最小值
(4)综合应用:如图5,平面直角坐标系中,分别以点A(一2,3),B(4,5)为圆心,以1,2为半径作⊙A,⊙
B,M,N分别是⊙A,⊙B上的动点,P为x轴上的动点,直接写出PM十PW的最小值为
0
图1
图2
图5
1下列说法中一定正确的是()
A.相等的圆心角所对的弧相等
B.圆周角等于圆心角的一半
C.平分弦的直径垂直于弦
D.圆上任意两点间的部分叫做圆弧
2.把一张圆形纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则AC的度数是()
A.30°
B.40
C.50
D.609
3.若正比例函数y=x(m≠O),y随×的增大而减小,则它和二次函数y=mx+m的图象大致是()
4.如图,以点O为圆心,任意长为半径画弧,与射线OA交于点B,再以点B为圆心,BO长为半径画弧,若两
弧交于点C,画射线Oc,则tan∠AOC的值为()
A.2
B.
2
D.3
C
B
B
A
B
第4题图
第5题图
第6题图
第7题图
5.如图,一块等腰直角三角板,它的斜边BC=8cm,内部△DEF的各边与△ABC的各边分别平行,且它的斜边
EF=4cm,则△DEF的面积与阴影部分的面积比为()
A.1:2
B.1:3
C.1:4
D.1:8
6.如图,在Rt△ABC中,∠C=90°,AB=10cm,若以点C为圆心,CB的长为半径的圆恰好经过AB的中点D,
则AC的长等于()
A.5
B.6
C.52
D.53
7.如图,等腰△ABC的顶点A在原点固定,且始终有AC=BC,当顶点C在函数y=二(X>O)的图象上从上到下
运动时,顶点B在x轴的正半轴上移动,则△ABC的面积大小变化情况是()
A.先减小后增大
B.先增大后减小
C.一直不变
D.先增大后不变
8.如图,正方形ABCD位于第一象限,AC=22,顶点A,C在直线y=X上,且点A的横坐标为1,若双曲线
y=K(k≠0)与正方形ABCD有两个交点,则k的取值范围是()
A.0
B.1
E
D
B
G
D
0
D
第8题图
第9题图
第10题图
9.如图,AB为⊙O的直径,点C是弧BE的中点.过点C作CD⊥AB于点G,交⊙O于点D,若BE=8,BG=
2,则⊙0的半径长是()
A.5
B.6.5
C.7.5
D.8
10.如图,正方形ABCD与正方形BEFG有公共顶点B,连接EC、GA,交于点O,GA与BC交于点P,连接OD、
OB,则下列结论一定正确的是()
①EC⊥AG:②△OBP∽△CAP:③OB平分∠CBG:④∠AOD=45°:
A.①③
B.①②③
C.②③
D.①②④
11.已知二次函数y=-x2+2x,当-1<×
E
E
a
B
B D C
8
第12题图
第13题图
第15题图
13.如图,长度不变的“人字梯”放在水平地面上(AB=AC),当梯子的一边与地面所夹的锐角a为45°时,两梯
脚之间的距离BC为2米;当a=60°时,则梯子顶端距地面的高度AD上升了米.(结果保留根号)
14.如图1,P是⊙O外的一点,直线PO分别交⊙O于点A,B,则PA是点P到⊙O上的点的最短距离,
(1)探究一:如图2,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是CD上的
一个动点,连接AP,则AP的最小值是
(2)探究二:如图3,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△
AMW沿MN所在的直线翻折得到△A'MW,连接A'C,请求出A'C长度的最小值
(3)探究三,在正方形ABCD中,点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动,连
接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,若AD=4,试求出线段CP的最小值
(4)综合应用:如图5,平面直角坐标系中,分别以点A(一2,3),B(4,5)为圆心,以1,2为半径作⊙A,⊙
B,M,N分别是⊙A,⊙B上的动点,P为x轴上的动点,直接写出PM十PW的最小值为
0
图1
图2
图5
