不等式的复习[上学期]

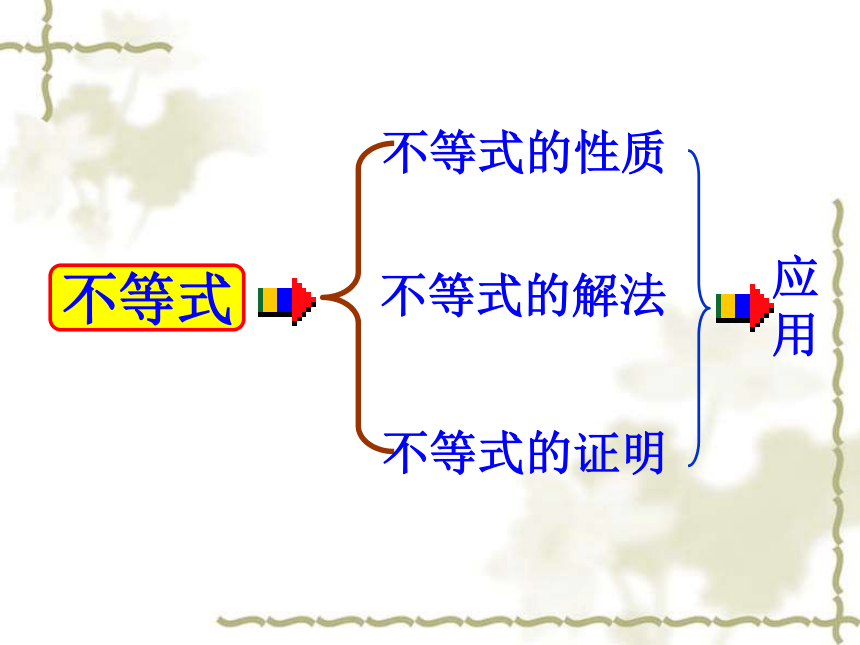
课件21张PPT。第六章：不等式期末复习不等式的性质不等式不等式的证明不等式的解法应
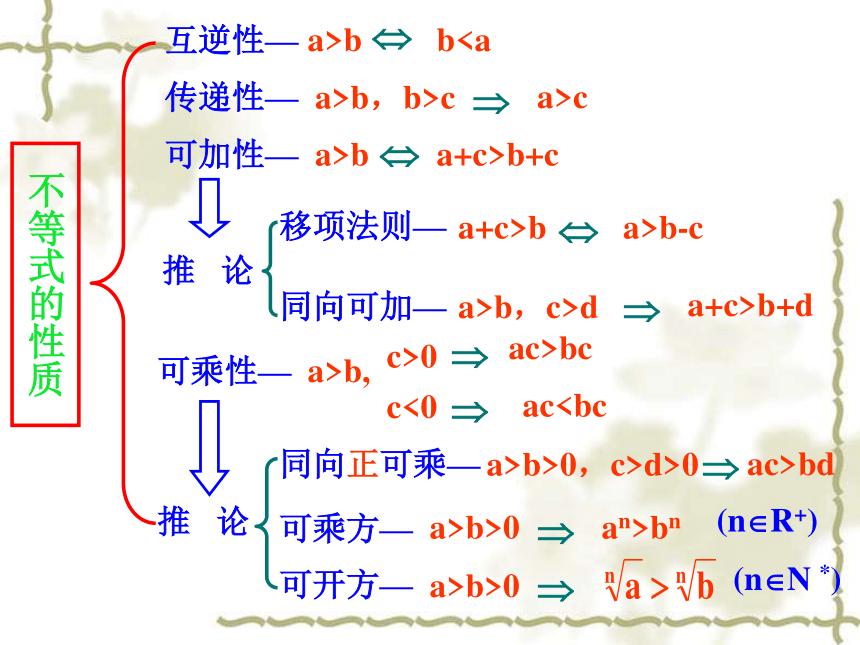
用不等式的性质互逆性—a>b传递性—a>b，b>c可加性—a>b移项法则—a+c>b同向可加—a>b，c>d可乘性—a>b,同向正可乘—a>b>0，c>d>0可乘方—a>b>0可开方—a>b>0(n?R+)(n?N *)?不等式的解法a>0，x>；a<0，x<(>0)ab或xg(x) 或 f(x)< - g(x)标根法注意点：①奇穿偶不穿； ②区间端点含否。绝对值不等式，还可用零点讨论法，或平方法，数形结合法等。不等式的解法作差、变形、
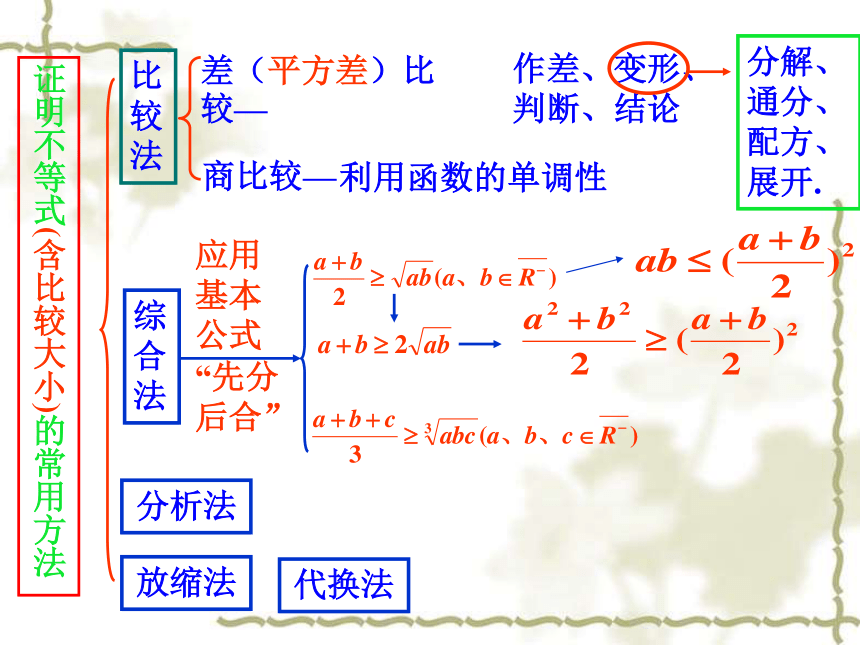
判断、结论分解、
通分、
配方、
展开.证明不等式(含比较大小)的常用方法利用函数的单调性综
合
法分析法典型例题CB对于例2，取特殊值a=1/4, b=1/2。（只能用来排除选项）例例对于例1，可用估算，或用特值法，取a=1/9。例正解：用f(1),f(- 2)来表示f(2)×例：解不等式2-3x<|2x-1|法1：不等式等价于2x-1≥02-3x<2x-1或2x-1<02-3x<1-2x法2：不等式等价于2-3x<0或2-3x≥0法3：不等式等价于 2x-1<3x-2或2x-1>2-3x分b>2；b<2； b=2三种情况例注：零点讨论法是解绝对值不等式的一般方法。(03年北京春) 若不等式|ax+2|<6的解集是(-1, 2),则实数a= .例3 解关于的不等式 证明：分析一分类讨论分析二分析、放缩法分析一平方求差法分析二分析法分析三分析：用放缩法例1.证明下列不等式
(1)若abc=1，则(2+a)(2+b)(2+c)?27;
(2)若a+b+c=1，则 ;分析二分析三（均值代换）分析一阅读下题的各种解法，指出有错误的地方配方法利用均值不等式（一正、二定、三相等）