2014年中考总复习第一轮教学案:第五讲:函数(-)直角坐标系、一次函数、反比例函数
文档属性
| 名称 | 2014年中考总复习第一轮教学案:第五讲:函数(-)直角坐标系、一次函数、反比例函数 |  | |
| 格式 | zip | ||
| 文件大小 | 422.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-02-04 16:31:40 | ||
图片预览

文档简介
2014年中考总复习第一轮:第五讲:函数(-)直角坐标系、一次函数、反比例函数
一.知识点解析:1.平面直角坐标系:⑴意义:⑵坐标平面内的点与有序实数对之间是一一对应的关系;⑶坐标平面的划分;⑷特殊点的坐标特点:①x轴上的点;②y轴上;⑸对称性:①关于x轴对称;②关于y轴对称;③关于原点对称;⑹距离公式:到①x轴距离为;②y轴距离为;③原点距离为;2.函数:⑴常量与变量;⑵函数的意义;⑶自变量的取值范围;⑷函数值;⑸函数的表示法;⑹作图像步骤;3.一次函数:⑴定义;正比例函数;⑵图像特征;⑶符号对图像的影响;⑷待定系数法求解析式;⑸两直线之间的位置关系:①必相交;②平行;③重合;④;4.反比例函数:⑴定义;⑵图像特征⑶⑷应用
二.中考中的位置、难度、分值:填空、选择、解答;中等题,6-9分;
三.失分原因:⑴题意审偏;⑵特定取值情况欠考虑,尤为与实际问题相结合;⑶计算失误;⑷分情况考虑不全
四.针对性策略:⑴认真审题;⑵在求取值范围时,要注意与实际问题相结合;⑶细心做计算;⑷要有回顾意识:有没有哪种情况还没考虑到。
五.针对性练习:
1. 如图.在直角坐标系中,矩形ABC0的边OA在x轴上,边0C在y轴上,点B的坐标为
(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴,于点E.那么点D的坐标为 。
2. 对于直角坐标平面内的任意两点A(x1,y1),B(x2,y2),定义它们之间的一种“距离”: ||AB||=|x2-x1|+|y2-y1|.给出下列三个结论: ①若点C在线段AB上,则||AC||+||CB||=||AB||;
②在△ABC中,若∠C=90°,则||AC||2+||CB||2=||AB||2;
③在△ABC中,||AC||+||C B||>||AB||.其中正确结论的个数为 。
3. 如图,在△ABC中,∠ACB=90°,AC=2,BC=1,点A、C分别在x轴、y轴上,当点A
在x轴运动时,点C随之在y轴上运动,在运动过程中,点B到原点O的最大距离为 。
4. 直线y=kx+b经过A(-1,1)和B两点,则关于x的不等式组0<kx+b<-x的解集为 。
5. 我校“心动数学”社团活动小组,在网格纸上为学校的一块空地设计植树方案如下:
第k棵树种植在点第行列处,其中,,当k≥2时,,, [a]表示非负数a的整数部分,例如[2.6]=2,[0.2]=0.按此方案,第2009棵树种植点所在的行数是4,则所在的列数是( )A.401 B.402 C.2009 D.2010
6. 如图,连接△ABC的各边中点得到一个新的△A1B1C1,又连接△A1B1C1的
各边中点得到△A2B2C2,如此无限继续下去,得到一系列三角形:△ABC,△A1B1C1,△A2B2C2,…这一系列三角形趋向于一个点M.已知A(0,0),B(3,0),C(2,2),则点M的坐标是 .
7. 在平面直角坐标系xOy中,我们把横、纵坐标都是整数的点叫做整点.已知点A(0,4),点B是x轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是 ;当点B的横坐标为4n(n为正整数)时,m= (用含n的代数式表示).
8. 阅读理解:
我们知道,任意两点关于它们所连线段的中点成中心对称,在平面直角坐标系中,任意两
点P(x1,y1)、Q(x2,y2)的对称中心的坐标为,观察应用:
(1)如图,在平面直角坐标系中,若点P1(0,-1)、P2(2,3)的对
称中心是点A,则点A的坐标为 ;
(2)另取两点B(-1.6,2.1)、C(-1,0).有一电子青蛙从点P1处开始依次关于点A、B、C
作循环对称跳动,即第一次跳到点P1关于点A的对称点P2处,接着跳到点P2关于点B的对称点P3处,第三次再跳到点P3关于点C的对称点P4处,第四次再跳到点P4关于点A的对称点P5处,…则点P3、P8的坐标分别为 .拓展延伸:(3)求出点P2012的坐标,并直接写出在x轴上与点P2012、点C构成等腰三角形的点的坐标.
9.如图,已知点A是第一象限内横坐标为2的一个定点, AC⊥x轴于点M,交直线y=﹣x
于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA, 则点P在线段ON上运动时,
A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是 .
10.如图,点P是反比例函数图象上的点,PA垂直
轴于点A(-1,0),点C的坐标为(1,0),PC交轴于点B,
连结AB,已知AB=.(1)的值是_______;(2)若
是该反比例函数图象上的点,且满足∠MBA<∠ABC,则的取值范围是______.
11.在平面直角坐标系中,点A的坐标为(1,1),点B的坐标为(11,1),
点C到直线AB的距离为4,且△ABC是直角三角形,则满足条件的点C有 个.
12. 如图,直线与双曲线()交于点.将直线向右平移
个单位后,与双曲线()交于点,与轴交于点,若,则 .
13. 如图,直线与y轴交于点A,与双曲线在第一
象限交于B、C两点,且,则k=_________.
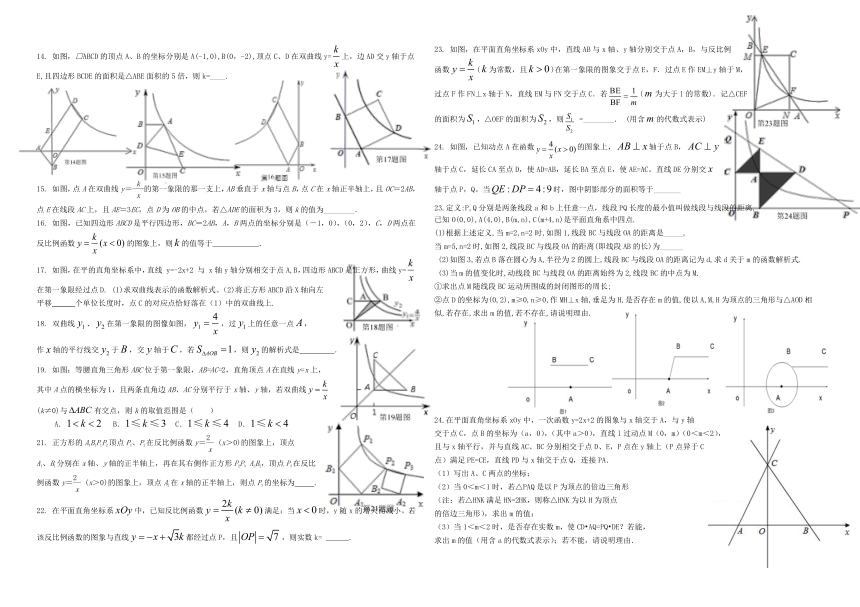
14. 如图,□ABCD的顶点A、B的坐标分别是A(-1,0),B(0,-2),顶点C、D在双曲线y=上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的5倍,则k=____.
15. 如图,点A在双曲线y=的第一象限的那一支上,AB垂直于x轴与点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为3,则k的值为________.
16. 如图,已知四边形ABCD是平行四边形,BC=2AB,A,B两点的坐标分别是(-1,0),(0,2),C,D两点在反比例函数的图象上,则的值等于 .
17. 如图,在平的直角坐标系中,直线 y=-2x+2 与 x轴y轴分别相交于点A,B,四边形ABCD是正方形,曲线y=在第一象限经过点D. (1)求双曲线表示的函数解析式。(2)将正方形ABCD沿X轴向左
平移______个单位长度时,点C的对应点恰好落在(1)中的双曲线上.
18. 双曲线、在第一象限的图像如图,,过上的任意一点,
作轴的平行线交于,交轴于,若,则的解析式是 .
19. 如图:等腰直角三角形ABC位于第一象限,AB=AC=2,直角顶点A在直线y=x上,
其中A点的横坐标为1,且两条直角边AB、AC分别平行于x轴、y轴,若双曲线
(k≠0)与有交点,则k的取值范围是( )
A. B. C. D.
21. 正方形的A1B1P1P2顶点P1、P2在反比例函数y= (x>0)的图象上,顶点
A1、B1分别在x轴、y轴的正半轴上,再在其右侧作正方形P2P3 A2B2,顶点P3在反比
例函数y= (x>0)的图象上,顶点A2在x轴的正半轴上,则点P3的坐标为 .
22. 在平面直角坐标系中,已知反比例函数满足:当时,y随x的增大而减小。若该反比例函数的图象与直线都经过点P,且,则实数k= .
23. 如图,在平面直角坐标系xOy中,直线AB与x轴、y轴分别交于点A,B,与反比例
函数(为常数,且)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,
过点F作FN⊥x轴于N,直线EM与FN交于点C.若(为大于l的常数).记△CEF
的面积为,△OEF的面积为,则 =________. (用含的代数式表示)
24. 如图,已知动点A在函数的图象上,轴于点B,
轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC。直线DE分别交
轴于点P,Q。当时,图中阴影部分的面积等于_______
23.定义:P,Q分别是两条线段a和b上任意一点,线段PQ长度的最小值叫做线段与线段的距离.
已知O(0,0),A(4,0),B(m,n),C(m+4,n)是平面直角系中四点.
根据上述定义,当m=2,n=2时,如图1,线段BC与线段OA的距离是_____,
当m=5,n=2时,如图2,线段BC与线段OA的距离(即线段AB的长)为______
(2)如图3,若点B落在圆心为A,半径为2的圆上,线段BC与线段OA的距离记为d,求d关于m的函数解析式.
(3)当m的值变化时,动线段BC与线段OA的距离始终为2,线段BC的中点为M.
①求出点M随线段BC运动所围成的封闭图形的周长;
②点D的坐标为(0,2),m≥0,n≥0,作MH⊥x轴,垂足为H,是否存在m的值,使以A,M,H为顶点的三角形与△AOD相似,若存在,求出m的值,若不存在,请说明理由.
24.在平面直角坐标系xOy中,一次函数y=2x+2的图象与x轴交于A,与y轴
交于点C,点B的坐标为(a,0),(其中a>0),直线l过动点M(0,m)(0<m<2),
且与x轴平行,并与直线AC、BC分别相交于点D、E,P点在y轴上(P点异于C
点)满足PE=CE,直线PD与x轴交于点Q,连接PA.
(1)写出A、C两点的坐标;
(2)当0<m<1时,若△PAQ是以P为顶点的倍边三角形
(注:若△HNK满足HN=2HK,则称△HNK为以H为顶点
的倍边三角形),求出m的值;
(3)当1<m<2时,是否存在实数m,使CD AQ=PQ DE?若能,
求出m的值(用含a的代数式表示);若不能,请说明理由.
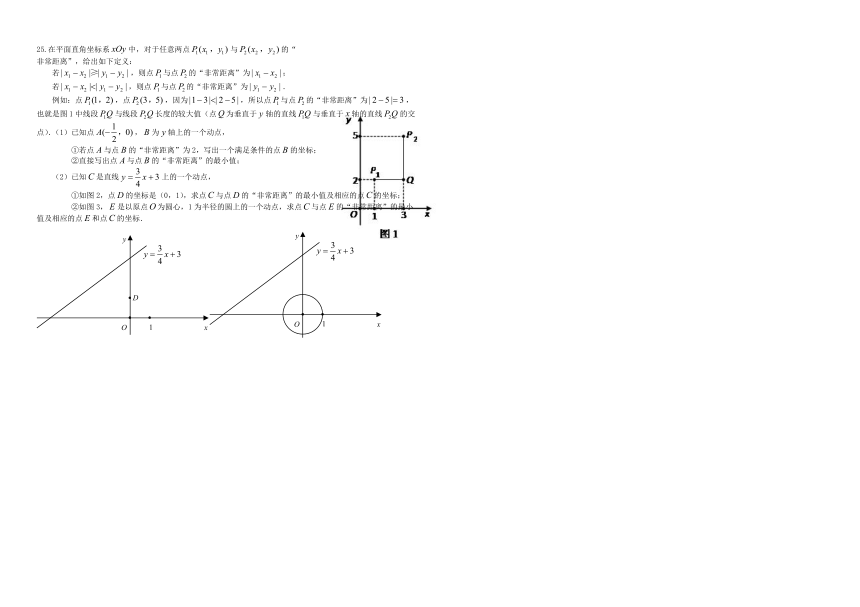
25.在平面直角坐标系中,对于任意两点与的“
非常距离”,给出如下定义:
若,则点与点的“非常距离”为;
若,则点与点的“非常距离”为.
例如:点,点,因为,所以点与点的“非常距离”为,也就是图1中线段与线段长度的较大值(点为垂直于轴的直线与垂直于轴的直线的交点).(1)已知点,为轴上的一个动点,
①若点与点的“非常距离”为2,写出一个满足条件的点的坐标;
②直接写出点与点的“非常距离”的最小值;
(2)已知是直线上的一个动点,
①如图2,点的坐标是(0,1),求点与点的“非常距离”的最小值及相应的点的坐标;
②如图3,是以原点为圆心,1为半径的圆上的一个动点,求点与点的“非常距离”的最小值及相应的点和点的坐标.
(
x
1
O
y
D
) (
x
1
O
y
)
一.知识点解析:1.平面直角坐标系:⑴意义:⑵坐标平面内的点与有序实数对之间是一一对应的关系;⑶坐标平面的划分;⑷特殊点的坐标特点:①x轴上的点;②y轴上;⑸对称性:①关于x轴对称;②关于y轴对称;③关于原点对称;⑹距离公式:到①x轴距离为;②y轴距离为;③原点距离为;2.函数:⑴常量与变量;⑵函数的意义;⑶自变量的取值范围;⑷函数值;⑸函数的表示法;⑹作图像步骤;3.一次函数:⑴定义;正比例函数;⑵图像特征;⑶符号对图像的影响;⑷待定系数法求解析式;⑸两直线之间的位置关系:①必相交;②平行;③重合;④;4.反比例函数:⑴定义;⑵图像特征⑶⑷应用
二.中考中的位置、难度、分值:填空、选择、解答;中等题,6-9分;
三.失分原因:⑴题意审偏;⑵特定取值情况欠考虑,尤为与实际问题相结合;⑶计算失误;⑷分情况考虑不全
四.针对性策略:⑴认真审题;⑵在求取值范围时,要注意与实际问题相结合;⑶细心做计算;⑷要有回顾意识:有没有哪种情况还没考虑到。
五.针对性练习:
1. 如图.在直角坐标系中,矩形ABC0的边OA在x轴上,边0C在y轴上,点B的坐标为
(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴,于点E.那么点D的坐标为 。
2. 对于直角坐标平面内的任意两点A(x1,y1),B(x2,y2),定义它们之间的一种“距离”: ||AB||=|x2-x1|+|y2-y1|.给出下列三个结论: ①若点C在线段AB上,则||AC||+||CB||=||AB||;
②在△ABC中,若∠C=90°,则||AC||2+||CB||2=||AB||2;
③在△ABC中,||AC||+||C B||>||AB||.其中正确结论的个数为 。
3. 如图,在△ABC中,∠ACB=90°,AC=2,BC=1,点A、C分别在x轴、y轴上,当点A
在x轴运动时,点C随之在y轴上运动,在运动过程中,点B到原点O的最大距离为 。
4. 直线y=kx+b经过A(-1,1)和B两点,则关于x的不等式组0<kx+b<-x的解集为 。
5. 我校“心动数学”社团活动小组,在网格纸上为学校的一块空地设计植树方案如下:
第k棵树种植在点第行列处,其中,,当k≥2时,,, [a]表示非负数a的整数部分,例如[2.6]=2,[0.2]=0.按此方案,第2009棵树种植点所在的行数是4,则所在的列数是( )A.401 B.402 C.2009 D.2010
6. 如图,连接△ABC的各边中点得到一个新的△A1B1C1,又连接△A1B1C1的
各边中点得到△A2B2C2,如此无限继续下去,得到一系列三角形:△ABC,△A1B1C1,△A2B2C2,…这一系列三角形趋向于一个点M.已知A(0,0),B(3,0),C(2,2),则点M的坐标是 .
7. 在平面直角坐标系xOy中,我们把横、纵坐标都是整数的点叫做整点.已知点A(0,4),点B是x轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是 ;当点B的横坐标为4n(n为正整数)时,m= (用含n的代数式表示).
8. 阅读理解:
我们知道,任意两点关于它们所连线段的中点成中心对称,在平面直角坐标系中,任意两
点P(x1,y1)、Q(x2,y2)的对称中心的坐标为,观察应用:
(1)如图,在平面直角坐标系中,若点P1(0,-1)、P2(2,3)的对
称中心是点A,则点A的坐标为 ;
(2)另取两点B(-1.6,2.1)、C(-1,0).有一电子青蛙从点P1处开始依次关于点A、B、C
作循环对称跳动,即第一次跳到点P1关于点A的对称点P2处,接着跳到点P2关于点B的对称点P3处,第三次再跳到点P3关于点C的对称点P4处,第四次再跳到点P4关于点A的对称点P5处,…则点P3、P8的坐标分别为 .拓展延伸:(3)求出点P2012的坐标,并直接写出在x轴上与点P2012、点C构成等腰三角形的点的坐标.
9.如图,已知点A是第一象限内横坐标为2的一个定点, AC⊥x轴于点M,交直线y=﹣x
于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA, 则点P在线段ON上运动时,
A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是 .
10.如图,点P是反比例函数图象上的点,PA垂直
轴于点A(-1,0),点C的坐标为(1,0),PC交轴于点B,
连结AB,已知AB=.(1)的值是_______;(2)若
是该反比例函数图象上的点,且满足∠MBA<∠ABC,则的取值范围是______.
11.在平面直角坐标系中,点A的坐标为(1,1),点B的坐标为(11,1),
点C到直线AB的距离为4,且△ABC是直角三角形,则满足条件的点C有 个.
12. 如图,直线与双曲线()交于点.将直线向右平移
个单位后,与双曲线()交于点,与轴交于点,若,则 .
13. 如图,直线与y轴交于点A,与双曲线在第一
象限交于B、C两点,且,则k=_________.
14. 如图,□ABCD的顶点A、B的坐标分别是A(-1,0),B(0,-2),顶点C、D在双曲线y=上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的5倍,则k=____.
15. 如图,点A在双曲线y=的第一象限的那一支上,AB垂直于x轴与点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为3,则k的值为________.
16. 如图,已知四边形ABCD是平行四边形,BC=2AB,A,B两点的坐标分别是(-1,0),(0,2),C,D两点在反比例函数的图象上,则的值等于 .
17. 如图,在平的直角坐标系中,直线 y=-2x+2 与 x轴y轴分别相交于点A,B,四边形ABCD是正方形,曲线y=在第一象限经过点D. (1)求双曲线表示的函数解析式。(2)将正方形ABCD沿X轴向左
平移______个单位长度时,点C的对应点恰好落在(1)中的双曲线上.
18. 双曲线、在第一象限的图像如图,,过上的任意一点,
作轴的平行线交于,交轴于,若,则的解析式是 .
19. 如图:等腰直角三角形ABC位于第一象限,AB=AC=2,直角顶点A在直线y=x上,
其中A点的横坐标为1,且两条直角边AB、AC分别平行于x轴、y轴,若双曲线
(k≠0)与有交点,则k的取值范围是( )
A. B. C. D.
21. 正方形的A1B1P1P2顶点P1、P2在反比例函数y= (x>0)的图象上,顶点
A1、B1分别在x轴、y轴的正半轴上,再在其右侧作正方形P2P3 A2B2,顶点P3在反比
例函数y= (x>0)的图象上,顶点A2在x轴的正半轴上,则点P3的坐标为 .
22. 在平面直角坐标系中,已知反比例函数满足:当时,y随x的增大而减小。若该反比例函数的图象与直线都经过点P,且,则实数k= .
23. 如图,在平面直角坐标系xOy中,直线AB与x轴、y轴分别交于点A,B,与反比例
函数(为常数,且)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,
过点F作FN⊥x轴于N,直线EM与FN交于点C.若(为大于l的常数).记△CEF
的面积为,△OEF的面积为,则 =________. (用含的代数式表示)
24. 如图,已知动点A在函数的图象上,轴于点B,
轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC。直线DE分别交
轴于点P,Q。当时,图中阴影部分的面积等于_______
23.定义:P,Q分别是两条线段a和b上任意一点,线段PQ长度的最小值叫做线段与线段的距离.
已知O(0,0),A(4,0),B(m,n),C(m+4,n)是平面直角系中四点.
根据上述定义,当m=2,n=2时,如图1,线段BC与线段OA的距离是_____,
当m=5,n=2时,如图2,线段BC与线段OA的距离(即线段AB的长)为______
(2)如图3,若点B落在圆心为A,半径为2的圆上,线段BC与线段OA的距离记为d,求d关于m的函数解析式.
(3)当m的值变化时,动线段BC与线段OA的距离始终为2,线段BC的中点为M.
①求出点M随线段BC运动所围成的封闭图形的周长;
②点D的坐标为(0,2),m≥0,n≥0,作MH⊥x轴,垂足为H,是否存在m的值,使以A,M,H为顶点的三角形与△AOD相似,若存在,求出m的值,若不存在,请说明理由.
24.在平面直角坐标系xOy中,一次函数y=2x+2的图象与x轴交于A,与y轴
交于点C,点B的坐标为(a,0),(其中a>0),直线l过动点M(0,m)(0<m<2),
且与x轴平行,并与直线AC、BC分别相交于点D、E,P点在y轴上(P点异于C
点)满足PE=CE,直线PD与x轴交于点Q,连接PA.
(1)写出A、C两点的坐标;
(2)当0<m<1时,若△PAQ是以P为顶点的倍边三角形
(注:若△HNK满足HN=2HK,则称△HNK为以H为顶点
的倍边三角形),求出m的值;
(3)当1<m<2时,是否存在实数m,使CD AQ=PQ DE?若能,
求出m的值(用含a的代数式表示);若不能,请说明理由.
25.在平面直角坐标系中,对于任意两点与的“
非常距离”,给出如下定义:
若,则点与点的“非常距离”为;
若,则点与点的“非常距离”为.
例如:点,点,因为,所以点与点的“非常距离”为,也就是图1中线段与线段长度的较大值(点为垂直于轴的直线与垂直于轴的直线的交点).(1)已知点,为轴上的一个动点,
①若点与点的“非常距离”为2,写出一个满足条件的点的坐标;
②直接写出点与点的“非常距离”的最小值;
(2)已知是直线上的一个动点,
①如图2,点的坐标是(0,1),求点与点的“非常距离”的最小值及相应的点的坐标;
②如图3,是以原点为圆心,1为半径的圆上的一个动点,求点与点的“非常距离”的最小值及相应的点和点的坐标.
(
x
1
O
y
D
) (
x
1
O
y
)
同课章节目录
