2014年中考总复习第一轮教学案:第六讲:二次函数
文档属性
| 名称 | 2014年中考总复习第一轮教学案:第六讲:二次函数 |  | |
| 格式 | zip | ||
| 文件大小 | 316.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-02-04 16:33:46 | ||
图片预览

文档简介
2014年中考总复习第一轮: 第六讲:二次函数
一.知识点解析:1.定义;2.二次函数的三种表示形式:⑴一般式 ⑵顶点式 ⑶交点式 ⑷待定系数法求函数解析式;3.平移问题:抓住顶点的移动是关键; 4.抛物线的图像特征:⑴开口方向 ⑵对称轴:①② ⑶顶点坐标:⑷图像的增减性; 5.符号特征:对称轴在轴左侧,同号;对称轴在轴右侧,异号;6.最值问题:要注意自变量的实际取值;7. 与方程、不等式的关系:8.与其它知识点综合:⑴与一次函数的综合:求交点坐标;求面积;求取值范围;⑵与实际生活的综合:利润、利率等;⑶与三角形、四边形的综合;⑷与圆的综合
二.中考中的位置、难度、分值:填空、选择、综合解答,中等与较难题,9-12分;
三.失分原因:①纯计算失误 ②没能与实际结合起来考虑 ③获取信息不全,导致做不下去 ④漏掉情况,少考虑一种或几种;
四.针对性策略:①计算细心认真 ②在做与实际问题综合的问题时,要清醒的看到实际的取值范围,防止最值出错;③当做不动题时,要耐心寻找信息,有的隐含的较深,通过精心分析把它找出来;④尽力量把问题考虑得周全,有再回顾意识。
五.针对性训练
1.如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过
点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若
(﹣5,y1),(,y2)是抛物线上两点,则y1>y2.其中说法正确的是( )
A ①② B ②③ C ①②④ D ②③④
2.将抛物线先向左平移2个单位,再向上平移3个单位得到抛物线 。
3.抛物线如图所示,且,则下列关系式中:
①;②;③;④正确的有 个。
4.已知二次函数的图像如图所示,关于该函数在所给自变量取值范围内,函数的最大值为,最小值为,则= 。
5.如图所示的二次函数的图像中,小兰同学得出了下面四条信息:
⑴ ⑵ ⑶ ⑷。你认为错误的是 。
6.如图所示,抛物线与双曲线的交点的横坐标是1,则关于的不等式的解集是 。
7.已知二次函数的图像与轴有两交点,则的取值范围是 。
8.已知二次函数,当自变量取时,对应的函数值大于0,当自变量分别取、时对应的函数值、,则 0(比较大小)。
9.如图,二次函数的图像与轴正半轴相交,其顶点坐标为
,下列结论① ② ③ ④
⑤,其中正确的是 (请将正确答案的序号写在横线上)。
10.若二次函数,当时,随的增大而减小,则的范围为 。
11.已知二次函数的图像经过,,当随的增大而增大时,的取值范围是 。
12.设为常数,无论为何值,二次函数的值恒为负数,则的取值范围是 。
13.如图是二次函数的图像的一部分,给出
下列命题: ① ; ②; ③的
两根分别为和1;④。其中正确的命题是 。
14.如图,一次函数的图像与二次函数图像的对称
轴交于点。⑴写出点的坐标 ;⑵已知点是二次函数
图像在轴右侧部分上的一个动点,将直线沿轴向上平移,分别
交轴、轴于、两点。若以为直角边的与相
似,则点的坐标为 。
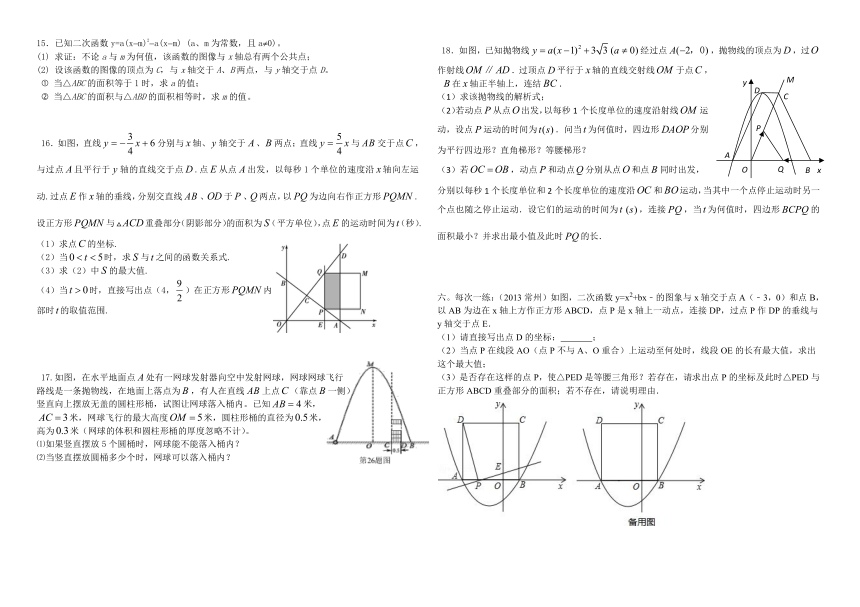
15.已知二次函数y=a(xm)2a(xm) (a、m为常数,且a0)。
(1) 求证:不论a与m为何值,该函数的图像与x轴总有两个公共点;
(2) 设该函数的图像的顶点为C,与x轴交于A、B两点,与y轴交于点D。
当△ABC的面积等于1时,求a的值;
当△ABC的面积与△ABD的面积相等时,求m的值。
16.如图,直线分别与轴、轴交于、两点;直线与交于点,与过点且平行于轴的直线交于点.点从点出发,以每秒1个单位的速度沿轴向左运动.过点作轴的垂线,分别交直线、于、两点,以为边向右作正方形.设正方形与重叠部分(阴影部分)的面积为(平方单位),点的运动时间为(秒).(1)求点的坐标.
(2)当时,求与之间的函数关系式.
(3)求(2)中的最大值.
(4)当时,直接写出点(4,)在正方形内
部时的取值范围.
17.如图,在水平地面点处有一网球发射器向空中发射网球,网球网球飞行
路线是一条抛物线,在地面上落点为,有人在直线上点(靠点一侧)
竖直向上摆放无盖的圆柱形桶,试图让网球落入桶内。已知米,
米,网球飞行的最大高度米,圆柱形桶的直径为米,
高为米(网球的体积和圆柱形桶的厚度忽略不计)。
⑴如果竖直摆放5个圆桶时,网球能不能落入桶内?
⑵当竖直摆放圆桶多少个时,网球可以落入桶内?
(
x
y
M
C
D
P
Q
O
A
B
)18.如图,已知抛物线经过点,抛物线的顶点为,过作射线.过顶点平行于轴的直线交射线于点,
在轴正半轴上,连结.
(1)求该抛物线的解析式;
(2)若动点从点出发,以每秒1个长度单位的速度沿射线运
动,设点运动的时间为.问当为何值时,四边形分别
为平行四边形?直角梯形?等腰梯形?
(3)若,动点和动点分别从点和点同时出发,
分别以每秒1个长度单位和2个长度单位的速度沿和运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为,连接,当为何值时,四边形的面积最小?并求出最小值及此时的长.
六。每次一练:(2013常州)如图,二次函数y=x2+bx﹣的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
(1)请直接写出点D的坐标: ;
(2)当点P在线段AO(点P不与A、O重合)上运动至何处时,线段OE的长有最大值,求出这个最大值;
(3)是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.
一.知识点解析:1.定义;2.二次函数的三种表示形式:⑴一般式 ⑵顶点式 ⑶交点式 ⑷待定系数法求函数解析式;3.平移问题:抓住顶点的移动是关键; 4.抛物线的图像特征:⑴开口方向 ⑵对称轴:①② ⑶顶点坐标:⑷图像的增减性; 5.符号特征:对称轴在轴左侧,同号;对称轴在轴右侧,异号;6.最值问题:要注意自变量的实际取值;7. 与方程、不等式的关系:8.与其它知识点综合:⑴与一次函数的综合:求交点坐标;求面积;求取值范围;⑵与实际生活的综合:利润、利率等;⑶与三角形、四边形的综合;⑷与圆的综合
二.中考中的位置、难度、分值:填空、选择、综合解答,中等与较难题,9-12分;
三.失分原因:①纯计算失误 ②没能与实际结合起来考虑 ③获取信息不全,导致做不下去 ④漏掉情况,少考虑一种或几种;
四.针对性策略:①计算细心认真 ②在做与实际问题综合的问题时,要清醒的看到实际的取值范围,防止最值出错;③当做不动题时,要耐心寻找信息,有的隐含的较深,通过精心分析把它找出来;④尽力量把问题考虑得周全,有再回顾意识。
五.针对性训练
1.如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过
点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若
(﹣5,y1),(,y2)是抛物线上两点,则y1>y2.其中说法正确的是( )
A ①② B ②③ C ①②④ D ②③④
2.将抛物线先向左平移2个单位,再向上平移3个单位得到抛物线 。
3.抛物线如图所示,且,则下列关系式中:
①;②;③;④正确的有 个。
4.已知二次函数的图像如图所示,关于该函数在所给自变量取值范围内,函数的最大值为,最小值为,则= 。
5.如图所示的二次函数的图像中,小兰同学得出了下面四条信息:
⑴ ⑵ ⑶ ⑷。你认为错误的是 。
6.如图所示,抛物线与双曲线的交点的横坐标是1,则关于的不等式的解集是 。
7.已知二次函数的图像与轴有两交点,则的取值范围是 。
8.已知二次函数,当自变量取时,对应的函数值大于0,当自变量分别取、时对应的函数值、,则 0(比较大小)。
9.如图,二次函数的图像与轴正半轴相交,其顶点坐标为
,下列结论① ② ③ ④
⑤,其中正确的是 (请将正确答案的序号写在横线上)。
10.若二次函数,当时,随的增大而减小,则的范围为 。
11.已知二次函数的图像经过,,当随的增大而增大时,的取值范围是 。
12.设为常数,无论为何值,二次函数的值恒为负数,则的取值范围是 。
13.如图是二次函数的图像的一部分,给出
下列命题: ① ; ②; ③的
两根分别为和1;④。其中正确的命题是 。
14.如图,一次函数的图像与二次函数图像的对称
轴交于点。⑴写出点的坐标 ;⑵已知点是二次函数
图像在轴右侧部分上的一个动点,将直线沿轴向上平移,分别
交轴、轴于、两点。若以为直角边的与相
似,则点的坐标为 。
15.已知二次函数y=a(xm)2a(xm) (a、m为常数,且a0)。
(1) 求证:不论a与m为何值,该函数的图像与x轴总有两个公共点;
(2) 设该函数的图像的顶点为C,与x轴交于A、B两点,与y轴交于点D。
当△ABC的面积等于1时,求a的值;
当△ABC的面积与△ABD的面积相等时,求m的值。
16.如图,直线分别与轴、轴交于、两点;直线与交于点,与过点且平行于轴的直线交于点.点从点出发,以每秒1个单位的速度沿轴向左运动.过点作轴的垂线,分别交直线、于、两点,以为边向右作正方形.设正方形与重叠部分(阴影部分)的面积为(平方单位),点的运动时间为(秒).(1)求点的坐标.
(2)当时,求与之间的函数关系式.
(3)求(2)中的最大值.
(4)当时,直接写出点(4,)在正方形内
部时的取值范围.
17.如图,在水平地面点处有一网球发射器向空中发射网球,网球网球飞行
路线是一条抛物线,在地面上落点为,有人在直线上点(靠点一侧)
竖直向上摆放无盖的圆柱形桶,试图让网球落入桶内。已知米,
米,网球飞行的最大高度米,圆柱形桶的直径为米,
高为米(网球的体积和圆柱形桶的厚度忽略不计)。
⑴如果竖直摆放5个圆桶时,网球能不能落入桶内?
⑵当竖直摆放圆桶多少个时,网球可以落入桶内?
(
x
y
M
C
D
P
Q
O
A
B
)18.如图,已知抛物线经过点,抛物线的顶点为,过作射线.过顶点平行于轴的直线交射线于点,
在轴正半轴上,连结.
(1)求该抛物线的解析式;
(2)若动点从点出发,以每秒1个长度单位的速度沿射线运
动,设点运动的时间为.问当为何值时,四边形分别
为平行四边形?直角梯形?等腰梯形?
(3)若,动点和动点分别从点和点同时出发,
分别以每秒1个长度单位和2个长度单位的速度沿和运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为,连接,当为何值时,四边形的面积最小?并求出最小值及此时的长.
六。每次一练:(2013常州)如图,二次函数y=x2+bx﹣的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
(1)请直接写出点D的坐标: ;
(2)当点P在线段AO(点P不与A、O重合)上运动至何处时,线段OE的长有最大值,求出这个最大值;
(3)是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.
同课章节目录
