2014年中考总复习第一轮教学案:第八讲:四边形
文档属性
| 名称 | 2014年中考总复习第一轮教学案:第八讲:四边形 |
|
|
| 格式 | zip | ||
| 文件大小 | 235.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-02-04 00:00:00 | ||
图片预览

文档简介
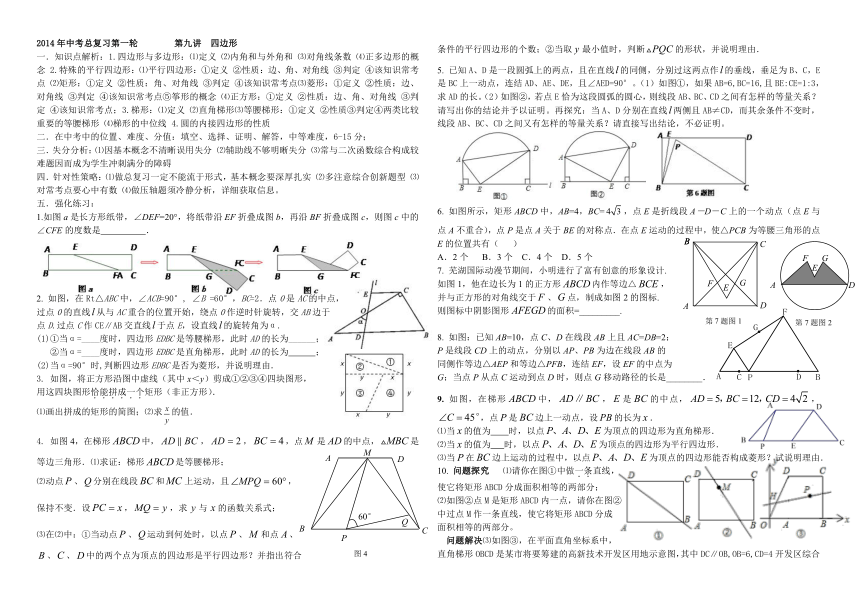
2014年中考总复习第一轮 第九讲 四边形
一.知识点解析:1.四边形与多边形:⑴定义 ⑵内角和与外角和 ⑶对角线条数 ⑷正多边形的概念 2.特殊的平行四边形:⑴平行四边形:①定义 ②性质:边、角、对角线 ③判定 ④该知识常考点 ⑵矩形:①定义 ②性质:角、对角线 ③判定 ④该知识常考点⑶菱形:①定义 ②性质:边、对角线 ③判定 ④该知识常考点⑤筝形的概念 ⑷正方形:①定义 ②性质:边、角、对角线 ③判定 ④该知识常考点;3.梯形:⑴定义 ⑵直角梯形⑶等腰梯形:①定义 ②性质③判定④两类比较重要的等腰梯形 ⑷梯形的中位线 4.圆的内接四边形的性质
二.在中考中的位置、难度、分值:填空、选择、证明、解答,中等难度,6-15分;
三.失分分析:⑴因基本概念不清晰误用失分 ⑵辅助线不够明晰失分 ⑶常与二次函数综合构成较难题因而成为学生冲刺满分的障碍
四.针对性策略:⑴做总复习一定不能流于形式,基本概念要深厚扎实 ⑵多注意综合创新题型 ⑶对常考点要心中有数 ⑷做压轴题须冷静分析,详细获取信息。
五.强化练习:
1.如图a是长方形纸带,∠DEF=20°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是 .
2. 如图,在Rt△ABC中,∠ACB=90°, ∠B =60°,BC=2.点0是AC的中点,
过点0的直线从与AC重合的位置开始,绕点0作逆时针旋转,交AB边于
点D.过点C作CE∥AB交直线于点E,设直线的旋转角为α.
(1)①当α=____度时,四边形EDBC是等腰梯形,此时AD的长为______;
②当α=____度时,四边形EDBC是直角梯形,此时AD的长为 ;
(2)当α=90°时,判断四边形EDBC是否为菱形,并说明理由.
3. 如图,将正方形沿图中虚线(其中x<y)剪成①②③④四块图形,
用这四块图形恰能拼成一个矩形(非正方形).
⑴画出拼成的矩形的简图;⑵求的值.
(
A
D
C
B
P
M
Q
60
°
图
4
)4. 如图4,在梯形中,,,,点是的中点,是等边三角形.⑴求证:梯形是等腰梯形;
⑵动点、分别在线段和上运动,且,
保持不变.设,,求与的函数关系式;
⑶在⑵中:①当动点、运动到何处时,以点、和点、
、、中的两个点为顶点的四边形是平行四边形?并指出符合
条件的平行四边形的个数;②当取最小值时,判断的形状,并说明理由.
5. 已知A、D是一段圆弧上的两点,且在直线的同侧,分别过这两点作的垂线,垂足为B、C,E是BC上一动点,连结AD、AE、DE,且∠AED=90°。(1)如图①,如果AB=6,BC=16,且BE:CE=1:3,求AD的长。(2)如图②,若点E恰为这段圆弧的圆心,则线段AB、BC、CD之间有怎样的等量关系?请写出你的结论并予以证明。再探究:当A、D分别在直线两侧且AB≠CD,而其余条件不变时,线段AB、BC、CD之间又有怎样的等量关系?请直接写出结论,不必证明。
(
C
D
B
A
F
E
G
第
7
题图
1
第
7
题图
2
E
F
G
A
B
D
)6. 如图所示,矩形ABCD中,AB=4,BC=,点E是折线段A-D-C上的一个动点(点E与点A不重合),点P是点A关于BE的对称点.在点E运动的过程中,使△PCB为等腰三角形的点E的位置共有( )
A.2个 B.3个 C.4个 D.5个
7. 芜湖国际动漫节期间,小明进行了富有创意的形象设计.
如图1,他在边长为1的正方形内作等边△,
并与正方形的对角线交于、点,制成如图2的图标.
则图标中阴影图形的面积=_________.
8. 如图:已知AB=10,点C、D在线段AB上且AC=DB=2;
P是线段CD上的动点,分别以AP、PB为边在线段AB的
同侧作等边△AEP和等边△PFB,连结EF,设EF的中点为
G;当点P从点C运动到点D时,则点G移动路径的长是________.
9. 如图,在梯形中,,是的中点,,,点是边上一动点,设的长为.
⑴当的值为 时,以点为顶点的四边形为直角梯形.
⑵当的值为 时,以点为顶点的四边形为平行四边形.
⑶当在边上运动的过程中,以点为顶点的四边形能否构成菱形?试说明理由.
10. 问题探究 ⑴请你在图①中做一条直线,
使它将矩形ABCD分成面积相等的两部分;
⑵如图②点M是矩形ABCD内一点,请你在图②
中过点M作一条直线,使它将矩形ABCD分成
面积相等的两部分。
问题解决⑶如图③,在平面直角坐标系中,
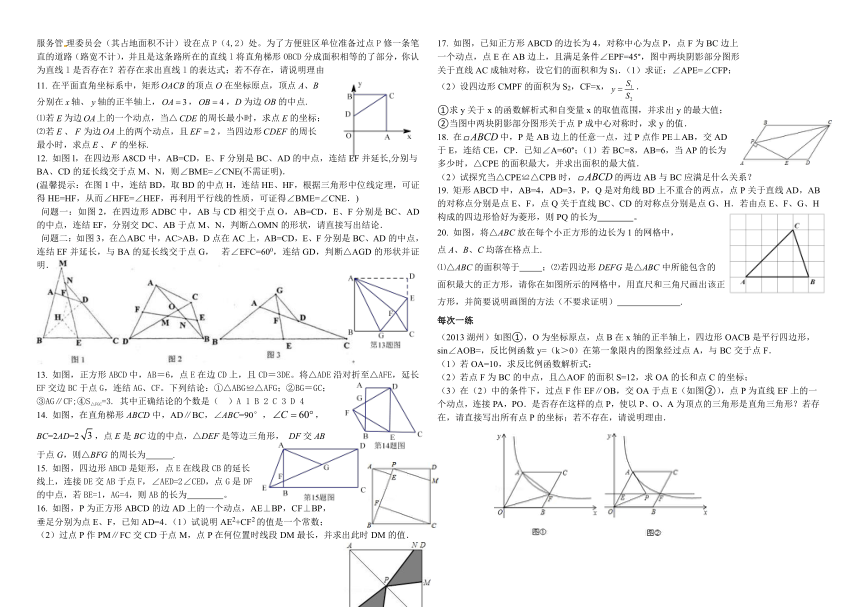
直角梯形OBCD是某市将要筹建的高新技术开发区用地示意图,其中DC∥OB,OB=6,CD=4开发区综合服务管理委员会(其占地面积不计)设在点P(4,2)处。为了方便驻区单位准备过点P修一条笔直的道路(路宽不计),并且是这条路所在的直线l将直角梯形OBCD分成面积相等的了部分,你认为直线l是否存在?若存在求出直线l的表达式;若不存在,请说明理由
11. 在平面直角坐标系中,矩形的顶点O在坐标原点,顶点A、B
分别在轴、轴的正半轴上,,,D为边OB的中点.
⑴若为边上的一个动点,当△的周长最小时,求点的坐标;
⑵若、为边上的两个动点,且,当四边形的周长
最小时,求点、的坐标.
12. 如图l,在四边形A8CD中,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE(不需证明).
(温馨提示:在图1中,连结BD,取BD的中点H,连结HE、HF,根据三角形中位线定理,可证得HE=HF,从而∠HFE=∠HEF,再利用平行线的性质,可证得∠BME=∠CNE.)
问题一:如图2,在四边形ADBC中,AB与CD相交于点O,AB=CD,E、F分别是BC、AD的中点,连结EF,分别交DC、AB于点M、N,判断△OMN的形状,请直接写出结论.
问题二:如图3,在△ABC中,AC>AB,D点在AC上,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,与BA的延长线交于点G, 若∠EFC=600,连结GD,判断△AGD的形状并证明.
13. 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE。将△ADE沿对折至△AFE,延长EF交边BC于点G,连结AG、CF。下列结论:①△ABG≌△AFG;②BG=GC;
③AG∥CF;④S△FGC=3. 其中正确结论的个数是( )A 1 B 2 C 3 D 4
14. 如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,,
BC=2AD=2,点E是BC边的中点,△DEF是等边三角形, DF交AB
于点G,则△BFG的周长为 .
15. 如图,四边形ABCD是矩形,点E在线段CB的延长
线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF
的中点,若BE=1,AG=4,则AB的长为 。
16. 如图,P为正方形ABCD的边AD上的一个动点,AE⊥BP,CF⊥BP,
垂足分别为点E、F,已知AD=4.(1)试说明AE2+CF2的值是一个常数;
(2)过点P作PM∥FC交CD于点M,点P在何位置时线段DM最长,并求出此时DM的值.
17. 如图,已知正方形ABCD的边长为4,对称中心为点P,点F为BC边上
一个动点,点E在AB边上,且满足条件∠EPF=45°,图中两块阴影部分图形
关于直线AC成轴对称,设它们的面积和为S1.(1)求证:∠APE=∠CFP;
(2)设四边形CMPF的面积为S2,CF=x,.
①求y关于x的函数解析式和自变量x的取值范围,并求出y的最大值;
②当图中两块阴影部分图形关于点P成中心对称时,求y的值.
18. 在中,P是AB边上的任意一点,过P点作PE⊥AB,交AD
于E,连结CE,CP.已知∠A=60°;(1)若BC=8,AB=6,当AP的长为
多少时,△CPE的面积最大,并求出面积的最大值.
(2)试探究当△CPE≌△CPB时,的两边AB与BC应满足什么关系?
19. 矩形ABCD中,AB=4,AD=3,P,Q是对角线BD上不重合的两点,点P关于直线AD,AB的对称点分别是点E、F,点Q关于直线BC、CD的对称点分别是点G、H.若由点E、F、G、H构成的四边形恰好为菱形,则PQ的长为 。
20. 如图,将△ABC放在每个小正方形的边长为1的网格中,
点A、B、C均落在格点上.
⑴△ABC的面积等于 ;⑵若四边形DEFG是△ABC中所能包含的
面积最大的正方形,请你在如图所示的网格中,用直尺和三角尺画出该正
方形,并简要说明画图的方法(不要求证明) .
每次一练
(2013湖州)如图①,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,sin∠AOB=,反比例函数y=(k>0)在第一象限内的图象经过点A,与BC交于点F.
(1)若OA=10,求反比例函数解析式;
(2)若点F为BC的中点,且△AOF的面积S=12,求OA的长和点C的坐标;
(3)在(2)中的条件下,过点F作EF∥OB,交OA于点E(如图②),点P为直线EF上的一个动点,连接PA,PO.是否存在这样的点P,使以P、O、A为顶点的三角形是直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
一.知识点解析:1.四边形与多边形:⑴定义 ⑵内角和与外角和 ⑶对角线条数 ⑷正多边形的概念 2.特殊的平行四边形:⑴平行四边形:①定义 ②性质:边、角、对角线 ③判定 ④该知识常考点 ⑵矩形:①定义 ②性质:角、对角线 ③判定 ④该知识常考点⑶菱形:①定义 ②性质:边、对角线 ③判定 ④该知识常考点⑤筝形的概念 ⑷正方形:①定义 ②性质:边、角、对角线 ③判定 ④该知识常考点;3.梯形:⑴定义 ⑵直角梯形⑶等腰梯形:①定义 ②性质③判定④两类比较重要的等腰梯形 ⑷梯形的中位线 4.圆的内接四边形的性质
二.在中考中的位置、难度、分值:填空、选择、证明、解答,中等难度,6-15分;
三.失分分析:⑴因基本概念不清晰误用失分 ⑵辅助线不够明晰失分 ⑶常与二次函数综合构成较难题因而成为学生冲刺满分的障碍
四.针对性策略:⑴做总复习一定不能流于形式,基本概念要深厚扎实 ⑵多注意综合创新题型 ⑶对常考点要心中有数 ⑷做压轴题须冷静分析,详细获取信息。
五.强化练习:
1.如图a是长方形纸带,∠DEF=20°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是 .
2. 如图,在Rt△ABC中,∠ACB=90°, ∠B =60°,BC=2.点0是AC的中点,
过点0的直线从与AC重合的位置开始,绕点0作逆时针旋转,交AB边于
点D.过点C作CE∥AB交直线于点E,设直线的旋转角为α.
(1)①当α=____度时,四边形EDBC是等腰梯形,此时AD的长为______;
②当α=____度时,四边形EDBC是直角梯形,此时AD的长为 ;
(2)当α=90°时,判断四边形EDBC是否为菱形,并说明理由.
3. 如图,将正方形沿图中虚线(其中x<y)剪成①②③④四块图形,
用这四块图形恰能拼成一个矩形(非正方形).
⑴画出拼成的矩形的简图;⑵求的值.
(
A
D
C
B
P
M
Q
60
°
图
4
)4. 如图4,在梯形中,,,,点是的中点,是等边三角形.⑴求证:梯形是等腰梯形;
⑵动点、分别在线段和上运动,且,
保持不变.设,,求与的函数关系式;
⑶在⑵中:①当动点、运动到何处时,以点、和点、
、、中的两个点为顶点的四边形是平行四边形?并指出符合
条件的平行四边形的个数;②当取最小值时,判断的形状,并说明理由.
5. 已知A、D是一段圆弧上的两点,且在直线的同侧,分别过这两点作的垂线,垂足为B、C,E是BC上一动点,连结AD、AE、DE,且∠AED=90°。(1)如图①,如果AB=6,BC=16,且BE:CE=1:3,求AD的长。(2)如图②,若点E恰为这段圆弧的圆心,则线段AB、BC、CD之间有怎样的等量关系?请写出你的结论并予以证明。再探究:当A、D分别在直线两侧且AB≠CD,而其余条件不变时,线段AB、BC、CD之间又有怎样的等量关系?请直接写出结论,不必证明。
(
C
D
B
A
F
E
G
第
7
题图
1
第
7
题图
2
E
F
G
A
B
D
)6. 如图所示,矩形ABCD中,AB=4,BC=,点E是折线段A-D-C上的一个动点(点E与点A不重合),点P是点A关于BE的对称点.在点E运动的过程中,使△PCB为等腰三角形的点E的位置共有( )
A.2个 B.3个 C.4个 D.5个
7. 芜湖国际动漫节期间,小明进行了富有创意的形象设计.
如图1,他在边长为1的正方形内作等边△,
并与正方形的对角线交于、点,制成如图2的图标.
则图标中阴影图形的面积=_________.
8. 如图:已知AB=10,点C、D在线段AB上且AC=DB=2;
P是线段CD上的动点,分别以AP、PB为边在线段AB的
同侧作等边△AEP和等边△PFB,连结EF,设EF的中点为
G;当点P从点C运动到点D时,则点G移动路径的长是________.
9. 如图,在梯形中,,是的中点,,,点是边上一动点,设的长为.
⑴当的值为 时,以点为顶点的四边形为直角梯形.
⑵当的值为 时,以点为顶点的四边形为平行四边形.
⑶当在边上运动的过程中,以点为顶点的四边形能否构成菱形?试说明理由.
10. 问题探究 ⑴请你在图①中做一条直线,
使它将矩形ABCD分成面积相等的两部分;
⑵如图②点M是矩形ABCD内一点,请你在图②
中过点M作一条直线,使它将矩形ABCD分成
面积相等的两部分。
问题解决⑶如图③,在平面直角坐标系中,
直角梯形OBCD是某市将要筹建的高新技术开发区用地示意图,其中DC∥OB,OB=6,CD=4开发区综合服务管理委员会(其占地面积不计)设在点P(4,2)处。为了方便驻区单位准备过点P修一条笔直的道路(路宽不计),并且是这条路所在的直线l将直角梯形OBCD分成面积相等的了部分,你认为直线l是否存在?若存在求出直线l的表达式;若不存在,请说明理由
11. 在平面直角坐标系中,矩形的顶点O在坐标原点,顶点A、B
分别在轴、轴的正半轴上,,,D为边OB的中点.
⑴若为边上的一个动点,当△的周长最小时,求点的坐标;
⑵若、为边上的两个动点,且,当四边形的周长
最小时,求点、的坐标.
12. 如图l,在四边形A8CD中,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE(不需证明).
(温馨提示:在图1中,连结BD,取BD的中点H,连结HE、HF,根据三角形中位线定理,可证得HE=HF,从而∠HFE=∠HEF,再利用平行线的性质,可证得∠BME=∠CNE.)
问题一:如图2,在四边形ADBC中,AB与CD相交于点O,AB=CD,E、F分别是BC、AD的中点,连结EF,分别交DC、AB于点M、N,判断△OMN的形状,请直接写出结论.
问题二:如图3,在△ABC中,AC>AB,D点在AC上,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,与BA的延长线交于点G, 若∠EFC=600,连结GD,判断△AGD的形状并证明.
13. 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE。将△ADE沿对折至△AFE,延长EF交边BC于点G,连结AG、CF。下列结论:①△ABG≌△AFG;②BG=GC;
③AG∥CF;④S△FGC=3. 其中正确结论的个数是( )A 1 B 2 C 3 D 4
14. 如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,,
BC=2AD=2,点E是BC边的中点,△DEF是等边三角形, DF交AB
于点G,则△BFG的周长为 .
15. 如图,四边形ABCD是矩形,点E在线段CB的延长
线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF
的中点,若BE=1,AG=4,则AB的长为 。
16. 如图,P为正方形ABCD的边AD上的一个动点,AE⊥BP,CF⊥BP,
垂足分别为点E、F,已知AD=4.(1)试说明AE2+CF2的值是一个常数;
(2)过点P作PM∥FC交CD于点M,点P在何位置时线段DM最长,并求出此时DM的值.
17. 如图,已知正方形ABCD的边长为4,对称中心为点P,点F为BC边上
一个动点,点E在AB边上,且满足条件∠EPF=45°,图中两块阴影部分图形
关于直线AC成轴对称,设它们的面积和为S1.(1)求证:∠APE=∠CFP;
(2)设四边形CMPF的面积为S2,CF=x,.
①求y关于x的函数解析式和自变量x的取值范围,并求出y的最大值;
②当图中两块阴影部分图形关于点P成中心对称时,求y的值.
18. 在中,P是AB边上的任意一点,过P点作PE⊥AB,交AD
于E,连结CE,CP.已知∠A=60°;(1)若BC=8,AB=6,当AP的长为
多少时,△CPE的面积最大,并求出面积的最大值.
(2)试探究当△CPE≌△CPB时,的两边AB与BC应满足什么关系?
19. 矩形ABCD中,AB=4,AD=3,P,Q是对角线BD上不重合的两点,点P关于直线AD,AB的对称点分别是点E、F,点Q关于直线BC、CD的对称点分别是点G、H.若由点E、F、G、H构成的四边形恰好为菱形,则PQ的长为 。
20. 如图,将△ABC放在每个小正方形的边长为1的网格中,
点A、B、C均落在格点上.
⑴△ABC的面积等于 ;⑵若四边形DEFG是△ABC中所能包含的
面积最大的正方形,请你在如图所示的网格中,用直尺和三角尺画出该正
方形,并简要说明画图的方法(不要求证明) .
每次一练
(2013湖州)如图①,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,sin∠AOB=,反比例函数y=(k>0)在第一象限内的图象经过点A,与BC交于点F.
(1)若OA=10,求反比例函数解析式;
(2)若点F为BC的中点,且△AOF的面积S=12,求OA的长和点C的坐标;
(3)在(2)中的条件下,过点F作EF∥OB,交OA于点E(如图②),点P为直线EF上的一个动点,连接PA,PO.是否存在这样的点P,使以P、O、A为顶点的三角形是直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
同课章节目录
