2014年中考总复习第一轮教学案:第九讲:全等与相似
文档属性
| 名称 | 2014年中考总复习第一轮教学案:第九讲:全等与相似 |  | |
| 格式 | zip | ||
| 文件大小 | 277.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-02-04 16:41:04 | ||
图片预览

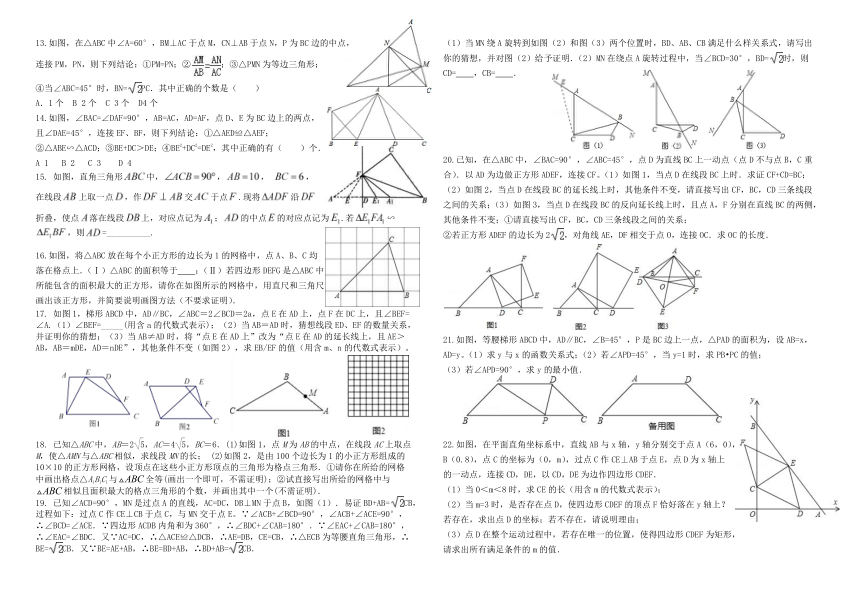
文档简介
2014年中考总复习第一轮: 第九讲:全等与相似
一.知识点精析:
1.全等三角形:⑴定义;⑵全等三角形的性质:①②③④⑤;⑶全等三角形的判定:、、、;⑷的判定:、、、、;
2.比例:⑴定义;⑵比例中项,黄金分割,第四比例项;⑶比例的基本性质;⑷重要性质:合分比性质、等比性质。
3.相似三角形:⑴平行线分线段成比例定理;⑵定义;⑶相似三角形的性质:①②③④⑤;⑷相似三角形的判定:①②③;⑸相似的两个基本图形:形图、形图。
4.射影定理:在中,,,则①;
②;③;
二.本知识点在中考中的位置作用:全等与相似在中考中起着极为重要的工具作用,利用相似(或全等)是我们首先想到的处理方法。
三.中考中常见的辅助线作法:⑴中点问题:①倍延中线;②中位线;③直角三角形斜边中线等于斜边一半;⑵二倍角问题;⑶一条线段等于两条线段之和:截长补短;⑷等腰三角形:三线合一;⑸垂直平分线;⑹角平分线;⑺直角三角形:斜边中线等于斜边一半;⑻等腰三角形、角平分线、平行线;⑼关于折叠问题;⑽关于“小河”问题。
四.典型题强化
1. 如图,在ABC内有边长分别为的三个正方形,则满足
的关系式是( )A、 B、 C、 D、
2. 如图,点A1,A2,A3,A4在射线OA上,点B1,B2,B3在射线OB上,
且A1B1∥A2B2∥A3B3,A2B1∥A3B2∥A4B3.若△A2B1B2,△A3B2B3的面积分
别为1,4,则图中三个阴影三角形面积之和为____________.
3.如图,在△ABC中,AB=AC=a,BC=b(a>b).在△ABC内依次作
(
(第
4
题)
A
B
C
F
E
P
H
)∠CBD=∠A,∠DCE=∠CBD,∠EDF=∠DCE.则EF等于( )
4. 如图,在等腰中,是底边上的高线,点
是线段上不与端点重合的任意一点,连接交于点,连接交
于点.(1)证明:;(2)证明:;
(3)以线段和为边构成一个新的三角形(点与点重合于点),记和的面积分别为和,如果存在点,能使得,求的取值范围.
5. 如图,矩形ABCD中,由8个面积均为1的小正方形组成的L型模板
如图放置,则矩形ABCD的周长为 _.
6. 如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=α,
且DM交AC于F,ME交BC于G.
(1)写出图中三对相似三角形,并证明其中的一对;
(2)连结FG,如果α=45°,AB=,AF=3,求FG的长.
(
D
C
B
E
A
H
)7. 在直角梯形中,,为
边上一点,,且.连接交对角线于,
(
A
D
C
E
B
(第
8
题)
)连接.下列结论:①;②为等边三角形;
③; ④.其中结论正确的是( )
A.只有①② B.只有①②④ C.只有③④ D.①②③④
8. 如图,等腰△ABC中,底边,,的平分线交AC
于D,的平=线交BD于E,设,则( )
A. B. C. D.
9. 如图矩形纸片ABCD,AB=5cm,BC=10cm,CD上有一点E,ED=2cm,
AD上有一点P,PD=3cm,过P作PF⊥AD交BC于F,将纸片折叠,使P
点与E点重合,折痕与PF交于Q点,则PQ的长是________cm.
(
A
1
B
1
C
1
C
A
B
a
b
c
c
1
b
1
a
1
第
10
题图
)10. 如图,已知,相似比为k(k>1),且的三边长分别为a、b、c(a>b>c),的三边长分别为、、.
(1)若c=a1,求证:a=kc;(2)若c=a1,试给出符合条件
的一对和,使得a、b、c和、、都是
正整数,并加以说明;(3)若b=a1,c=b1,是否存在和使得k=2?请说明理由.
11. 如图,在平面直角坐标系中,点是坐标原点,四边形是梯形,,点的坐标为,点的坐标为,.(1)求点的坐标;
(2)点从点出发,沿线段以个单位/秒的速度向终点匀速运动,过点作,垂足为,设的面积为,点的运动时间为秒,求与之间的函数关系式(直接写出自变量的取值范围);
(
(第
11
题图)
(
第
11
题备用
图)
)(3)在(2)的条件下,过点作交线段于点,过点作,垂足为,线段分别交直线于点,点为线段的中点,连接.当为何值时,?
12. 在三角形纸片ABC中,已知∠ABC=90°,AB=6,BC=8。过点A作直线平行于BC,折叠三角形纸片ABC,使直角顶点B落在直线上的T处,折痕为MN.当点T在直线上移动时,折痕的端点M、N也随之移动.若限定端点M、N分别在AB、BC边上移动,则线段AT长度的最大值与最小值之和为_________ (计算结果不取近似值).
13.如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,
连接PM,PN,则下列结论:①PM=PN;②;③△PMN为等边三角形;
④当∠ABC=45°时,BN=PC.其中正确的个数是( )
A.1个 B 2个 C 3个 D4个
14.如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,
且∠DAE=45°,连接EF、BF,则下列结论:①△AED≌△AEF;
②△ABE∽△ACD;③BE+DC>DE;④BE2+DC2=DE2,其中正确的有( )个.
A 1 B 2 C 3 D 4
15. 如图,直角三角形中,,, ,
在线段上取一点,作交于点.现将沿
折叠,使点落在线段上,对应点记为;的中点的对应点记为.若∽,则=__________.
16.如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均
落在格点上.(Ⅰ)△ABC的面积等于 ;(Ⅱ)若四边形DEFG是△ABC中
所能包含的面积最大的正方形,请你在如图所示的网格中,用直尺和三角尺
画出该正方形,并简要说明画图方法(不要求证明).
17. 如图1,梯形ABCD中,AD∥BC,∠ABC=2∠BCD=2a,点E在AD上,点F在DC上,且∠BEF=∠A.(1)∠BEF=_____(用含a的代数式表示);(2)当AB=AD时,猜想线段ED、EF的数量关系,并证明你的猜想;(3)当AB≠AD时,将“点E在AD上”改为“点E在AD的延长线上,且AE>AB,AB=mDE,AD=nDE”,其他条件不变(如图2),求EB/EF的值(用含m、n的代数式表示)。
18. 已知△ABC中,AB=2,AC=4,BC=6.(1)如图1,点M为AB的中点,在线段AC上取点M,使△AMN与△ABC相似,求线段MN的长; (2)如图2,是由100个边长为1的小正方形组成的10×10的正方形网格,设顶点在这些小正方形顶点的三角形为格点三角形.①请你在所给的网格中画出格点△A1B1C1与全等(画出一个即可,不需证明);②试直接写出所给的网格中与相似且面积最大的格点三角形的个数,并画出其中一个(不需证明).
19. 已知∠ACD=90°,MN是过点A的直线,AC=DC,DB⊥MN于点B,如图(1).易证BD+AB=CB,过程如下:过点C作CE⊥CB于点C,与MN交于点E。∵∠ACB+∠BCD=90°,∠ACB+∠ACE=90°,∴∠BCD=∠ACE.∵四边形ACDB内角和为360°,∴∠BDC+∠CAB=180°.∵∠EAC+∠CAB=180°,∴∠EAC=∠BDC.又∵AC=DC,∴△ACE≌△DCB,∴AE=DB,CE=CB,∴△ECB为等腰直角三角形,∴BE=CB.又∵BE=AE+AB,∴BE=BD+AB,∴BD+AB=CB.
(1)当MN绕A旋转到如图(2)和图(3)两个位置时,BD、AB、CB满足什么样关系式,请写出你的猜想,并对图(2)给予证明.(2)MN在绕点A旋转过程中,当∠BCD=30°,BD=时,则CD= ,CB= .
20.已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与点B,C重合).以AD为边做正方形ADEF,连接CF。(1)如图1,当点D在线段BC上时.求证CF+CD=BC;
(2)如图2,当点D在线段BC的延长线上时,其他条件不变,请直接写出CF,BC,CD三条线段之间的关系;(3)如图3,当点D在线段BC的反向延长线上时,且点A,F分别在直线BC的两侧,其他条件不变;①请直接写出CF,BC,CD三条线段之间的关系;
②若正方形ADEF的边长为2,对角线AE,DF相交于点O,连接OC.求OC的长度.
21.如图,等腰梯形ABCD中,AD∥BC,∠B=45°,P是BC边上一点,△PAD的面积为,设AB=x,AD=y。(1)求y与x的函数关系式;(2)若∠APD=45°,当y=1时,求PB PC的值;
(3)若∠APD=90°,求y的最小值.
22.如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(6,0),
B(0.8),点C的坐标为(0,m),过点C作CE⊥AB于点E,点D为x轴上
的一动点,连接CD,DE,以CD,DE为边作四边形CDEF.
(1)当0<m<8时,求CE的长(用含m的代数式表示);
(2)当m=3时,是否存在点D,使四边形CDEF的顶点F恰好落在y轴上?
若存在,求出点D的坐标;若不存在,请说明理由;
(3)点D在整个运动过程中,若存在唯一的位置,使得四边形CDEF为矩形,
请求出所有满足条件的m的值.
一.知识点精析:
1.全等三角形:⑴定义;⑵全等三角形的性质:①②③④⑤;⑶全等三角形的判定:、、、;⑷的判定:、、、、;
2.比例:⑴定义;⑵比例中项,黄金分割,第四比例项;⑶比例的基本性质;⑷重要性质:合分比性质、等比性质。
3.相似三角形:⑴平行线分线段成比例定理;⑵定义;⑶相似三角形的性质:①②③④⑤;⑷相似三角形的判定:①②③;⑸相似的两个基本图形:形图、形图。
4.射影定理:在中,,,则①;
②;③;
二.本知识点在中考中的位置作用:全等与相似在中考中起着极为重要的工具作用,利用相似(或全等)是我们首先想到的处理方法。
三.中考中常见的辅助线作法:⑴中点问题:①倍延中线;②中位线;③直角三角形斜边中线等于斜边一半;⑵二倍角问题;⑶一条线段等于两条线段之和:截长补短;⑷等腰三角形:三线合一;⑸垂直平分线;⑹角平分线;⑺直角三角形:斜边中线等于斜边一半;⑻等腰三角形、角平分线、平行线;⑼关于折叠问题;⑽关于“小河”问题。
四.典型题强化
1. 如图,在ABC内有边长分别为的三个正方形,则满足
的关系式是( )A、 B、 C、 D、
2. 如图,点A1,A2,A3,A4在射线OA上,点B1,B2,B3在射线OB上,
且A1B1∥A2B2∥A3B3,A2B1∥A3B2∥A4B3.若△A2B1B2,△A3B2B3的面积分
别为1,4,则图中三个阴影三角形面积之和为____________.
3.如图,在△ABC中,AB=AC=a,BC=b(a>b).在△ABC内依次作
(
(第
4
题)
A
B
C
F
E
P
H
)∠CBD=∠A,∠DCE=∠CBD,∠EDF=∠DCE.则EF等于( )
4. 如图,在等腰中,是底边上的高线,点
是线段上不与端点重合的任意一点,连接交于点,连接交
于点.(1)证明:;(2)证明:;
(3)以线段和为边构成一个新的三角形(点与点重合于点),记和的面积分别为和,如果存在点,能使得,求的取值范围.
5. 如图,矩形ABCD中,由8个面积均为1的小正方形组成的L型模板
如图放置,则矩形ABCD的周长为 _.
6. 如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=α,
且DM交AC于F,ME交BC于G.
(1)写出图中三对相似三角形,并证明其中的一对;
(2)连结FG,如果α=45°,AB=,AF=3,求FG的长.
(
D
C
B
E
A
H
)7. 在直角梯形中,,为
边上一点,,且.连接交对角线于,
(
A
D
C
E
B
(第
8
题)
)连接.下列结论:①;②为等边三角形;
③; ④.其中结论正确的是( )
A.只有①② B.只有①②④ C.只有③④ D.①②③④
8. 如图,等腰△ABC中,底边,,的平分线交AC
于D,的平=线交BD于E,设,则( )
A. B. C. D.
9. 如图矩形纸片ABCD,AB=5cm,BC=10cm,CD上有一点E,ED=2cm,
AD上有一点P,PD=3cm,过P作PF⊥AD交BC于F,将纸片折叠,使P
点与E点重合,折痕与PF交于Q点,则PQ的长是________cm.
(
A
1
B
1
C
1
C
A
B
a
b
c
c
1
b
1
a
1
第
10
题图
)10. 如图,已知,相似比为k(k>1),且的三边长分别为a、b、c(a>b>c),的三边长分别为、、.
(1)若c=a1,求证:a=kc;(2)若c=a1,试给出符合条件
的一对和,使得a、b、c和、、都是
正整数,并加以说明;(3)若b=a1,c=b1,是否存在和使得k=2?请说明理由.
11. 如图,在平面直角坐标系中,点是坐标原点,四边形是梯形,,点的坐标为,点的坐标为,.(1)求点的坐标;
(2)点从点出发,沿线段以个单位/秒的速度向终点匀速运动,过点作,垂足为,设的面积为,点的运动时间为秒,求与之间的函数关系式(直接写出自变量的取值范围);
(
(第
11
题图)
(
第
11
题备用
图)
)(3)在(2)的条件下,过点作交线段于点,过点作,垂足为,线段分别交直线于点,点为线段的中点,连接.当为何值时,?
12. 在三角形纸片ABC中,已知∠ABC=90°,AB=6,BC=8。过点A作直线平行于BC,折叠三角形纸片ABC,使直角顶点B落在直线上的T处,折痕为MN.当点T在直线上移动时,折痕的端点M、N也随之移动.若限定端点M、N分别在AB、BC边上移动,则线段AT长度的最大值与最小值之和为_________ (计算结果不取近似值).
13.如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,
连接PM,PN,则下列结论:①PM=PN;②;③△PMN为等边三角形;
④当∠ABC=45°时,BN=PC.其中正确的个数是( )
A.1个 B 2个 C 3个 D4个
14.如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,
且∠DAE=45°,连接EF、BF,则下列结论:①△AED≌△AEF;
②△ABE∽△ACD;③BE+DC>DE;④BE2+DC2=DE2,其中正确的有( )个.
A 1 B 2 C 3 D 4
15. 如图,直角三角形中,,, ,
在线段上取一点,作交于点.现将沿
折叠,使点落在线段上,对应点记为;的中点的对应点记为.若∽,则=__________.
16.如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均
落在格点上.(Ⅰ)△ABC的面积等于 ;(Ⅱ)若四边形DEFG是△ABC中
所能包含的面积最大的正方形,请你在如图所示的网格中,用直尺和三角尺
画出该正方形,并简要说明画图方法(不要求证明).
17. 如图1,梯形ABCD中,AD∥BC,∠ABC=2∠BCD=2a,点E在AD上,点F在DC上,且∠BEF=∠A.(1)∠BEF=_____(用含a的代数式表示);(2)当AB=AD时,猜想线段ED、EF的数量关系,并证明你的猜想;(3)当AB≠AD时,将“点E在AD上”改为“点E在AD的延长线上,且AE>AB,AB=mDE,AD=nDE”,其他条件不变(如图2),求EB/EF的值(用含m、n的代数式表示)。
18. 已知△ABC中,AB=2,AC=4,BC=6.(1)如图1,点M为AB的中点,在线段AC上取点M,使△AMN与△ABC相似,求线段MN的长; (2)如图2,是由100个边长为1的小正方形组成的10×10的正方形网格,设顶点在这些小正方形顶点的三角形为格点三角形.①请你在所给的网格中画出格点△A1B1C1与全等(画出一个即可,不需证明);②试直接写出所给的网格中与相似且面积最大的格点三角形的个数,并画出其中一个(不需证明).
19. 已知∠ACD=90°,MN是过点A的直线,AC=DC,DB⊥MN于点B,如图(1).易证BD+AB=CB,过程如下:过点C作CE⊥CB于点C,与MN交于点E。∵∠ACB+∠BCD=90°,∠ACB+∠ACE=90°,∴∠BCD=∠ACE.∵四边形ACDB内角和为360°,∴∠BDC+∠CAB=180°.∵∠EAC+∠CAB=180°,∴∠EAC=∠BDC.又∵AC=DC,∴△ACE≌△DCB,∴AE=DB,CE=CB,∴△ECB为等腰直角三角形,∴BE=CB.又∵BE=AE+AB,∴BE=BD+AB,∴BD+AB=CB.
(1)当MN绕A旋转到如图(2)和图(3)两个位置时,BD、AB、CB满足什么样关系式,请写出你的猜想,并对图(2)给予证明.(2)MN在绕点A旋转过程中,当∠BCD=30°,BD=时,则CD= ,CB= .
20.已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与点B,C重合).以AD为边做正方形ADEF,连接CF。(1)如图1,当点D在线段BC上时.求证CF+CD=BC;
(2)如图2,当点D在线段BC的延长线上时,其他条件不变,请直接写出CF,BC,CD三条线段之间的关系;(3)如图3,当点D在线段BC的反向延长线上时,且点A,F分别在直线BC的两侧,其他条件不变;①请直接写出CF,BC,CD三条线段之间的关系;
②若正方形ADEF的边长为2,对角线AE,DF相交于点O,连接OC.求OC的长度.
21.如图,等腰梯形ABCD中,AD∥BC,∠B=45°,P是BC边上一点,△PAD的面积为,设AB=x,AD=y。(1)求y与x的函数关系式;(2)若∠APD=45°,当y=1时,求PB PC的值;
(3)若∠APD=90°,求y的最小值.
22.如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(6,0),
B(0.8),点C的坐标为(0,m),过点C作CE⊥AB于点E,点D为x轴上
的一动点,连接CD,DE,以CD,DE为边作四边形CDEF.
(1)当0<m<8时,求CE的长(用含m的代数式表示);
(2)当m=3时,是否存在点D,使四边形CDEF的顶点F恰好落在y轴上?
若存在,求出点D的坐标;若不存在,请说明理由;
(3)点D在整个运动过程中,若存在唯一的位置,使得四边形CDEF为矩形,
请求出所有满足条件的m的值.
同课章节目录
