2014年中考总复习第一轮教学案:第十一讲:圆
文档属性
| 名称 | 2014年中考总复习第一轮教学案:第十一讲:圆 |

|
|
| 格式 | zip | ||
| 文件大小 | 211.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-02-04 00:00:00 | ||
图片预览

文档简介
2014年中考总复习第一轮: 第十一讲:圆
一.知识点:1.圆的概念:⑴圆的定义;⑵点与圆的位置关系;⑶基本概念:弦、直径、弦心距、弧、半圆、优弧、劣弧、等弧、弓形、等圆;⑷圆的确定性:圆心、半径;⑸圆的有关性质:①对称性②垂径定理及其推论③圆的两条平行弦所夹的弧相等④圆心角、弧、弦、弦心距之间的关系;2.圆心角与圆周角:⑴定义 ⑵重要定理及其性质⑶圆的内接四边形3.直线与圆:⑴位置关系及其数量特征;⑵切线的性质与判定⑶三角形的内切圆4.圆与圆的位置关系:⑴位置关系 ⑵数量特征 ⑶重要性质 ⑷公切线 5.圆的有关计算:弧长、扇形面积、圆柱的表面积及体积、圆锥的表面积及体积、展开图。6.有关其他的圆知识拓展。
二.本节在中考中的位置、难度、分值:填空、选择居多,不排除出大题的可能,中等题。分值3-6分.
(
A
D
C
B
O
E
F
(第1题)
)三.注意的问题:1.重视垂径定理;2.圆的有关计算;3.切线的性质与判定也有可能出题;4.出综合题的可能性比较大。
四.针对性训练
1. 以正方形的边为直径作半圆,过点作直线切半圆于点,
交边于点,则三角形和直角梯形周长之比为( )
A. B. C. D.
(
图
3
B
A
C
D
E
O
)2. 如图2,边长为1的菱形ABCD绕点A旋转,当B、C两点恰好落在扇形AEF的
弧EF上时,弧BC的长度等于( )
A. B. C. D.
3. 如图3所示,边长为1的小正方形构成的网格中,
半径为1的⊙O的圆心O在格点上,则∠AED的正切
值等于 .
4. 如图9,等边边长为4,是边上动点,
于H,过作∥,交线段于点,
在线段上取点,使。设。
⑴⑵⑶请直接写出图中与线段相等的两条线段(不再另外添加辅助线);
是线段上的动点,当四边形是平行四边形时,求 的面积(用含的代数式表示);
(3) 当(2)中 的面积最大值时,以E为圆心,为半径作圆,
根据⊙E与此时四条边交点的总个数,求相应的的取值范围。
5.如图,在△ABC中,∠BAC=90°,BM平分∠ABC交AC于M,以A为圆心,AM为
半径作OA交BM于N,AN的延长线交BC于D,直线AB交OA于P、K两点.作
MT⊥BC于T. (1)求证AK=MT; (2)求证:AD⊥BC;
(3)当AK=BD时,求证:.
6. 如图,在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,
(
第
7
题图
A
D
E
F
C
B
)函数y=x的图象被⊙P的弦AB的长为,则a的值是( )
A. B. C. D.
7. 如图,已知正方形ABCD的对角线长为2,将正方
形ABCD沿直线EF折叠,则图中阴影部分的周长为( )
A.8 B. 4 C.8 D.6
8. 如图,⊙A与⊙B外切于点D,PC,PD,PE分别是圆的切线,C,D,E是切点,
若∠CED=°,∠ECD=°,⊙B的半径为R,则的长度是( )
A. B.C. D.
9. 如图,AB,CD是⊙O的两条互相垂直的直径,
点O1,O2,O3,O4分别是OA、OB、OC、OD的中点,
若⊙O的半径为2,则阴影部分的面积为( )
A.8 B.4 C.4π+4 D.4π﹣4
(
C
A
B
C
G
H
E
F
第
11
题图
)10. 如图,AE是半圆O的直径,弦AB=BC=4,弦CD=DE=4,
连结OB,OD,则图中两个阴影部分的面积和为 .
11. 图,AB是⊙O的一条弦,点C是⊙O上一动点,
且∠ACB=30°,点E、F分别是AC、BC的中点,
直线EF与⊙O交于G、H两点,若⊙O的半径为7,
则GE+FH的最大值为 .
12. 在△ABC中,∠C为锐角,分别以AB,AC为直径作半圆,过点B,A,
C作,如图所示.若AB=4,AC=2,S1﹣S2=,则S3﹣S4的值是( )
A B C D
13. 对于平面直角坐标系中的点P和⊙C,给出如下定义:若⊙C上存在两个点A,B,使得∠APB=60°,则称P为⊙C 的关联点。已知点D ,E(0,-2),F(,0)
(1)当⊙O的半径为1时,①在点D,E,F中,⊙O的关联点是__________;
②过点F作直线交轴正半轴于点G,使∠GFO=30°,若直线上的点P(,)是⊙O的关联点,求的取值范围;
(2)若线段EF上的所有点都是某个圆的关联点,求这个圆的半径的取值范围。
14. 如图,⊙O的半径为1,直线CD经过圆心O,交⊙O于C、D两点,直径AB⊥CD,点M是直线CD上异于点C、O、D的一个动点,AM所在的直线交于⊙O于点N,点P是直线CD上另一点,且PM=PN.
(1)当点M在⊙O内部,如图一,试判断PN与⊙O的关系,并写出证明过程;
(2)当点M在⊙O外部,如图二,其它条件不变时,(1)的结论是否还成立?请说明理由;
(3)当点M在⊙O外部,如图三,∠AMO=15°,求图中阴影部分的面积.
15. 如图,AB为⊙O的直径,EF切⊙O于点D,过点B作BH⊥EF于点H,
交⊙O于点C,连接BD.
(1)求证:BD平分∠ABH;
(2)如果AB=12,BC=8,求圆心O到BC的距离.
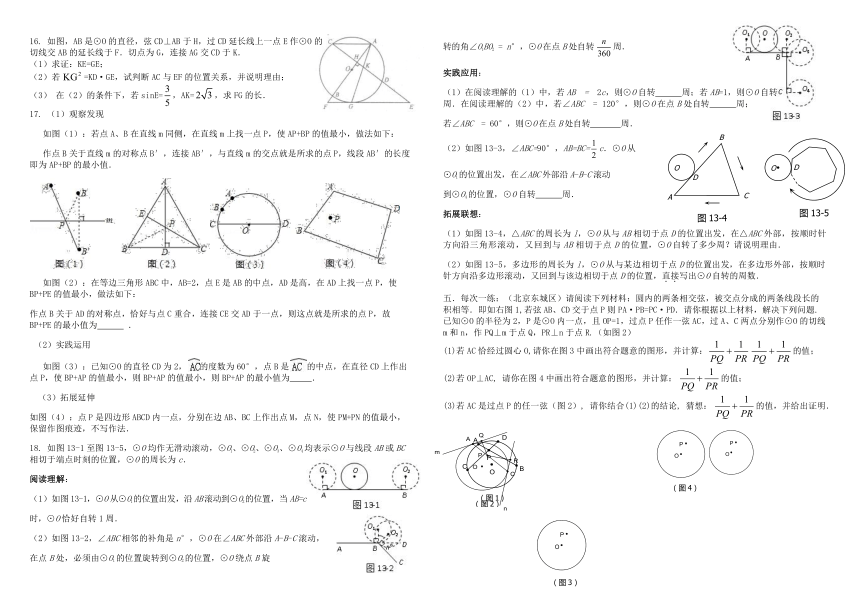
16. 如图,AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的
切线交AB的延长线于F.切点为G,连接AG交CD于K.
(1)求证:KE=GE;
(2)若=KD·GE,试判断AC与EF的位置关系,并说明理由;
(3) 在(2)的条件下,若sinE=,AK=,求FG的长.
17. (1)观察发现
如图(1):若点A、B在直线m同侧,在直线m上找一点P,使AP+BP的值最小,做法如下:
作点B关于直线m的对称点B′,连接AB′,与直线m的交点就是所求的点P,线段AB′的长度即为AP+BP的最小值.
如图(2):在等边三角形ABC中,AB=2,点E是AB的中点,AD是高,在AD上找一点P,使BP+PE的值最小,做法如下:
作点B关于AD的对称点,恰好与点C重合,连接CE交AD于一点,则这点就是所求的点P,故BP+PE的最小值为 .
(2)实践运用
如图(3):已知⊙O的直径CD为2,的度数为60°,点B是的中点,在直径CD上作出点P,使BP+AP的值最小,则BP+AP的值最小,则BP+AP的最小值为 .
(3)拓展延伸
如图(4):点P是四边形ABCD内一点,分别在边AB、BC上作出点M,点N,使PM+PN的值最小,保留作图痕迹,不写作法.
18. 如图13-1至图13-5,⊙O均作无滑动滚动,⊙O1、⊙O2、⊙O3、⊙O4均表示⊙O与线段AB或BC相切于端点时刻的位置,⊙O的周长为c.
阅读理解:
(1)如图13-1,⊙O从⊙O1的位置出发,沿AB滚动到⊙O2的位置,当AB=c
时,⊙O恰好自转1周.
(2)如图13-2,∠ABC相邻的补角是n°,⊙O在∠ABC外部沿A-B-C滚动,
在点B处,必须由⊙O1的位置旋转到⊙O2的位置,⊙O绕点B旋
转的角∠O1BO2 = n°,⊙O在点B处自转周.
实践应用:
(1)在阅读理解的(1)中,若AB = 2c,则⊙O自转 周;若AB=1,则⊙O自转 周.在阅读理解的(2)中,若∠ABC = 120°,则⊙O在点B处自转 周;
若∠ABC = 60°,则⊙O (
O
A
B
C
图
13-4
D
)在点B处自转 周.
(
D
图
13-5
O
)(2)如图13-3,∠ABC=90°,AB=BC=c.⊙O从
⊙O1的位置出发,在∠ABC外部沿A-B-C滚动
到⊙O4的位置,⊙O自转 周.
拓展联想:
(1)如图13-4,△ABC的周长为l,⊙O从与AB相切于点D的位置出发,在△ABC外部,按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,⊙O自转了多少周?请说明理由.
(2)如图13-5,多边形的周长为l,⊙O从与某边相切于点D的位置出发,在多边形外部,按顺时针方向沿多边形滚动,又回到与该边相切于点D的位置,直接写出⊙O自转的周数.
五.每次一练:(北京东城区)请阅读下列材料:圆内的两条相交弦,被交点分成的两条线段长的积相等.即如右图1,若弦AB、CD交于点P则PA·PB=PC·PD.请你根据以上材料,解决下列问题.
已知⊙O的半径为2,P是⊙O内一点,且OP=1,过点P任作一弦AC,过A、C两点分别作⊙O的切线m和n,作PQ⊥m于点Q,PR⊥n于点R.(如图2)
(1)若AC恰经过圆心O,请你在图3中画出符合题意的图形,并计算:的值;
(2)若OP⊥AC, 请你在图4中画出符合题意的图形,并计算:的值;
(3)若AC是过点P的任一弦(图2), 请你结合(1)(2)的结论, 猜想:的值,并给出证明.
(
(图
4
)
) (
(图
2
)
) (
(图
1
)
)
(
(图
3
)
)
一.知识点:1.圆的概念:⑴圆的定义;⑵点与圆的位置关系;⑶基本概念:弦、直径、弦心距、弧、半圆、优弧、劣弧、等弧、弓形、等圆;⑷圆的确定性:圆心、半径;⑸圆的有关性质:①对称性②垂径定理及其推论③圆的两条平行弦所夹的弧相等④圆心角、弧、弦、弦心距之间的关系;2.圆心角与圆周角:⑴定义 ⑵重要定理及其性质⑶圆的内接四边形3.直线与圆:⑴位置关系及其数量特征;⑵切线的性质与判定⑶三角形的内切圆4.圆与圆的位置关系:⑴位置关系 ⑵数量特征 ⑶重要性质 ⑷公切线 5.圆的有关计算:弧长、扇形面积、圆柱的表面积及体积、圆锥的表面积及体积、展开图。6.有关其他的圆知识拓展。
二.本节在中考中的位置、难度、分值:填空、选择居多,不排除出大题的可能,中等题。分值3-6分.
(
A
D
C
B
O
E
F
(第1题)
)三.注意的问题:1.重视垂径定理;2.圆的有关计算;3.切线的性质与判定也有可能出题;4.出综合题的可能性比较大。
四.针对性训练
1. 以正方形的边为直径作半圆,过点作直线切半圆于点,
交边于点,则三角形和直角梯形周长之比为( )
A. B. C. D.
(
图
3
B
A
C
D
E
O
)2. 如图2,边长为1的菱形ABCD绕点A旋转,当B、C两点恰好落在扇形AEF的
弧EF上时,弧BC的长度等于( )
A. B. C. D.
3. 如图3所示,边长为1的小正方形构成的网格中,
半径为1的⊙O的圆心O在格点上,则∠AED的正切
值等于 .
4. 如图9,等边边长为4,是边上动点,
于H,过作∥,交线段于点,
在线段上取点,使。设。
⑴⑵⑶请直接写出图中与线段相等的两条线段(不再另外添加辅助线);
是线段上的动点,当四边形是平行四边形时,求 的面积(用含的代数式表示);
(3) 当(2)中 的面积最大值时,以E为圆心,为半径作圆,
根据⊙E与此时四条边交点的总个数,求相应的的取值范围。
5.如图,在△ABC中,∠BAC=90°,BM平分∠ABC交AC于M,以A为圆心,AM为
半径作OA交BM于N,AN的延长线交BC于D,直线AB交OA于P、K两点.作
MT⊥BC于T. (1)求证AK=MT; (2)求证:AD⊥BC;
(3)当AK=BD时,求证:.
6. 如图,在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,
(
第
7
题图
A
D
E
F
C
B
)函数y=x的图象被⊙P的弦AB的长为,则a的值是( )
A. B. C. D.
7. 如图,已知正方形ABCD的对角线长为2,将正方
形ABCD沿直线EF折叠,则图中阴影部分的周长为( )
A.8 B. 4 C.8 D.6
8. 如图,⊙A与⊙B外切于点D,PC,PD,PE分别是圆的切线,C,D,E是切点,
若∠CED=°,∠ECD=°,⊙B的半径为R,则的长度是( )
A. B.C. D.
9. 如图,AB,CD是⊙O的两条互相垂直的直径,
点O1,O2,O3,O4分别是OA、OB、OC、OD的中点,
若⊙O的半径为2,则阴影部分的面积为( )
A.8 B.4 C.4π+4 D.4π﹣4
(
C
A
B
C
G
H
E
F
第
11
题图
)10. 如图,AE是半圆O的直径,弦AB=BC=4,弦CD=DE=4,
连结OB,OD,则图中两个阴影部分的面积和为 .
11. 图,AB是⊙O的一条弦,点C是⊙O上一动点,
且∠ACB=30°,点E、F分别是AC、BC的中点,
直线EF与⊙O交于G、H两点,若⊙O的半径为7,
则GE+FH的最大值为 .
12. 在△ABC中,∠C为锐角,分别以AB,AC为直径作半圆,过点B,A,
C作,如图所示.若AB=4,AC=2,S1﹣S2=,则S3﹣S4的值是( )
A B C D
13. 对于平面直角坐标系中的点P和⊙C,给出如下定义:若⊙C上存在两个点A,B,使得∠APB=60°,则称P为⊙C 的关联点。已知点D ,E(0,-2),F(,0)
(1)当⊙O的半径为1时,①在点D,E,F中,⊙O的关联点是__________;
②过点F作直线交轴正半轴于点G,使∠GFO=30°,若直线上的点P(,)是⊙O的关联点,求的取值范围;
(2)若线段EF上的所有点都是某个圆的关联点,求这个圆的半径的取值范围。
14. 如图,⊙O的半径为1,直线CD经过圆心O,交⊙O于C、D两点,直径AB⊥CD,点M是直线CD上异于点C、O、D的一个动点,AM所在的直线交于⊙O于点N,点P是直线CD上另一点,且PM=PN.
(1)当点M在⊙O内部,如图一,试判断PN与⊙O的关系,并写出证明过程;
(2)当点M在⊙O外部,如图二,其它条件不变时,(1)的结论是否还成立?请说明理由;
(3)当点M在⊙O外部,如图三,∠AMO=15°,求图中阴影部分的面积.
15. 如图,AB为⊙O的直径,EF切⊙O于点D,过点B作BH⊥EF于点H,
交⊙O于点C,连接BD.
(1)求证:BD平分∠ABH;
(2)如果AB=12,BC=8,求圆心O到BC的距离.
16. 如图,AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的
切线交AB的延长线于F.切点为G,连接AG交CD于K.
(1)求证:KE=GE;
(2)若=KD·GE,试判断AC与EF的位置关系,并说明理由;
(3) 在(2)的条件下,若sinE=,AK=,求FG的长.
17. (1)观察发现
如图(1):若点A、B在直线m同侧,在直线m上找一点P,使AP+BP的值最小,做法如下:
作点B关于直线m的对称点B′,连接AB′,与直线m的交点就是所求的点P,线段AB′的长度即为AP+BP的最小值.
如图(2):在等边三角形ABC中,AB=2,点E是AB的中点,AD是高,在AD上找一点P,使BP+PE的值最小,做法如下:
作点B关于AD的对称点,恰好与点C重合,连接CE交AD于一点,则这点就是所求的点P,故BP+PE的最小值为 .
(2)实践运用
如图(3):已知⊙O的直径CD为2,的度数为60°,点B是的中点,在直径CD上作出点P,使BP+AP的值最小,则BP+AP的值最小,则BP+AP的最小值为 .
(3)拓展延伸
如图(4):点P是四边形ABCD内一点,分别在边AB、BC上作出点M,点N,使PM+PN的值最小,保留作图痕迹,不写作法.
18. 如图13-1至图13-5,⊙O均作无滑动滚动,⊙O1、⊙O2、⊙O3、⊙O4均表示⊙O与线段AB或BC相切于端点时刻的位置,⊙O的周长为c.
阅读理解:
(1)如图13-1,⊙O从⊙O1的位置出发,沿AB滚动到⊙O2的位置,当AB=c
时,⊙O恰好自转1周.
(2)如图13-2,∠ABC相邻的补角是n°,⊙O在∠ABC外部沿A-B-C滚动,
在点B处,必须由⊙O1的位置旋转到⊙O2的位置,⊙O绕点B旋
转的角∠O1BO2 = n°,⊙O在点B处自转周.
实践应用:
(1)在阅读理解的(1)中,若AB = 2c,则⊙O自转 周;若AB=1,则⊙O自转 周.在阅读理解的(2)中,若∠ABC = 120°,则⊙O在点B处自转 周;
若∠ABC = 60°,则⊙O (
O
A
B
C
图
13-4
D
)在点B处自转 周.
(
D
图
13-5
O
)(2)如图13-3,∠ABC=90°,AB=BC=c.⊙O从
⊙O1的位置出发,在∠ABC外部沿A-B-C滚动
到⊙O4的位置,⊙O自转 周.
拓展联想:
(1)如图13-4,△ABC的周长为l,⊙O从与AB相切于点D的位置出发,在△ABC外部,按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,⊙O自转了多少周?请说明理由.
(2)如图13-5,多边形的周长为l,⊙O从与某边相切于点D的位置出发,在多边形外部,按顺时针方向沿多边形滚动,又回到与该边相切于点D的位置,直接写出⊙O自转的周数.
五.每次一练:(北京东城区)请阅读下列材料:圆内的两条相交弦,被交点分成的两条线段长的积相等.即如右图1,若弦AB、CD交于点P则PA·PB=PC·PD.请你根据以上材料,解决下列问题.
已知⊙O的半径为2,P是⊙O内一点,且OP=1,过点P任作一弦AC,过A、C两点分别作⊙O的切线m和n,作PQ⊥m于点Q,PR⊥n于点R.(如图2)
(1)若AC恰经过圆心O,请你在图3中画出符合题意的图形,并计算:的值;
(2)若OP⊥AC, 请你在图4中画出符合题意的图形,并计算:的值;
(3)若AC是过点P的任一弦(图2), 请你结合(1)(2)的结论, 猜想:的值,并给出证明.
(
(图
4
)
) (
(图
2
)
) (
(图
1
)
)
(
(图
3
)
)
同课章节目录
