有理不等式的解法[上学期]
图片预览






文档简介
(共16张PPT)
有理不等式的解法
新疆奎屯市一中
王新敞
基本概念
1、同解不等式:
2、同解变形:
如果两个不等式的解集相等,那么这两个不等式就叫做同解不等式。
一个不等式变形为另一个不等式时,如果这两个不等式是同解不等式,那么这种变形叫做不等式的同解变形。
一元一次不等式的解法:
任何一个一元一次不等式,经过不等式的同解变形后。都可以化成
的形式。
其解集为:
例1 解不等式
解:两边都乘以6,得
移项,整理后,得
两边除以-7,得解集
一次不等式的解法_---------
例2 解不等式组
解:因为各不等式的解集分别为
所以不等式的解集是
一次不等式组的解法_---------
一元二次不等式的解法
例3 解不等式
解:原不等式可变形为
因为
解方程
得
所以原不等式的解集是
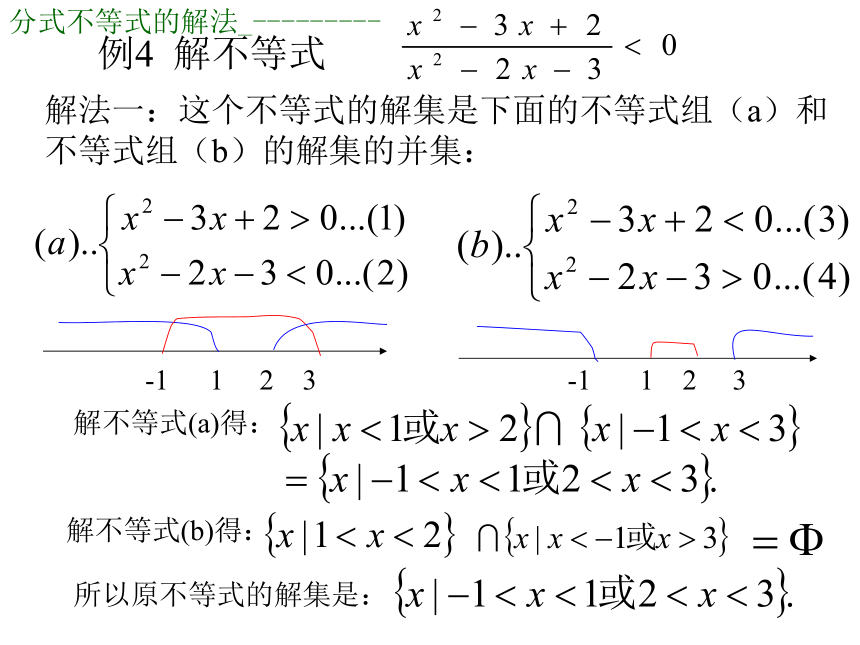
例4 解不等式
解法一:这个不等式的解集是下面的不等式组(a)和不等式组(b)的解集的并集:
解不等式(a)得:
解不等式(b)得:
所以原不等式的解集是:
-1
1
2
3
-1
1
2
3
分式不等式的解法_---------
解法二:
原不等式可化为:
把分子分母各因式的根按从小到大的顺序排列,可得下表:
x+1
x-1
x-2
x-3
因式
根
各因式的值的符号
-1
1
2
3
-
+
+
+
+
-
-
+
+
+
-
-
-
+
+
-
-
-
-
+
+
-
+
-
+
由上表可知,原不等式的解集为:
分式不等式的解法_---------
解:原不等式可化为:
把各因式的根按从小到大的顺序排列,可得下表:
x
x+1
x-2
x-3
因式
根
各因式的值的符号
0
-1
2
3
-
+
+
+
+
-
-
+
+
+
-
-
-
+
+
-
-
-
-
+
+
-
+
-
+
由上表可知,原不等式的解集为:
例5 解不等式
高次不等式的解法-------
有理不等式的课堂练习1
答案:
(1)
(2)
有理不等式的课堂练习2
答案:
(1)
(2)
有理不等式的课堂练习3
答案:
(1)
(2)
(3)
有理不等式的课堂练习4
答案:
(1)
(2)
有理不等式的课堂练习5
答案:
1
2
3
4
+
+
+
-
-
有理不等式的课堂练习6
答案:
-1
0
2
3
+
+
+
-
-
作业:
祝同学们天天进步!
有理不等式的解法
新疆奎屯市一中
王新敞
基本概念
1、同解不等式:
2、同解变形:
如果两个不等式的解集相等,那么这两个不等式就叫做同解不等式。
一个不等式变形为另一个不等式时,如果这两个不等式是同解不等式,那么这种变形叫做不等式的同解变形。
一元一次不等式的解法:
任何一个一元一次不等式,经过不等式的同解变形后。都可以化成
的形式。
其解集为:
例1 解不等式
解:两边都乘以6,得
移项,整理后,得
两边除以-7,得解集
一次不等式的解法_---------
例2 解不等式组
解:因为各不等式的解集分别为
所以不等式的解集是
一次不等式组的解法_---------
一元二次不等式的解法
例3 解不等式
解:原不等式可变形为
因为
解方程
得
所以原不等式的解集是
例4 解不等式
解法一:这个不等式的解集是下面的不等式组(a)和不等式组(b)的解集的并集:
解不等式(a)得:
解不等式(b)得:
所以原不等式的解集是:
-1
1
2
3
-1
1
2
3
分式不等式的解法_---------
解法二:
原不等式可化为:
把分子分母各因式的根按从小到大的顺序排列,可得下表:
x+1
x-1
x-2
x-3
因式
根
各因式的值的符号
-1
1
2
3
-
+
+
+
+
-
-
+
+
+
-
-
-
+
+
-
-
-
-
+
+
-
+
-
+
由上表可知,原不等式的解集为:
分式不等式的解法_---------
解:原不等式可化为:
把各因式的根按从小到大的顺序排列,可得下表:
x
x+1
x-2
x-3
因式
根
各因式的值的符号
0
-1
2
3
-
+
+
+
+
-
-
+
+
+
-
-
-
+
+
-
-
-
-
+
+
-
+
-
+
由上表可知,原不等式的解集为:
例5 解不等式
高次不等式的解法-------
有理不等式的课堂练习1
答案:
(1)
(2)
有理不等式的课堂练习2
答案:
(1)
(2)
有理不等式的课堂练习3
答案:
(1)
(2)
(3)
有理不等式的课堂练习4
答案:
(1)
(2)
有理不等式的课堂练习5
答案:
1
2
3
4
+
+
+
-
-
有理不等式的课堂练习6
答案:
-1
0
2
3
+
+
+
-
-
作业:
祝同学们天天进步!
