山东 数系的扩充与复数的概念[下学期]
文档属性
| 名称 | 山东 数系的扩充与复数的概念[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 257.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-04-10 00:00:00 | ||
图片预览



文档简介
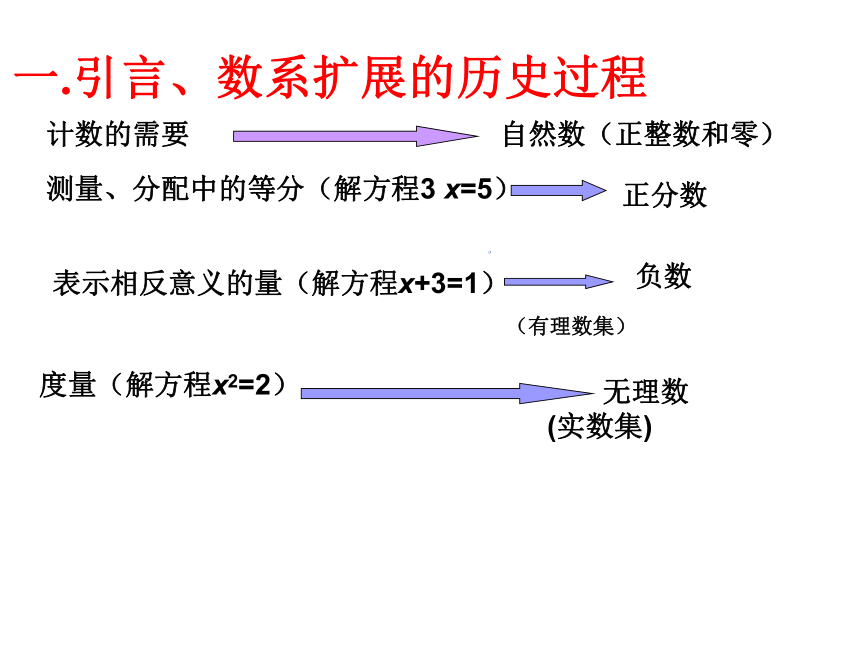
课件19张PPT。 引言:在人和社会的发展过程中,常常需要立足今天,回顾昨天,展望明天。符合客观发展规律的要发扬和完善,不符合的要否定和抛弃。那么,在实数集向复数集发展的过程中,我们应该如何发扬和完善,否定和抛弃呢?数系的扩充与复数的概念一.引言、数系扩展的历史过程计数的需要自然数(正整数和零)表示相反意义的量(解方程x+3=1)负数测量、分配中的等分(解方程3 x=5)正分数度量(解方程x2=2)
无理数
(实数集)
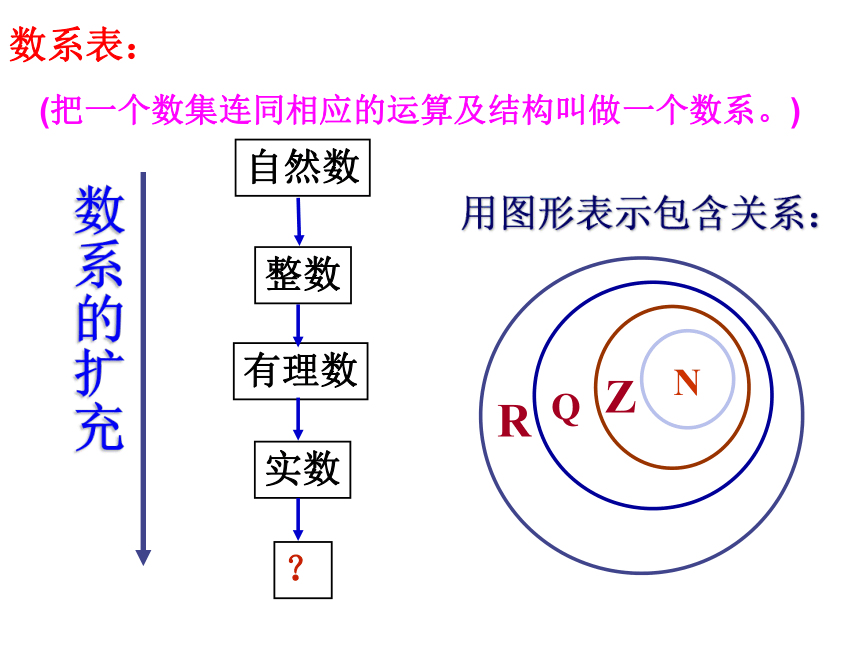
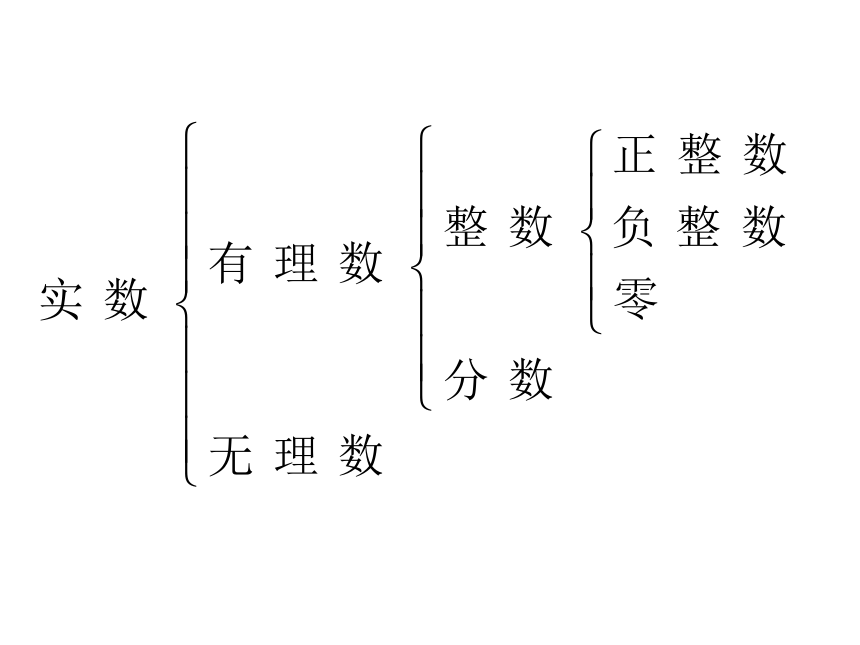
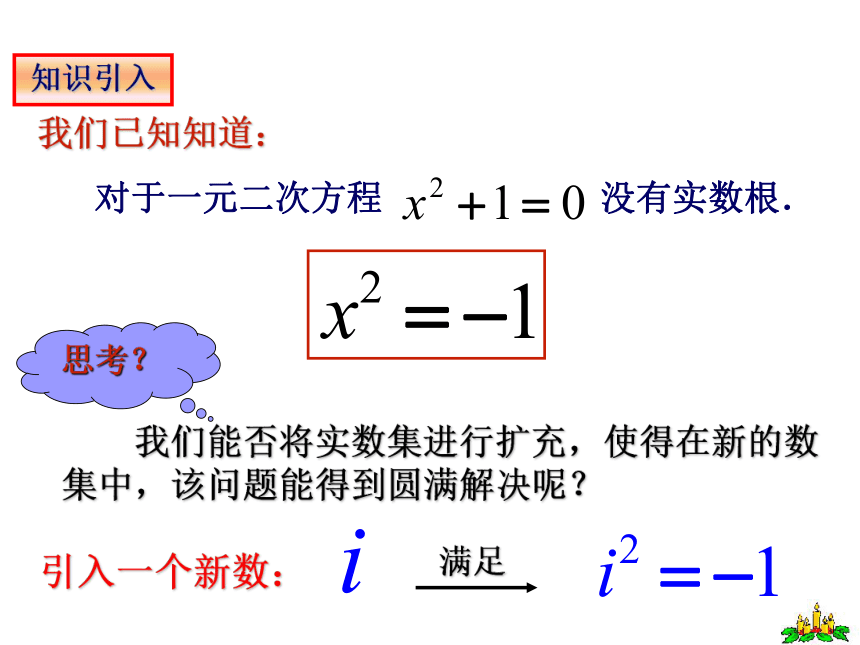
(有理数集)数系的扩充用图形表示包含关系:(把一个数集连同相应的运算及结构叫做一个数系。)数系表:知识引入引入一个新数:练习:解方程 .以上方程的根可以统一表示为 a+bi (a,b为实数)的形式。复数的代数形式:通常用字母 z 表示,即其中 称为虚数单位。复数a+bi复数集,虚数集,实数集,纯虚数集之间的关系? 思 考?复数集虚数集实数集纯虚数集复 数 实数虚数有理数无理数整数分数自然数负整数纯虚数非纯虚数例1.说明下列数是否是虚数,并说明各数的实部与虚部例2.实数 m 取什么数值时,复数z=m +1+(m-1)i是:
(1)实数? (2)虚数?(3)纯虚数?解:复数z=m+1+(m-1)i 中,因为m∈R,所以m+1,m-1都是实数,它们分别是z的实部和虚部,∴ (1)m=1时,z是实数;
(2)m≠1时,z是虚数;练一练:1.说明下列数中,那些是实数,哪些是虚数,哪些是纯虚数,并指出复数的实部与虚部。5 +8,02、判断下列命题是否正确:
(1)若a、b为实数,则Z=a+bi为虚数
(2)若b为实数,则Z=bi必为纯虚数
(3)若a为实数,则Z= a一定不是虚数思考:如何定义两个复数的相等?注意:一般对两个不全是的复数只能说相等或不相等;不能比较大小。 如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.a+bi =0例2 已知 ,其中 求解题思考:复数相等的问题转化求方程组的解的问题一种重要的数学思想:转化思想-12小结:2.虚数单位i的引入;1.数集的扩充
无理数
(实数集)
(有理数集)数系的扩充用图形表示包含关系:(把一个数集连同相应的运算及结构叫做一个数系。)数系表:知识引入引入一个新数:练习:解方程 .以上方程的根可以统一表示为 a+bi (a,b为实数)的形式。复数的代数形式:通常用字母 z 表示,即其中 称为虚数单位。复数a+bi复数集,虚数集,实数集,纯虚数集之间的关系? 思 考?复数集虚数集实数集纯虚数集复 数 实数虚数有理数无理数整数分数自然数负整数纯虚数非纯虚数例1.说明下列数是否是虚数,并说明各数的实部与虚部例2.实数 m 取什么数值时,复数z=m +1+(m-1)i是:
(1)实数? (2)虚数?(3)纯虚数?解:复数z=m+1+(m-1)i 中,因为m∈R,所以m+1,m-1都是实数,它们分别是z的实部和虚部,∴ (1)m=1时,z是实数;
(2)m≠1时,z是虚数;练一练:1.说明下列数中,那些是实数,哪些是虚数,哪些是纯虚数,并指出复数的实部与虚部。5 +8,02、判断下列命题是否正确:
(1)若a、b为实数,则Z=a+bi为虚数
(2)若b为实数,则Z=bi必为纯虚数
(3)若a为实数,则Z= a一定不是虚数思考:如何定义两个复数的相等?注意:一般对两个不全是的复数只能说相等或不相等;不能比较大小。 如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.a+bi =0例2 已知 ,其中 求解题思考:复数相等的问题转化求方程组的解的问题一种重要的数学思想:转化思想-12小结:2.虚数单位i的引入;1.数集的扩充
