复数的概念[上学期]
图片预览



文档简介
课件8张PPT。复数的概念1、定义: i叫虚数单位,规定:
(1)i2=-1
(2)实数可以与它进行四则运算,进行四则运算时,原有的加、乘运算律仍然成立。表示:z=a+bi(a,b R)叫复数的代数形式。
a、b分别叫做复数的实部、虚部。
2、定义:
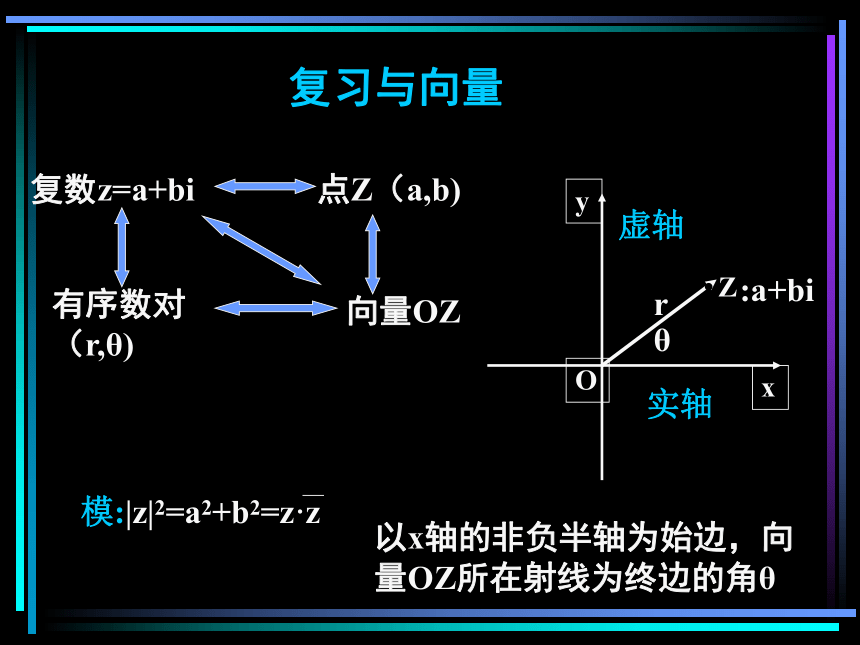
形如a+bi(a,b R)的数叫做复数,全体复数所成的集合叫复数集,用字母C表示。a=0,b≠0,则z=bi叫纯虚数。b≠0,则z=a+bi叫虚数。虚部不为0是两个共轭复数叫共轭虚数。复习与向量复数z=a+bi Zr:a+bi实轴虚轴θ例1、实数m取什么数值时,复数z=m+1+(m-1)i是
(1)实数?(2)虚数?(3)纯虚数?例2、m取何实数时,复数
是实数?是虚数?是纯虚数?m=1m≠1m=-1m=5m≠5 切m≠-3m=3 切m=-2例3、复数
试分别求满足下列条件的 m :
(1)z为纯虚数;(2)z=0m=-1m=44、复数相等:
如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等。(1)复数相等的意义:
求复数值,在复数集中解方程的重要依据。(2)两个复数只能说相等,不相等;不能比较大小。例5 若关于x的方程
有实数解,求实数a的值。x=2.5; y=4a=-3时x=-1a=7/3时x=3
(1)i2=-1
(2)实数可以与它进行四则运算,进行四则运算时,原有的加、乘运算律仍然成立。表示:z=a+bi(a,b R)叫复数的代数形式。
a、b分别叫做复数的实部、虚部。
2、定义:
形如a+bi(a,b R)的数叫做复数,全体复数所成的集合叫复数集,用字母C表示。a=0,b≠0,则z=bi叫纯虚数。b≠0,则z=a+bi叫虚数。虚部不为0是两个共轭复数叫共轭虚数。复习与向量复数z=a+bi Zr:a+bi实轴虚轴θ例1、实数m取什么数值时,复数z=m+1+(m-1)i是
(1)实数?(2)虚数?(3)纯虚数?例2、m取何实数时,复数
是实数?是虚数?是纯虚数?m=1m≠1m=-1m=5m≠5 切m≠-3m=3 切m=-2例3、复数
试分别求满足下列条件的 m :
(1)z为纯虚数;(2)z=0m=-1m=44、复数相等:
如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等。(1)复数相等的意义:
求复数值,在复数集中解方程的重要依据。(2)两个复数只能说相等,不相等;不能比较大小。例5 若关于x的方程
有实数解,求实数a的值。x=2.5; y=4a=-3时x=-1a=7/3时x=3
