山东 复数的复习课[下学期]

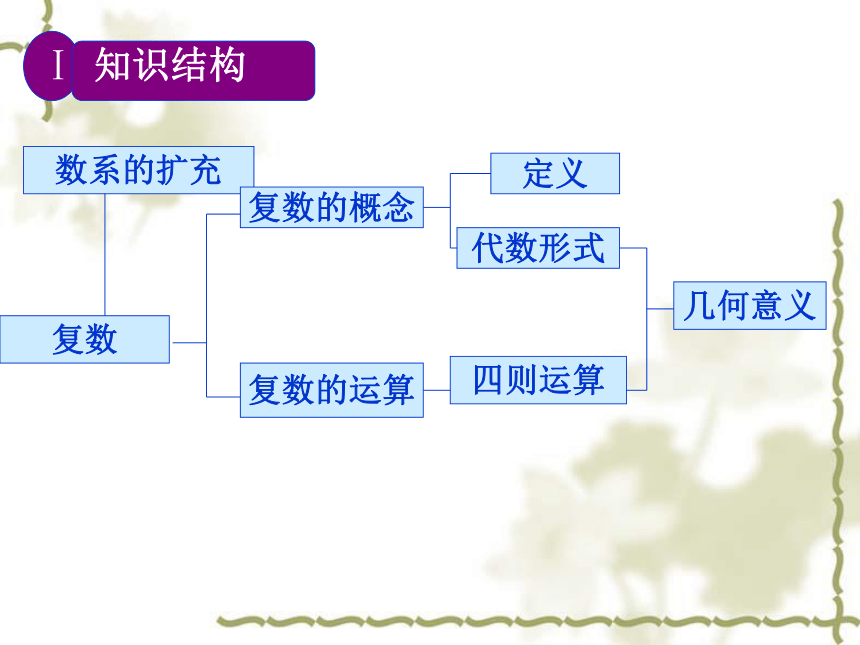
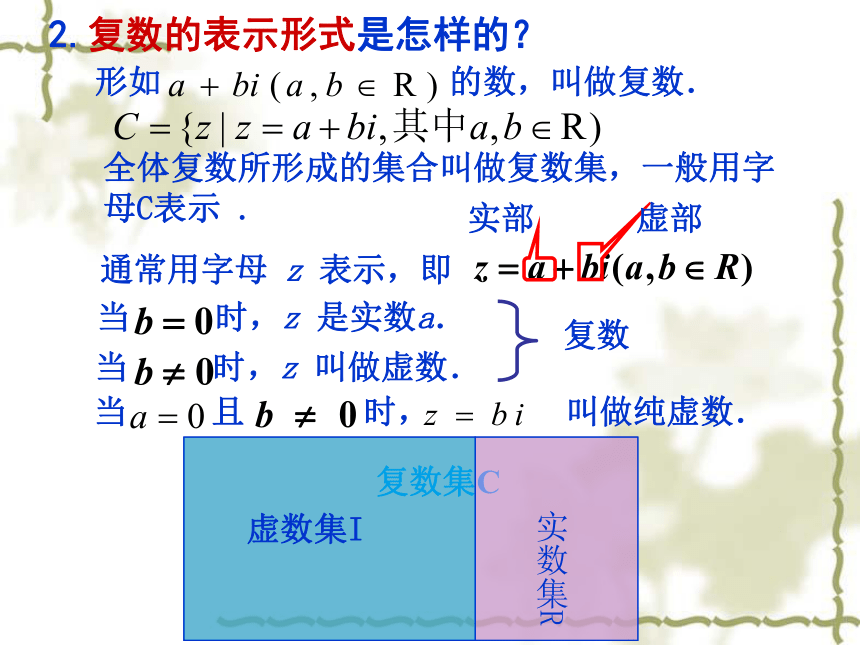
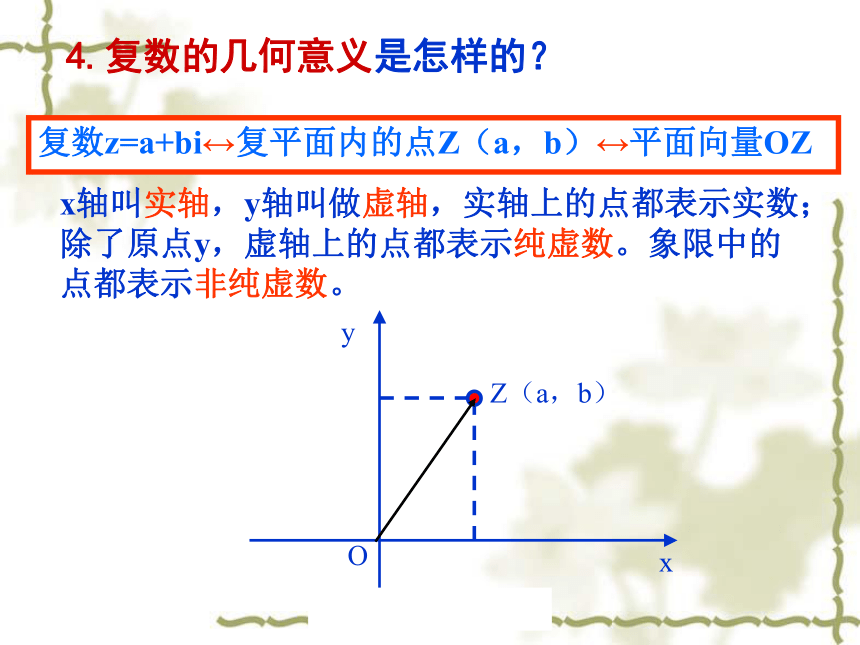
课件27张PPT。复数复习课知识结构Ⅰ知识结构几何意义根据对虚数单位i的运算规定易知： 1.虚数单位是怎样定义的？虚数单位，规定：（2）实数可以与它进行四则运算，进行四则运算时，原有的加、乘运算律仍然成立．Ⅱ基础知识形如 的数，叫做复数． 全体复数所形成的集合叫做复数集，一般用字母C表示 . 2.复数的表示形式是怎样的？当 时，z 是实数a．当 时，z 叫做虚数．当 且 时， 叫做纯虚数．如果两个复数的实部和虚部分别相等，那么我们就说这两个复数相等．即如果 ，那么3.两复数相等的充要条件是什么？x轴叫实轴，y轴叫做虚轴，实轴上的点都表示实数；除了原点y，虚轴上的点都表示纯虚数。象限中的点都表示非纯虚数。复数z=a+bi?复平面内的点Z（a，b）?平面向量OZ4.复数的几何意义是怎样的？5、复数的加法法则6、复数的减法法则（a+bi）-（c+di）=（a-c）+（b-d）i。注：两个复数相加（减）就是把实部与实部、虚部与虚部分别相加（减），即
（a+bi）±（c+di）=（a ± c） + （b±d）i（a+bi）+（c+di）=（a+c）+（b+d）i7、复数的乘法z1·z2=(a+bi)(c+di)=注：1、复数的乘法与多项式的乘法类似，但必须在所得的结果中把i2 换成-1，并把实部与虚部分开。ac+bci+adi+bdi2=(ac-bd)+(ad+bc)i8、复数的除法（a+bi）÷ （c+di) 或9、补充概念。(5)复数的模可以比较大小，一般地，两个复数不能比较大小，除非两个复数都是实数才可以比较大小。（4.）复数的倒数：且有（6）复数的模（7）复数与点的轨迹三、常用结论1. 特殊复数：2. 关于复数的共轭：3. 关于复数的模：例1判断以下命题的真假：⑴ 实数不是复数；（5）复平面内x轴是实轴，y轴是虚轴；（6）虚轴上的点对应的复数都是纯虚数；（8）实数集R与纯虚数集{bi}（b∈R）是一一对应的；（9）复数集C与复平面内的向量组成的集合一一对应；真假假假假假假假假真例3 已知z∈C，复数几何意义的运用练习(1):已知：复数 满足求： 的最值。表示 上的点到点 的距离。如图，可得：解析：综合计算： 例3 计算： 例5 已知z∈C，