充要条件[上学期]
图片预览




文档简介
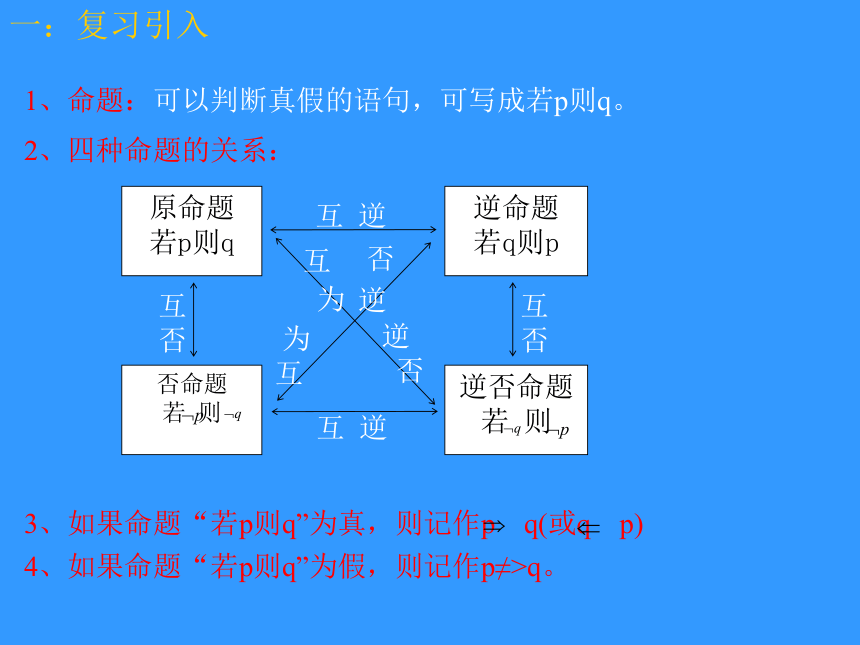
课件11张PPT。充分条件与必要条件制作者:冯英华 QQ:110124942一:复习引入4、如果命题“若p则q”为假,则记作p≠>q。 1、命题:可以判断真假的语句,可写成若p则q。2、四种命题的关系:3、如果命题“若p则q”为真,则记作p q(或q p)一、复习引入(4) p≠>q,q≠>p答 :5、例1、判断下列命题是真命题还是假命题,并研究其逆命题的
真假。
(1)若x=y,则x2=y2
(2)有两角相等的三角形是等腰三角形。
(3)ax2+ax+1>0的解集为R,则,0(4)若a2>b2,则a>b。
(1)p q,q≠>p(2) p q,q p (3) p≠>q,q p一:复习引入
6、在原命题中研究条件多结论的制约程度(1)若x=y,则x2=y2
(2)有两角相等的三角形是等腰三角形。
(3)ax2+ax+1>0的解集为R,则,0(4)若a2>b2,则a>b。在真命题(1)、(2)中,p足以导致q,也就是说条件充分了。
在假命题(3)、(4)中条件不充分。在真命题(2)、(3)中,p是q成立所必须具备的前提
在假命题(1)、(4)中,p不是q成立所必须具备的前提。二、新课2、从集合角度理解 定义2:如果已知q p,则说p是q的必要条件。如果已知p q且q≠>p,则说p是q的充分不必要条件。如果已知q p且p≠>q,则说p是q的必要不充分条件。 (1)p q,相当于 ,(2)q p,相当于 , 定义3:如果既有p q,又有q p,就记作p q,则说p是q的充要条件。1 、定义1:如果已知p q,则说p是q的充分条件。即:要使 成立,只要 就足够了即:为使 成立,必须要使 即:互为充要的两个条件刻划的是二、新课3、例1、判断下列命题中前者是后者的什么条件,后者是前者的什么条件?
(1)若x=y,则x2=y2
(2)有两角相等的三角形是等腰三角形。
(3)ax2+ax+1>0的解集为R,则,0(4)若a2>b2,则a>b。(4)既不充分也不必要 既不充分也不必要答:(1)充分不必要 必要不充分 (2)充要 充要(3)必要不充分 充分不必要 二、新课5、例2,判断下列问题中,p是q成立的什么条件?
p q
(1)x2>1 x<-1
(2)|x-2|<3 -x2+4x+5>0
(3)xy≠0 x≠0或y≠0 解:4、简化定义:如果已知p q,
则说p是q的充分条件,q是p的必要条件。(1)p≠> q,q p(2)p q(3)p q,q≠>p (原问题 x=0且y=0,则xy=0) 二、新课判别充要条件问题的6、判别步骤(1)可先简化命题。
(2)否定一个命题只要举出一个反例即可
(3)将命题转化为等价的逆否命题后再判断。(1)认清条件和结论。(2)考察p q和q p的真假二、新课8、例3、加入恰当的前提条件,使的下列成语满足充分性与必要性的四种形式。
(1)水滴石穿
(2)骄兵必败
(3)有志者事竞成
(4)头发长,见识短
(5)名师出高徒
(6)放下屠刀,立地成佛
(7)兔子尾巴长不了
(8)不到长城非好汉
(9)春回大地,万物复苏
(10)海内存知己
(11)蜡炬成灰泪始干
(12)玉不琢,不成器
三、小结3、判别步骤:(1)可先简化命题。(2)否定一个命题只要举出一个反例即可。(3)将命题转化为等价的 逆否命题后再判断。(1)认清条件和结论(2)考察p q和q p的真假1、定义1:如果已知p q,则说p是q的充分条件,q是p的必要条件。2、定义2:如果既有p q,又有q p,就记作p q,
则说p是q的充要条件。四、作业1、课本P36练习1、2。
补:2、写出生活中有四种关系的名言名句各一句
3、名句探微————名言名句充要关系之剖析
(字数不少于500)
真假。
(1)若x=y,则x2=y2
(2)有两角相等的三角形是等腰三角形。
(3)ax2+ax+1>0的解集为R,则,0
(1)p q,q≠>p(2) p q,q p (3) p≠>q,q p一:复习引入
6、在原命题中研究条件多结论的制约程度(1)若x=y,则x2=y2
(2)有两角相等的三角形是等腰三角形。
(3)ax2+ax+1>0的解集为R,则,0
在假命题(3)、(4)中条件不充分。在真命题(2)、(3)中,p是q成立所必须具备的前提
在假命题(1)、(4)中,p不是q成立所必须具备的前提。二、新课2、从集合角度理解 定义2:如果已知q p,则说p是q的必要条件。如果已知p q且q≠>p,则说p是q的充分不必要条件。如果已知q p且p≠>q,则说p是q的必要不充分条件。 (1)p q,相当于 ,(2)q p,相当于 , 定义3:如果既有p q,又有q p,就记作p q,则说p是q的充要条件。1 、定义1:如果已知p q,则说p是q的充分条件。即:要使 成立,只要 就足够了即:为使 成立,必须要使 即:互为充要的两个条件刻划的是二、新课3、例1、判断下列命题中前者是后者的什么条件,后者是前者的什么条件?
(1)若x=y,则x2=y2
(2)有两角相等的三角形是等腰三角形。
(3)ax2+ax+1>0的解集为R,则,0
p q
(1)x2>1 x<-1
(2)|x-2|<3 -x2+4x+5>0
(3)xy≠0 x≠0或y≠0 解:4、简化定义:如果已知p q,
则说p是q的充分条件,q是p的必要条件。(1)p≠> q,q p(2)p q(3)p q,q≠>p (原问题 x=0且y=0,则xy=0) 二、新课判别充要条件问题的6、判别步骤(1)可先简化命题。
(2)否定一个命题只要举出一个反例即可
(3)将命题转化为等价的逆否命题后再判断。(1)认清条件和结论。(2)考察p q和q p的真假二、新课8、例3、加入恰当的前提条件,使的下列成语满足充分性与必要性的四种形式。
(1)水滴石穿
(2)骄兵必败
(3)有志者事竞成
(4)头发长,见识短
(5)名师出高徒
(6)放下屠刀,立地成佛
(7)兔子尾巴长不了
(8)不到长城非好汉
(9)春回大地,万物复苏
(10)海内存知己
(11)蜡炬成灰泪始干
(12)玉不琢,不成器
三、小结3、判别步骤:(1)可先简化命题。(2)否定一个命题只要举出一个反例即可。(3)将命题转化为等价的 逆否命题后再判断。(1)认清条件和结论(2)考察p q和q p的真假1、定义1:如果已知p q,则说p是q的充分条件,q是p的必要条件。2、定义2:如果既有p q,又有q p,就记作p q,
则说p是q的充要条件。四、作业1、课本P36练习1、2。
补:2、写出生活中有四种关系的名言名句各一句
3、名句探微————名言名句充要关系之剖析
(字数不少于500)
