充要条件[上学期]
图片预览





文档简介
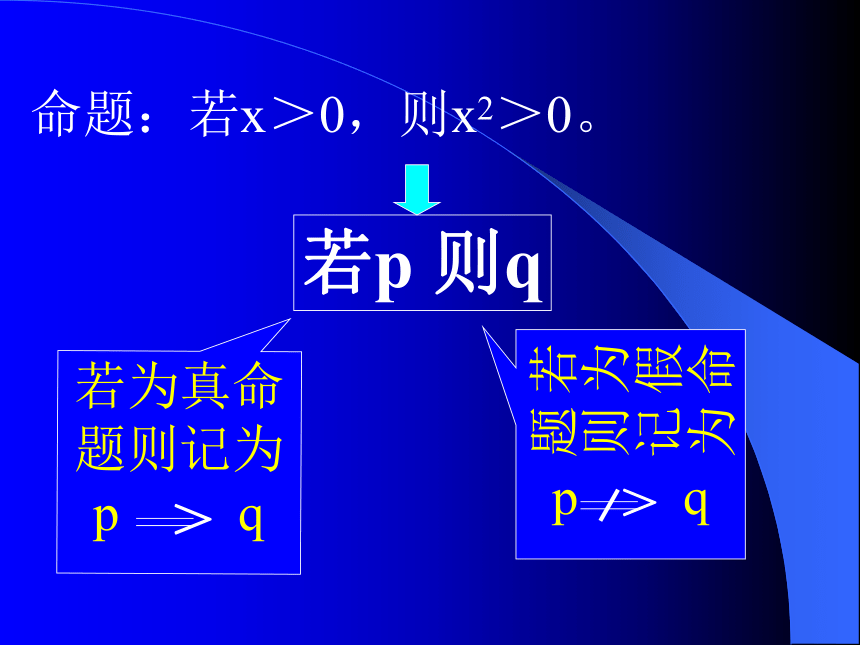
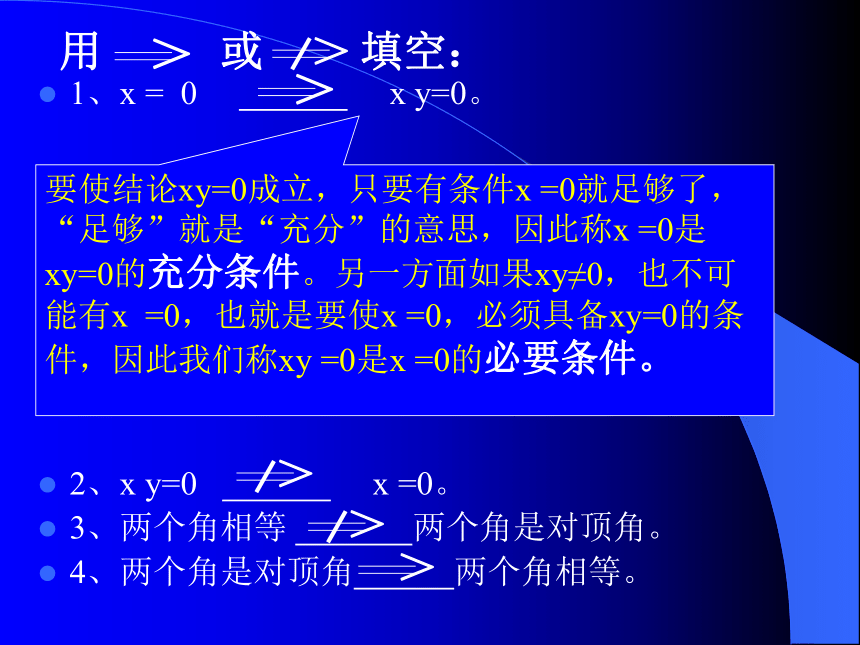
课件18张PPT。充分条件与必要条件命题:若x>0,则x2>0。若p 则q1、x = 0 x y=0。
2、x y=0 x =0。
3、两个角相等 两个角是对顶角。
4、两个角是对顶角 两个角相等。要使结论xy=0成立,只要有条件x =0就足够了,“足够”就是“充分”的意思,因此称x =0是xy=0的充分条件。另一方面如果xy≠0,也不可能有x =0,也就是要使x =0,必须具备xy=0的条件,因此我们称xy =0是x =0的必要条件。
变式训练:(1)a>b a+c>b+c;(2)a2-2ab+b2=0 a=b;(3)四边相等的四边形 正方形。2、填空:(1)x2=y2是x=y的 条件。(2)对角线互相平分的四边形是矩形的 条件。必要条件必要条件 则“两个三角形全等” 是“两个三角形的面积相等”的充分条件,“两个三角形的面积相等”是“两个三角形全等”的必要条件。例如:由x>0则“x>0”是 “x2>0”的充分条件,
“x2>0”是 “x>0”的必要条件;x2>0,由两个三角形全等两个三角形的面积相等,考察命题:
p:三角形的三条边相等
q:三角形的三个角相等因为pq,所以p是q的充分条件,又因为qp,所以p是q的必要条件, 我们称“三角形三条边相等”是“三角形三
个角相等”的充分必要条件,简称充要条件。分析:定义:一般地,q,又有qp,如果既有p记为pq, 这时,p既是q的充分条件,又是q的必要条件,称p是q的充分必要条件,简称充要条件。思考1:当p是q的充要条件时,q是p的充要条件吗?为什么?说明 3:下列各题中p是q的什么条件?充分不必要条件必要不充分条件充要条件既不充分又不必要条件例2、判断下列命题中前者是后者的什么条件? 后者是前者的什么条件? (1)若x=y,则x2=y2。 (2)有两角相等的三角形是等腰三角形。 (3)ax2+ax+1>0的解集为R,则0b2,则a>b。答:前者是后者的充分不必要条件。前者是后者的充要条件。前者是后者的必要不充分条件。前者是后者的既不充分也不必要条件。简化定义:指出下列各组命题中,p是q的什么条件,
(4)p:x = y ;q:x2 = y2。
(5)p:三角形的三条边相等;
q:三角形的三个角相等。
(6)p: (x-2) (x-1) = 0
q:x = 1解:充分不必要条件必要不充分条件充要条件变式2:用“充分而不必要条件”、 “必要而不充分条件”、 “充要条件” 、“既不充分又不必要条件”填空:
(1)“a、b是偶数”是“a+b是偶数”的 。
(2) “ab>0”是“a、b都是负数”的 。
(3)“两个三角形的面积相等”是“这两个三角形全等”的 。 充分不必要条件必要不充分条件必要不充分条件变式3:用“充分而不必要条件”、 “必要而不充分条件”、 “充要条件” 、“既不充分又不必要条件”填空:1、“x是6的倍数”是“x是2的倍数”的 。2、“x是2的倍数”是“x是6的倍数”的 。3、“x是2的倍数也是3的倍数”是“x是6的倍数” 的 。4、“x是4的倍数”是“x是6的倍数”的 。5、“(x-2)(x-3)=0”是“x-2=0”的 。6、“同位角相等”是“两直线平行”的 。7、“x=3”是“x2=9”的 。8、“四边形的对角线相等”是“四边形是平行四边形”
的 。充分而不必要条件充分而不必要条件必要而不充分条件必要而不充分条件充要条件充要条件既不充分又不必要条件既不充分又不必要条件变式4:用“充分而不必要条件”、 “必要而不充分条件”、 “充要条件” 、“既不充分又不必要条件”填空:
(1)p: 2﹤x ﹤3. q: 1﹤x ﹤4.
p是q的 。
(2) p: -2﹤x ﹤1. q: -1 ≤ x ﹤0.
p是q的 。
(3) p: ∣3x-1∣﹥ 2. q: ∣2x-5∣≤ 1
p是q的 。
(4) p: x﹥ 2. q: ∣2x-5∣≤ 1
p是q的 ______。
充分不必要条件必要不充分条件必要不充分条件 既不充分又不必要条件小结1:小结2:
1、充分而不必要条件的判定方法:2、必要而不充分条件的判定方法:3、充要条件的判定方法:小结3: ① 认清条件和结论。① 可先简化命题。③ 将命题转化为等价的逆否命题后再判断。② 否定一个命题只要举出一个反例即可。1、定义1:
2、x y=0 x =0。
3、两个角相等 两个角是对顶角。
4、两个角是对顶角 两个角相等。要使结论xy=0成立,只要有条件x =0就足够了,“足够”就是“充分”的意思,因此称x =0是xy=0的充分条件。另一方面如果xy≠0,也不可能有x =0,也就是要使x =0,必须具备xy=0的条件,因此我们称xy =0是x =0的必要条件。
变式训练:(1)a>b a+c>b+c;(2)a2-2ab+b2=0 a=b;(3)四边相等的四边形 正方形。2、填空:(1)x2=y2是x=y的 条件。(2)对角线互相平分的四边形是矩形的 条件。必要条件必要条件 则“两个三角形全等” 是“两个三角形的面积相等”的充分条件,“两个三角形的面积相等”是“两个三角形全等”的必要条件。例如:由x>0则“x>0”是 “x2>0”的充分条件,
“x2>0”是 “x>0”的必要条件;x2>0,由两个三角形全等两个三角形的面积相等,考察命题:
p:三角形的三条边相等
q:三角形的三个角相等因为pq,所以p是q的充分条件,又因为qp,所以p是q的必要条件, 我们称“三角形三条边相等”是“三角形三
个角相等”的充分必要条件,简称充要条件。分析:定义:一般地,q,又有qp,如果既有p记为pq, 这时,p既是q的充分条件,又是q的必要条件,称p是q的充分必要条件,简称充要条件。思考1:当p是q的充要条件时,q是p的充要条件吗?为什么?说明 3:下列各题中p是q的什么条件?充分不必要条件必要不充分条件充要条件既不充分又不必要条件例2、判断下列命题中前者是后者的什么条件? 后者是前者的什么条件? (1)若x=y,则x2=y2。 (2)有两角相等的三角形是等腰三角形。 (3)ax2+ax+1>0的解集为R,则0
(4)p:x = y ;q:x2 = y2。
(5)p:三角形的三条边相等;
q:三角形的三个角相等。
(6)p: (x-2) (x-1) = 0
q:x = 1解:充分不必要条件必要不充分条件充要条件变式2:用“充分而不必要条件”、 “必要而不充分条件”、 “充要条件” 、“既不充分又不必要条件”填空:
(1)“a、b是偶数”是“a+b是偶数”的 。
(2) “ab>0”是“a、b都是负数”的 。
(3)“两个三角形的面积相等”是“这两个三角形全等”的 。 充分不必要条件必要不充分条件必要不充分条件变式3:用“充分而不必要条件”、 “必要而不充分条件”、 “充要条件” 、“既不充分又不必要条件”填空:1、“x是6的倍数”是“x是2的倍数”的 。2、“x是2的倍数”是“x是6的倍数”的 。3、“x是2的倍数也是3的倍数”是“x是6的倍数” 的 。4、“x是4的倍数”是“x是6的倍数”的 。5、“(x-2)(x-3)=0”是“x-2=0”的 。6、“同位角相等”是“两直线平行”的 。7、“x=3”是“x2=9”的 。8、“四边形的对角线相等”是“四边形是平行四边形”
的 。充分而不必要条件充分而不必要条件必要而不充分条件必要而不充分条件充要条件充要条件既不充分又不必要条件既不充分又不必要条件变式4:用“充分而不必要条件”、 “必要而不充分条件”、 “充要条件” 、“既不充分又不必要条件”填空:
(1)p: 2﹤x ﹤3. q: 1﹤x ﹤4.
p是q的 。
(2) p: -2﹤x ﹤1. q: -1 ≤ x ﹤0.
p是q的 。
(3) p: ∣3x-1∣﹥ 2. q: ∣2x-5∣≤ 1
p是q的 。
(4) p: x﹥ 2. q: ∣2x-5∣≤ 1
p是q的 ______。
充分不必要条件必要不充分条件必要不充分条件 既不充分又不必要条件小结1:小结2:
1、充分而不必要条件的判定方法:2、必要而不充分条件的判定方法:3、充要条件的判定方法:小结3: ① 认清条件和结论。① 可先简化命题。③ 将命题转化为等价的逆否命题后再判断。② 否定一个命题只要举出一个反例即可。1、定义1:
