人教版2023年七年级(下) 5.1相交线 同步练习(word解析版)
文档属性
| 名称 | 人教版2023年七年级(下) 5.1相交线 同步练习(word解析版) |
|
|
| 格式 | docx | ||
| 文件大小 | 259.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-28 15:39:48 | ||
图片预览


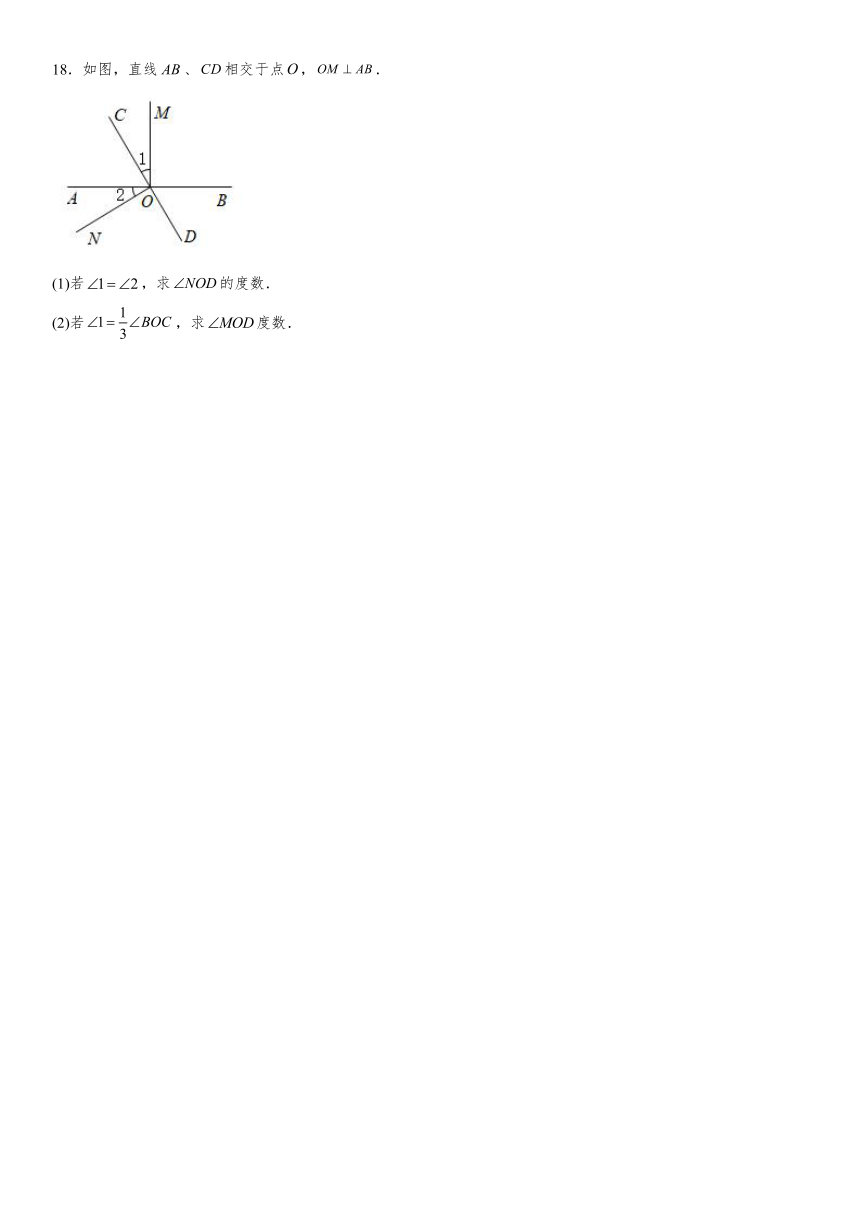
文档简介
人教版2023年七年级(下) 5.1相交线 同步练习
一、选择题
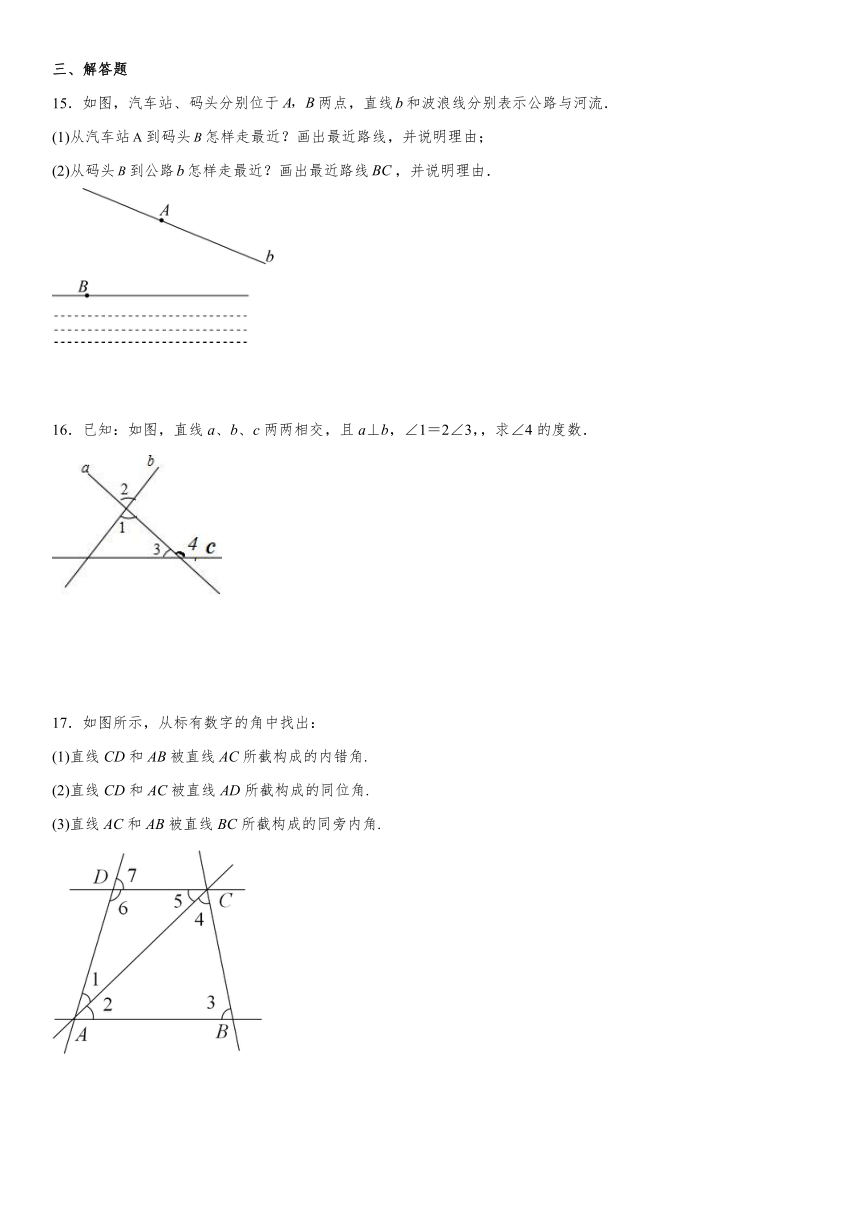
1.以下四个图中有直线、射线、线段,其中能相交的是( )
A.①②③④ B.①③ C.②③④ D.①
2.下列四个图形中,和是对顶角的是( ).
A.B.C. D.
3.下列图形中,∠1与∠2是邻补角的是( )
A. B. C. D.
4.如图,从位置O到直线公路l有四条小道,其中路程最短的是( )
A.OA B.OB C.OC D.OD
5.下列各图中,与是同位角的是( )
A. B. C. D.
6.若,则的邻补角是( )
A. B. C. D.
7.如图,O是上一点,于点O,直线经过O点,,则的度数为( )
A.100° B.105° C.115° D.125°
8.如图,下列判断正确的是( )
A.与是同旁内角 B.与是同位角
C.与是对顶角 D.与是内错角
二、填空题
9.垂直是相交的一种特殊情形,两条直线互相垂直,其中的一条直线叫做另一条直线的______,它们的交点叫做______.
10.如果两个角有一个公共顶点,并且其中一个角的两边是另一个角的两边的___________,那么这两个角互为对顶角.图中∠1的对顶角是______.
11.与是对顶角,与是邻补角,则________度.
12.如图,直线AB与CD相交于点O,∠BOC+∠AOD=288°,那么∠BOC的邻补角是_____度.
13.如图,∠2的同旁内角是_____.
14.如图,直线a,b被直线c所截,则形成的角中与∠1互为内错角的是______.
三、解答题
15.如图,汽车站、码头分别位于两点,直线和波浪线分别表示公路与河流.
(1)从汽车站到码头怎样走最近?画出最近路线,并说明理由;
(2)从码头到公路怎样走最近?画出最近路线,并说明理由.
16.已知:如图,直线a、b、c两两相交,且a⊥b,∠1=2∠3,,求∠4的度数.
17.如图所示,从标有数字的角中找出:
(1)直线CD和AB被直线AC所截构成的内错角.
(2)直线CD和AC被直线AD所截构成的同位角.
(3)直线AC和AB被直线BC所截构成的同旁内角.
18.如图,直线、相交于点,.
(1)若,求的度数.
(2)若,求度数.
参考答案
1.B
【分析】根据直线可以沿着两个方向延伸,射线可以沿着一个方向延伸,线段不能延伸依次判断即可.
【详解】解:①射线和直线延伸后可以相交,符合题意;
②线段不能向两端延伸,不能相交,不符合题意;
③两条直线延伸后可以相交,符合题意;
④射线和直线延伸后不能相交,不符合题意;
故选:B.
【点睛】题目主要考查直线、线段及射线的知识,掌握直线可以沿着两个方向延伸,射线可以沿着一个方向延伸,线段不能延伸是解题关键.
2.D
【分析】根据对顶角的定义,对顶角:有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角,据此即可判断.
【详解】解: A、两角只有一条边互为反向延长线,另一条边没有互为反向延长线,不符合题意;
B、两角没有公共顶点,两角也是只有一条边互为反向延长线,另一条边没有互为反向延长线,不符合题意;
C、两角只有一条边互为反向延长线,另一条边没有互为反向延长线,不符合题意;
D、两角有一个公共顶点,并且一个角的两边是另一个角两边的反向延长线的两个角,符合题意;
故选:D.
【点睛】本题考查了对顶角的定义,属于基础题,熟练掌握对顶角的概念是解决本题的关键.
3.A
【分析】根据邻补角的概念进行判定即可得出答案.
【详解】解:A.因为∠1与∠2是邻补角,故A选项符合题意;
B.因为∠1与∠2有公共顶点且两边互为延长线,所以B选项∠1与∠2是对顶角,故B选项不符合题意;
C.因为∠1与∠2的和显然不是180°,所以∠1与∠2不是邻补角,故C选项不符合题意;
D.因为∠1与∠2不相邻、不互补,所以∠1与∠2不是邻补角,故D选项不符合题意;
故选:A.
【点睛】本题考查的是邻补角的定义,解题关键是明白定义的本质,一是相邻,二是互补.
4.C
【分析】根据垂线的性质即可得到结论.
【详解】解:根据垂线段最短得,能最快到达公路l的小道是OC,
故选C.
【点睛】本题考查了垂线段最短,熟记垂线的性质是解题的关键.
5.B
【分析】根据同位角的意义,结合图形进行判断即可.
【详解】解:A.选项中的两个角不是两条直线被一条直线所截出现的角,不符合题意;
B.选项中的两个角符合同位角的意义,符合题意;
C.选项中的两个角不是两条直线被一条直线所截出现的角,不符合题意;
D.选项中的两个角不是两条直线被一条直线所截出现的角,不符合题意;
故选:B.选项
【点睛】本题考查了同位角、内错角、同旁内角,判断是否是同位角,必须符合三线八角中,在截线的同侧,并且在被截线的同一方的两个角是同位角.
6.B
【分析】根据邻补角的和是进行求解即可.
【详解】解:∵,
∴的邻补角为,
故选:B.
【点睛】此题考查了邻补角,熟练掌握邻补角的和为是解题的关键.
7.C
【分析】由,可得,由对顶角相等可得,根据角的和差即可解答.
【详解】解:∵,
∴,
∵,
∴.
故选:C.
【点睛】此题考查垂直的定义以及对顶角,题目很简单,解题时要仔细识图.
8.A
【分析】根据同位角、同旁内角、内错角和对顶角的概念解答即可.
【详解】解:A、与是同旁内角,故本选项符合题意;
B、与不是同位角,故本选项不合题意;
C、与不是对顶角,故本选项不合题意;
D、与不是内错角,故本选项不合题意;
故选:A.
【点睛】本题考查了同位角、内错角、同旁内角的定义,两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角;两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角;两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角.
9. 垂线 垂足
【解析】略
10. 反向延长线 ∠1
【解析】略
11.
【分析】根据对顶角相等,邻补角互补即可得到答案.
【详解】解:由题意可得,
,,
∴,
故答案为.
【点睛】本题考查对顶角相等,邻补角互补,解题的关键是根据题意得到角度关系.
12.36
【分析】先根据对顶角相等求出∠BOC的度数,再利用邻补角的和等于180°列式计算即可.
【详解】解:∵∠BOC+∠AOD=288°,∠BOC=∠AOD,
∴∠BOC=×288°=144°,
∴∠BOC的邻补角=180°﹣144°=36°.
故答案为:36.
【点睛】本题主要考查了对顶角相等,邻补角互补的性质,是基础题,比较简单,熟知相关知识是解题的关键.
13.∠4
【分析】根据同旁内角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角进行分析即可.
【详解】解:∠2的同旁内角是∠4,
故答案为:∠4.
【点睛】此题主要考查了同旁内角的概念,关键是掌握同旁内角的边构成“U”形.
14.∠4
【分析】根据内错角的概念判断即可.
【详解】∵直线a、b被直线c所截,
∴∠1与∠4是内错角.
故答案为:∠4.
【点睛】本题考查了内错角,内错角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角,掌握内错角的概念是解题的关键.
15.(1)作图见解析,理由见解析
(2)作图见解析,理由见解析
【分析】(1)根据两点之间线段最短解决问题.
(2)根据垂线段最短解决问题.
【详解】(1)解:如图,连接,线段即为所求作.
(2)如图,过点作于点,线段即为所求作.
【点睛】本题考查作图﹣应用与设计作图,垂线段最短,两点之间线段最短等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
16.135°
【分析】根据垂直和邻补角的性质求解即可.
【详解】解:∵a⊥b
∴∠2=∠1=90°
又∵∠1=2∠3,
∴90°=2∠3,
∴∠3=45°
又∠3与∠4互为邻补角,
所以∠3+∠4=180°,即45°+∠4=180°
所以∠4=135°
【点睛】此题考查了垂直和邻补角的性质,解题的关键是掌握垂直和邻补角的有关性质
17.(1)直线CD和AB被直线AC所截构成的内错角是∠2和∠5; (2)直线CD和AC被直线AD所截构成的同位角是∠1和∠7;(3)直线AC和AB被直线BC所截构成的同旁内角是∠3和∠4
【分析】根据两条直线被第三条直线所截,所形成的角中,两角在两条直线的中间,第三条直线的两旁,可得内错角,两角在两直线的中间,第三条直线的同侧,可得同旁内角,两角在两条直线的同侧,第三条直线的同侧,可得同位角.
【详解】解:(1)直线CD和AB被直线AC所截构成的内错角是∠2和∠5.
(2)直线CD和AC被直线AD所截构成的同位角是∠1和∠7.
(3)直线AC和AB被直线BC所截构成的同旁内角是∠3和∠4.
【点睛】此题主要考查了三线八角,关键是掌握同位角的边构成F形,内错角的边构成Z形,同旁内角的边构成U形.
18.(1)
(2)
【分析】(1)根据垂直的定义可得,再求出,然后根据平角等于求解;
(2)根据垂直的定义可得,列方程求出,再根据余角和邻补角的定义求解.
【详解】(1)解:∵,
∴,
∵,
∴,
∴
(2)解:∵,
∴,
∵,
∴,
∴
∴
答:的度数是.
【点睛】本题考查了垂线的定义,邻补角的定义,掌握概念并准确识图,找准各角之间的关系是解题的关键.
一、选择题
1.以下四个图中有直线、射线、线段,其中能相交的是( )
A.①②③④ B.①③ C.②③④ D.①
2.下列四个图形中,和是对顶角的是( ).
A.B.C. D.
3.下列图形中,∠1与∠2是邻补角的是( )
A. B. C. D.
4.如图,从位置O到直线公路l有四条小道,其中路程最短的是( )
A.OA B.OB C.OC D.OD
5.下列各图中,与是同位角的是( )
A. B. C. D.
6.若,则的邻补角是( )
A. B. C. D.
7.如图,O是上一点,于点O,直线经过O点,,则的度数为( )
A.100° B.105° C.115° D.125°
8.如图,下列判断正确的是( )
A.与是同旁内角 B.与是同位角
C.与是对顶角 D.与是内错角
二、填空题
9.垂直是相交的一种特殊情形,两条直线互相垂直,其中的一条直线叫做另一条直线的______,它们的交点叫做______.
10.如果两个角有一个公共顶点,并且其中一个角的两边是另一个角的两边的___________,那么这两个角互为对顶角.图中∠1的对顶角是______.
11.与是对顶角,与是邻补角,则________度.
12.如图,直线AB与CD相交于点O,∠BOC+∠AOD=288°,那么∠BOC的邻补角是_____度.
13.如图,∠2的同旁内角是_____.
14.如图,直线a,b被直线c所截,则形成的角中与∠1互为内错角的是______.
三、解答题
15.如图,汽车站、码头分别位于两点,直线和波浪线分别表示公路与河流.
(1)从汽车站到码头怎样走最近?画出最近路线,并说明理由;
(2)从码头到公路怎样走最近?画出最近路线,并说明理由.
16.已知:如图,直线a、b、c两两相交,且a⊥b,∠1=2∠3,,求∠4的度数.
17.如图所示,从标有数字的角中找出:
(1)直线CD和AB被直线AC所截构成的内错角.
(2)直线CD和AC被直线AD所截构成的同位角.
(3)直线AC和AB被直线BC所截构成的同旁内角.
18.如图,直线、相交于点,.
(1)若,求的度数.
(2)若,求度数.
参考答案
1.B
【分析】根据直线可以沿着两个方向延伸,射线可以沿着一个方向延伸,线段不能延伸依次判断即可.
【详解】解:①射线和直线延伸后可以相交,符合题意;
②线段不能向两端延伸,不能相交,不符合题意;
③两条直线延伸后可以相交,符合题意;
④射线和直线延伸后不能相交,不符合题意;
故选:B.
【点睛】题目主要考查直线、线段及射线的知识,掌握直线可以沿着两个方向延伸,射线可以沿着一个方向延伸,线段不能延伸是解题关键.
2.D
【分析】根据对顶角的定义,对顶角:有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角,据此即可判断.
【详解】解: A、两角只有一条边互为反向延长线,另一条边没有互为反向延长线,不符合题意;
B、两角没有公共顶点,两角也是只有一条边互为反向延长线,另一条边没有互为反向延长线,不符合题意;
C、两角只有一条边互为反向延长线,另一条边没有互为反向延长线,不符合题意;
D、两角有一个公共顶点,并且一个角的两边是另一个角两边的反向延长线的两个角,符合题意;
故选:D.
【点睛】本题考查了对顶角的定义,属于基础题,熟练掌握对顶角的概念是解决本题的关键.
3.A
【分析】根据邻补角的概念进行判定即可得出答案.
【详解】解:A.因为∠1与∠2是邻补角,故A选项符合题意;
B.因为∠1与∠2有公共顶点且两边互为延长线,所以B选项∠1与∠2是对顶角,故B选项不符合题意;
C.因为∠1与∠2的和显然不是180°,所以∠1与∠2不是邻补角,故C选项不符合题意;
D.因为∠1与∠2不相邻、不互补,所以∠1与∠2不是邻补角,故D选项不符合题意;
故选:A.
【点睛】本题考查的是邻补角的定义,解题关键是明白定义的本质,一是相邻,二是互补.
4.C
【分析】根据垂线的性质即可得到结论.
【详解】解:根据垂线段最短得,能最快到达公路l的小道是OC,
故选C.
【点睛】本题考查了垂线段最短,熟记垂线的性质是解题的关键.
5.B
【分析】根据同位角的意义,结合图形进行判断即可.
【详解】解:A.选项中的两个角不是两条直线被一条直线所截出现的角,不符合题意;
B.选项中的两个角符合同位角的意义,符合题意;
C.选项中的两个角不是两条直线被一条直线所截出现的角,不符合题意;
D.选项中的两个角不是两条直线被一条直线所截出现的角,不符合题意;
故选:B.选项
【点睛】本题考查了同位角、内错角、同旁内角,判断是否是同位角,必须符合三线八角中,在截线的同侧,并且在被截线的同一方的两个角是同位角.
6.B
【分析】根据邻补角的和是进行求解即可.
【详解】解:∵,
∴的邻补角为,
故选:B.
【点睛】此题考查了邻补角,熟练掌握邻补角的和为是解题的关键.
7.C
【分析】由,可得,由对顶角相等可得,根据角的和差即可解答.
【详解】解:∵,
∴,
∵,
∴.
故选:C.
【点睛】此题考查垂直的定义以及对顶角,题目很简单,解题时要仔细识图.
8.A
【分析】根据同位角、同旁内角、内错角和对顶角的概念解答即可.
【详解】解:A、与是同旁内角,故本选项符合题意;
B、与不是同位角,故本选项不合题意;
C、与不是对顶角,故本选项不合题意;
D、与不是内错角,故本选项不合题意;
故选:A.
【点睛】本题考查了同位角、内错角、同旁内角的定义,两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角;两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角;两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角.
9. 垂线 垂足
【解析】略
10. 反向延长线 ∠1
【解析】略
11.
【分析】根据对顶角相等,邻补角互补即可得到答案.
【详解】解:由题意可得,
,,
∴,
故答案为.
【点睛】本题考查对顶角相等,邻补角互补,解题的关键是根据题意得到角度关系.
12.36
【分析】先根据对顶角相等求出∠BOC的度数,再利用邻补角的和等于180°列式计算即可.
【详解】解:∵∠BOC+∠AOD=288°,∠BOC=∠AOD,
∴∠BOC=×288°=144°,
∴∠BOC的邻补角=180°﹣144°=36°.
故答案为:36.
【点睛】本题主要考查了对顶角相等,邻补角互补的性质,是基础题,比较简单,熟知相关知识是解题的关键.
13.∠4
【分析】根据同旁内角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角进行分析即可.
【详解】解:∠2的同旁内角是∠4,
故答案为:∠4.
【点睛】此题主要考查了同旁内角的概念,关键是掌握同旁内角的边构成“U”形.
14.∠4
【分析】根据内错角的概念判断即可.
【详解】∵直线a、b被直线c所截,
∴∠1与∠4是内错角.
故答案为:∠4.
【点睛】本题考查了内错角,内错角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角,掌握内错角的概念是解题的关键.
15.(1)作图见解析,理由见解析
(2)作图见解析,理由见解析
【分析】(1)根据两点之间线段最短解决问题.
(2)根据垂线段最短解决问题.
【详解】(1)解:如图,连接,线段即为所求作.
(2)如图,过点作于点,线段即为所求作.
【点睛】本题考查作图﹣应用与设计作图,垂线段最短,两点之间线段最短等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
16.135°
【分析】根据垂直和邻补角的性质求解即可.
【详解】解:∵a⊥b
∴∠2=∠1=90°
又∵∠1=2∠3,
∴90°=2∠3,
∴∠3=45°
又∠3与∠4互为邻补角,
所以∠3+∠4=180°,即45°+∠4=180°
所以∠4=135°
【点睛】此题考查了垂直和邻补角的性质,解题的关键是掌握垂直和邻补角的有关性质
17.(1)直线CD和AB被直线AC所截构成的内错角是∠2和∠5; (2)直线CD和AC被直线AD所截构成的同位角是∠1和∠7;(3)直线AC和AB被直线BC所截构成的同旁内角是∠3和∠4
【分析】根据两条直线被第三条直线所截,所形成的角中,两角在两条直线的中间,第三条直线的两旁,可得内错角,两角在两直线的中间,第三条直线的同侧,可得同旁内角,两角在两条直线的同侧,第三条直线的同侧,可得同位角.
【详解】解:(1)直线CD和AB被直线AC所截构成的内错角是∠2和∠5.
(2)直线CD和AC被直线AD所截构成的同位角是∠1和∠7.
(3)直线AC和AB被直线BC所截构成的同旁内角是∠3和∠4.
【点睛】此题主要考查了三线八角,关键是掌握同位角的边构成F形,内错角的边构成Z形,同旁内角的边构成U形.
18.(1)
(2)
【分析】(1)根据垂直的定义可得,再求出,然后根据平角等于求解;
(2)根据垂直的定义可得,列方程求出,再根据余角和邻补角的定义求解.
【详解】(1)解:∵,
∴,
∵,
∴,
∴
(2)解:∵,
∴,
∵,
∴,
∴
∴
答:的度数是.
【点睛】本题考查了垂线的定义,邻补角的定义,掌握概念并准确识图,找准各角之间的关系是解题的关键.
