充要条件[上学期]
图片预览





文档简介
课件12张PPT。E—mail:zqxiahn@163.com
1.8 充分条件和必要条件
主讲人:李新华
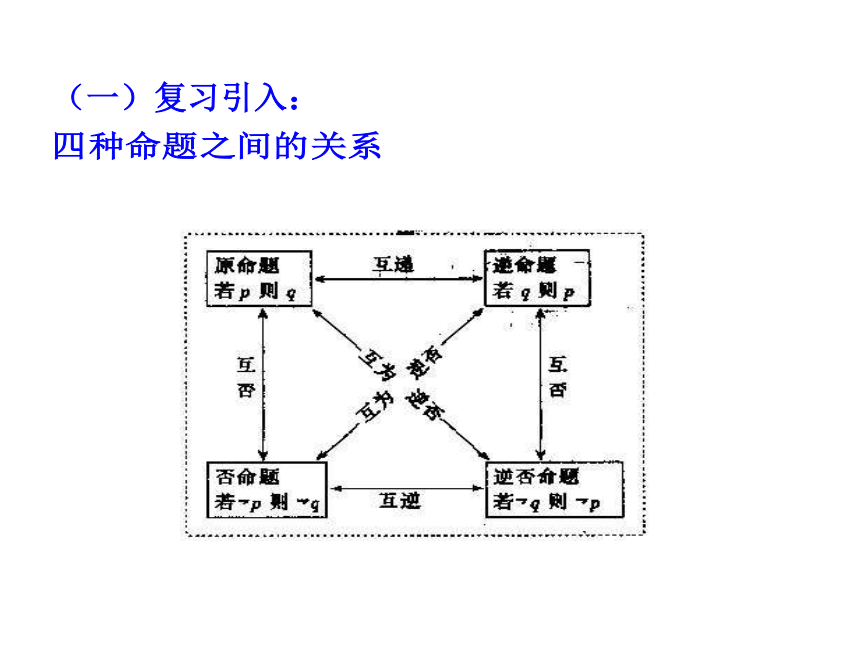
新野一高2005年9月(一)复习引入:问题:
试写出下面命题的逆命题、否命题和逆否命题,并判断真假。
“若x>1,则x2>1”.逆否命题:若x2 ≤ 1 , 则x ≤ 1.逆命题:若x2>1 ,则x>1;否命题:若x≤1 ,则x2≤1;假命题假命题真命题(二 )概念: 一般地,如果已知 那么我们说,p 是 q的充分条件, q是p 的必要条件.1.8 充分条件和必要条件 例如:指出下列各组命题中,p是q的什么条件,q是p的什么条件: p:x≠y;q:x2≠y2.
P:x>0;q:x2>0 .
P:三角形的三个角相等;
q:三角形的三条边相等。
P:两个三角形全等;q:两个三角形的面积相等。 一般地,如果既有 又有 , 就记作
这时,p既是q 的充分条件,又是q的必要条件,我们就说,p 是 q的充分必要条件, 简称充要条件。例如,
“x是6的倍数”是“x是2的倍数”的————————;
“x是2的倍数”是 “x是6的倍数”的————————;
“x既是2的倍数也是3的倍数”是“x是6的倍数”的————;
“x是4的倍数”是“x是6的倍数”的 ——————————。充分而不必要条件必要而不充分条件充要条件既不充分也不必要条件(三)例题:必要而不充分条件充要条件充分而不必要条件既不充分也不必要条件 判断时要先认准条件与结论,再判定“若p则q”和“若q则p”的真假,指出充分和必要。充分而不必要条件例2 指出下列命题中p是q的什么条件? P:|x|≠3 q:x≠3(四)课堂练习1. 从“ ”、“ ”与“ ”中选出适当的符号填空:
(1)x>-1___x>1;
(2)x2=3x+4___x= ;
(3)两个角是对顶角________两个角相等;
(4)a=b____a+c=b+c.
2. 从“充分而不必要的条件”、“必要而不充分的条件”与“充要条件”中选出适当的一种填空:
(1) “两三角形全等” 是“两三角形相似”的------------------------------;
(2) “a=b”是 “ac=bc”的------------------------------;
(3) “a≠0”是 “ab ≠ 0”的-------------------------------.
(4) “四边形的两条对角线相等”是“四边形是矩形”的----------------------------.必要而不充分的条件充分而不必要的条件必要而不充分的条件必要而不充分的条件判断下列命题的真假:(1) “a>b” 是 “a2>b2”的充分条件;
(2) “a>b” 是 “a2>b2”的必要条件;
(3) “a>b” 是 “ac2>bc2”的充分条件;
(4) “a>b” 是 “a+c>b+c”的充要条件;真命题假命题假命题假命题4. 若p 是 的充分不必要条件,则 q 是 的———.充分不必要条件真真假假二判定方法:
(1) 判断时要先认准条件与结论,再判定“若p则q”和“若q则p”的真假,指出充分或必要。
(五)小结一 几个重要概念:
充分而不必要条件充要条件必要而不充分条件既不充分也不必要条件在今后判断p是q的什么条件时主要是指(2)利用互为逆否的命题是等价的命题进行转化:
“ ” “ ”必要条件充分条件充要条件思考题:
关于x的方程ax2+bx+c=0一个根为1的充分且必
要条件是------------。(六)布置作业:
教材 P36 1
P42 11、 12 、13
谢谢!再见
1.8 充分条件和必要条件
主讲人:李新华
新野一高2005年9月(一)复习引入:问题:
试写出下面命题的逆命题、否命题和逆否命题,并判断真假。
“若x>1,则x2>1”.逆否命题:若x2 ≤ 1 , 则x ≤ 1.逆命题:若x2>1 ,则x>1;否命题:若x≤1 ,则x2≤1;假命题假命题真命题(二 )概念: 一般地,如果已知 那么我们说,p 是 q的充分条件, q是p 的必要条件.1.8 充分条件和必要条件 例如:指出下列各组命题中,p是q的什么条件,q是p的什么条件: p:x≠y;q:x2≠y2.
P:x>0;q:x2>0 .
P:三角形的三个角相等;
q:三角形的三条边相等。
P:两个三角形全等;q:两个三角形的面积相等。 一般地,如果既有 又有 , 就记作
这时,p既是q 的充分条件,又是q的必要条件,我们就说,p 是 q的充分必要条件, 简称充要条件。例如,
“x是6的倍数”是“x是2的倍数”的————————;
“x是2的倍数”是 “x是6的倍数”的————————;
“x既是2的倍数也是3的倍数”是“x是6的倍数”的————;
“x是4的倍数”是“x是6的倍数”的 ——————————。充分而不必要条件必要而不充分条件充要条件既不充分也不必要条件(三)例题:必要而不充分条件充要条件充分而不必要条件既不充分也不必要条件 判断时要先认准条件与结论,再判定“若p则q”和“若q则p”的真假,指出充分和必要。充分而不必要条件例2 指出下列命题中p是q的什么条件? P:|x|≠3 q:x≠3(四)课堂练习1. 从“ ”、“ ”与“ ”中选出适当的符号填空:
(1)x>-1___x>1;
(2)x2=3x+4___x= ;
(3)两个角是对顶角________两个角相等;
(4)a=b____a+c=b+c.
2. 从“充分而不必要的条件”、“必要而不充分的条件”与“充要条件”中选出适当的一种填空:
(1) “两三角形全等” 是“两三角形相似”的------------------------------;
(2) “a=b”是 “ac=bc”的------------------------------;
(3) “a≠0”是 “ab ≠ 0”的-------------------------------.
(4) “四边形的两条对角线相等”是“四边形是矩形”的----------------------------.必要而不充分的条件充分而不必要的条件必要而不充分的条件必要而不充分的条件判断下列命题的真假:(1) “a>b” 是 “a2>b2”的充分条件;
(2) “a>b” 是 “a2>b2”的必要条件;
(3) “a>b” 是 “ac2>bc2”的充分条件;
(4) “a>b” 是 “a+c>b+c”的充要条件;真命题假命题假命题假命题4. 若p 是 的充分不必要条件,则 q 是 的———.充分不必要条件真真假假二判定方法:
(1) 判断时要先认准条件与结论,再判定“若p则q”和“若q则p”的真假,指出充分或必要。
(五)小结一 几个重要概念:
充分而不必要条件充要条件必要而不充分条件既不充分也不必要条件在今后判断p是q的什么条件时主要是指(2)利用互为逆否的命题是等价的命题进行转化:
“ ” “ ”必要条件充分条件充要条件思考题:
关于x的方程ax2+bx+c=0一个根为1的充分且必
要条件是------------。(六)布置作业:
教材 P36 1
P42 11、 12 、13
谢谢!再见
