1.2.2充要条件[上学期]

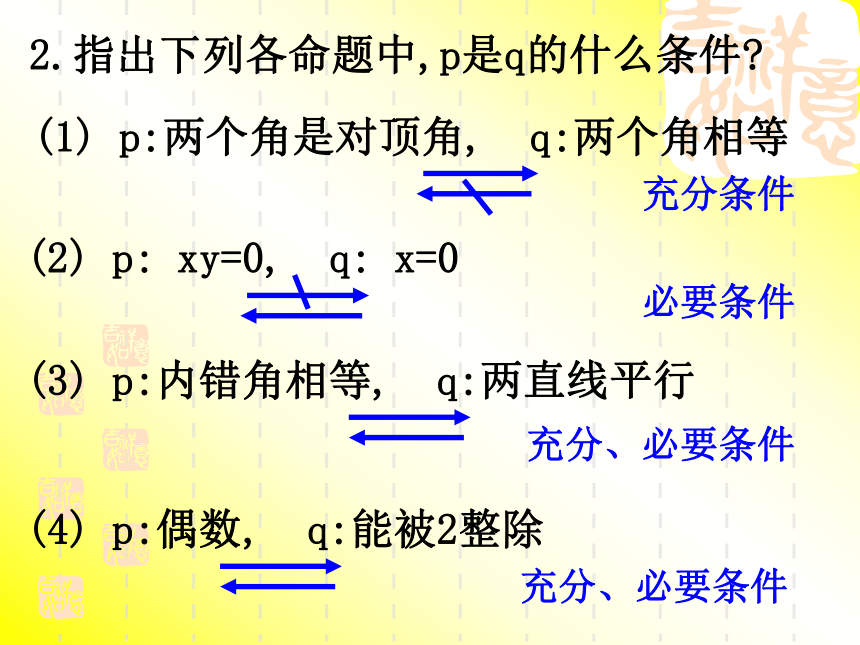
课件13张PPT。1.如何理解: (1) p是q的充分条件复习提问:(2) p是q的必要条件则条件p是结论q成立的充分条件;则条件p是结论成立的必要条件2.指出下列各命题中,p是q的什么条件?(1) p:两个角是对顶角, q:两个角相等充分条件(2) p: xy=0, q: x=0必要条件(3) p:内错角相等, q:两直线平行充分、必要条件(4) p:偶数, q:能被2整除充分、必要条件3.已知p:整数a是6的倍数,q:整数a是2和3的倍数.
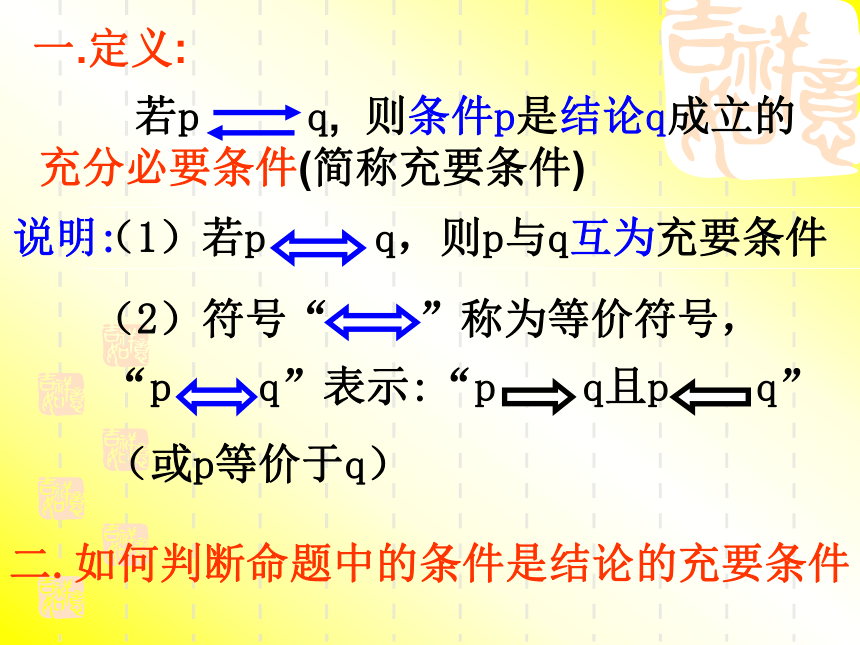
请问:p是q的什么条件? q是p的什么条件?既充分又必要条件1.2.2充要条件一.定义:说明:二.如何判断命题中的条件是结论的充要条件例1 指出下列各组命题中,p是q的什么条件 (在“充分而不必要”、“必要而不充分”、 “充要”、“既不充分也不必要”中选一种)(1)p:(x-2)(x-3)=0; q:x-2=0(2)P :同位角相等; q:两直线平行(3)p:x=3; q:x2=9(4)p:四边形的对角线相等; q:四边形是平行四边形必要不充分充要充分不必要既不充分又不必要(1)p:x是6的倍数; q:x是2的倍数(2)p:x是2的倍数; q:x是6的倍数(3)p:x既是2的倍数也是3的倍数; q:x是6的倍数(4)p:x是4的倍数; q:x是6的倍数充分不必要必要不充分充要既不充分又不必要例2.下列命题中,p是q的什么条件?例3.下列命题中,哪些p是q的充要条件?(1)p:b=0, q:函数f(x)=ax2+bx+c是偶函数(2)p: x>0,y>0, q:xy>0(3)p:a>b, q:a+c>b+c充要条件充分不必要充要条件故选(1)(2)例4.已知:圆O的半径r,圆心O到直线l 的距离为d,求证:d=r是直线l 与圆O相切的充要条件证明：如图，作OP l于点P，则OP＝d．设p:d=r, q:直线l 与圆O相切分析:lQP0┐d 若d=r,则点P在圆O上。在直线l上任取一点Q(异于点P),连接OQ。在RtΔOPQ中, OQ>OP=r。所以,除点P外,直线l 上的点都在圆O的外部。即直线l 与圆O仅有一个公共点P。因此,直线l 与圆O相切。 若直线l 与圆O相切,不妨设切点为P,则OP l.因此,d=OP=r。故d=r是直线l 与圆O相切的充要条件。例５．证明：ax２＋bx＋c＝０有两个实根的充要条件是b２－４ac≥０结论q: ax2+bx+c=0有两个实根条件p: b２－４ac≥０分析：证明：∵b２－４ac≥０设方程ax2+bx+c=0的根为即方程ax2+bx+c=0有两个实根∵方程ax2+bx+c=0有两个实根∴b２－４ac≥０故方程有两个实根的充要条件是b２－４ac≥０小结条件p　　 结论q条件p是结论q成立的充分不必要条件条件p　　　结论q条件p是结论q成立的必要不充分条件条件p　　　结论q条件p是结论q成立的充要条件说明：首先分清命题中的条件p与结论q,然后根据定义判断命题中的条件p是结论q成立的什么条件(充分、必要、充要)作业1. P14练习 1、2
2. P14习题1.2
A组1、2、3、4
B组1、2