9年级数学北师大版下册 1.4解直角三角形 课时练(含答案)
文档属性
| 名称 | 9年级数学北师大版下册 1.4解直角三角形 课时练(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 176.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-28 00:00:00 | ||
图片预览

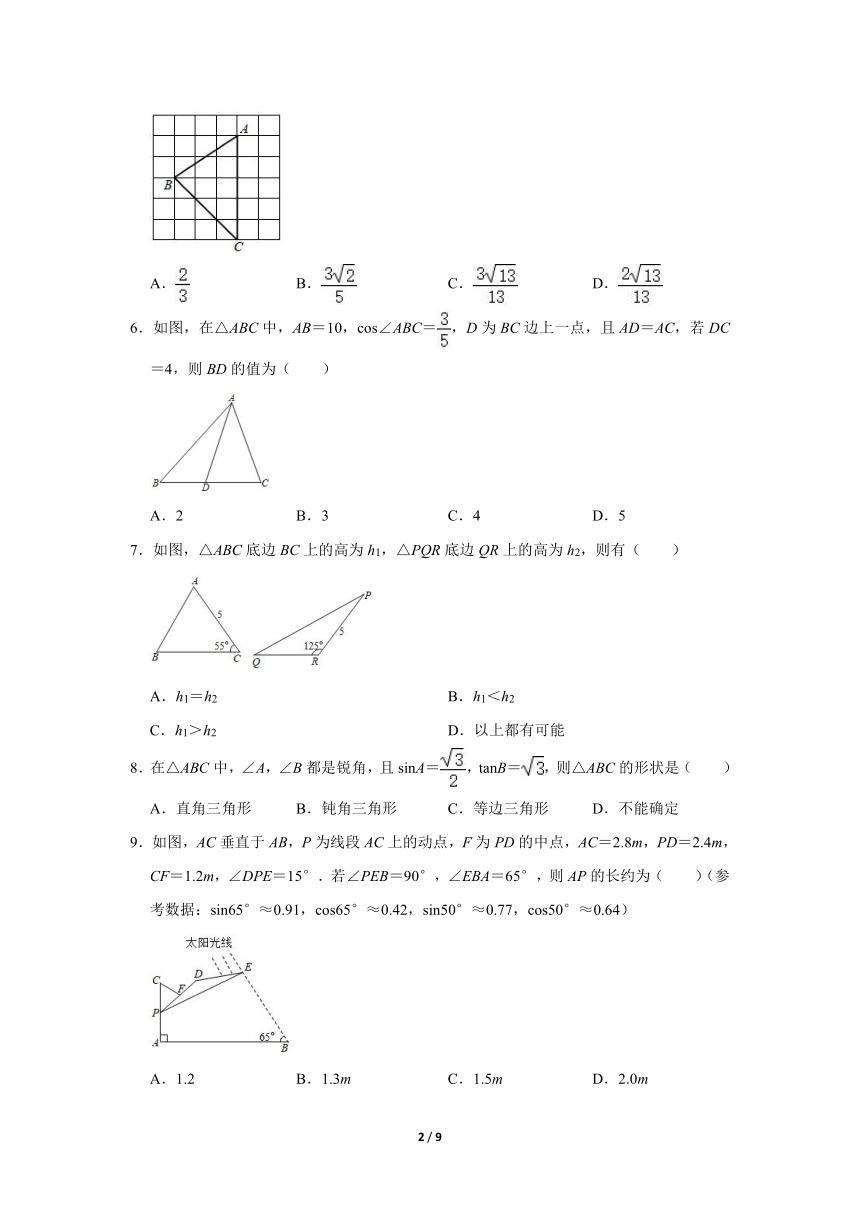


文档简介
课 时 练
第1单元 直角三角形的边角关系
解直角三角形
1.如图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C在格点上,则∠A正切值是( )
A. B. C.2 D.
2.如图,在Rt△ABC中,∠C=90°,AB=4,sinA=,则BC的长为( )
A.2 B.3 C. D.2
3.如图,在3×3的网格中,A,B均为格点,以点A为圆心,AB的长为半径作弧,图中的点C是该弧与格线的交点,则tan∠BAC的值是( )
A. B. C. D.
4.已知△ABC中,AC=4,BC=3,AB=5,则sinB=( )
A. B. C. D.
5.如图,△ABC的顶点在正方形网格的格点上,则sinA的值为( )
A. B. C. D.
6.如图,在△ABC中,AB=10,cos∠ABC=,D为BC边上一点,且AD=AC,若DC=4,则BD的值为( )
A.2 B.3 C.4 D.5
7.如图,△ABC底边BC上的高为h1,△PQR底边QR上的高为h2,则有( )
A.h1=h2 B.h1<h2
C.h1>h2 D.以上都有可能
8.在△ABC中,∠A,∠B都是锐角,且sinA=,tanB=,则△ABC的形状是( )
A.直角三角形 B.钝角三角形 C.等边三角形 D.不能确定
9.如图,AC垂直于AB,P为线段AC上的动点,F为PD的中点,AC=2.8m,PD=2.4m,CF=1.2m,∠DPE=15°.若∠PEB=90°,∠EBA=65°,则AP的长约为( )(参考数据:sin65°≈0.91,cos65°≈0.42,sin50°≈0.77,cos50°≈0.64)
A.1.2 B.1.3m C.1.5m D.2.0m
10.如图,在Rt△ABC中,∠ACB=90°,tan∠BAC=,CD是斜边AB上的中线,点E是直线AC左侧一点,联结AE、CE、ED,若EC⊥CD,∠EAC=∠B,则的值为 .
11.△ABC中,∠B为锐角,cosB=,AB=,AC=2,则∠ACB的度数为 .
12.已知△ABC中,AB=8,∠ABC=60°,AC=7,则△ABC的面积是 .
13.如图,在△ABC中,∠A=90°,斜边BC的垂直平分线分别交AB、BC交于点D、E,如果cosB=,AB=7,那么CD的长等于 .
14.在平面直角坐标系xOy中,已知点A的坐标为(2,3),那么直线OA与x轴夹角的正切值是 .
15.如图,△ABC中,∠ACB=90°,AC=BC,点D、点E分别在AB、AC上,连接CD、ED,ED=CD,tan∠ADE=,BD=,则AB= .
16.如果等腰三角形中的两条边长分别是2和5,那么底角的余弦为 .
17.课堂上小刚进行如下实践操作:第一步,将一张矩形纸片利用图1的方法折出一个正方形,然后把纸片展平;第二步,如图2,把这个正方形折成两个全等的矩形,然后把纸片展平;第三步,如图3,折出内侧矩形AFBC的对角线AB,并把AB沿AQ对折到AD处,则tan∠BAQ= .
三.解答题(共5小题)
18.如图,在△ABC中,BD⊥AC,AB=4,AC=3,∠A=30°.
(1)求AD的长. (2)求sinC的值.
19.如图,已知△ABC中,AB=AC=12,cosB=,AP⊥AB,交BC于点P.
(1)求CP的长;
(2)求∠PAC的正弦值.
20.如图,在Rt△ABC中,∠BAC=90°,AD是BC边上的高,若sin∠CAD=,BC=25,求AC的长.
21.如图,A、B、D三点在同一水平线上,CD⊥AD,∠A=45°,∠CBD=75°,AB=60m.
(1)求∠ACB的度数;
(2)求线段CB的长度.
22.把矩形纸片ABCD,先沿AE折叠使点B落在AD边上的B',再沿AC折叠,恰好点E也落到AD上,记为E'.
求:(1)∠B'EE'的度数;
(2)∠DAC的正切值.
参考答案
1.D
2.A
3.B
4.B
5.C
6.C
7.A
8.C
9.B
10. .
11. 60°或120°.
12. 10或6.
13. .
14. .
15. 3,
16. .
17. .
18.解:(1)在Rt△ABD中,∠ADB=90°,AB=4,∠A=30°,
∴BD=AB=2,AD=BD=2;
(2)∵AC=3,AD=2,
∴CD=AC﹣AD=.
在Rt△CBD中,∠CDB=90°,BD=2,CD=,
∴BC==,
sinC===.
19.解:(1)过点A作AD⊥BC于D,
在Rt△ABD中,AB=12,cosB=,
∴BD=cosB AB=9,
∵AB=AC,
∴BD=CD=9,∠B=∠C,
∵AP⊥AB,
∴∠PAB=90°,
在Rt△ABP中,AB=12,cosB=,
∴BP==16,
∴PC=BC﹣BP
=9×2﹣16
=2;
(2)过点P作PE⊥AC于E,
在Rt△PCE中,PC=2,cosC=cosB=,
∴CE=cosC PC=2×=,
∴PE==,
AP=
=
=
=4,
∴sin∠PAC==.
20.解:∵∠BAC=90°,
∴∠CAD+∠BAD=90°,
∵AD是BC边上的高,
∴∠ADC=∠B+∠BAD=90°,
∴∠B=∠CAD,
∴sinB=sin∠CAD=.
在Rt△ABC中,∠BAC=90°,sinB=,BC=25,
∴AC=BC sinB=25×=15.
21.解:(1)∵∠CBD=∠A+∠ACB,∠A=45°,∠CBD=75°,
∴∠ACB=75°﹣45°=30°.
(2)如图,过点B作BH⊥AC于H.
∵∠BHA=90°,AB=60m,∠A=45°,
∴BH=AB sin45°=60(m),
∵∠BCH=30°,
∴BC=2BH=120(m).
22.解:(1)由折叠性质可知,∠ABE=∠AB'E=90°,AB=AB',
又∠BAB'=90°,
∴四边形ABEB'为矩形,
又AB=AB',
∴四边形ABEB'为正方形.
∴∠B'AE=∠AEB'=45°.
又沿AC折叠,点E也落到AD上,故AE=AE',
∴∠AEE'=∠AE'E==67.5°,
∴∠B'EE'=∠AEE'﹣∠AEB'=67.5°﹣45°=22.5°.
(2)设正方形ABEB'的边长为a,如图所示.
则AB=BE=EB'=B'A=a,AE==AE',
∴B'E'=AE'﹣AB'=,
由折叠可知,AC垂直平分EE',
∴∠DAC+∠AE'F=90°,
又∠B'EE'+∠AE'E=90°,
∴∠DAC=∠B'EE',
∴tan∠DAC=tan∠B'EE'===.
7 / 9
第1单元 直角三角形的边角关系
解直角三角形
1.如图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C在格点上,则∠A正切值是( )
A. B. C.2 D.
2.如图,在Rt△ABC中,∠C=90°,AB=4,sinA=,则BC的长为( )
A.2 B.3 C. D.2
3.如图,在3×3的网格中,A,B均为格点,以点A为圆心,AB的长为半径作弧,图中的点C是该弧与格线的交点,则tan∠BAC的值是( )
A. B. C. D.
4.已知△ABC中,AC=4,BC=3,AB=5,则sinB=( )
A. B. C. D.
5.如图,△ABC的顶点在正方形网格的格点上,则sinA的值为( )
A. B. C. D.
6.如图,在△ABC中,AB=10,cos∠ABC=,D为BC边上一点,且AD=AC,若DC=4,则BD的值为( )
A.2 B.3 C.4 D.5
7.如图,△ABC底边BC上的高为h1,△PQR底边QR上的高为h2,则有( )
A.h1=h2 B.h1<h2
C.h1>h2 D.以上都有可能
8.在△ABC中,∠A,∠B都是锐角,且sinA=,tanB=,则△ABC的形状是( )
A.直角三角形 B.钝角三角形 C.等边三角形 D.不能确定
9.如图,AC垂直于AB,P为线段AC上的动点,F为PD的中点,AC=2.8m,PD=2.4m,CF=1.2m,∠DPE=15°.若∠PEB=90°,∠EBA=65°,则AP的长约为( )(参考数据:sin65°≈0.91,cos65°≈0.42,sin50°≈0.77,cos50°≈0.64)
A.1.2 B.1.3m C.1.5m D.2.0m
10.如图,在Rt△ABC中,∠ACB=90°,tan∠BAC=,CD是斜边AB上的中线,点E是直线AC左侧一点,联结AE、CE、ED,若EC⊥CD,∠EAC=∠B,则的值为 .
11.△ABC中,∠B为锐角,cosB=,AB=,AC=2,则∠ACB的度数为 .
12.已知△ABC中,AB=8,∠ABC=60°,AC=7,则△ABC的面积是 .
13.如图,在△ABC中,∠A=90°,斜边BC的垂直平分线分别交AB、BC交于点D、E,如果cosB=,AB=7,那么CD的长等于 .
14.在平面直角坐标系xOy中,已知点A的坐标为(2,3),那么直线OA与x轴夹角的正切值是 .
15.如图,△ABC中,∠ACB=90°,AC=BC,点D、点E分别在AB、AC上,连接CD、ED,ED=CD,tan∠ADE=,BD=,则AB= .
16.如果等腰三角形中的两条边长分别是2和5,那么底角的余弦为 .
17.课堂上小刚进行如下实践操作:第一步,将一张矩形纸片利用图1的方法折出一个正方形,然后把纸片展平;第二步,如图2,把这个正方形折成两个全等的矩形,然后把纸片展平;第三步,如图3,折出内侧矩形AFBC的对角线AB,并把AB沿AQ对折到AD处,则tan∠BAQ= .
三.解答题(共5小题)
18.如图,在△ABC中,BD⊥AC,AB=4,AC=3,∠A=30°.
(1)求AD的长. (2)求sinC的值.
19.如图,已知△ABC中,AB=AC=12,cosB=,AP⊥AB,交BC于点P.
(1)求CP的长;
(2)求∠PAC的正弦值.
20.如图,在Rt△ABC中,∠BAC=90°,AD是BC边上的高,若sin∠CAD=,BC=25,求AC的长.
21.如图,A、B、D三点在同一水平线上,CD⊥AD,∠A=45°,∠CBD=75°,AB=60m.
(1)求∠ACB的度数;
(2)求线段CB的长度.
22.把矩形纸片ABCD,先沿AE折叠使点B落在AD边上的B',再沿AC折叠,恰好点E也落到AD上,记为E'.
求:(1)∠B'EE'的度数;
(2)∠DAC的正切值.
参考答案
1.D
2.A
3.B
4.B
5.C
6.C
7.A
8.C
9.B
10. .
11. 60°或120°.
12. 10或6.
13. .
14. .
15. 3,
16. .
17. .
18.解:(1)在Rt△ABD中,∠ADB=90°,AB=4,∠A=30°,
∴BD=AB=2,AD=BD=2;
(2)∵AC=3,AD=2,
∴CD=AC﹣AD=.
在Rt△CBD中,∠CDB=90°,BD=2,CD=,
∴BC==,
sinC===.
19.解:(1)过点A作AD⊥BC于D,
在Rt△ABD中,AB=12,cosB=,
∴BD=cosB AB=9,
∵AB=AC,
∴BD=CD=9,∠B=∠C,
∵AP⊥AB,
∴∠PAB=90°,
在Rt△ABP中,AB=12,cosB=,
∴BP==16,
∴PC=BC﹣BP
=9×2﹣16
=2;
(2)过点P作PE⊥AC于E,
在Rt△PCE中,PC=2,cosC=cosB=,
∴CE=cosC PC=2×=,
∴PE==,
AP=
=
=
=4,
∴sin∠PAC==.
20.解:∵∠BAC=90°,
∴∠CAD+∠BAD=90°,
∵AD是BC边上的高,
∴∠ADC=∠B+∠BAD=90°,
∴∠B=∠CAD,
∴sinB=sin∠CAD=.
在Rt△ABC中,∠BAC=90°,sinB=,BC=25,
∴AC=BC sinB=25×=15.
21.解:(1)∵∠CBD=∠A+∠ACB,∠A=45°,∠CBD=75°,
∴∠ACB=75°﹣45°=30°.
(2)如图,过点B作BH⊥AC于H.
∵∠BHA=90°,AB=60m,∠A=45°,
∴BH=AB sin45°=60(m),
∵∠BCH=30°,
∴BC=2BH=120(m).
22.解:(1)由折叠性质可知,∠ABE=∠AB'E=90°,AB=AB',
又∠BAB'=90°,
∴四边形ABEB'为矩形,
又AB=AB',
∴四边形ABEB'为正方形.
∴∠B'AE=∠AEB'=45°.
又沿AC折叠,点E也落到AD上,故AE=AE',
∴∠AEE'=∠AE'E==67.5°,
∴∠B'EE'=∠AEE'﹣∠AEB'=67.5°﹣45°=22.5°.
(2)设正方形ABEB'的边长为a,如图所示.
则AB=BE=EB'=B'A=a,AE==AE',
∴B'E'=AE'﹣AB'=,
由折叠可知,AC垂直平分EE',
∴∠DAC+∠AE'F=90°,
又∠B'EE'+∠AE'E=90°,
∴∠DAC=∠B'EE',
∴tan∠DAC=tan∠B'EE'===.
7 / 9
