北师大版九年级下册1.6《利用三角函数测高》课时练(含答案)
文档属性
| 名称 | 北师大版九年级下册1.6《利用三角函数测高》课时练(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 217.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-29 08:18:13 | ||
图片预览


文档简介
课 时 练
第1单元 直角三角形的边角关系
利用三角函数测高
一、 选择题
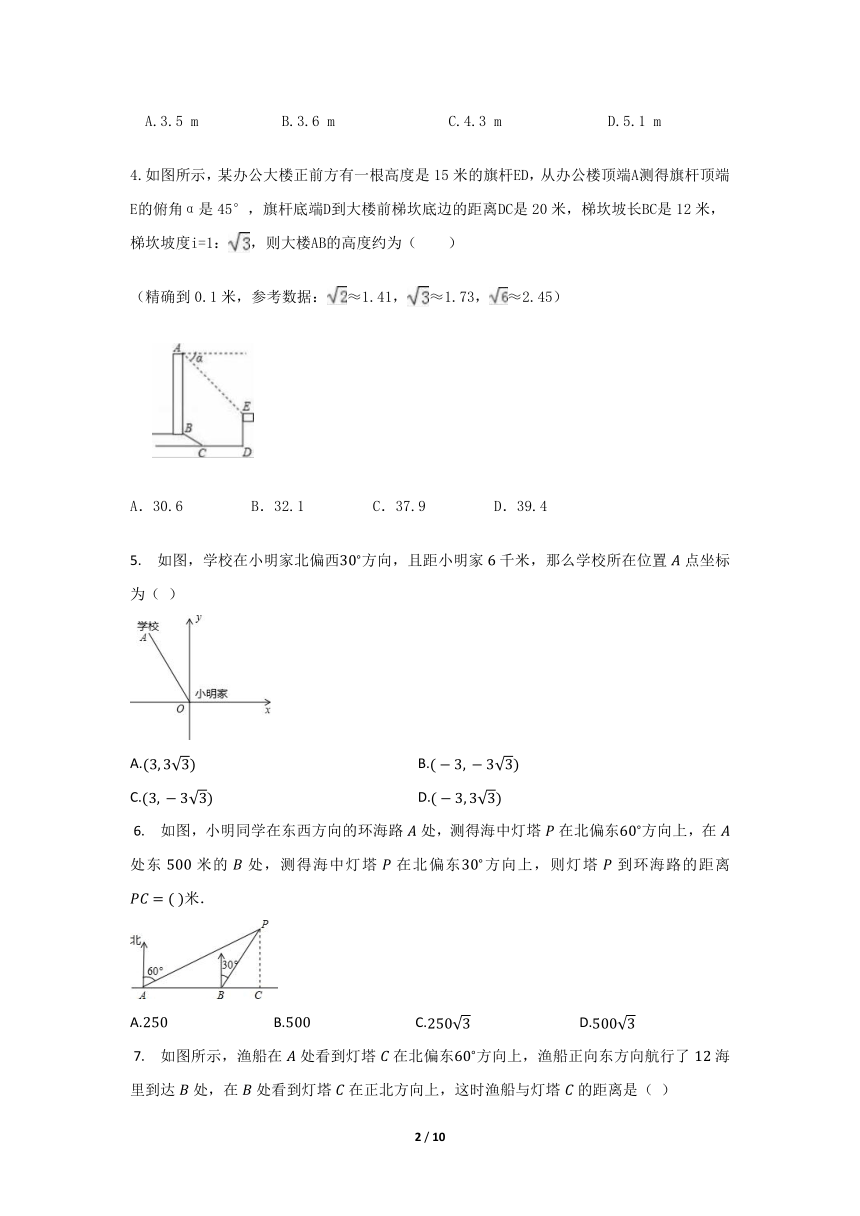
1. 如图,飞机在空中处探测得地面目标处的俯角为,此时飞机高度为,则的长度是( )
A. B. C. D.
2.在湖边高出水面50 m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°.则飞艇离开湖面的高度( )
A. B. C. D.
3.如图,小敏同学想测量一棵大树的高度.她站在B处仰望树顶,测得仰角为30°,再往大树的方向前进4 m,测得仰角为60°,已知小敏同学身高(AB)为1.6 m,则这棵树的高度约为(结果精确到0.1 m,≈1.73)( )
A.3.5 m B.3.6 m C.4.3 m D.5.1 m
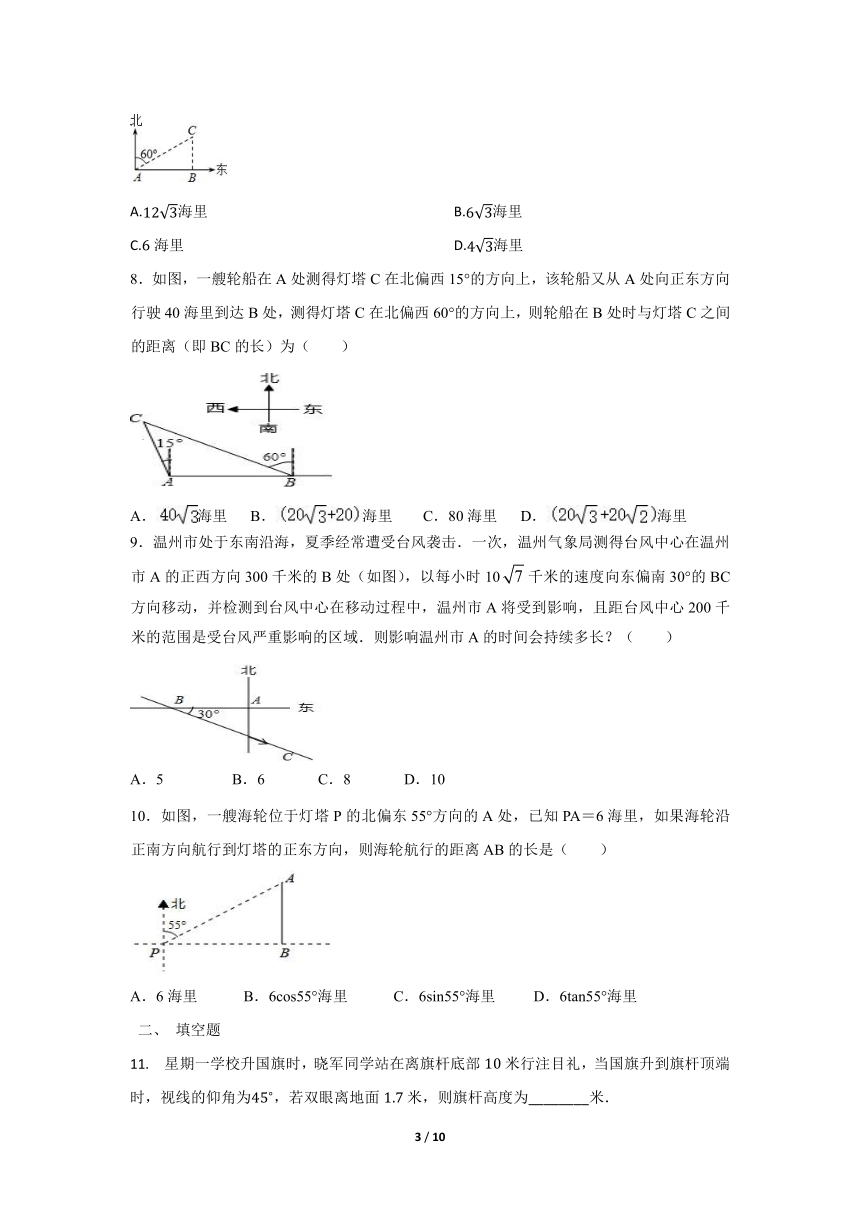
4.如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:,则大楼AB的高度约为( )
(精确到0.1米,参考数据:≈1.41,≈1.73,≈2.45)
A.30.6 B.32.1 C.37.9 D.39.4
5. 如图,学校在小明家北偏西方向,且距小明家千米,那么学校所在位置点坐标为( )
A. B.
C. D.
6. 如图,小明同学在东西方向的环海路处,测得海中灯塔在北偏东方向上,在处东米的处,测得海中灯塔在北偏东方向上,则灯塔到环海路的距离 米.
A. B. C. D.
7. 如图所示,渔船在处看到灯塔在北偏东方向上,渔船正向东方向航行了海里到达处,在处看到灯塔在正北方向上,这时渔船与灯塔的距离是( )
A.海里 B.海里
C.海里 D.海里
8.如图,一艘轮船在A处测得灯塔C在北偏西15°的方向上,该轮船又从A处向正东方向行驶40海里到达B处,测得灯塔C在北偏西60°的方向上,则轮船在B处时与灯塔C之间的距离(即BC的长)为( )
A.海里 B.海里 C.80海里 D.海里
9.温州市处于东南沿海,夏季经常遭受台风袭击.一次,温州气象局测得台风中心在温州市A的正西方向300千米的B处(如图),以每小时10千米的速度向东偏南30°的BC方向移动,并检测到台风中心在移动过程中,温州市A将受到影响,且距台风中心200千米的范围是受台风严重影响的区域.则影响温州市A的时间会持续多长?( )
A.5 B.6 C.8 D.10
10.如图,一艘海轮位于灯塔P的北偏东55°方向的A处,已知PA=6海里,如果海轮沿正南方向航行到灯塔的正东方向,则海轮航行的距离AB的长是( )
A.6海里 B.6cos55°海里 C.6sin55°海里 D.6tan55°海里
二、 填空题
11. 星期一学校升国旗时,晓军同学站在离旗杆底部米行注目礼,当国旗升到旗杆顶端时,视线的仰角为,若双眼离地面米,则旗杆高度为________米.
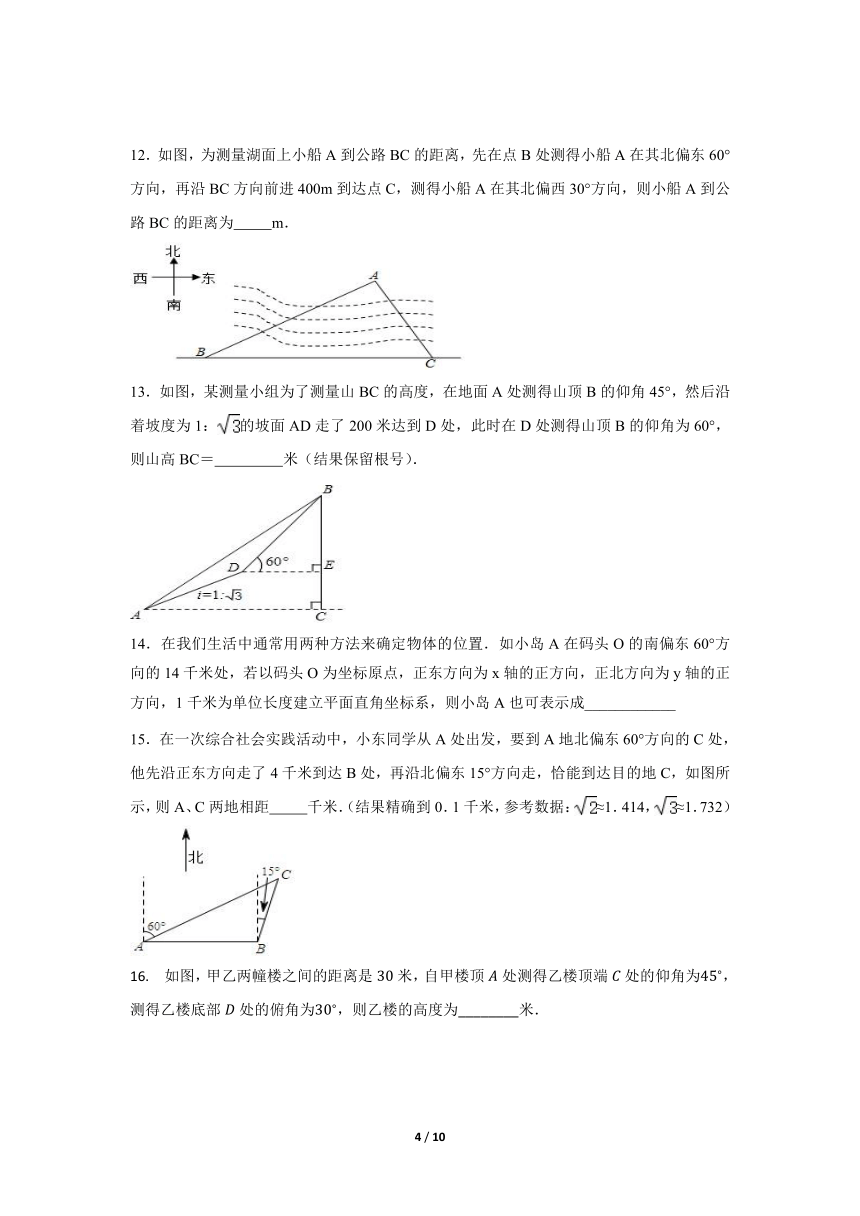
12.如图,为测量湖面上小船A到公路BC的距离,先在点B处测得小船A在其北偏东60°方向,再沿BC方向前进400m到达点C,测得小船A在其北偏西30°方向,则小船A到公路BC的距离为 m.
13.如图,某测量小组为了测量山BC的高度,在地面A处测得山顶B的仰角45°,然后沿着坡度为1:的坡面AD走了200米达到D处,此时在D处测得山顶B的仰角为60°,则山高BC= 米(结果保留根号).
14.在我们生活中通常用两种方法来确定物体的位置.如小岛A在码头O的南偏东60°方向的14千米处,若以码头O为坐标原点,正东方向为x轴的正方向,正北方向为y轴的正方向,1千米为单位长度建立平面直角坐标系,则小岛A也可表示成____________
15.在一次综合社会实践活动中,小东同学从A处出发,要到A地北偏东60°方向的C处,他先沿正东方向走了4千米到达B处,再沿北偏东15°方向走,恰能到达目的地C,如图所示,则A、C两地相距 千米.(结果精确到0.1千米,参考数据:≈1.414,≈1.732)
16. 如图,甲乙两幢楼之间的距离是米,自甲楼顶处测得乙楼顶端处的仰角为,测得乙楼底部处的俯角为,则乙楼的高度为________米.
三、 解答题
17.如图,一枚运载火箭从地面L处发射,当火箭到达A点时,从位于地面R处的雷达站测得AR的距离是6km,仰角为43°;1s后火箭到达B点,此时测得仰角为45.54°(所有结果取小数点后两位).
(1)求地面雷达站R到发射处L的水平距离;
(2)求这枚火箭从A到B的平均速度是多少?
(参考数据:sin43°≈0.68,cos43°≈0.73,tan43°≈0.93,sin45.54°≈0.71,cos45.54°≈0.70,tan45.54°≈1.02)
18.如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值)
19.鄂州市某校数学兴趣小组借助无人机测量一条河流的宽度CD.如图所示,一架水平飞行的无人机在A处测得正前方河流的左岸C处的俯角为α,无人机沿水平线AF方向继续飞行50米至B处,测得正前方河流右岸D处的俯角为30°.线段AM的长为无人机距地面的铅直高度,点M、C、D在同一条直线上.其中tanα=2,MC=50米.
(1)求无人机的飞行高度AM;(结果保留根号)
(2)求河流的宽度CD.(结果精确到1米,参考数据:≈1.41,≈1.73)
20 数学爱好小组要测量信号基站高度,一名同学站在距离信号基站的点处,测得基站顶部的仰角,已知测角仪的高度.求这个信号基站的高(精确到).(参考数据: ,,)
21 某中学九年级数学兴趣小组想测量建筑物的高度.他们在处仰望建筑物顶端,测得仰角为,再往建筑物的方向前进米到达处,测得仰角为,求建筑物的高度.(测角器的高度忽略不计,结果精确到米)
(参考数据:,,,)
22 如图,广场上有一个充满氢气的气球,被广告条拽着悬在空中,甲、乙二人分别从,处看气球的仰角分别是、,点与点的高度差为米,水平距离为米,的高度为米,请问此气球离地面的高度是多少?结果保留到米,参考数据:
参考答案
1.B.
2.D.
3.D
4.D
5. D
6. C
7. D
8.B
9.D
10.B
11.
12.100.
13.(100+100).
14.(7,-7).
15.5.5.
16.
17.解:(1)在Rt△ARL中,RL=AR cos43°≈4.38(km)
(2)在Rt△ARL中,AL=AR sin43°≈4.08
在Rt△BRL中,BL=RL tan45.54°≈4.468
∴AB=BL﹣AL=0.388≈0.39(km)
∴速度为0.39km/s
答:雷达站到发射处的水平距离为4.38km,这枚火箭从A到B的平均速度为0.39km/s.
18.解: 如图,过B作AB的垂线,过C作AB的平行线,两线交于点E;过C作AB的垂线,过D作AB的平行线,两线交于点F,则∠E=∠F=90°,拦截点D处到公路的距离DA=BE+CF.
在Rt△BCE中,∵∠E=90°,∠CBE=60°,
∴∠BCE=30°,
∴BE=BC=×1000=500米;
在Rt△CDF中,∵∠F=90°,∠DCF=45°,CD=AB=1000米,
∴CF=CD=500米,
∴DA=BE+CF=(500+500)米,
故拦截点D处到公路的距离是(500+500)米.
19.解:过点B作BN⊥MD,垂足为N,由题意可知,
∠ACM=α,∠BDM=30°,AB=MN=50,
(1)在Rt△ACM中,tan∠ACM=tanα=2,MC=50,
∴AM=2MC=100=BN,
答:无人机的飞行高度AM为100米;
(2)在Rt△BND中,
∵tan∠BDN=,即:tan30°=,
∴DN=300,
∴DM=DN+MN=300+50=350,
∴CD=DM﹣MC=350﹣50≈263,
答:河流的宽度CD约为263米.
20.这个信号基站的高度为.
21.建筑物的高度约为米.
22.【答案】
解:设米
∵ ,
∴ ,
∴ ,
在中,
∵ ,
∴ ,,
∴ 米,
∴ 米.
【解答】
解:设米
∵ ,
∴ ,
∴ ,
在中,
∵ ,
∴ ,,
∴ 米,
∴ 米.
10 / 10
第1单元 直角三角形的边角关系
利用三角函数测高
一、 选择题
1. 如图,飞机在空中处探测得地面目标处的俯角为,此时飞机高度为,则的长度是( )
A. B. C. D.
2.在湖边高出水面50 m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°.则飞艇离开湖面的高度( )
A. B. C. D.
3.如图,小敏同学想测量一棵大树的高度.她站在B处仰望树顶,测得仰角为30°,再往大树的方向前进4 m,测得仰角为60°,已知小敏同学身高(AB)为1.6 m,则这棵树的高度约为(结果精确到0.1 m,≈1.73)( )
A.3.5 m B.3.6 m C.4.3 m D.5.1 m
4.如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:,则大楼AB的高度约为( )
(精确到0.1米,参考数据:≈1.41,≈1.73,≈2.45)
A.30.6 B.32.1 C.37.9 D.39.4
5. 如图,学校在小明家北偏西方向,且距小明家千米,那么学校所在位置点坐标为( )
A. B.
C. D.
6. 如图,小明同学在东西方向的环海路处,测得海中灯塔在北偏东方向上,在处东米的处,测得海中灯塔在北偏东方向上,则灯塔到环海路的距离 米.
A. B. C. D.
7. 如图所示,渔船在处看到灯塔在北偏东方向上,渔船正向东方向航行了海里到达处,在处看到灯塔在正北方向上,这时渔船与灯塔的距离是( )
A.海里 B.海里
C.海里 D.海里
8.如图,一艘轮船在A处测得灯塔C在北偏西15°的方向上,该轮船又从A处向正东方向行驶40海里到达B处,测得灯塔C在北偏西60°的方向上,则轮船在B处时与灯塔C之间的距离(即BC的长)为( )
A.海里 B.海里 C.80海里 D.海里
9.温州市处于东南沿海,夏季经常遭受台风袭击.一次,温州气象局测得台风中心在温州市A的正西方向300千米的B处(如图),以每小时10千米的速度向东偏南30°的BC方向移动,并检测到台风中心在移动过程中,温州市A将受到影响,且距台风中心200千米的范围是受台风严重影响的区域.则影响温州市A的时间会持续多长?( )
A.5 B.6 C.8 D.10
10.如图,一艘海轮位于灯塔P的北偏东55°方向的A处,已知PA=6海里,如果海轮沿正南方向航行到灯塔的正东方向,则海轮航行的距离AB的长是( )
A.6海里 B.6cos55°海里 C.6sin55°海里 D.6tan55°海里
二、 填空题
11. 星期一学校升国旗时,晓军同学站在离旗杆底部米行注目礼,当国旗升到旗杆顶端时,视线的仰角为,若双眼离地面米,则旗杆高度为________米.
12.如图,为测量湖面上小船A到公路BC的距离,先在点B处测得小船A在其北偏东60°方向,再沿BC方向前进400m到达点C,测得小船A在其北偏西30°方向,则小船A到公路BC的距离为 m.
13.如图,某测量小组为了测量山BC的高度,在地面A处测得山顶B的仰角45°,然后沿着坡度为1:的坡面AD走了200米达到D处,此时在D处测得山顶B的仰角为60°,则山高BC= 米(结果保留根号).
14.在我们生活中通常用两种方法来确定物体的位置.如小岛A在码头O的南偏东60°方向的14千米处,若以码头O为坐标原点,正东方向为x轴的正方向,正北方向为y轴的正方向,1千米为单位长度建立平面直角坐标系,则小岛A也可表示成____________
15.在一次综合社会实践活动中,小东同学从A处出发,要到A地北偏东60°方向的C处,他先沿正东方向走了4千米到达B处,再沿北偏东15°方向走,恰能到达目的地C,如图所示,则A、C两地相距 千米.(结果精确到0.1千米,参考数据:≈1.414,≈1.732)
16. 如图,甲乙两幢楼之间的距离是米,自甲楼顶处测得乙楼顶端处的仰角为,测得乙楼底部处的俯角为,则乙楼的高度为________米.
三、 解答题
17.如图,一枚运载火箭从地面L处发射,当火箭到达A点时,从位于地面R处的雷达站测得AR的距离是6km,仰角为43°;1s后火箭到达B点,此时测得仰角为45.54°(所有结果取小数点后两位).
(1)求地面雷达站R到发射处L的水平距离;
(2)求这枚火箭从A到B的平均速度是多少?
(参考数据:sin43°≈0.68,cos43°≈0.73,tan43°≈0.93,sin45.54°≈0.71,cos45.54°≈0.70,tan45.54°≈1.02)
18.如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值)
19.鄂州市某校数学兴趣小组借助无人机测量一条河流的宽度CD.如图所示,一架水平飞行的无人机在A处测得正前方河流的左岸C处的俯角为α,无人机沿水平线AF方向继续飞行50米至B处,测得正前方河流右岸D处的俯角为30°.线段AM的长为无人机距地面的铅直高度,点M、C、D在同一条直线上.其中tanα=2,MC=50米.
(1)求无人机的飞行高度AM;(结果保留根号)
(2)求河流的宽度CD.(结果精确到1米,参考数据:≈1.41,≈1.73)
20 数学爱好小组要测量信号基站高度,一名同学站在距离信号基站的点处,测得基站顶部的仰角,已知测角仪的高度.求这个信号基站的高(精确到).(参考数据: ,,)
21 某中学九年级数学兴趣小组想测量建筑物的高度.他们在处仰望建筑物顶端,测得仰角为,再往建筑物的方向前进米到达处,测得仰角为,求建筑物的高度.(测角器的高度忽略不计,结果精确到米)
(参考数据:,,,)
22 如图,广场上有一个充满氢气的气球,被广告条拽着悬在空中,甲、乙二人分别从,处看气球的仰角分别是、,点与点的高度差为米,水平距离为米,的高度为米,请问此气球离地面的高度是多少?结果保留到米,参考数据:
参考答案
1.B.
2.D.
3.D
4.D
5. D
6. C
7. D
8.B
9.D
10.B
11.
12.100.
13.(100+100).
14.(7,-7).
15.5.5.
16.
17.解:(1)在Rt△ARL中,RL=AR cos43°≈4.38(km)
(2)在Rt△ARL中,AL=AR sin43°≈4.08
在Rt△BRL中,BL=RL tan45.54°≈4.468
∴AB=BL﹣AL=0.388≈0.39(km)
∴速度为0.39km/s
答:雷达站到发射处的水平距离为4.38km,这枚火箭从A到B的平均速度为0.39km/s.
18.解: 如图,过B作AB的垂线,过C作AB的平行线,两线交于点E;过C作AB的垂线,过D作AB的平行线,两线交于点F,则∠E=∠F=90°,拦截点D处到公路的距离DA=BE+CF.
在Rt△BCE中,∵∠E=90°,∠CBE=60°,
∴∠BCE=30°,
∴BE=BC=×1000=500米;
在Rt△CDF中,∵∠F=90°,∠DCF=45°,CD=AB=1000米,
∴CF=CD=500米,
∴DA=BE+CF=(500+500)米,
故拦截点D处到公路的距离是(500+500)米.
19.解:过点B作BN⊥MD,垂足为N,由题意可知,
∠ACM=α,∠BDM=30°,AB=MN=50,
(1)在Rt△ACM中,tan∠ACM=tanα=2,MC=50,
∴AM=2MC=100=BN,
答:无人机的飞行高度AM为100米;
(2)在Rt△BND中,
∵tan∠BDN=,即:tan30°=,
∴DN=300,
∴DM=DN+MN=300+50=350,
∴CD=DM﹣MC=350﹣50≈263,
答:河流的宽度CD约为263米.
20.这个信号基站的高度为.
21.建筑物的高度约为米.
22.【答案】
解:设米
∵ ,
∴ ,
∴ ,
在中,
∵ ,
∴ ,,
∴ 米,
∴ 米.
【解答】
解:设米
∵ ,
∴ ,
∴ ,
在中,
∵ ,
∴ ,,
∴ 米,
∴ 米.
10 / 10
