北师大版九年级数学下册 3.2 圆的对称性 课时练(含答案)
文档属性
| 名称 | 北师大版九年级数学下册 3.2 圆的对称性 课时练(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 216.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-29 09:27:10 | ||
图片预览


文档简介
课 时 练
第3单元 圆
2 圆的对称性
一、基础训练
1. 下列语句中,不正确的是 ( )
A.圆既是中心对称图形,又是轴对称图形
B.过圆心的直线都是圆的对称轴
C.当圆绕它的圆心旋转89°57'时,不会与原来的圆重合
D.圆的对称轴有无数条,对称中心只有一个
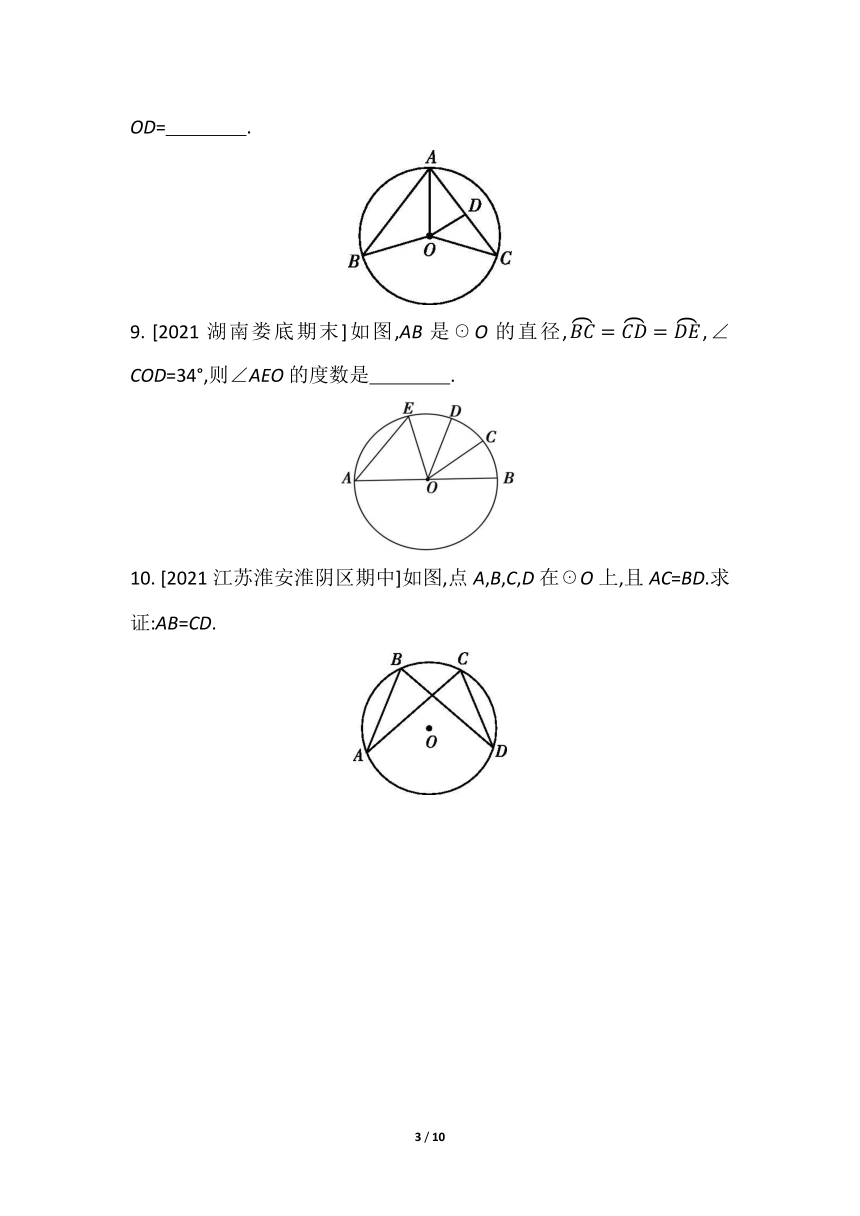
2. 下列图形中表示的角是圆心角的是 ( )
3. [2021甘肃平凉崆峒区期末]在半径为1的☉O中,若弦AB的长为1,则弦AB所对的圆心角的度数为 ( )
A.90° B.60° C.30° D.15°
4. 下列命题是真命题的是 ( )
A.相等的弦所对的弧相等
B.圆心角相等,其所对的弦相等
C.在同圆或等圆中,圆心角不相等,所对的弦不相等
D.弦相等,它所对的圆心角相等
5. [2021江苏泰州月考]如图,AB,CD是☉O的直径,,若∠AOE=32°,则∠COE的度数是 ( )
A.32° B.60° C.68° D.64°
6. [教材P104T4变式]如图,C是☉O上的点,CD⊥OA于点D,CE⊥OB于点E,CD=CE,则与的关系是( )
A. B.
C. D.不能确定
7. 学校有一个圆形花坛,现要求将它三等分,以便在上面种植三种不同的花,你认为下列符合设计要求的图案是 .(将所有符合设计要求的图案序号填上)
8. 如图,在半径为5的☉O中,∠AOB=∠AOC,OD⊥AC于点D,AB=8,则OD= .
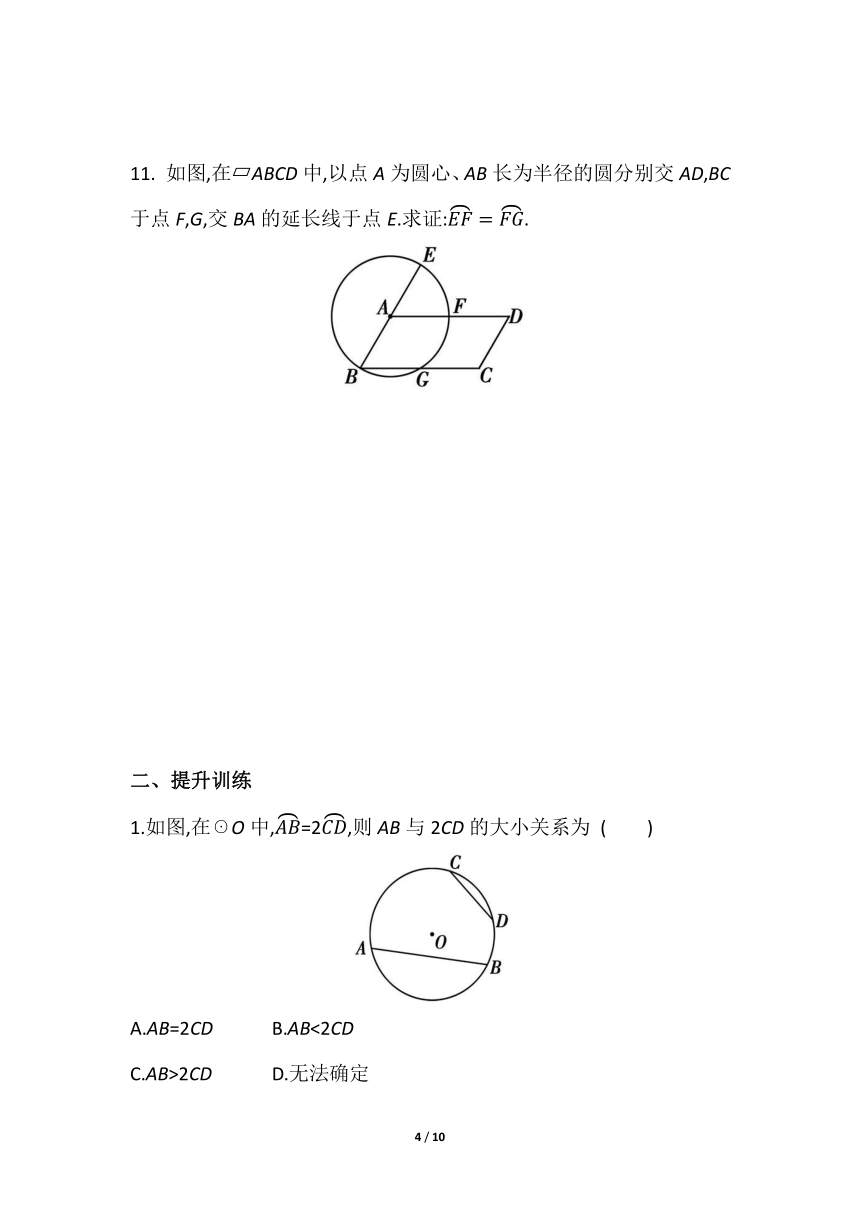
9. [2021湖南娄底期末]如图,AB是☉O的直径,,∠COD=34°,则∠AEO的度数是 .
10. [2021江苏淮安淮阴区期中]如图,点A,B,C,D在☉O上,且AC=BD.求证:AB=CD.
11. 如图,在 ABCD中,以点A为圆心、AB长为半径的圆分别交AD,BC于点F,G,交BA的延长线于点E.求证:.
二、提升训练
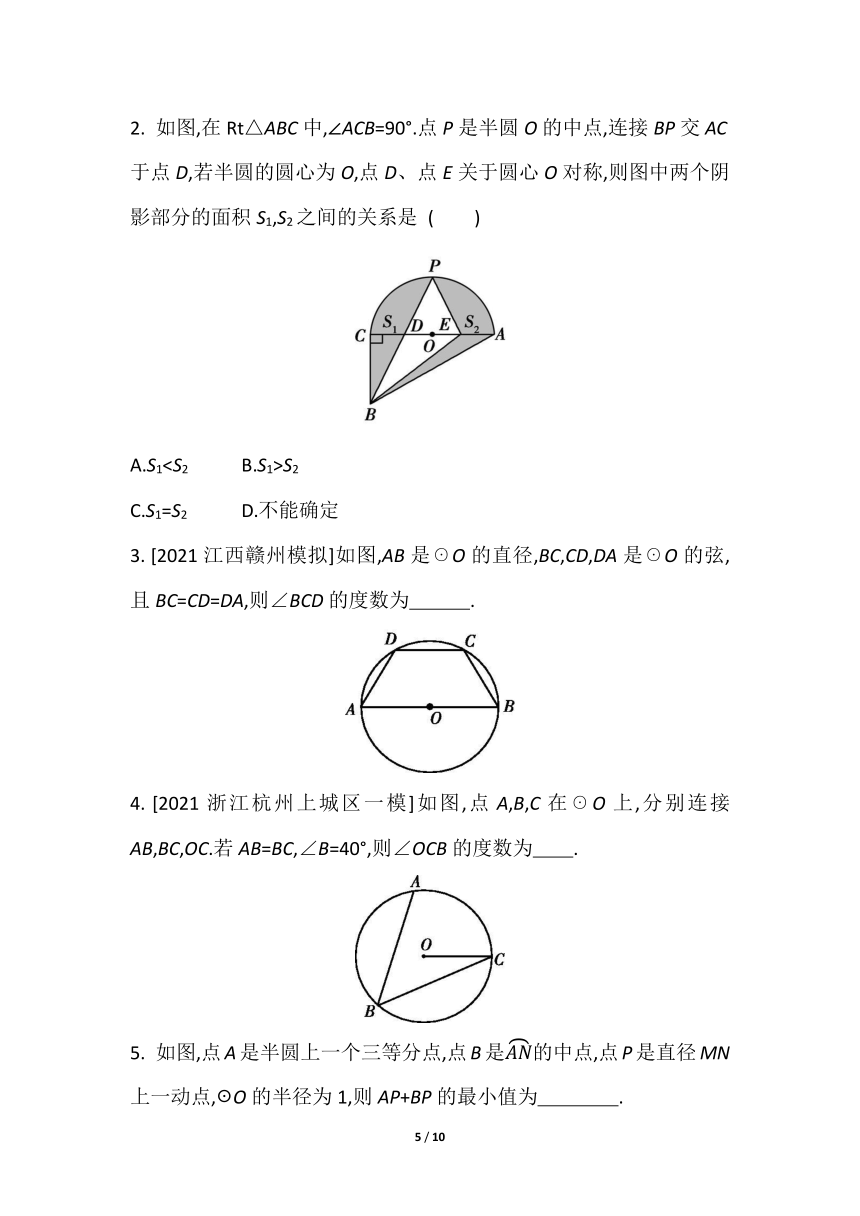
1.如图,在☉O中,=2,则AB与2CD的大小关系为 ( )
A.AB=2CD B.AB<2CD
C.AB>2CD D.无法确定
2. 如图,在Rt△ABC中,∠ACB=90°.点P是半圆O的中点,连接BP交AC于点D,若半圆的圆心为O,点D、点E关于圆心O对称,则图中两个阴影部分的面积S1,S2之间的关系是 ( )
A.S1S2
C.S1=S2 D.不能确定
3. [2021江西赣州模拟]如图,AB是☉O的直径,BC,CD,DA是☉O的弦,且BC=CD=DA,则∠BCD的度数为 .
4. [2021浙江杭州上城区一模]如图,点A,B,C在☉O上,分别连接AB,BC,OC.若AB=BC,∠B=40°,则∠OCB的度数为 .
5. 如图,点A是半圆上一个三等分点,点B是的中点,点P是直径MN上一动点,☉O的半径为1,则AP+BP的最小值为 .
6. [2021江苏宿迁期中]如图,正方形ABCD的四个顶点都在☉O上,M为的中点,连接AM,BM.求证:AM=BM.
7. 如图,在△ABO中,∠A=∠B,☉O与OA交于点C,与OB交于点D,与AB交于点E,F.
求证:.
8. 如图,在☉O中,C,D是直径AB上的两点,且AC=BD,MC⊥AB,ND⊥AB,点M,N在☉O上.
(1)求证:.
(2)若点C,D分别为OA,OB的中点,则成立吗 请说明理由.
参考答案
一、基础训练
1.C
2.A
3.B
4.C
5.D
6.A
7.②③④
8.3
9.51°
10.【解析】 ∵AC=BD,∴,
∴,即,
∴AB=CD.
11.【解析】 如图,连接AG.
∵AD∥BC,∴∠3=∠B,∠1=∠2.
∵AB=AG,∴∠B=∠2,
∴∠3=∠1,∴.
二、提升训练
1.B
2.C
3.120°
4.20°
5.
6.【解析】 ∵四边形ABCD是正方形,
∴AD=BC,∴.
∵M为的中点,∴,
∴,即,∴AM=BM.
7.【解析】 连接OE,OF,则OE=OF,∴∠OEF=∠OFE.
∵∠A=∠B,∠AOE=∠OEF-∠A,∠BOF=∠OFE-∠B,
∴∠AOE=∠BOF,∴.
8.【解析】 (1)如图1,连接OM,ON.
∵OA=OB,AC=BD,
∴OA-AC=OB-BD,即OC=OD.
∵MC⊥AB,ND⊥AB,
∴∠OCM=∠ODN=90°,
又∵OM=ON,∴Rt△OCM≌Rt△ODN,
∴∠AOM=∠BON,∴.
(2)成立.理由如下:
如图2,连接OM,ON,AM,BN.
∵C为OA的中点,
∴AC=OC=AO=MO,
在Rt△MCO中,cos∠AOM=,
∴∠AOM=60°.
同理可得∠BON=60°,
∴∠MON=180°-∠AOM-∠BON=60°,
∴∠AOM=∠MON=∠BON=60°,
∴.
10 / 10
第3单元 圆
2 圆的对称性
一、基础训练
1. 下列语句中,不正确的是 ( )
A.圆既是中心对称图形,又是轴对称图形
B.过圆心的直线都是圆的对称轴
C.当圆绕它的圆心旋转89°57'时,不会与原来的圆重合
D.圆的对称轴有无数条,对称中心只有一个
2. 下列图形中表示的角是圆心角的是 ( )
3. [2021甘肃平凉崆峒区期末]在半径为1的☉O中,若弦AB的长为1,则弦AB所对的圆心角的度数为 ( )
A.90° B.60° C.30° D.15°
4. 下列命题是真命题的是 ( )
A.相等的弦所对的弧相等
B.圆心角相等,其所对的弦相等
C.在同圆或等圆中,圆心角不相等,所对的弦不相等
D.弦相等,它所对的圆心角相等
5. [2021江苏泰州月考]如图,AB,CD是☉O的直径,,若∠AOE=32°,则∠COE的度数是 ( )
A.32° B.60° C.68° D.64°
6. [教材P104T4变式]如图,C是☉O上的点,CD⊥OA于点D,CE⊥OB于点E,CD=CE,则与的关系是( )
A. B.
C. D.不能确定
7. 学校有一个圆形花坛,现要求将它三等分,以便在上面种植三种不同的花,你认为下列符合设计要求的图案是 .(将所有符合设计要求的图案序号填上)
8. 如图,在半径为5的☉O中,∠AOB=∠AOC,OD⊥AC于点D,AB=8,则OD= .
9. [2021湖南娄底期末]如图,AB是☉O的直径,,∠COD=34°,则∠AEO的度数是 .
10. [2021江苏淮安淮阴区期中]如图,点A,B,C,D在☉O上,且AC=BD.求证:AB=CD.
11. 如图,在 ABCD中,以点A为圆心、AB长为半径的圆分别交AD,BC于点F,G,交BA的延长线于点E.求证:.
二、提升训练
1.如图,在☉O中,=2,则AB与2CD的大小关系为 ( )
A.AB=2CD B.AB<2CD
C.AB>2CD D.无法确定
2. 如图,在Rt△ABC中,∠ACB=90°.点P是半圆O的中点,连接BP交AC于点D,若半圆的圆心为O,点D、点E关于圆心O对称,则图中两个阴影部分的面积S1,S2之间的关系是 ( )
A.S1
C.S1=S2 D.不能确定
3. [2021江西赣州模拟]如图,AB是☉O的直径,BC,CD,DA是☉O的弦,且BC=CD=DA,则∠BCD的度数为 .
4. [2021浙江杭州上城区一模]如图,点A,B,C在☉O上,分别连接AB,BC,OC.若AB=BC,∠B=40°,则∠OCB的度数为 .
5. 如图,点A是半圆上一个三等分点,点B是的中点,点P是直径MN上一动点,☉O的半径为1,则AP+BP的最小值为 .
6. [2021江苏宿迁期中]如图,正方形ABCD的四个顶点都在☉O上,M为的中点,连接AM,BM.求证:AM=BM.
7. 如图,在△ABO中,∠A=∠B,☉O与OA交于点C,与OB交于点D,与AB交于点E,F.
求证:.
8. 如图,在☉O中,C,D是直径AB上的两点,且AC=BD,MC⊥AB,ND⊥AB,点M,N在☉O上.
(1)求证:.
(2)若点C,D分别为OA,OB的中点,则成立吗 请说明理由.
参考答案
一、基础训练
1.C
2.A
3.B
4.C
5.D
6.A
7.②③④
8.3
9.51°
10.【解析】 ∵AC=BD,∴,
∴,即,
∴AB=CD.
11.【解析】 如图,连接AG.
∵AD∥BC,∴∠3=∠B,∠1=∠2.
∵AB=AG,∴∠B=∠2,
∴∠3=∠1,∴.
二、提升训练
1.B
2.C
3.120°
4.20°
5.
6.【解析】 ∵四边形ABCD是正方形,
∴AD=BC,∴.
∵M为的中点,∴,
∴,即,∴AM=BM.
7.【解析】 连接OE,OF,则OE=OF,∴∠OEF=∠OFE.
∵∠A=∠B,∠AOE=∠OEF-∠A,∠BOF=∠OFE-∠B,
∴∠AOE=∠BOF,∴.
8.【解析】 (1)如图1,连接OM,ON.
∵OA=OB,AC=BD,
∴OA-AC=OB-BD,即OC=OD.
∵MC⊥AB,ND⊥AB,
∴∠OCM=∠ODN=90°,
又∵OM=ON,∴Rt△OCM≌Rt△ODN,
∴∠AOM=∠BON,∴.
(2)成立.理由如下:
如图2,连接OM,ON,AM,BN.
∵C为OA的中点,
∴AC=OC=AO=MO,
在Rt△MCO中,cos∠AOM=,
∴∠AOM=60°.
同理可得∠BON=60°,
∴∠MON=180°-∠AOM-∠BON=60°,
∴∠AOM=∠MON=∠BON=60°,
∴.
10 / 10
