苏教版(2019)高中数学选择性必修第一册 2.3 圆与圆的位置关系【同步精讲】(解析版)
文档属性
| 名称 | 苏教版(2019)高中数学选择性必修第一册 2.3 圆与圆的位置关系【同步精讲】(解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-29 00:00:00 | ||
图片预览




文档简介
第1章 直线与方程
第01讲 直线的斜率与倾斜角
课程标准 重难点
1.能根据给定圆的方程,判断圆与圆的位置关系.2.能用直线和圆的方程解决一些简单的问题,体会用代数方法处理几何问题的思想. 1.根据圆与圆的位置关系确定两者之间的公切线个数2.公共弦方程
知识点一 圆与圆的位置关系
1.圆与圆的位置关系
圆与圆的位置关系有五种,分别为相离、外切、相交、内切、内含.
2.圆与圆位置关系的判定
(1)几何法:若两圆的半径分别为r1、r2,两圆连心线的长为d,则两圆的位置关系的判断方法如下:
位置关系 外离 外切 相交 内切 内含
图示
d与r1、r2的关系 d>r1+r2 d=r1+r2 |r1-r2|<d<r1+r2 d=|r1-r2| d<|r1-r2|
(2)代数法:设两圆的一般方程为
C1:x2+y2+D1x+E1y+F1=0(D+E-4F1>0),
C2:x2+y2+D2x+E2y+F2=0(D+E-4F2>0),
联立方程得
则方程组解的个数与两圆的位置关系如下:
方程组解的个数 2组 1组 0组
两圆的公共点个数 2个 1个 0个
两圆的位置关系 相交 内切或外切 外离或内含
3.【概念解读】
几何法是利用两圆半径的和或差与圆心距作比较得到两圆的位置关系,代数法则是把两圆位置关系的判定完全转化为代数问题,即方程组的解的个数问题,但这种代数判定方法只能判断出不相交、相交、相切三种位置关系,而不能像几何判定方法一样,能判定出外离、外切、相交、内切、内含五种位置关系,因此一般情况下,使用几何法判定两圆的位置关系问题.
考法01 圆与圆的位置关系
设直线过原点,其倾斜角为,将直线绕坐标原点沿逆时针方向旋转45°,得到直线,则直线1的倾斜角为
【跟踪训练】
1.如果圆C:x2+y2-2ax-2ay+2a2-4=0与圆O:x2+y2=4总相交,那么实数a的取值范围是_________________.
【答案】(-2,0)∪(0,2)
【解析】圆C的标准方程为(x-a)2+(y-a)2=4,
圆心坐标为(a,a),半径为2.
依题意得0<<4,
∴0<|a|<2.∴a∈(-2,0)∪(0,2).
2.已知两圆x2+y2-2x-6y-1=0,x2+y2-10x-12y+m=0.
(1)m取何值时两圆外切?
(2)m取何值时两圆内切?
(3)当m=45时,求两圆的公共弦所在直线的方程和公共弦的长.
【方法总结】
(1)判断两圆的位置关系时常用几何法,即利用两圆圆心之间的距离与两圆半径之间的关系,一般不采用代数法.
(2)若两圆相交,则两圆公共弦所在直线的方程可由两圆的方程作差消去x2,y2项得到.
题组A 基础过关练
1.若圆与圆相交于A,B两点,且两圆在点A处的切线互相垂直,则线段的长是( )
A. B. C.4 D.
2.圆和圆的公共弦的垂直平分线的方程是( )
A. B.
C. D.
3.圆和圆的位置关系为( )
A.内切 B.相交
C.外切 D.外离
4.已知圆,圆,则两圆的公切线的条数是( )
A.1条 B.2条 C.3条 D.4条
5.直线被圆截得的弦长为,则实数______;圆与圆的公共弦所在直线方程是______.
6.两圆与的公切线有___________条.
7.在平面直角坐标系中,若圆和圆关于直线对称,则直线的方程为________.
8.若圆x2+y2=r2与圆x2+y2+2x-4y+4=0有公共点,则r满足的条件是________.
题组B 能力提升练
1.已知圆,,则这两圆的公共弦长为( )
A.2 B. C.2 D.1
2.过点作直线与圆相切于、两点,则直线的方程为( )
A. B. C. D.
3.已知两圆相交于两点,,两圆圆心都在直线上,则的值为( )
A. B. C. D.
4.已知圆与圆的公共弦所在直线恒过点,且点在直线上,则的取值范围是( )
A. B. C. D.
5.圆和圆只有一条公切线,若,,且,则的最小值为___________.
6.已知半径为5的动圆的圆心在直线:上.存在正实数___________,使得动圆中满足与圆:相外切的圆有且仅有一个.
7.已知圆C1:(x-a)2+(y+2)2=4与圆C2:(x+b)2+(y+2)2=1外切,则ab的最大值为_____________.
8.(1)直线经过两直线和的交点,且直线与直线垂直,求直线的方程;
(2)已知以为圆心的圆与圆O:相切,求圆的方程.
题组C 培优拔尖练
1.过圆内一点作直线交圆O于A,B两点,过A,B分别作圆的切线交于点P,则点P的坐标满足方程( )
A. B. C. D.
2.古希腊数学家阿波罗尼奥斯(约公元首262~公元前190年)的著作《圆锥曲线论》是古代世界光辉的科学成果,著作中有这样一个命题:平面内与两定点距离的比为常数k(且)的点的轨迹是圆,后人将这个圆称为阿波罗尼期圆.已知 ,,圆上有且仅有一个点 P满足,则r的取值可以为( )
A.1 B.2 C.3 D.4
3.在平面直角坐标系中,已知点,圆,在圆上存在点满足,则实数的取值范围是
A. B. C. D.
4.已知圆,点,若上存在两点满足,则实数的取值范围___________
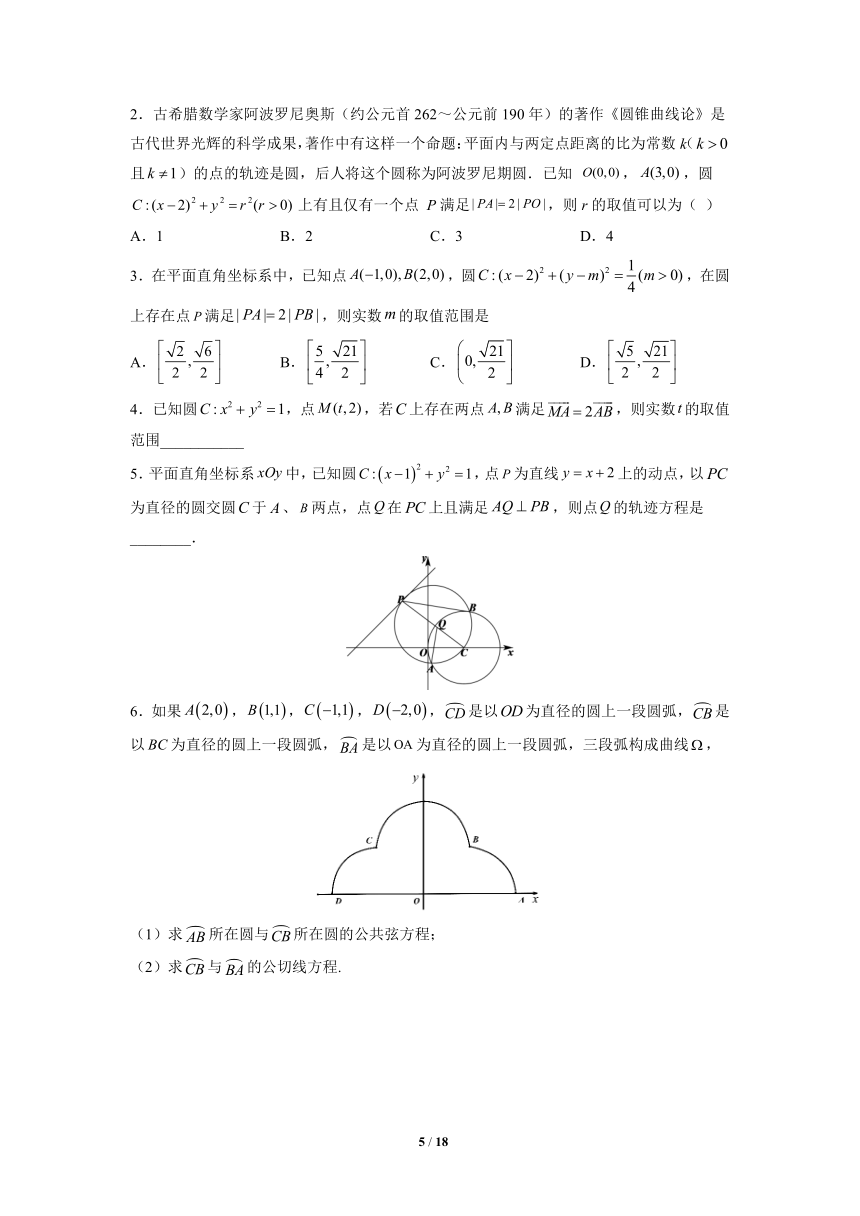
5.平面直角坐标系中,已知圆,点为直线上的动点,以为直径的圆交圆于、两点,点在上且满足,则点的轨迹方程是________.
6.如果,,,,是以为直径的圆上一段圆弧,是以为直径的圆上一段圆弧,是以为直径的圆上一段圆弧,三段弧构成曲线,
(1)求所在圆与所在圆的公共弦方程;
(2)求与的公切线方程.
第1章 直线与方程
第01讲 直线的斜率与倾斜角答案
课程标准 重难点
1.能根据给定圆的方程,判断圆与圆的位置关系.2.能用直线和圆的方程解决一些简单的问题,体会用代数方法处理几何问题的思想. 1.根据圆与圆的位置关系确定两者之间的公切线个数2.公共弦方程
知识点一 圆与圆的位置关系
1.圆与圆的位置关系
圆与圆的位置关系有五种,分别为相离、外切、相交、内切、内含.
2.圆与圆位置关系的判定
(1)几何法:若两圆的半径分别为r1、r2,两圆连心线的长为d,则两圆的位置关系的判断方法如下:
位置关系 外离 外切 相交 内切 内含
图示
d与r1、r2的关系 d>r1+r2 d=r1+r2 |r1-r2|<d<r1+r2 d=|r1-r2| d<|r1-r2|
(2)代数法:设两圆的一般方程为
C1:x2+y2+D1x+E1y+F1=0(D+E-4F1>0),
C2:x2+y2+D2x+E2y+F2=0(D+E-4F2>0),
联立方程得
则方程组解的个数与两圆的位置关系如下:
方程组解的个数 2组 1组 0组
两圆的公共点个数 2个 1个 0个
两圆的位置关系 相交 内切或外切 外离或内含
3.【概念解读】
几何法是利用两圆半径的和或差与圆心距作比较得到两圆的位置关系,代数法则是把两圆位置关系的判定完全转化为代数问题,即方程组的解的个数问题,但这种代数判定方法只能判断出不相交、相交、相切三种位置关系,而不能像几何判定方法一样,能判定出外离、外切、相交、内切、内含五种位置关系,因此一般情况下,使用几何法判定两圆的位置关系问题.
考法01 圆与圆的位置关系
设直线过原点,其倾斜角为,将直线绕坐标原点沿逆时针方向旋转45°,得到直线,则直线1的倾斜角为
【答案】当0°≤<135°时,为+45°,当135°≤<180°时,为-135°
【解析】倾斜角的范围是[0°,180°),因此,只有当+45°∈[0°,180°),即当0°≤<135°时,的倾斜角才是+45°,而当135°≤<180°时,的倾斜角为-135°.故应选D.
【跟踪训练】
1.如果圆C:x2+y2-2ax-2ay+2a2-4=0与圆O:x2+y2=4总相交,那么实数a的取值范围是_________________.
【答案】(-2,0)∪(0,2)
【解析】圆C的标准方程为(x-a)2+(y-a)2=4,
圆心坐标为(a,a),半径为2.
依题意得0<<4,
∴0<|a|<2.∴a∈(-2,0)∪(0,2).
2.已知两圆x2+y2-2x-6y-1=0,x2+y2-10x-12y+m=0.
(1)m取何值时两圆外切?
(2)m取何值时两圆内切?
(3)当m=45时,求两圆的公共弦所在直线的方程和公共弦的长.
【解析】因为两圆的标准方程分别为(x-1)2+(y-3)2=11,
(x-5)2+(y-6)2=61-m,
所以两圆的圆心分别为(1,3),(5,6),半径分别为,,
(1)当两圆外切时,由=+,得m=25+10.
(2)当两圆内切时,因为定圆半径小于两圆圆心之间的距离5,所以-=5,解得m=25-10.
(3)由(x2+y2-2x-6y-1)-(x2+y2-10x-12y+45)=0,得两圆的公共弦所在直线的方程为4x+3y-23=0.
故两圆的公共弦的长为
2 .
【方法总结】
(1)判断两圆的位置关系时常用几何法,即利用两圆圆心之间的距离与两圆半径之间的关系,一般不采用代数法.
(2)若两圆相交,则两圆公共弦所在直线的方程可由两圆的方程作差消去x2,y2项得到.
题组A 基础过关练
1.若圆与圆相交于A,B两点,且两圆在点A处的切线互相垂直,则线段的长是( )
A. B. C.4 D.
【答案】C
【解析】由题意作出图形分析得:
由圆的几何性质知:当两圆在点A处的切线互相垂直时,切线分别过对方圆心、,
则在中,,,所以,
斜边上的高为半弦,且,
则,即,所以.
故选:C.
2.圆和圆的公共弦的垂直平分线的方程是( )
A. B.
C. D.
【答案】C
【解析】圆的圆心,
圆的圆心,
所以的中点坐标为,,即,
所以两圆的公共弦的垂直平分线即是圆心所在的直线:,即,
故选:.
3.圆和圆的位置关系为( )
A.内切 B.相交
C.外切 D.外离
【答案】C
【解析】因为圆的方程为,所以圆心,半径,
因为圆的方程为,所以圆心,半径,
所以.
因为,所以圆和圆外切.故选:C.
4.已知圆,圆,则两圆的公切线的条数是( )
A.1条 B.2条 C.3条 D.4条
【答案】B
【解析】由圆可化为,
可得圆心坐标为,半径为,
由圆可化为,
可得圆心坐标为,半径为,
则圆心距为,
又由,所以,
可得圆与圆相交,所以两圆公共切线的条数为2条.
故选:B.
5.直线被圆截得的弦长为,则实数______;圆与圆的公共弦所在直线方程是______.
【答案】-1
【解析】的圆心为,半径为,圆心到直线的距离为,
所以,由于,故解得.
所以,
,
故公共弦所在直线方程为.
故答案为:;
6.两圆与的公切线有___________条.
【答案】3
【解析】圆整理可得:,可得圆心的坐标为:,半径;
的圆心坐标, 半径;
所以圆心距,
所以可得两个圆外切,所以公切线有3条,
故答案为:3.
7.在平面直角坐标系中,若圆和圆关于直线对称,则直线的方程为________.
【答案】
【解析】若圆和圆关于直线对称,
则直线为两个圆心的中垂线,
的圆心为,
的圆心为.
,中点为
可得直线为 ,整理得:.
故答案为:.
8.若圆x2+y2=r2与圆x2+y2+2x-4y+4=0有公共点,则r满足的条件是________.
【答案】|r-|≤1
【解析】由x2+y2+2x-4y+4=0,得(x+1)2+(y-2)2=1,
两圆圆心之间的距离为=.
因为两圆有公共点,所以|r-1|≤≤r+1,-1≤r≤+1,
即-1≤r-≤1,所以|r-|≤1.
故答案为: |r-|≤1
题组B 能力提升练
1.已知圆,,则这两圆的公共弦长为( )
A.2 B. C.2 D.1
【答案】C
【解析】由题意知,,将两圆的方程相减,得,所以两圆的公共弦所在直线的方程为.
又因为圆的圆心为,半径,所以圆的圆心到直线的距离.所以这两圆的公共弦的弦长为.
故选:C.
2.过点作直线与圆相切于、两点,则直线的方程为( )
A. B. C. D.
【答案】B
【解析】圆的标准方程为,圆心为,半径为,
由圆的切线的性质可得,则,
所以,以点为圆心、以为半径的圆的方程为,
将圆的方程与圆的方程作差并化简可得.
因此,直线的方程为.故选:B.
3.已知两圆相交于两点,,两圆圆心都在直线上,则的值为( )
A. B. C. D.
【答案】A
【解析】根据题意,由相交弦的性质,相交两圆的连心线垂直平分相交弦,
可得与直线垂直,且的中点在这条直线上;
由与直线垂直,可得,解可得,
则,
故中点为,且其在直线上,
代入直线方程可得,1,可得;
故;故选:A
4.已知圆与圆的公共弦所在直线恒过点,且点在直线上,则的取值范围是( )
A. B. C. D.
【答案】A
【解析】由圆,圆,
得圆与圆的公共弦所在直线方程为,求得定点,
又在直线上,,即.
∴,∴的取值范围是.故选:A.
5.圆和圆只有一条公切线,若,,且,则的最小值为___________.
【答案】
【解析】因为圆和圆,所以圆和圆,圆心分别为,,半径分别为和,依题意可知两圆相内切,所以,所以,因为,,且,
所以,当且仅当时,等号成立,所以的最小值为;
故答案为:
6.已知半径为5的动圆的圆心在直线:上.存在正实数___________,使得动圆中满足与圆:相外切的圆有且仅有一个.
【答案】
【解析】原点到直线的距离,
当满足时,即时,
动圆中有且仅有1个圆与圆:相外切.
故答案为:
7.已知圆C1:(x-a)2+(y+2)2=4与圆C2:(x+b)2+(y+2)2=1外切,则ab的最大值为_____________.
【答案】
【解析】由两圆外切可得圆心(a,-2),(-b,-2)之间的距离等于两圆半径之和,
即(a+b)2=(2+1)2,即9=a2+b2+2ab≥4ab,所以ab≤,
当且仅当a=b时取等号,即ab的最大值是.
故答案为:
8.(1)直线经过两直线和的交点,且直线与直线垂直,求直线的方程;
(2)已知以为圆心的圆与圆O:相切,求圆的方程.
【解析】(1)由 得,即交点坐标为,
又因为直线与直线垂直,
所以直线的斜率为,
则直线的方程为,即;
(2)设圆的半径为,
两圆的圆心距为,
因为两圆相切,所以或,则或,
所以所求圆的方程为:
或.
题组C 培优拔尖练
1.过圆内一点作直线交圆O于A,B两点,过A,B分别作圆的切线交于点P,则点P的坐标满足方程( )
A. B. C. D.
【答案】A
【解析】设,则以为直径的圆,即①
因为是圆O的切线,所以,所以A,B在圆M上,
所以是圆O与圆M的公共弦,又因为圆②,
所以由①②得直线的方程为:,
又点满足直线方程,所以,即.
故选:A.
2.古希腊数学家阿波罗尼奥斯(约公元首262~公元前190年)的著作《圆锥曲线论》是古代世界光辉的科学成果,著作中有这样一个命题:平面内与两定点距离的比为常数k(且)的点的轨迹是圆,后人将这个圆称为阿波罗尼期圆.已知 ,,圆上有且仅有一个点 P满足,则r的取值可以为( )
A.1 B.2 C.3 D.4
【答案】A
【解析】设动点,由,得,整理得,
又点是圆:上有且仅有的一点,所以两圆相切.
圆的圆心坐标为,半径为2,
圆C:的圆心坐标为,半径为r,两圆的圆心距为3,
当两圆外切时,,得,
当两圆内切时,,,得.故选:A.
3.在平面直角坐标系中,已知点,圆,在圆上存在点满足,则实数的取值范围是
A. B. C. D.
【答案】D
【解析】设点,由可得
化简得即点的轨迹是圆心为,半径为的圆,
因为点在圆上,所以圆和有公共点,
所以,
,又,所以故选:D
4.已知圆,点,若上存在两点满足,则实数的取值范围___________
【答案】
【解析】由题意,可得如下示意图,
令,由知:,又在上,
∴,整理得,即两圆有公共点,
∴两圆的圆心距离为,半径分别为、,故当时符合题意,
∴,即.
故答案为:.
5.平面直角坐标系中,已知圆,点为直线上的动点,以为直径的圆交圆于、两点,点在上且满足,则点的轨迹方程是________.
【答案】
【解析】延长交于点,则,设,
以为直径的圆交圆于点、,所以,,
则,可得,
在和中,,,,
,,,,
,,,则为的中点,且,
,,,则为的中点,
设点,则,,
的中点坐标为,
以线段为直径的圆的方程为,
即,
将圆与圆的方程相减得,
即直线的方程为,即,
由,解得,所以,直线过定点,
由于为线段的垂直平分线,则,
所以,点的轨迹方程为.
故答案为:.
6.如果,,,,是以为直径的圆上一段圆弧,是以为直径的圆上一段圆弧,是以为直径的圆上一段圆弧,三段弧构成曲线,
(1)求所在圆与所在圆的公共弦方程;
(2)求与的公切线方程.
【解析】(1)所在的圆是以为圆心,半径为的圆,
所以所在圆的方程为,
所在的圆是以为圆心,半径为的圆,
所以所在圆的方程为,
两圆的方程相减可得:即;
(2)因为所在的圆是以为圆心,半径为的圆,
所在的圆是以为圆心,半径为的圆,
所以与所在圆的的公切线平行于经过点、的直线,
所以所求切线的斜率为,
设公切线的方程为,
则点到的距离,
解得:或(舍)
所以公切线的方程为.
目标导航
知识精讲
能力拓展
例 1
分层提分
目标导航
知识精讲
能力拓展
例 1
分层提分
5 / 18
第01讲 直线的斜率与倾斜角
课程标准 重难点
1.能根据给定圆的方程,判断圆与圆的位置关系.2.能用直线和圆的方程解决一些简单的问题,体会用代数方法处理几何问题的思想. 1.根据圆与圆的位置关系确定两者之间的公切线个数2.公共弦方程
知识点一 圆与圆的位置关系
1.圆与圆的位置关系
圆与圆的位置关系有五种,分别为相离、外切、相交、内切、内含.
2.圆与圆位置关系的判定
(1)几何法:若两圆的半径分别为r1、r2,两圆连心线的长为d,则两圆的位置关系的判断方法如下:
位置关系 外离 外切 相交 内切 内含
图示
d与r1、r2的关系 d>r1+r2 d=r1+r2 |r1-r2|<d<r1+r2 d=|r1-r2| d<|r1-r2|
(2)代数法:设两圆的一般方程为
C1:x2+y2+D1x+E1y+F1=0(D+E-4F1>0),
C2:x2+y2+D2x+E2y+F2=0(D+E-4F2>0),
联立方程得
则方程组解的个数与两圆的位置关系如下:
方程组解的个数 2组 1组 0组
两圆的公共点个数 2个 1个 0个
两圆的位置关系 相交 内切或外切 外离或内含
3.【概念解读】
几何法是利用两圆半径的和或差与圆心距作比较得到两圆的位置关系,代数法则是把两圆位置关系的判定完全转化为代数问题,即方程组的解的个数问题,但这种代数判定方法只能判断出不相交、相交、相切三种位置关系,而不能像几何判定方法一样,能判定出外离、外切、相交、内切、内含五种位置关系,因此一般情况下,使用几何法判定两圆的位置关系问题.
考法01 圆与圆的位置关系
设直线过原点,其倾斜角为,将直线绕坐标原点沿逆时针方向旋转45°,得到直线,则直线1的倾斜角为
【跟踪训练】
1.如果圆C:x2+y2-2ax-2ay+2a2-4=0与圆O:x2+y2=4总相交,那么实数a的取值范围是_________________.
【答案】(-2,0)∪(0,2)
【解析】圆C的标准方程为(x-a)2+(y-a)2=4,
圆心坐标为(a,a),半径为2.
依题意得0<<4,
∴0<|a|<2.∴a∈(-2,0)∪(0,2).
2.已知两圆x2+y2-2x-6y-1=0,x2+y2-10x-12y+m=0.
(1)m取何值时两圆外切?
(2)m取何值时两圆内切?
(3)当m=45时,求两圆的公共弦所在直线的方程和公共弦的长.
【方法总结】
(1)判断两圆的位置关系时常用几何法,即利用两圆圆心之间的距离与两圆半径之间的关系,一般不采用代数法.
(2)若两圆相交,则两圆公共弦所在直线的方程可由两圆的方程作差消去x2,y2项得到.
题组A 基础过关练
1.若圆与圆相交于A,B两点,且两圆在点A处的切线互相垂直,则线段的长是( )
A. B. C.4 D.
2.圆和圆的公共弦的垂直平分线的方程是( )
A. B.
C. D.
3.圆和圆的位置关系为( )
A.内切 B.相交
C.外切 D.外离
4.已知圆,圆,则两圆的公切线的条数是( )
A.1条 B.2条 C.3条 D.4条
5.直线被圆截得的弦长为,则实数______;圆与圆的公共弦所在直线方程是______.
6.两圆与的公切线有___________条.
7.在平面直角坐标系中,若圆和圆关于直线对称,则直线的方程为________.
8.若圆x2+y2=r2与圆x2+y2+2x-4y+4=0有公共点,则r满足的条件是________.
题组B 能力提升练
1.已知圆,,则这两圆的公共弦长为( )
A.2 B. C.2 D.1
2.过点作直线与圆相切于、两点,则直线的方程为( )
A. B. C. D.
3.已知两圆相交于两点,,两圆圆心都在直线上,则的值为( )
A. B. C. D.
4.已知圆与圆的公共弦所在直线恒过点,且点在直线上,则的取值范围是( )
A. B. C. D.
5.圆和圆只有一条公切线,若,,且,则的最小值为___________.
6.已知半径为5的动圆的圆心在直线:上.存在正实数___________,使得动圆中满足与圆:相外切的圆有且仅有一个.
7.已知圆C1:(x-a)2+(y+2)2=4与圆C2:(x+b)2+(y+2)2=1外切,则ab的最大值为_____________.
8.(1)直线经过两直线和的交点,且直线与直线垂直,求直线的方程;
(2)已知以为圆心的圆与圆O:相切,求圆的方程.
题组C 培优拔尖练
1.过圆内一点作直线交圆O于A,B两点,过A,B分别作圆的切线交于点P,则点P的坐标满足方程( )
A. B. C. D.
2.古希腊数学家阿波罗尼奥斯(约公元首262~公元前190年)的著作《圆锥曲线论》是古代世界光辉的科学成果,著作中有这样一个命题:平面内与两定点距离的比为常数k(且)的点的轨迹是圆,后人将这个圆称为阿波罗尼期圆.已知 ,,圆上有且仅有一个点 P满足,则r的取值可以为( )
A.1 B.2 C.3 D.4
3.在平面直角坐标系中,已知点,圆,在圆上存在点满足,则实数的取值范围是
A. B. C. D.
4.已知圆,点,若上存在两点满足,则实数的取值范围___________
5.平面直角坐标系中,已知圆,点为直线上的动点,以为直径的圆交圆于、两点,点在上且满足,则点的轨迹方程是________.
6.如果,,,,是以为直径的圆上一段圆弧,是以为直径的圆上一段圆弧,是以为直径的圆上一段圆弧,三段弧构成曲线,
(1)求所在圆与所在圆的公共弦方程;
(2)求与的公切线方程.
第1章 直线与方程
第01讲 直线的斜率与倾斜角答案
课程标准 重难点
1.能根据给定圆的方程,判断圆与圆的位置关系.2.能用直线和圆的方程解决一些简单的问题,体会用代数方法处理几何问题的思想. 1.根据圆与圆的位置关系确定两者之间的公切线个数2.公共弦方程
知识点一 圆与圆的位置关系
1.圆与圆的位置关系
圆与圆的位置关系有五种,分别为相离、外切、相交、内切、内含.
2.圆与圆位置关系的判定
(1)几何法:若两圆的半径分别为r1、r2,两圆连心线的长为d,则两圆的位置关系的判断方法如下:
位置关系 外离 外切 相交 内切 内含
图示
d与r1、r2的关系 d>r1+r2 d=r1+r2 |r1-r2|<d<r1+r2 d=|r1-r2| d<|r1-r2|
(2)代数法:设两圆的一般方程为
C1:x2+y2+D1x+E1y+F1=0(D+E-4F1>0),
C2:x2+y2+D2x+E2y+F2=0(D+E-4F2>0),
联立方程得
则方程组解的个数与两圆的位置关系如下:
方程组解的个数 2组 1组 0组
两圆的公共点个数 2个 1个 0个
两圆的位置关系 相交 内切或外切 外离或内含
3.【概念解读】
几何法是利用两圆半径的和或差与圆心距作比较得到两圆的位置关系,代数法则是把两圆位置关系的判定完全转化为代数问题,即方程组的解的个数问题,但这种代数判定方法只能判断出不相交、相交、相切三种位置关系,而不能像几何判定方法一样,能判定出外离、外切、相交、内切、内含五种位置关系,因此一般情况下,使用几何法判定两圆的位置关系问题.
考法01 圆与圆的位置关系
设直线过原点,其倾斜角为,将直线绕坐标原点沿逆时针方向旋转45°,得到直线,则直线1的倾斜角为
【答案】当0°≤<135°时,为+45°,当135°≤<180°时,为-135°
【解析】倾斜角的范围是[0°,180°),因此,只有当+45°∈[0°,180°),即当0°≤<135°时,的倾斜角才是+45°,而当135°≤<180°时,的倾斜角为-135°.故应选D.
【跟踪训练】
1.如果圆C:x2+y2-2ax-2ay+2a2-4=0与圆O:x2+y2=4总相交,那么实数a的取值范围是_________________.
【答案】(-2,0)∪(0,2)
【解析】圆C的标准方程为(x-a)2+(y-a)2=4,
圆心坐标为(a,a),半径为2.
依题意得0<<4,
∴0<|a|<2.∴a∈(-2,0)∪(0,2).
2.已知两圆x2+y2-2x-6y-1=0,x2+y2-10x-12y+m=0.
(1)m取何值时两圆外切?
(2)m取何值时两圆内切?
(3)当m=45时,求两圆的公共弦所在直线的方程和公共弦的长.
【解析】因为两圆的标准方程分别为(x-1)2+(y-3)2=11,
(x-5)2+(y-6)2=61-m,
所以两圆的圆心分别为(1,3),(5,6),半径分别为,,
(1)当两圆外切时,由=+,得m=25+10.
(2)当两圆内切时,因为定圆半径小于两圆圆心之间的距离5,所以-=5,解得m=25-10.
(3)由(x2+y2-2x-6y-1)-(x2+y2-10x-12y+45)=0,得两圆的公共弦所在直线的方程为4x+3y-23=0.
故两圆的公共弦的长为
2 .
【方法总结】
(1)判断两圆的位置关系时常用几何法,即利用两圆圆心之间的距离与两圆半径之间的关系,一般不采用代数法.
(2)若两圆相交,则两圆公共弦所在直线的方程可由两圆的方程作差消去x2,y2项得到.
题组A 基础过关练
1.若圆与圆相交于A,B两点,且两圆在点A处的切线互相垂直,则线段的长是( )
A. B. C.4 D.
【答案】C
【解析】由题意作出图形分析得:
由圆的几何性质知:当两圆在点A处的切线互相垂直时,切线分别过对方圆心、,
则在中,,,所以,
斜边上的高为半弦,且,
则,即,所以.
故选:C.
2.圆和圆的公共弦的垂直平分线的方程是( )
A. B.
C. D.
【答案】C
【解析】圆的圆心,
圆的圆心,
所以的中点坐标为,,即,
所以两圆的公共弦的垂直平分线即是圆心所在的直线:,即,
故选:.
3.圆和圆的位置关系为( )
A.内切 B.相交
C.外切 D.外离
【答案】C
【解析】因为圆的方程为,所以圆心,半径,
因为圆的方程为,所以圆心,半径,
所以.
因为,所以圆和圆外切.故选:C.
4.已知圆,圆,则两圆的公切线的条数是( )
A.1条 B.2条 C.3条 D.4条
【答案】B
【解析】由圆可化为,
可得圆心坐标为,半径为,
由圆可化为,
可得圆心坐标为,半径为,
则圆心距为,
又由,所以,
可得圆与圆相交,所以两圆公共切线的条数为2条.
故选:B.
5.直线被圆截得的弦长为,则实数______;圆与圆的公共弦所在直线方程是______.
【答案】-1
【解析】的圆心为,半径为,圆心到直线的距离为,
所以,由于,故解得.
所以,
,
故公共弦所在直线方程为.
故答案为:;
6.两圆与的公切线有___________条.
【答案】3
【解析】圆整理可得:,可得圆心的坐标为:,半径;
的圆心坐标, 半径;
所以圆心距,
所以可得两个圆外切,所以公切线有3条,
故答案为:3.
7.在平面直角坐标系中,若圆和圆关于直线对称,则直线的方程为________.
【答案】
【解析】若圆和圆关于直线对称,
则直线为两个圆心的中垂线,
的圆心为,
的圆心为.
,中点为
可得直线为 ,整理得:.
故答案为:.
8.若圆x2+y2=r2与圆x2+y2+2x-4y+4=0有公共点,则r满足的条件是________.
【答案】|r-|≤1
【解析】由x2+y2+2x-4y+4=0,得(x+1)2+(y-2)2=1,
两圆圆心之间的距离为=.
因为两圆有公共点,所以|r-1|≤≤r+1,-1≤r≤+1,
即-1≤r-≤1,所以|r-|≤1.
故答案为: |r-|≤1
题组B 能力提升练
1.已知圆,,则这两圆的公共弦长为( )
A.2 B. C.2 D.1
【答案】C
【解析】由题意知,,将两圆的方程相减,得,所以两圆的公共弦所在直线的方程为.
又因为圆的圆心为,半径,所以圆的圆心到直线的距离.所以这两圆的公共弦的弦长为.
故选:C.
2.过点作直线与圆相切于、两点,则直线的方程为( )
A. B. C. D.
【答案】B
【解析】圆的标准方程为,圆心为,半径为,
由圆的切线的性质可得,则,
所以,以点为圆心、以为半径的圆的方程为,
将圆的方程与圆的方程作差并化简可得.
因此,直线的方程为.故选:B.
3.已知两圆相交于两点,,两圆圆心都在直线上,则的值为( )
A. B. C. D.
【答案】A
【解析】根据题意,由相交弦的性质,相交两圆的连心线垂直平分相交弦,
可得与直线垂直,且的中点在这条直线上;
由与直线垂直,可得,解可得,
则,
故中点为,且其在直线上,
代入直线方程可得,1,可得;
故;故选:A
4.已知圆与圆的公共弦所在直线恒过点,且点在直线上,则的取值范围是( )
A. B. C. D.
【答案】A
【解析】由圆,圆,
得圆与圆的公共弦所在直线方程为,求得定点,
又在直线上,,即.
∴,∴的取值范围是.故选:A.
5.圆和圆只有一条公切线,若,,且,则的最小值为___________.
【答案】
【解析】因为圆和圆,所以圆和圆,圆心分别为,,半径分别为和,依题意可知两圆相内切,所以,所以,因为,,且,
所以,当且仅当时,等号成立,所以的最小值为;
故答案为:
6.已知半径为5的动圆的圆心在直线:上.存在正实数___________,使得动圆中满足与圆:相外切的圆有且仅有一个.
【答案】
【解析】原点到直线的距离,
当满足时,即时,
动圆中有且仅有1个圆与圆:相外切.
故答案为:
7.已知圆C1:(x-a)2+(y+2)2=4与圆C2:(x+b)2+(y+2)2=1外切,则ab的最大值为_____________.
【答案】
【解析】由两圆外切可得圆心(a,-2),(-b,-2)之间的距离等于两圆半径之和,
即(a+b)2=(2+1)2,即9=a2+b2+2ab≥4ab,所以ab≤,
当且仅当a=b时取等号,即ab的最大值是.
故答案为:
8.(1)直线经过两直线和的交点,且直线与直线垂直,求直线的方程;
(2)已知以为圆心的圆与圆O:相切,求圆的方程.
【解析】(1)由 得,即交点坐标为,
又因为直线与直线垂直,
所以直线的斜率为,
则直线的方程为,即;
(2)设圆的半径为,
两圆的圆心距为,
因为两圆相切,所以或,则或,
所以所求圆的方程为:
或.
题组C 培优拔尖练
1.过圆内一点作直线交圆O于A,B两点,过A,B分别作圆的切线交于点P,则点P的坐标满足方程( )
A. B. C. D.
【答案】A
【解析】设,则以为直径的圆,即①
因为是圆O的切线,所以,所以A,B在圆M上,
所以是圆O与圆M的公共弦,又因为圆②,
所以由①②得直线的方程为:,
又点满足直线方程,所以,即.
故选:A.
2.古希腊数学家阿波罗尼奥斯(约公元首262~公元前190年)的著作《圆锥曲线论》是古代世界光辉的科学成果,著作中有这样一个命题:平面内与两定点距离的比为常数k(且)的点的轨迹是圆,后人将这个圆称为阿波罗尼期圆.已知 ,,圆上有且仅有一个点 P满足,则r的取值可以为( )
A.1 B.2 C.3 D.4
【答案】A
【解析】设动点,由,得,整理得,
又点是圆:上有且仅有的一点,所以两圆相切.
圆的圆心坐标为,半径为2,
圆C:的圆心坐标为,半径为r,两圆的圆心距为3,
当两圆外切时,,得,
当两圆内切时,,,得.故选:A.
3.在平面直角坐标系中,已知点,圆,在圆上存在点满足,则实数的取值范围是
A. B. C. D.
【答案】D
【解析】设点,由可得
化简得即点的轨迹是圆心为,半径为的圆,
因为点在圆上,所以圆和有公共点,
所以,
,又,所以故选:D
4.已知圆,点,若上存在两点满足,则实数的取值范围___________
【答案】
【解析】由题意,可得如下示意图,
令,由知:,又在上,
∴,整理得,即两圆有公共点,
∴两圆的圆心距离为,半径分别为、,故当时符合题意,
∴,即.
故答案为:.
5.平面直角坐标系中,已知圆,点为直线上的动点,以为直径的圆交圆于、两点,点在上且满足,则点的轨迹方程是________.
【答案】
【解析】延长交于点,则,设,
以为直径的圆交圆于点、,所以,,
则,可得,
在和中,,,,
,,,,
,,,则为的中点,且,
,,,则为的中点,
设点,则,,
的中点坐标为,
以线段为直径的圆的方程为,
即,
将圆与圆的方程相减得,
即直线的方程为,即,
由,解得,所以,直线过定点,
由于为线段的垂直平分线,则,
所以,点的轨迹方程为.
故答案为:.
6.如果,,,,是以为直径的圆上一段圆弧,是以为直径的圆上一段圆弧,是以为直径的圆上一段圆弧,三段弧构成曲线,
(1)求所在圆与所在圆的公共弦方程;
(2)求与的公切线方程.
【解析】(1)所在的圆是以为圆心,半径为的圆,
所以所在圆的方程为,
所在的圆是以为圆心,半径为的圆,
所以所在圆的方程为,
两圆的方程相减可得:即;
(2)因为所在的圆是以为圆心,半径为的圆,
所在的圆是以为圆心,半径为的圆,
所以与所在圆的的公切线平行于经过点、的直线,
所以所求切线的斜率为,
设公切线的方程为,
则点到的距离,
解得:或(舍)
所以公切线的方程为.
目标导航
知识精讲
能力拓展
例 1
分层提分
目标导航
知识精讲
能力拓展
例 1
分层提分
5 / 18
