北师大版九年级数学下册 3.6 直线和圆的位置关系 课时练(含答案)
文档属性
| 名称 | 北师大版九年级数学下册 3.6 直线和圆的位置关系 课时练(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 172.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-29 09:33:48 | ||
图片预览


文档简介
课 时 练
第3单元 圆
6 直线和圆的位置关系
一、基础训练
1. [2021江苏扬州江都区期中]已知☉O的直径为4,圆心O到直线l的距离是3,则直线l与☉O的位置关系是 ( )
A.相切 B.相离
C.相交 D.无法确定
2. [2021山东济宁兖州区期末]在Rt△ABC中,∠C=90°,BC=3 cm,AC=4 cm,以点C为圆心,以2.5 cm为半径画圆,则☉C与直线AB的位置关系是 ( )
A.相交 B.相切
C.相离 D.不能确定
3. [2020湖北武汉模拟]已知☉O的半径为8 cm,圆心O到直线l上某点的距离为8 cm,则直线l与☉O的公共点个数为 ( )
A.0 B.0或1 C.0或2 D.1或2
4. [2021浙江杭州中考改编]如图,已知☉O的半径为1,点P是☉O外一点,且OP=2.若PT是☉O的切线,T为切点,连接OT,则PT= ( )
A. B. C.1 D.2
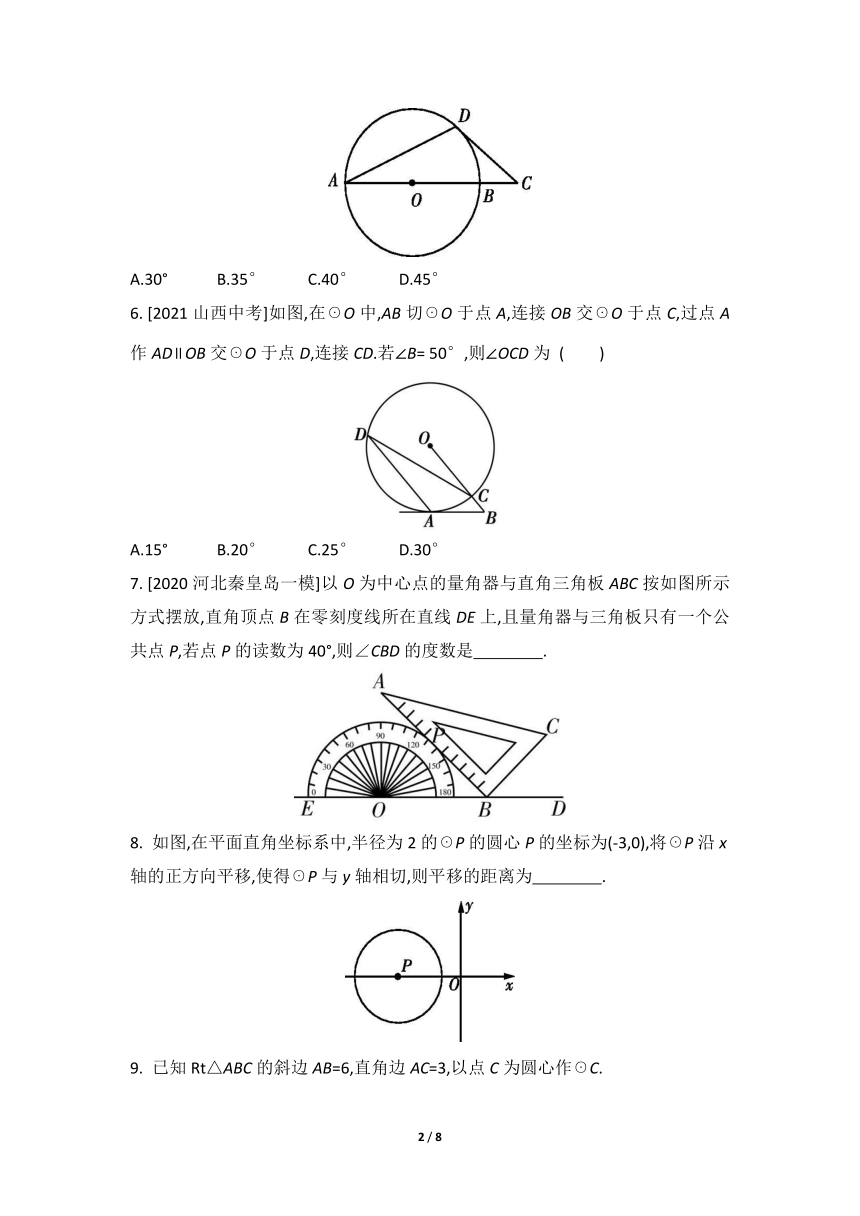
5. [2021黑龙江哈尔滨道外区二模]如图,AB为☉O的直径,C为AB延长线上一点,过点C作☉O的切线CD,切点为D,若∠ADC=115°,则∠C的度数为( )
A.30° B.35° C.40° D.45°
6. [2021山西中考]如图,在☉O中,AB切☉O于点A,连接OB交☉O于点C,过点A作AD∥OB交☉O于点D,连接CD.若∠B= 50°,则∠OCD为 ( )
A.15° B.20° C.25° D.30°
7. [2020河北秦皇岛一模]以O为中心点的量角器与直角三角板ABC按如图所示方式摆放,直角顶点B在零刻度线所在直线DE上,且量角器与三角板只有一个公共点P,若点P的读数为40°,则∠CBD的度数是 .
8. 如图,在平面直角坐标系中,半径为2的☉P的圆心P的坐标为(-3,0),将☉P沿x轴的正方向平移,使得☉P与y轴相切,则平移的距离为 .
9. 已知Rt△ABC的斜边AB=6,直角边AC=3,以点C为圆心作☉C.
(1)当半径r为 时,直线AB与☉C相切;
(2)当☉C与线段AB只有一个公共点时,半径r的取值范围为 ;
(3)当☉C与线段AB没有公共点时,半径r的取值范围为 .
10. 如图,AC是☉O的直径,AB是☉O的一条弦,AP是☉O的切线.作BM=AB并与AP交于点M,延长MB交AC于点E,交☉O于点D,连接AD.
(1)求证:AB=BE.
(2)若☉O的半径R=5,AB=6,求AD的长.
二、提升训练
1. [2021湖南衡阳模拟]如图,AB是☉O的直径,PA切☉O于点A,连接PO并延长交☉O于点C,连接AC,若AB=10,∠P=30°,则AC的长是 ( )
A.5 B.5 C.5 D.
2. [2020河北唐山期末]在平面直角坐标系中,已知点M(4,3),如果以点M为圆心,r为半径的圆与x轴相交,与y轴相离,那么r的取值范围为 ( )
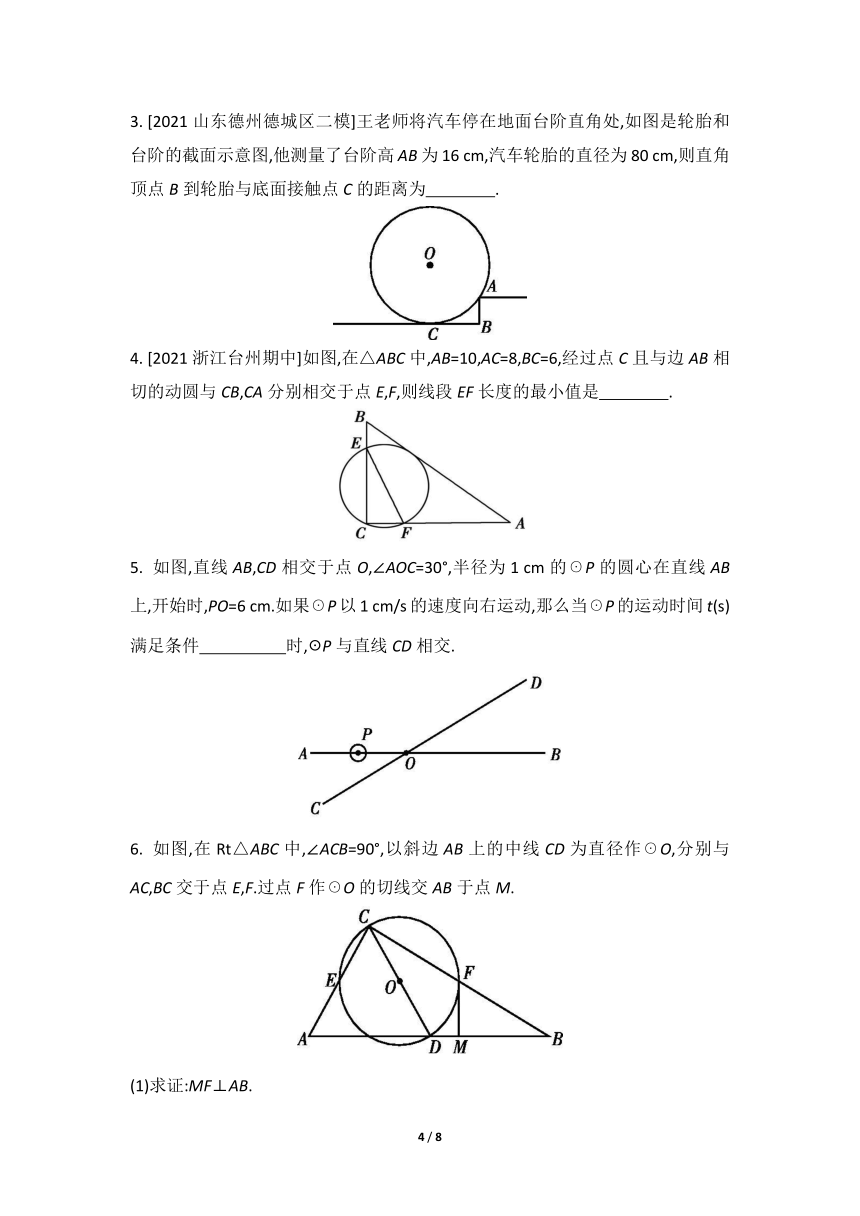
A.0C.43. [2021山东德州德城区二模]王老师将汽车停在地面台阶直角处,如图是轮胎和台阶的截面示意图,他测量了台阶高AB为16 cm,汽车轮胎的直径为80 cm,则直角顶点B到轮胎与底面接触点C的距离为 .
4. [2021浙江台州期中]如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CB,CA分别相交于点E,F,则线段EF长度的最小值是 .
5. 如图,直线AB,CD相交于点O,∠AOC=30°,半径为1 cm的☉P的圆心在直线AB上,开始时,PO=6 cm.如果☉P以1 cm/s的速度向右运动,那么当☉P的运动时间t(s)满足条件 时,☉P与直线CD相交.
6. 如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作☉O,分别与AC,BC交于点E,F.过点F作☉O的切线交AB于点M.
(1)求证:MF⊥AB.
(2)若☉O的直径是6,填空:
①连接OF,OM,当FM= 时,四边形OMBF是平行四边形;
②连接DE,DF,当AC= 时,四边形CEDF是正方形.
7. 如图,点B,C在以AD为直径的☉O上,过点B作☉O的切线,交DA的延长线于点E,连接BD,BC,CD,AC,且AC∥BE.
(1)求证:∠ADB=∠CDB.
(2)若CD=9,tan∠DBC=,求AE的长.
参考答案
一、基础训练
1.B
2.A
3.D
4.A
5.C
6.B
7.40°
8.1或5
9.(1);(2)r=或33
10.(1)∵AP是☉O的切线,∴∠EAM=90°,
∴∠BAE+∠MAB=90°,∠AEB+∠AMB=90°.
∵AB=BM,∴∠MAB=∠AMB,
∴∠BAE=∠AEB,∴AB=BE.
(2)如图,连接BC.
∵AC是☉O的直径,∴∠ABC=90°.
在Rt△ABC中,AC=10,AB=6,∴BC=8.
∵BE=AB=BM,∴EM=12,
由(1)知,∠BAE=∠AEB,∠EAM=90°,
∴△ABC∽△EAM,∴∠C=∠AME,,
∴,∴AM=.
∵∠D=∠C,∴∠D=∠AMD,∴AD=AM=.
二、提升训练
1.A
2.D
3.32 cm
4.4.8
5.46. (1)连接OF,
∵CD是Rt△ABC斜边上的中线,
∴CD=BD,∴∠DCB=∠B.
∵OC=OF,∴∠OCF=∠OFC,
∴∠OFC=∠B,∴OF∥BD,∴∠FMB=∠OFM.
∵FM是☉O的切线,
∴∠OFM=90°,∴∠FMB=90°,即MF⊥AB.
(2)①3
当四边形OMBF是平行四边形时,OF∥AB,OM∥CB.
∵点O是CD的中点,∴点F,M分别是线段CB,DB的中点,
∴FM是△CDB的中位线,∴FM=CD=3.
②6
当四边形CEDF是正方形时,∠DCA=45°.
∵DC=DA,∴∠A=∠DCA=45°,∴∠CDA=90°,
∴AC=CD=6.
7. (1)如图,连接OB,设OB与AC相交于点G.
∵BE为☉O的切线,
∴OB⊥BE,即∠OBE=90°.
∵AC∥BE,∴∠OGA=∠OBE=90°.
∵AD是☉O的直径,
∴∠ACD=90°,∴∠ACD=∠AGO,
∴OB∥CD,∴∠OBD=∠CDB.
∵OB=OD,∴∠ADB=∠OBD,∴∠ADB=∠CDB.
(2)根据题意,得tan∠DAC=tan∠DBC=,
∴,即,解得AC=12.
在Rt△ACD中,由勾股定理得AD==15,
∴OB=OA=.
∵AC∥BE,∴∠DAC=∠E,
∴sin E=sin∠DAC=,
∴,即,
解得OE=,∴AE==5.
8 / 8
第3单元 圆
6 直线和圆的位置关系
一、基础训练
1. [2021江苏扬州江都区期中]已知☉O的直径为4,圆心O到直线l的距离是3,则直线l与☉O的位置关系是 ( )
A.相切 B.相离
C.相交 D.无法确定
2. [2021山东济宁兖州区期末]在Rt△ABC中,∠C=90°,BC=3 cm,AC=4 cm,以点C为圆心,以2.5 cm为半径画圆,则☉C与直线AB的位置关系是 ( )
A.相交 B.相切
C.相离 D.不能确定
3. [2020湖北武汉模拟]已知☉O的半径为8 cm,圆心O到直线l上某点的距离为8 cm,则直线l与☉O的公共点个数为 ( )
A.0 B.0或1 C.0或2 D.1或2
4. [2021浙江杭州中考改编]如图,已知☉O的半径为1,点P是☉O外一点,且OP=2.若PT是☉O的切线,T为切点,连接OT,则PT= ( )
A. B. C.1 D.2
5. [2021黑龙江哈尔滨道外区二模]如图,AB为☉O的直径,C为AB延长线上一点,过点C作☉O的切线CD,切点为D,若∠ADC=115°,则∠C的度数为( )
A.30° B.35° C.40° D.45°
6. [2021山西中考]如图,在☉O中,AB切☉O于点A,连接OB交☉O于点C,过点A作AD∥OB交☉O于点D,连接CD.若∠B= 50°,则∠OCD为 ( )
A.15° B.20° C.25° D.30°
7. [2020河北秦皇岛一模]以O为中心点的量角器与直角三角板ABC按如图所示方式摆放,直角顶点B在零刻度线所在直线DE上,且量角器与三角板只有一个公共点P,若点P的读数为40°,则∠CBD的度数是 .
8. 如图,在平面直角坐标系中,半径为2的☉P的圆心P的坐标为(-3,0),将☉P沿x轴的正方向平移,使得☉P与y轴相切,则平移的距离为 .
9. 已知Rt△ABC的斜边AB=6,直角边AC=3,以点C为圆心作☉C.
(1)当半径r为 时,直线AB与☉C相切;
(2)当☉C与线段AB只有一个公共点时,半径r的取值范围为 ;
(3)当☉C与线段AB没有公共点时,半径r的取值范围为 .
10. 如图,AC是☉O的直径,AB是☉O的一条弦,AP是☉O的切线.作BM=AB并与AP交于点M,延长MB交AC于点E,交☉O于点D,连接AD.
(1)求证:AB=BE.
(2)若☉O的半径R=5,AB=6,求AD的长.
二、提升训练
1. [2021湖南衡阳模拟]如图,AB是☉O的直径,PA切☉O于点A,连接PO并延长交☉O于点C,连接AC,若AB=10,∠P=30°,则AC的长是 ( )
A.5 B.5 C.5 D.
2. [2020河北唐山期末]在平面直角坐标系中,已知点M(4,3),如果以点M为圆心,r为半径的圆与x轴相交,与y轴相离,那么r的取值范围为 ( )
A.0
4. [2021浙江台州期中]如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CB,CA分别相交于点E,F,则线段EF长度的最小值是 .
5. 如图,直线AB,CD相交于点O,∠AOC=30°,半径为1 cm的☉P的圆心在直线AB上,开始时,PO=6 cm.如果☉P以1 cm/s的速度向右运动,那么当☉P的运动时间t(s)满足条件 时,☉P与直线CD相交.
6. 如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作☉O,分别与AC,BC交于点E,F.过点F作☉O的切线交AB于点M.
(1)求证:MF⊥AB.
(2)若☉O的直径是6,填空:
①连接OF,OM,当FM= 时,四边形OMBF是平行四边形;
②连接DE,DF,当AC= 时,四边形CEDF是正方形.
7. 如图,点B,C在以AD为直径的☉O上,过点B作☉O的切线,交DA的延长线于点E,连接BD,BC,CD,AC,且AC∥BE.
(1)求证:∠ADB=∠CDB.
(2)若CD=9,tan∠DBC=,求AE的长.
参考答案
一、基础训练
1.B
2.A
3.D
4.A
5.C
6.B
7.40°
8.1或5
9.(1);(2)r=或3
10.(1)∵AP是☉O的切线,∴∠EAM=90°,
∴∠BAE+∠MAB=90°,∠AEB+∠AMB=90°.
∵AB=BM,∴∠MAB=∠AMB,
∴∠BAE=∠AEB,∴AB=BE.
(2)如图,连接BC.
∵AC是☉O的直径,∴∠ABC=90°.
在Rt△ABC中,AC=10,AB=6,∴BC=8.
∵BE=AB=BM,∴EM=12,
由(1)知,∠BAE=∠AEB,∠EAM=90°,
∴△ABC∽△EAM,∴∠C=∠AME,,
∴,∴AM=.
∵∠D=∠C,∴∠D=∠AMD,∴AD=AM=.
二、提升训练
1.A
2.D
3.32 cm
4.4.8
5.4
∵CD是Rt△ABC斜边上的中线,
∴CD=BD,∴∠DCB=∠B.
∵OC=OF,∴∠OCF=∠OFC,
∴∠OFC=∠B,∴OF∥BD,∴∠FMB=∠OFM.
∵FM是☉O的切线,
∴∠OFM=90°,∴∠FMB=90°,即MF⊥AB.
(2)①3
当四边形OMBF是平行四边形时,OF∥AB,OM∥CB.
∵点O是CD的中点,∴点F,M分别是线段CB,DB的中点,
∴FM是△CDB的中位线,∴FM=CD=3.
②6
当四边形CEDF是正方形时,∠DCA=45°.
∵DC=DA,∴∠A=∠DCA=45°,∴∠CDA=90°,
∴AC=CD=6.
7. (1)如图,连接OB,设OB与AC相交于点G.
∵BE为☉O的切线,
∴OB⊥BE,即∠OBE=90°.
∵AC∥BE,∴∠OGA=∠OBE=90°.
∵AD是☉O的直径,
∴∠ACD=90°,∴∠ACD=∠AGO,
∴OB∥CD,∴∠OBD=∠CDB.
∵OB=OD,∴∠ADB=∠OBD,∴∠ADB=∠CDB.
(2)根据题意,得tan∠DAC=tan∠DBC=,
∴,即,解得AC=12.
在Rt△ACD中,由勾股定理得AD==15,
∴OB=OA=.
∵AC∥BE,∴∠DAC=∠E,
∴sin E=sin∠DAC=,
∴,即,
解得OE=,∴AE==5.
8 / 8
