苏科版九年级数学下册 5.2二次函数的图象和性质 课时练(含答案)
文档属性
| 名称 | 苏科版九年级数学下册 5.2二次函数的图象和性质 课时练(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 74.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-29 09:36:50 | ||
图片预览

文档简介
课时练
5.2二次函数的图象和性质
1.函数的图象的开口_________,对称轴是________,顶点坐标是_______.当x=_______时.y有最_______值_______,当x________时,y随着x的增大而增大;当x_______时,y随着x的增大而减小.
2.函数的图象的开口_________,对称轴是_________,顶点坐标是______,当x=_______时,y有最_______值_______.当x______时,y随着x的增大而增大;当x______时,y随着.x的增大而减小.
3.如果点A(-1,-a)是抛物线y=x2上的一点,那么a=_______.
4.当m=________时,抛物线y=(m-1)xm2-m开口向下.
5.抛物线y=ax2关于x轴对称的抛物线的解析式是______________.
6.已知抛物线的顶点在原点上,对称轴是y轴,且经过点(-2,-2),则抛物线的函数关系式为_________.
7.如图,⊙O的半径为2,C1是函数的图象,C2是函数 的图象,则阴影部分的面积是__________.
8.下列二次函数y=ax2的图象的特征中,与a无关的是 ( )
A.开口方向 B.开口大小
C.最高点的坐标 D.对称轴
9.如图,在同一直角坐标系内画出函数y=ax2和y=ax+3的图象,它们可能是 ( )
10.已知a<-1,点(a-1,y1)、(a,y2)、(a+1,y3)都在函数y=x2的图象上,则 ( )
A.y1<y2<y3 B.y1<y3<y2 C.y3<y2<y1 D.y2<y1<y3
11.二次函数y=3x2,y=-3x2,,的图象的共同点是 ( )
A.都关于原点对称,开口方向向下 B.都关于x轴对称,y随x的增大而增大
C.都关于y轴对称,y随x的增大而减小 D.都关于y轴对称,顶点都是原点
12.在函数①y=3x2;②;③中,图象开口按从大到小的顺序排列的是
( )
A.①>②>③ B.①>③>② C.②>③>① D.②>①>③
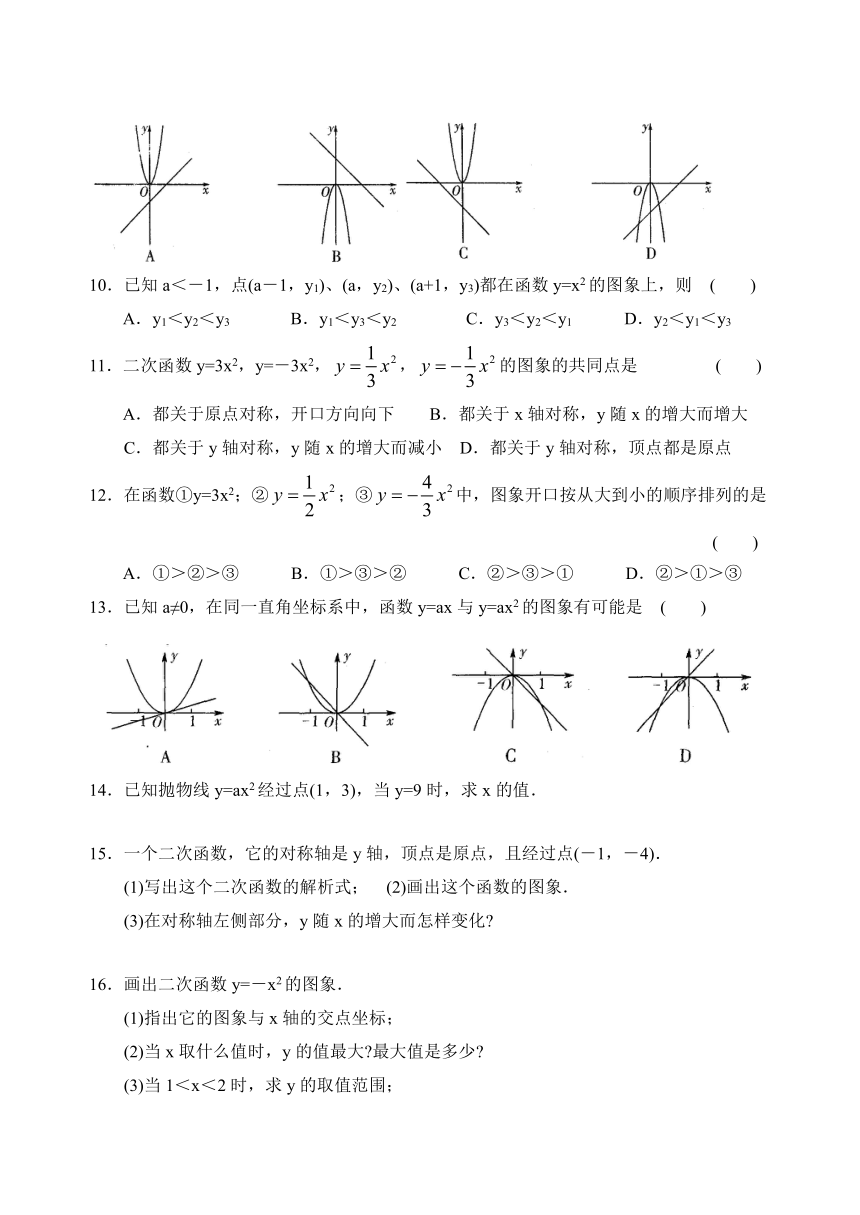
13.已知a≠0,在同一直角坐标系中,函数y=ax与y=ax2的图象有可能是 ( )
14.已知抛物线y=ax2经过点(1,3),当y=9时,求x的值.
15.一个二次函数,它的对称轴是y轴,顶点是原点,且经过点(-1,-4).
(1)写出这个二次函数的解析式; (2)画出这个函数的图象.
(3)在对称轴左侧部分,y随x的增大而怎样变化
16.画出二次函数y=-x2的图象.
(1)指出它的图象与x轴的交点坐标;
(2)当x取什么值时,y的值最大 最大值是多少
(3)当1<x<2时,求y的取值范围;
(4)当-3<x<2时,求y的取值范围.
17.一个函数的图象是以原点为顶点,y轴为对称轴的抛物线,且过点M(2,2).
(1)求出这个函数的关系式,并画出函数图象;
(2)写出抛物线上与点M关于y轴对称的点N的坐标,并求出△MON的面积.
18.二次函数y=ax2与直线y=2x-3交于点P(1,b).
(1)求a,b的值;
(2)写出二次函数的关系式,并指出当x取何值时,y随x的增大而减小
19.如图,已知点P是y=x2上在第一象限内的一点,点A的坐标是(3,0).
(1)设点P的坐标是(x,y),求△OPA的面积S与y的关系式;
(2)S是y的什么函数 S是x的什么函数
20.如图,已知直线过A(4,0)、B(0,4)两点,它与二次函数y=ax2的图象在第一象限内相交于点P.若△AOP的面积为,求a的值.
参考答案
1.向上 y轴 (0,0) 0 小 0 >0 <0
2.向下 y轴 (0,0) 0 大 0 <0 >0
3.-1 4.-1 5.y=-ax2 6.. 7.2
8.D 9.B 10.C 11.D 12.C 13.C
14.把(1,3)代入得a=3,则y=3x2,再把y=9代入y=3x2,得.
15.(1)设二次函数为y=ax2,把(-1,-4)代入上式,得a=-4,则y=-4x2. (2)略
(3)y随x的增大而增大.
16.图略 (1)(0.0) (2)x=0时,y最大=0 (3) -4<y<-1 (4) -9<y<0
17.(1)设y=ax2,把(-2,2)代入y=ax2,得,则,图象略.
(2)N(2,2),.
18.(1)把P(1,b)代入y=2x-3,得b=-1,则P(1,-1),再把P(1,-1)代入y=ax2,得
a=-. (2)y=-x2,当x>0时,y随x的增大而减小.
19.(1) (2)S是y的一次函数,,所以S是x的二次函数.
20.设点P(x,y),直线AB的解析式为y=kx+b,将A(4,0)和B(0,4)分别代入y=kx+b,得k=-1,b=4,则y=-x+4,又因为△AOP的面积为,所以,再把代入y=-x+4,得,所以.再把代入y=ax2,得.
5.2二次函数的图象和性质
1.函数的图象的开口_________,对称轴是________,顶点坐标是_______.当x=_______时.y有最_______值_______,当x________时,y随着x的增大而增大;当x_______时,y随着x的增大而减小.
2.函数的图象的开口_________,对称轴是_________,顶点坐标是______,当x=_______时,y有最_______值_______.当x______时,y随着x的增大而增大;当x______时,y随着.x的增大而减小.
3.如果点A(-1,-a)是抛物线y=x2上的一点,那么a=_______.
4.当m=________时,抛物线y=(m-1)xm2-m开口向下.
5.抛物线y=ax2关于x轴对称的抛物线的解析式是______________.
6.已知抛物线的顶点在原点上,对称轴是y轴,且经过点(-2,-2),则抛物线的函数关系式为_________.
7.如图,⊙O的半径为2,C1是函数的图象,C2是函数 的图象,则阴影部分的面积是__________.
8.下列二次函数y=ax2的图象的特征中,与a无关的是 ( )
A.开口方向 B.开口大小
C.最高点的坐标 D.对称轴
9.如图,在同一直角坐标系内画出函数y=ax2和y=ax+3的图象,它们可能是 ( )
10.已知a<-1,点(a-1,y1)、(a,y2)、(a+1,y3)都在函数y=x2的图象上,则 ( )
A.y1<y2<y3 B.y1<y3<y2 C.y3<y2<y1 D.y2<y1<y3
11.二次函数y=3x2,y=-3x2,,的图象的共同点是 ( )
A.都关于原点对称,开口方向向下 B.都关于x轴对称,y随x的增大而增大
C.都关于y轴对称,y随x的增大而减小 D.都关于y轴对称,顶点都是原点
12.在函数①y=3x2;②;③中,图象开口按从大到小的顺序排列的是
( )
A.①>②>③ B.①>③>② C.②>③>① D.②>①>③
13.已知a≠0,在同一直角坐标系中,函数y=ax与y=ax2的图象有可能是 ( )
14.已知抛物线y=ax2经过点(1,3),当y=9时,求x的值.
15.一个二次函数,它的对称轴是y轴,顶点是原点,且经过点(-1,-4).
(1)写出这个二次函数的解析式; (2)画出这个函数的图象.
(3)在对称轴左侧部分,y随x的增大而怎样变化
16.画出二次函数y=-x2的图象.
(1)指出它的图象与x轴的交点坐标;
(2)当x取什么值时,y的值最大 最大值是多少
(3)当1<x<2时,求y的取值范围;
(4)当-3<x<2时,求y的取值范围.
17.一个函数的图象是以原点为顶点,y轴为对称轴的抛物线,且过点M(2,2).
(1)求出这个函数的关系式,并画出函数图象;
(2)写出抛物线上与点M关于y轴对称的点N的坐标,并求出△MON的面积.
18.二次函数y=ax2与直线y=2x-3交于点P(1,b).
(1)求a,b的值;
(2)写出二次函数的关系式,并指出当x取何值时,y随x的增大而减小
19.如图,已知点P是y=x2上在第一象限内的一点,点A的坐标是(3,0).
(1)设点P的坐标是(x,y),求△OPA的面积S与y的关系式;
(2)S是y的什么函数 S是x的什么函数
20.如图,已知直线过A(4,0)、B(0,4)两点,它与二次函数y=ax2的图象在第一象限内相交于点P.若△AOP的面积为,求a的值.
参考答案
1.向上 y轴 (0,0) 0 小 0 >0 <0
2.向下 y轴 (0,0) 0 大 0 <0 >0
3.-1 4.-1 5.y=-ax2 6.. 7.2
8.D 9.B 10.C 11.D 12.C 13.C
14.把(1,3)代入得a=3,则y=3x2,再把y=9代入y=3x2,得.
15.(1)设二次函数为y=ax2,把(-1,-4)代入上式,得a=-4,则y=-4x2. (2)略
(3)y随x的增大而增大.
16.图略 (1)(0.0) (2)x=0时,y最大=0 (3) -4<y<-1 (4) -9<y<0
17.(1)设y=ax2,把(-2,2)代入y=ax2,得,则,图象略.
(2)N(2,2),.
18.(1)把P(1,b)代入y=2x-3,得b=-1,则P(1,-1),再把P(1,-1)代入y=ax2,得
a=-. (2)y=-x2,当x>0时,y随x的增大而减小.
19.(1) (2)S是y的一次函数,,所以S是x的二次函数.
20.设点P(x,y),直线AB的解析式为y=kx+b,将A(4,0)和B(0,4)分别代入y=kx+b,得k=-1,b=4,则y=-x+4,又因为△AOP的面积为,所以,再把代入y=-x+4,得,所以.再把代入y=ax2,得.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
