苏教版(2019)高中数学选择性必修第一册 《3.3.1 抛物线的标准方程》学案 (含答案)
文档属性
| 名称 | 苏教版(2019)高中数学选择性必修第一册 《3.3.1 抛物线的标准方程》学案 (含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 688.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-29 00:00:00 | ||
图片预览




文档简介
§3.3.1 抛物线的标准方程
目标要求
1、理解并掌握抛物线的标准方程的推导.
2、理解并掌握抛物线标准方程的求法.
3、理解并掌握抛物线的定义及应用.
4、理解并掌握抛物线的实际应用.
学科素养目标
本章内容的处理方式与“直线与方程”“圆与方程”一样,都以渗透解析几何的基本思想为教学目标,以“展示背景,建立曲线概念;建立方程,利用方程研究曲线性质”为主线,从特殊到一般,在学生具有较多感性认识的基础上建立一般曲线方程的概念.这种从感性到理性的学习过程符合学生的认知发展规律.
本章以椭圆、双曲线、抛物线为载体,首先从生活实际和数学实验中抽象出曲线的定义,进而类比直线、圆的研究方法,建立恰当的直角坐标系,得到圆锥曲线的方程,并利用方程研究圆锥曲线的性质.在对三种曲线的研究过程中,虽然这三种曲线各有特点,但研究的思路和方法是一致的,这样可以让学生充分感受和理解解析几何研究问题的基本思路.最后通过“链接”,从圆锥曲线的统一定义的角度进一步认识三种圆锥曲线的内在关系.
重点难点
重点:抛物线的定义及应用;
难点:抛物线的实际应用.
教学过程
基础知识点
1. 抛物线的定义
文字语言:平面内到一个定点F和一条定直线l(F不在l上)的距离相等的点的轨迹叫作抛物线,定点F叫作抛物线的焦点,定直线l叫作抛物线的准线.
【课前预习思考】
定义中为什么要求直线l不经过点F
提示:当直线l经过点F时,点的轨迹是过点F且垂直于直线l的一条直线,而不是抛物线.
2.抛物线的标准方程
由于抛物线焦点位置不同,方程也就不同,故抛物线的标准方程有以下几种形式:y2=2px(p>0),y2=-2px(p>0),x2=2py(p>0),x2=-2py(p>0).
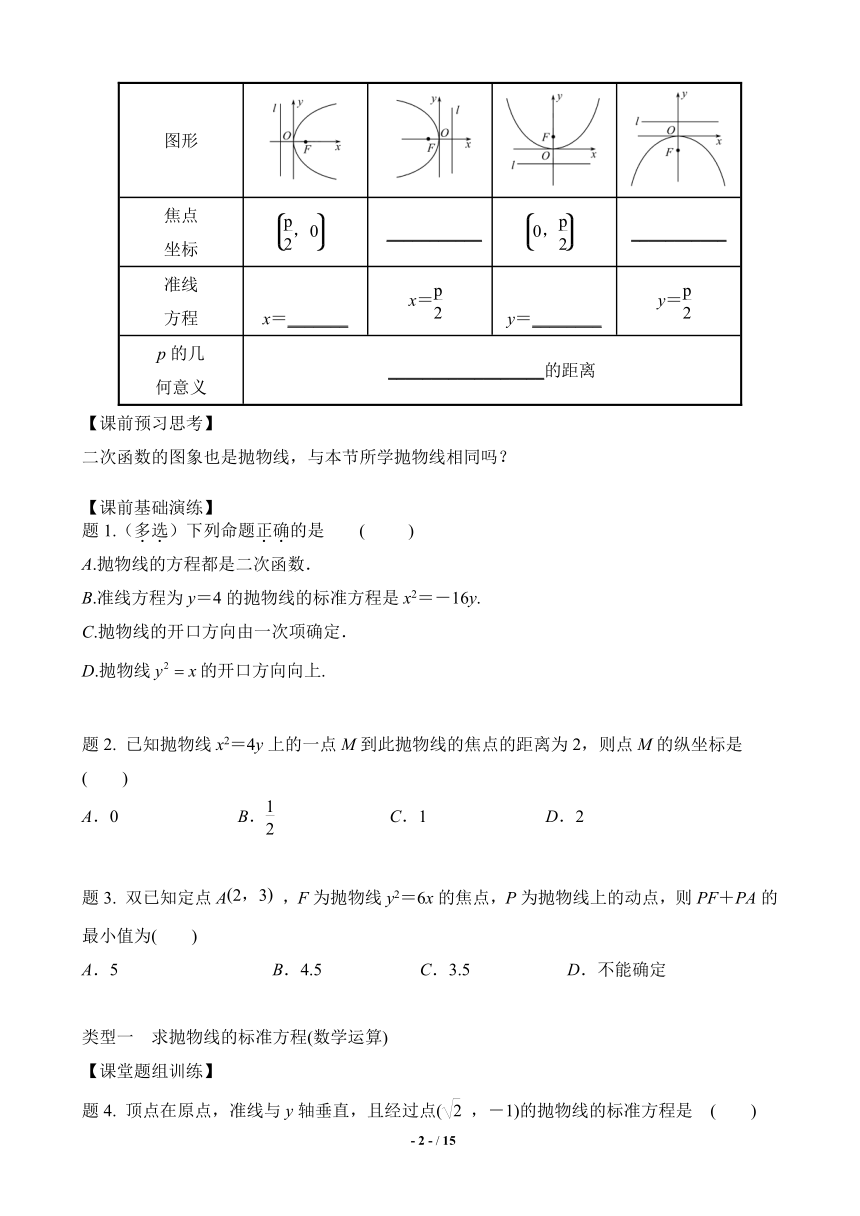
现将这四种抛物线对应的标准方程、图形、焦点坐标及准线方程列表如下:
标准方程 y2=2px(p>0) y2=-2px(p>0) x2=2py(p>0) x2=-2py(p>0)
图形
焦点坐标 ___________ ___________
准线方程 x=_______ x= y=________ y=
p的几何意义 __________________的距离
【课前预习思考】
二次函数的图象也是抛物线,与本节所学抛物线相同吗?
【课前基础演练】
题1.(多选)下列命题正确的是 ( )
A.抛物线的方程都是二次函数.
B.准线方程为y=4的抛物线的标准方程是x2=-16y.
C.抛物线的开口方向由一次项确定.
D.抛物线的开口方向向上.
题2. 已知抛物线x2=4y上的一点M到此抛物线的焦点的距离为2,则点M的纵坐标是 ( )
A.0 B. C.1 D.2
题3. 双已知定点A,F为抛物线y2=6x的焦点,P为抛物线上的动点,则PF+PA的最小值为( )
A.5 B.4.5 C.3.5 D.不能确定
类型一 求抛物线的标准方程(数学运算)
【课堂题组训练】
题4. 顶点在原点,准线与y轴垂直,且经过点(,-1)的抛物线的标准方程是 ( )
A.y2=-2x B.y2=2x C.x2=2y D.x2=-2y
题5. (多选题)设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,MF=5.若以MF为直径的圆过点(0,2),则C的方程可能为 ( )
A.y2=x B.y2=2x C.y2=4x D. y2=16x
题6. 求焦点在直线x-2y-4=0上的抛物线的标准方程.
【教师补充训练】
题7. 根据下列条件分别求抛物线的标准方程.
(1)抛物线的焦点是双曲线16x2-9y2=144的左顶点;
(2)抛物线的焦点F在x轴上,直线y=-3与抛物线交于点A,AF=5.
类型二 抛物线的定义及其应用(逻辑推理)
【典例】题8. (多选题)已知抛物线的顶点在原点,焦点在y轴上,抛物线上的点P(m,-2)到焦点的距离为4,则m的值为 ( )
A.4 B.-2 C.-4 D.2
题9. 动圆的圆心在抛物线y2=8x上,且动圆恒与直线x+2=0相切,则动圆必过定点 ( )
A.(4,0) B.(2,0) C.(0,2) D.(0,-2)
题10. 已知动圆过点(1,0),且与直线x=-1相切,则动圆的圆心的轨迹是________.
【课堂题组训练】
题11. 已知A为抛物线C:y2=2px(p>0)上一点,点A到C的焦点的距离为12,到y轴的距离为9,则p= ( )
A.2 B.3 C.6 D.9
题12. 若位于y轴右侧的动点M到F的距离比它到y轴的距离大.求点M的轨迹方程.
类型三 抛物线的实际应用(数学建模)
【典例】题13. 河上有一抛物线形拱桥,当水面距拱桥顶5 m时,水面宽为8 m,一小船宽4 m,高2 m,载货后船露出水面上的部分高0.75 m,问:水面上涨到与抛物线拱桥拱顶相距多少米时,小船开始不能通航?
【课堂跟踪训练】
题14. 如图是一种加热水和食物的太阳灶,上面装有可旋转的抛物面形的反光镜,镜的轴截面是抛物线的一部分,盛水和食物的容器放在抛物线的焦点处,容器由若干根等长的铁筋焊接在一起的架子支撑.已知镜口圆的直径为12米,镜深2米,若把盛水和食物的容器近似地看作点,求每根铁筋的长度为多少米.
【教师备选类型】 抛物线的最值问题 (数学运算)
【典例】题15. 已知抛物线y2=4x的焦点是F,点P是抛物线上的动点,对于定点A(4,2),求PA+PF的最小值,并求出取最小值时的P点坐标.
【课堂题组训练】
题16. 已知点P是抛物线y2=2x上的一个动点,则点P到点A(0,2)的距离与点P到该抛物线准线的距离之和的最小值为 ( )
A. B.3 C. D.
【课后巩固习题】
题17. 对抛物线x2=4y,下列描述正确的是 ( )
A.开口向上,焦点为(0,1) B.开口向上,焦点为
C.开口向右,焦点为(1,0) D.开口向右,焦点为
题18. 已知抛物线y2=2px(p>0)的焦点为F,点P1(x1,y1),P2(x2,y2),P3(x3,y3)在抛物线上,且2x2=x1+x3,则有 ( )
A.FP1+FP2=FP3 B.FP+FP=FP C.2FP2=FP1+FP3 D.FP=FP1·FP3
题19. 若抛物线y2=x的焦点与椭圆+=1的左焦点重合,则m的值为 ( )
A.- B. C.-2 D.2
题20. 抛物线y2=4mx(m>0)的焦点到双曲线-=1的一条渐近线的距离为3,则此抛物线的方程为________.
题21. 如图所示,等边三角形OAB的边长为8,且其三个顶点均在抛物线E:x2=2py(p>0)上.求抛物线E的方程.
§3.3.1 抛物线的标准方程答案
目标要求
1、理解并掌握抛物线的标准方程的推导.
2、理解并掌握抛物线标准方程的求法.
3、理解并掌握抛物线的定义及应用.
4、理解并掌握抛物线的实际应用.
学科素养目标
本章内容的处理方式与“直线与方程”“圆与方程”一样,都以渗透解析几何的基本思想为教学目标,以“展示背景,建立曲线概念;建立方程,利用方程研究曲线性质”为主线,从特殊到一般,在学生具有较多感性认识的基础上建立一般曲线方程的概念.这种从感性到理性的学习过程符合学生的认知发展规律.
本章以椭圆、双曲线、抛物线为载体,首先从生活实际和数学实验中抽象出曲线的定义,进而类比直线、圆的研究方法,建立恰当的直角坐标系,得到圆锥曲线的方程,并利用方程研究圆锥曲线的性质.在对三种曲线的研究过程中,虽然这三种曲线各有特点,但研究的思路和方法是一致的,这样可以让学生充分感受和理解解析几何研究问题的基本思路.最后通过“链接”,从圆锥曲线的统一定义的角度进一步认识三种圆锥曲线的内在关系.
重点难点
重点:抛物线的定义及应用;
难点:抛物线的实际应用.
教学过程
基础知识点
1. 抛物线的定义
文字语言:平面内到一个定点F和一条定直线l(F不在l上)的距离相等的点的轨迹叫作抛物线,定点F叫作抛物线的焦点,定直线l叫作抛物线的准线.
【课前预习思考】
定义中为什么要求直线l不经过点F
提示:当直线l经过点F时,点的轨迹是过点F且垂直于直线l的一条直线,而不是抛物线.
2.抛物线的标准方程
由于抛物线焦点位置不同,方程也就不同,故抛物线的标准方程有以下几种形式:y2=2px(p>0),y2=-2px(p>0),x2=2py(p>0),x2=-2py(p>0).
现将这四种抛物线对应的标准方程、图形、焦点坐标及准线方程列表如下:
标准方程 y2=2px(p>0) y2=-2px(p>0) x2=2py(p>0) x2=-2py(p>0)
图形
焦点坐标
准线方程 x=- x= y=- y=
p的几何意义 焦点到准线的距离
【课前预习思考】
二次函数的图象也是抛物线,与本节所学抛物线相同吗?
提示:不完全相同.当抛物线的开口向上或向下时可以看作是二次函数的图象,当开口向左或向右时不能看作二次函数的图象.
【课前基础演练】
题1.(多选)下列命题正确的是 ( )
A.抛物线的方程都是二次函数.
B.准线方程为y=4的抛物线的标准方程是x2=-16y.
C.抛物线的开口方向由一次项确定.
D.抛物线的开口方向向上.
【答案】BC
【解析】A×.当抛物线是开口向上或向下时,该曲线也是二次函数的图象;当抛物线是开口向右或向左时,该曲线不是二次函数的图象.
B√.由题意可设抛物线方程为x2=-2py(p>0),因为抛物线的准线方程为y==4,所以p=8,
所以该抛物线的标准方程为x2=-16y.
C√.一次项决定焦点所在的坐标轴,一次项系数的正负决定焦点是在正半轴或负半轴上,故该说法正确.
D×.抛物线的开口方向向右.
故选BC.
题2. 已知抛物线x2=4y上的一点M到此抛物线的焦点的距离为2,则点M的纵坐标是 ( )
A.0 B. C.1 D.2
【解析】选C.根据抛物线方程可求得焦点坐标为(0,1),准线方程为y=-1,根据抛物线定义,得yM+1=2,解得yM=1.
题3. 双已知定点A,F为抛物线y2=6x的焦点,P为抛物线上的动点,则PF+PA的最小值为( )
A.5 B.4.5 C.3.5 D.不能确定
【解析】选C.如图所示,过点P作PM⊥准线l,垂足为M,
则PF=PM当且仅当A,P,M三点共线时,PF+PA取得最小值AM=2+=3.5.
类型一 求抛物线的标准方程(数学运算)
【课堂题组训练】
题4. 顶点在原点,准线与y轴垂直,且经过点(,-1)的抛物线的标准方程是 ( )
A.y2=-2x B.y2=2x C.x2=2y D.x2=-2y
【解析】选D.因为抛物线顶点在原点,准线与y轴垂直,且经过点(,-1),所以设抛物线的标准方程为x2=-2py,p>0,把点(,-1)代入,得2=2p,解得p=1,
所以抛物线方程为x2=-2y.
题5. (多选题)设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,MF=5.若以MF为直径的圆过点(0,2),则C的方程可能为 ( )
A.y2=x B.y2=2x C.y2=4x D. y2=16x
【解析】选CD.易知抛物线的焦点为F.由抛物线的定义,得M.设N点坐标为(0,2).因为圆过点N(0,2),所以NF⊥NM,即×=-1.①
设=t,则①式可化为t2-4t+8=0,
解得t=2,即p2-10p+16=0,解得p=2或p=8.
题6. 求焦点在直线x-2y-4=0上的抛物线的标准方程.
【解析】当焦点在y轴上时,已知方程x-2y-4=0,
令x=0,得y=-2,所以所求抛物线的焦点为(0,-2),设抛物线的标准方程为x2=-2py(p>0),
由-=-2,得2p=8,所以所求抛物线的标准方程为x2=-8y;
当焦点在x轴上时,已知x-2y-4=0,令y=0,得x=4,所以抛物线的焦点为(4,0),
设抛物线的标准方程为y2=2px(p>0),由=4,得2p=16,所以所求抛物线的标准方程为y2=16x.
综上,所求抛物线的标准方程为x2=-8y或y2=16x.
【解题策略提醒】
抛物线标准方程的求法
(1)定义法:建立适当坐标系,利用抛物线的定义列出动点满足的条件,列出方程,进行化简,根据定义求出p,最后写出标准方程.
(2)待定系数法:由于标准方程有四种形式,因而在求方程时应首先确定焦点在哪一个半轴上,进而确定方程的形式,然后再利用已知条件确定p的值.
【教师补充训练】
题7. 根据下列条件分别求抛物线的标准方程.
(1)抛物线的焦点是双曲线16x2-9y2=144的左顶点;
(2)抛物线的焦点F在x轴上,直线y=-3与抛物线交于点A,AF=5.
【解析】(1)双曲线方程可化为-=1,左顶点为(-3,0),
由题意设抛物线方程为y2=-2px(p>0)且-=-3,所以p=6,所以抛物线的方程为y2=-12x.
(2)设所求焦点在x轴上的抛物线的方程为y2=2px(p≠0),A(m,-3),
由抛物线定义,得5=AF=.又(-3)2=2pm,所以p=±1或p=±9,
故所求抛物线方程为y2=±2x或y2=±18x.
类型二 抛物线的定义及其应用(逻辑推理)
【典例】题8. (多选题)已知抛物线的顶点在原点,焦点在y轴上,抛物线上的点P(m,-2)到焦点的距离为4,则m的值为 ( )
A.4 B.-2 C.-4 D.2
【解析】选AC.由题可设抛物线的标准方程为x2=
-2py(p>0),由定义知点P到准线的距离为4,故+2=4,所以p=4,所以x2=-8y.将点P的坐标代入x2=-8y,得m=±4.
题9. 动圆的圆心在抛物线y2=8x上,且动圆恒与直线x+2=0相切,则动圆必过定点 ( )
A.(4,0) B.(2,0) C.(0,2) D.(0,-2)
【解析】选B.因为圆心到直线x+2=0的距离等于到抛物线焦点的距离,所以定点为(2,0).
题10. 已知动圆过点(1,0),且与直线x=-1相切,则动圆的圆心的轨迹是________.
【解析】设动圆的圆心坐标为(x,y),则圆心到点(1,0)的距离与其到直线x=-1的距离相等,根据抛物线的定义易知动圆的圆心的轨迹是抛物线.
答案:抛物线
【解题策略提醒】
抛物线的判断方法
(1)定义判断:可以看动点是否符合抛物线的定义,即到定点的距离等于到定直线(直线不过定点)的距离.
(2)方程判断:求出动点的轨迹方程,看方程是否符合抛物线的方程.
【课堂题组训练】
题11. 已知A为抛物线C:y2=2px(p>0)上一点,点A到C的焦点的距离为12,到y轴的距离为9,则p= ( )
A.2 B.3 C.6 D.9
【解析】选C.设抛物线的焦点为F,由抛物线的定义知|AF|=xA+=12,即12=9+,解得p=6.
题12. 若位于y轴右侧的动点M到F的距离比它到y轴的距离大.求点M的轨迹方程.
【解析】由于位于y轴右侧的动点M到F的距离比它到y轴的距离大,所以动点M到F的距离与它到直线l:x=-的距离相等.由抛物线的定义知动点M的轨迹是以F为焦点,l为准线的抛物线(不包含原点),其方程应为y2=2px(p>0)的形式,而=,所以p=1,2p=2,故点M的轨迹方程为y2=2x(x≠0).
类型三 抛物线的实际应用(数学建模)
【典例】题13. 河上有一抛物线形拱桥,当水面距拱桥顶5 m时,水面宽为8 m,一小船宽4 m,高2 m,载货后船露出水面上的部分高0.75 m,问:水面上涨到与抛物线拱桥拱顶相距多少米时,小船开始不能通航?
【思路导引】
以桥的顶点为原点,拱高所在直线为y轴建立直角坐标系后,利用已知条件求出抛物线方程,然后求解.
【解析】以拱桥的拱顶为原点,以过拱顶且平行于水面的直线为x轴,建立平面直角坐标系(图略).设抛物线方程为x2=-2py(p>0),由题意可知,点B(4,
-5)在抛物线上,故p=,得x2=-y.当船面两侧和抛物线接触时,船不能通航,设此时船面宽为AA′,则A(2,yA),由22=-yA,得yA=-.又知船面露出水面上的部分高为0.75 m,
所以h=|yA|+0.75=2(m).所以水面上涨到与抛物线形拱桥拱顶相距2 m时,小船开始不能通航.
【解题策略提醒】
求抛物线实际应用问题的基本步骤
(1)建立适当的坐标系.
(2)设出合适的抛物线标准方程.
(3)通过计算求出抛物线的标准方程.
(4)求出需要求出的量.
(5)还原到实际问题中,从而解决实际问题.
【课堂跟踪训练】
题14. 如图是一种加热水和食物的太阳灶,上面装有可旋转的抛物面形的反光镜,镜的轴截面是抛物线的一部分,盛水和食物的容器放在抛物线的焦点处,容器由若干根等长的铁筋焊接在一起的架子支撑.已知镜口圆的直径为12米,镜深2米,若把盛水和食物的容器近似地看作点,求每根铁筋的长度为多少米.
【解析】如图,在反光镜的轴截面内建立直角坐标系,使反光镜的顶点(即抛物线的顶点)与原点重合,x轴垂直于镜口直径.
由已知,得A点坐标是(2,6),设抛物线方程为y2=2px(p>0),则36=2p×2,p=9.
所以所求抛物线的标准方程是y2=18x,
焦点坐标是F.因为盛水和食物的容器在焦点处,所以A,F两点间的距离即为每根铁筋长.
AF==6.5,故每根铁筋的长度是6.5米.
【教师备选类型】 抛物线的最值问题 (数学运算)
【典例】题15. 已知抛物线y2=4x的焦点是F,点P是抛物线上的动点,对于定点A(4,2),求PA+PF的最小值,并求出取最小值时的P点坐标.
【思路导引】利用抛物线的定义,把|PF|转化为到准线的距离.
【解析】如图,作PN⊥l于N(l为准线),作AB⊥l于B,则PA+PF=PA+PN≥AB,
当且仅当P为AB与抛物线的交点时,取等号.所以(PA+PF)min=AB=4+1=5.
此时yP=2,代入抛物线得xP=1,所以P(1,2).
【解题策略提醒】
在抛物线中求解与焦点有关的两点间距离和的最小值时,往往用抛物线的定义进行转化,即化折线为直线解决最值问题.
【课堂题组训练】
题16. 已知点P是抛物线y2=2x上的一个动点,则点P到点A(0,2)的距离与点P到该抛物线准线的距离之和的最小值为 ( )
A. B.3 C. D.
【解析】选A.由抛物线的定义可知,抛物线上的点到准线的距离等于到焦点的距离.如图所示,
所以点P到准线x=-的距离d=PF,易知点A(0,2)在抛物线y2=2x的外部,
连接AF,交y2=2x于点P′,欲使所求距离之和最小,只需A,P′,F共线,
所以其最小值为AF==.
【课后巩固习题】
题17. 对抛物线x2=4y,下列描述正确的是 ( )
A.开口向上,焦点为(0,1) B.开口向上,焦点为
C.开口向右,焦点为(1,0) D.开口向右,焦点为
【解析】选A.抛物线x2=4y开口向上,焦点为(0,1).
题18. 已知抛物线y2=2px(p>0)的焦点为F,点P1(x1,y1),P2(x2,y2),P3(x3,y3)在抛物线上,且2x2=x1+x3,则有 ( )
A.FP1+FP2=FP3 B.FP+FP=FP C.2FP2=FP1+FP3 D.FP=FP1·FP3
【解析】选C.如图所示,由定义知FP1=x1+,FP2=x2+,FP3=x3+,
由2x2=x1+x3知,2FP2=FP1+FP3.
题19. 若抛物线y2=x的焦点与椭圆+=1的左焦点重合,则m的值为 ( )
A.- B. C.-2 D.2
【解析】选A.抛物线y2=x的焦点坐标为,椭圆+=1,因为a2=7,b2=3,
所以c2=a2-b2=4,所以椭圆的左焦点坐标为(-2,0),
因为抛物线y2=x的焦点与椭圆+=1的左焦点重合,所以=-2,所以m=-.
题20. 抛物线y2=4mx(m>0)的焦点到双曲线-=1的一条渐近线的距离为3,则此抛物线的方程为________.
【解析】抛物线y2=4mx(m>0)的焦点为F(m,0),双曲线-=1的渐近线方程为3x±4y=0,则F(m,0)到渐近线的距离为==3 m=5,所以抛物线的方程为y2=20x.
答案:y2=20x
题21. 如图所示,等边三角形OAB的边长为8,且其三个顶点均在抛物线E:x2=2py(p>0)上.求抛物线E的方程.
【解析】依题意,OB=8,∠BOy=30°.设B(x,y),则x=OBsin 30°=4,y=OBcos 30°=12.
因为点B(4,12)在x2=2py上,所以(4)2=2p×12,解得p=2.故抛物线E的方程为x2=4y.
- 6 - / 14
目标要求
1、理解并掌握抛物线的标准方程的推导.
2、理解并掌握抛物线标准方程的求法.
3、理解并掌握抛物线的定义及应用.
4、理解并掌握抛物线的实际应用.
学科素养目标
本章内容的处理方式与“直线与方程”“圆与方程”一样,都以渗透解析几何的基本思想为教学目标,以“展示背景,建立曲线概念;建立方程,利用方程研究曲线性质”为主线,从特殊到一般,在学生具有较多感性认识的基础上建立一般曲线方程的概念.这种从感性到理性的学习过程符合学生的认知发展规律.
本章以椭圆、双曲线、抛物线为载体,首先从生活实际和数学实验中抽象出曲线的定义,进而类比直线、圆的研究方法,建立恰当的直角坐标系,得到圆锥曲线的方程,并利用方程研究圆锥曲线的性质.在对三种曲线的研究过程中,虽然这三种曲线各有特点,但研究的思路和方法是一致的,这样可以让学生充分感受和理解解析几何研究问题的基本思路.最后通过“链接”,从圆锥曲线的统一定义的角度进一步认识三种圆锥曲线的内在关系.
重点难点
重点:抛物线的定义及应用;
难点:抛物线的实际应用.
教学过程
基础知识点
1. 抛物线的定义
文字语言:平面内到一个定点F和一条定直线l(F不在l上)的距离相等的点的轨迹叫作抛物线,定点F叫作抛物线的焦点,定直线l叫作抛物线的准线.
【课前预习思考】
定义中为什么要求直线l不经过点F
提示:当直线l经过点F时,点的轨迹是过点F且垂直于直线l的一条直线,而不是抛物线.
2.抛物线的标准方程
由于抛物线焦点位置不同,方程也就不同,故抛物线的标准方程有以下几种形式:y2=2px(p>0),y2=-2px(p>0),x2=2py(p>0),x2=-2py(p>0).
现将这四种抛物线对应的标准方程、图形、焦点坐标及准线方程列表如下:
标准方程 y2=2px(p>0) y2=-2px(p>0) x2=2py(p>0) x2=-2py(p>0)
图形
焦点坐标 ___________ ___________
准线方程 x=_______ x= y=________ y=
p的几何意义 __________________的距离
【课前预习思考】
二次函数的图象也是抛物线,与本节所学抛物线相同吗?
【课前基础演练】
题1.(多选)下列命题正确的是 ( )
A.抛物线的方程都是二次函数.
B.准线方程为y=4的抛物线的标准方程是x2=-16y.
C.抛物线的开口方向由一次项确定.
D.抛物线的开口方向向上.
题2. 已知抛物线x2=4y上的一点M到此抛物线的焦点的距离为2,则点M的纵坐标是 ( )
A.0 B. C.1 D.2
题3. 双已知定点A,F为抛物线y2=6x的焦点,P为抛物线上的动点,则PF+PA的最小值为( )
A.5 B.4.5 C.3.5 D.不能确定
类型一 求抛物线的标准方程(数学运算)
【课堂题组训练】
题4. 顶点在原点,准线与y轴垂直,且经过点(,-1)的抛物线的标准方程是 ( )
A.y2=-2x B.y2=2x C.x2=2y D.x2=-2y
题5. (多选题)设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,MF=5.若以MF为直径的圆过点(0,2),则C的方程可能为 ( )
A.y2=x B.y2=2x C.y2=4x D. y2=16x
题6. 求焦点在直线x-2y-4=0上的抛物线的标准方程.
【教师补充训练】
题7. 根据下列条件分别求抛物线的标准方程.
(1)抛物线的焦点是双曲线16x2-9y2=144的左顶点;
(2)抛物线的焦点F在x轴上,直线y=-3与抛物线交于点A,AF=5.
类型二 抛物线的定义及其应用(逻辑推理)
【典例】题8. (多选题)已知抛物线的顶点在原点,焦点在y轴上,抛物线上的点P(m,-2)到焦点的距离为4,则m的值为 ( )
A.4 B.-2 C.-4 D.2
题9. 动圆的圆心在抛物线y2=8x上,且动圆恒与直线x+2=0相切,则动圆必过定点 ( )
A.(4,0) B.(2,0) C.(0,2) D.(0,-2)
题10. 已知动圆过点(1,0),且与直线x=-1相切,则动圆的圆心的轨迹是________.
【课堂题组训练】
题11. 已知A为抛物线C:y2=2px(p>0)上一点,点A到C的焦点的距离为12,到y轴的距离为9,则p= ( )
A.2 B.3 C.6 D.9
题12. 若位于y轴右侧的动点M到F的距离比它到y轴的距离大.求点M的轨迹方程.
类型三 抛物线的实际应用(数学建模)
【典例】题13. 河上有一抛物线形拱桥,当水面距拱桥顶5 m时,水面宽为8 m,一小船宽4 m,高2 m,载货后船露出水面上的部分高0.75 m,问:水面上涨到与抛物线拱桥拱顶相距多少米时,小船开始不能通航?
【课堂跟踪训练】
题14. 如图是一种加热水和食物的太阳灶,上面装有可旋转的抛物面形的反光镜,镜的轴截面是抛物线的一部分,盛水和食物的容器放在抛物线的焦点处,容器由若干根等长的铁筋焊接在一起的架子支撑.已知镜口圆的直径为12米,镜深2米,若把盛水和食物的容器近似地看作点,求每根铁筋的长度为多少米.
【教师备选类型】 抛物线的最值问题 (数学运算)
【典例】题15. 已知抛物线y2=4x的焦点是F,点P是抛物线上的动点,对于定点A(4,2),求PA+PF的最小值,并求出取最小值时的P点坐标.
【课堂题组训练】
题16. 已知点P是抛物线y2=2x上的一个动点,则点P到点A(0,2)的距离与点P到该抛物线准线的距离之和的最小值为 ( )
A. B.3 C. D.
【课后巩固习题】
题17. 对抛物线x2=4y,下列描述正确的是 ( )
A.开口向上,焦点为(0,1) B.开口向上,焦点为
C.开口向右,焦点为(1,0) D.开口向右,焦点为
题18. 已知抛物线y2=2px(p>0)的焦点为F,点P1(x1,y1),P2(x2,y2),P3(x3,y3)在抛物线上,且2x2=x1+x3,则有 ( )
A.FP1+FP2=FP3 B.FP+FP=FP C.2FP2=FP1+FP3 D.FP=FP1·FP3
题19. 若抛物线y2=x的焦点与椭圆+=1的左焦点重合,则m的值为 ( )
A.- B. C.-2 D.2
题20. 抛物线y2=4mx(m>0)的焦点到双曲线-=1的一条渐近线的距离为3,则此抛物线的方程为________.
题21. 如图所示,等边三角形OAB的边长为8,且其三个顶点均在抛物线E:x2=2py(p>0)上.求抛物线E的方程.
§3.3.1 抛物线的标准方程答案
目标要求
1、理解并掌握抛物线的标准方程的推导.
2、理解并掌握抛物线标准方程的求法.
3、理解并掌握抛物线的定义及应用.
4、理解并掌握抛物线的实际应用.
学科素养目标
本章内容的处理方式与“直线与方程”“圆与方程”一样,都以渗透解析几何的基本思想为教学目标,以“展示背景,建立曲线概念;建立方程,利用方程研究曲线性质”为主线,从特殊到一般,在学生具有较多感性认识的基础上建立一般曲线方程的概念.这种从感性到理性的学习过程符合学生的认知发展规律.
本章以椭圆、双曲线、抛物线为载体,首先从生活实际和数学实验中抽象出曲线的定义,进而类比直线、圆的研究方法,建立恰当的直角坐标系,得到圆锥曲线的方程,并利用方程研究圆锥曲线的性质.在对三种曲线的研究过程中,虽然这三种曲线各有特点,但研究的思路和方法是一致的,这样可以让学生充分感受和理解解析几何研究问题的基本思路.最后通过“链接”,从圆锥曲线的统一定义的角度进一步认识三种圆锥曲线的内在关系.
重点难点
重点:抛物线的定义及应用;
难点:抛物线的实际应用.
教学过程
基础知识点
1. 抛物线的定义
文字语言:平面内到一个定点F和一条定直线l(F不在l上)的距离相等的点的轨迹叫作抛物线,定点F叫作抛物线的焦点,定直线l叫作抛物线的准线.
【课前预习思考】
定义中为什么要求直线l不经过点F
提示:当直线l经过点F时,点的轨迹是过点F且垂直于直线l的一条直线,而不是抛物线.
2.抛物线的标准方程
由于抛物线焦点位置不同,方程也就不同,故抛物线的标准方程有以下几种形式:y2=2px(p>0),y2=-2px(p>0),x2=2py(p>0),x2=-2py(p>0).
现将这四种抛物线对应的标准方程、图形、焦点坐标及准线方程列表如下:
标准方程 y2=2px(p>0) y2=-2px(p>0) x2=2py(p>0) x2=-2py(p>0)
图形
焦点坐标
准线方程 x=- x= y=- y=
p的几何意义 焦点到准线的距离
【课前预习思考】
二次函数的图象也是抛物线,与本节所学抛物线相同吗?
提示:不完全相同.当抛物线的开口向上或向下时可以看作是二次函数的图象,当开口向左或向右时不能看作二次函数的图象.
【课前基础演练】
题1.(多选)下列命题正确的是 ( )
A.抛物线的方程都是二次函数.
B.准线方程为y=4的抛物线的标准方程是x2=-16y.
C.抛物线的开口方向由一次项确定.
D.抛物线的开口方向向上.
【答案】BC
【解析】A×.当抛物线是开口向上或向下时,该曲线也是二次函数的图象;当抛物线是开口向右或向左时,该曲线不是二次函数的图象.
B√.由题意可设抛物线方程为x2=-2py(p>0),因为抛物线的准线方程为y==4,所以p=8,
所以该抛物线的标准方程为x2=-16y.
C√.一次项决定焦点所在的坐标轴,一次项系数的正负决定焦点是在正半轴或负半轴上,故该说法正确.
D×.抛物线的开口方向向右.
故选BC.
题2. 已知抛物线x2=4y上的一点M到此抛物线的焦点的距离为2,则点M的纵坐标是 ( )
A.0 B. C.1 D.2
【解析】选C.根据抛物线方程可求得焦点坐标为(0,1),准线方程为y=-1,根据抛物线定义,得yM+1=2,解得yM=1.
题3. 双已知定点A,F为抛物线y2=6x的焦点,P为抛物线上的动点,则PF+PA的最小值为( )
A.5 B.4.5 C.3.5 D.不能确定
【解析】选C.如图所示,过点P作PM⊥准线l,垂足为M,
则PF=PM当且仅当A,P,M三点共线时,PF+PA取得最小值AM=2+=3.5.
类型一 求抛物线的标准方程(数学运算)
【课堂题组训练】
题4. 顶点在原点,准线与y轴垂直,且经过点(,-1)的抛物线的标准方程是 ( )
A.y2=-2x B.y2=2x C.x2=2y D.x2=-2y
【解析】选D.因为抛物线顶点在原点,准线与y轴垂直,且经过点(,-1),所以设抛物线的标准方程为x2=-2py,p>0,把点(,-1)代入,得2=2p,解得p=1,
所以抛物线方程为x2=-2y.
题5. (多选题)设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,MF=5.若以MF为直径的圆过点(0,2),则C的方程可能为 ( )
A.y2=x B.y2=2x C.y2=4x D. y2=16x
【解析】选CD.易知抛物线的焦点为F.由抛物线的定义,得M.设N点坐标为(0,2).因为圆过点N(0,2),所以NF⊥NM,即×=-1.①
设=t,则①式可化为t2-4t+8=0,
解得t=2,即p2-10p+16=0,解得p=2或p=8.
题6. 求焦点在直线x-2y-4=0上的抛物线的标准方程.
【解析】当焦点在y轴上时,已知方程x-2y-4=0,
令x=0,得y=-2,所以所求抛物线的焦点为(0,-2),设抛物线的标准方程为x2=-2py(p>0),
由-=-2,得2p=8,所以所求抛物线的标准方程为x2=-8y;
当焦点在x轴上时,已知x-2y-4=0,令y=0,得x=4,所以抛物线的焦点为(4,0),
设抛物线的标准方程为y2=2px(p>0),由=4,得2p=16,所以所求抛物线的标准方程为y2=16x.
综上,所求抛物线的标准方程为x2=-8y或y2=16x.
【解题策略提醒】
抛物线标准方程的求法
(1)定义法:建立适当坐标系,利用抛物线的定义列出动点满足的条件,列出方程,进行化简,根据定义求出p,最后写出标准方程.
(2)待定系数法:由于标准方程有四种形式,因而在求方程时应首先确定焦点在哪一个半轴上,进而确定方程的形式,然后再利用已知条件确定p的值.
【教师补充训练】
题7. 根据下列条件分别求抛物线的标准方程.
(1)抛物线的焦点是双曲线16x2-9y2=144的左顶点;
(2)抛物线的焦点F在x轴上,直线y=-3与抛物线交于点A,AF=5.
【解析】(1)双曲线方程可化为-=1,左顶点为(-3,0),
由题意设抛物线方程为y2=-2px(p>0)且-=-3,所以p=6,所以抛物线的方程为y2=-12x.
(2)设所求焦点在x轴上的抛物线的方程为y2=2px(p≠0),A(m,-3),
由抛物线定义,得5=AF=.又(-3)2=2pm,所以p=±1或p=±9,
故所求抛物线方程为y2=±2x或y2=±18x.
类型二 抛物线的定义及其应用(逻辑推理)
【典例】题8. (多选题)已知抛物线的顶点在原点,焦点在y轴上,抛物线上的点P(m,-2)到焦点的距离为4,则m的值为 ( )
A.4 B.-2 C.-4 D.2
【解析】选AC.由题可设抛物线的标准方程为x2=
-2py(p>0),由定义知点P到准线的距离为4,故+2=4,所以p=4,所以x2=-8y.将点P的坐标代入x2=-8y,得m=±4.
题9. 动圆的圆心在抛物线y2=8x上,且动圆恒与直线x+2=0相切,则动圆必过定点 ( )
A.(4,0) B.(2,0) C.(0,2) D.(0,-2)
【解析】选B.因为圆心到直线x+2=0的距离等于到抛物线焦点的距离,所以定点为(2,0).
题10. 已知动圆过点(1,0),且与直线x=-1相切,则动圆的圆心的轨迹是________.
【解析】设动圆的圆心坐标为(x,y),则圆心到点(1,0)的距离与其到直线x=-1的距离相等,根据抛物线的定义易知动圆的圆心的轨迹是抛物线.
答案:抛物线
【解题策略提醒】
抛物线的判断方法
(1)定义判断:可以看动点是否符合抛物线的定义,即到定点的距离等于到定直线(直线不过定点)的距离.
(2)方程判断:求出动点的轨迹方程,看方程是否符合抛物线的方程.
【课堂题组训练】
题11. 已知A为抛物线C:y2=2px(p>0)上一点,点A到C的焦点的距离为12,到y轴的距离为9,则p= ( )
A.2 B.3 C.6 D.9
【解析】选C.设抛物线的焦点为F,由抛物线的定义知|AF|=xA+=12,即12=9+,解得p=6.
题12. 若位于y轴右侧的动点M到F的距离比它到y轴的距离大.求点M的轨迹方程.
【解析】由于位于y轴右侧的动点M到F的距离比它到y轴的距离大,所以动点M到F的距离与它到直线l:x=-的距离相等.由抛物线的定义知动点M的轨迹是以F为焦点,l为准线的抛物线(不包含原点),其方程应为y2=2px(p>0)的形式,而=,所以p=1,2p=2,故点M的轨迹方程为y2=2x(x≠0).
类型三 抛物线的实际应用(数学建模)
【典例】题13. 河上有一抛物线形拱桥,当水面距拱桥顶5 m时,水面宽为8 m,一小船宽4 m,高2 m,载货后船露出水面上的部分高0.75 m,问:水面上涨到与抛物线拱桥拱顶相距多少米时,小船开始不能通航?
【思路导引】
以桥的顶点为原点,拱高所在直线为y轴建立直角坐标系后,利用已知条件求出抛物线方程,然后求解.
【解析】以拱桥的拱顶为原点,以过拱顶且平行于水面的直线为x轴,建立平面直角坐标系(图略).设抛物线方程为x2=-2py(p>0),由题意可知,点B(4,
-5)在抛物线上,故p=,得x2=-y.当船面两侧和抛物线接触时,船不能通航,设此时船面宽为AA′,则A(2,yA),由22=-yA,得yA=-.又知船面露出水面上的部分高为0.75 m,
所以h=|yA|+0.75=2(m).所以水面上涨到与抛物线形拱桥拱顶相距2 m时,小船开始不能通航.
【解题策略提醒】
求抛物线实际应用问题的基本步骤
(1)建立适当的坐标系.
(2)设出合适的抛物线标准方程.
(3)通过计算求出抛物线的标准方程.
(4)求出需要求出的量.
(5)还原到实际问题中,从而解决实际问题.
【课堂跟踪训练】
题14. 如图是一种加热水和食物的太阳灶,上面装有可旋转的抛物面形的反光镜,镜的轴截面是抛物线的一部分,盛水和食物的容器放在抛物线的焦点处,容器由若干根等长的铁筋焊接在一起的架子支撑.已知镜口圆的直径为12米,镜深2米,若把盛水和食物的容器近似地看作点,求每根铁筋的长度为多少米.
【解析】如图,在反光镜的轴截面内建立直角坐标系,使反光镜的顶点(即抛物线的顶点)与原点重合,x轴垂直于镜口直径.
由已知,得A点坐标是(2,6),设抛物线方程为y2=2px(p>0),则36=2p×2,p=9.
所以所求抛物线的标准方程是y2=18x,
焦点坐标是F.因为盛水和食物的容器在焦点处,所以A,F两点间的距离即为每根铁筋长.
AF==6.5,故每根铁筋的长度是6.5米.
【教师备选类型】 抛物线的最值问题 (数学运算)
【典例】题15. 已知抛物线y2=4x的焦点是F,点P是抛物线上的动点,对于定点A(4,2),求PA+PF的最小值,并求出取最小值时的P点坐标.
【思路导引】利用抛物线的定义,把|PF|转化为到准线的距离.
【解析】如图,作PN⊥l于N(l为准线),作AB⊥l于B,则PA+PF=PA+PN≥AB,
当且仅当P为AB与抛物线的交点时,取等号.所以(PA+PF)min=AB=4+1=5.
此时yP=2,代入抛物线得xP=1,所以P(1,2).
【解题策略提醒】
在抛物线中求解与焦点有关的两点间距离和的最小值时,往往用抛物线的定义进行转化,即化折线为直线解决最值问题.
【课堂题组训练】
题16. 已知点P是抛物线y2=2x上的一个动点,则点P到点A(0,2)的距离与点P到该抛物线准线的距离之和的最小值为 ( )
A. B.3 C. D.
【解析】选A.由抛物线的定义可知,抛物线上的点到准线的距离等于到焦点的距离.如图所示,
所以点P到准线x=-的距离d=PF,易知点A(0,2)在抛物线y2=2x的外部,
连接AF,交y2=2x于点P′,欲使所求距离之和最小,只需A,P′,F共线,
所以其最小值为AF==.
【课后巩固习题】
题17. 对抛物线x2=4y,下列描述正确的是 ( )
A.开口向上,焦点为(0,1) B.开口向上,焦点为
C.开口向右,焦点为(1,0) D.开口向右,焦点为
【解析】选A.抛物线x2=4y开口向上,焦点为(0,1).
题18. 已知抛物线y2=2px(p>0)的焦点为F,点P1(x1,y1),P2(x2,y2),P3(x3,y3)在抛物线上,且2x2=x1+x3,则有 ( )
A.FP1+FP2=FP3 B.FP+FP=FP C.2FP2=FP1+FP3 D.FP=FP1·FP3
【解析】选C.如图所示,由定义知FP1=x1+,FP2=x2+,FP3=x3+,
由2x2=x1+x3知,2FP2=FP1+FP3.
题19. 若抛物线y2=x的焦点与椭圆+=1的左焦点重合,则m的值为 ( )
A.- B. C.-2 D.2
【解析】选A.抛物线y2=x的焦点坐标为,椭圆+=1,因为a2=7,b2=3,
所以c2=a2-b2=4,所以椭圆的左焦点坐标为(-2,0),
因为抛物线y2=x的焦点与椭圆+=1的左焦点重合,所以=-2,所以m=-.
题20. 抛物线y2=4mx(m>0)的焦点到双曲线-=1的一条渐近线的距离为3,则此抛物线的方程为________.
【解析】抛物线y2=4mx(m>0)的焦点为F(m,0),双曲线-=1的渐近线方程为3x±4y=0,则F(m,0)到渐近线的距离为==3 m=5,所以抛物线的方程为y2=20x.
答案:y2=20x
题21. 如图所示,等边三角形OAB的边长为8,且其三个顶点均在抛物线E:x2=2py(p>0)上.求抛物线E的方程.
【解析】依题意,OB=8,∠BOy=30°.设B(x,y),则x=OBsin 30°=4,y=OBcos 30°=12.
因为点B(4,12)在x2=2py上,所以(4)2=2p×12,解得p=2.故抛物线E的方程为x2=4y.
- 6 - / 14
