二次函数最值问题 提升练习(含答案)
图片预览

文档简介
二次函数最值问题提升练习
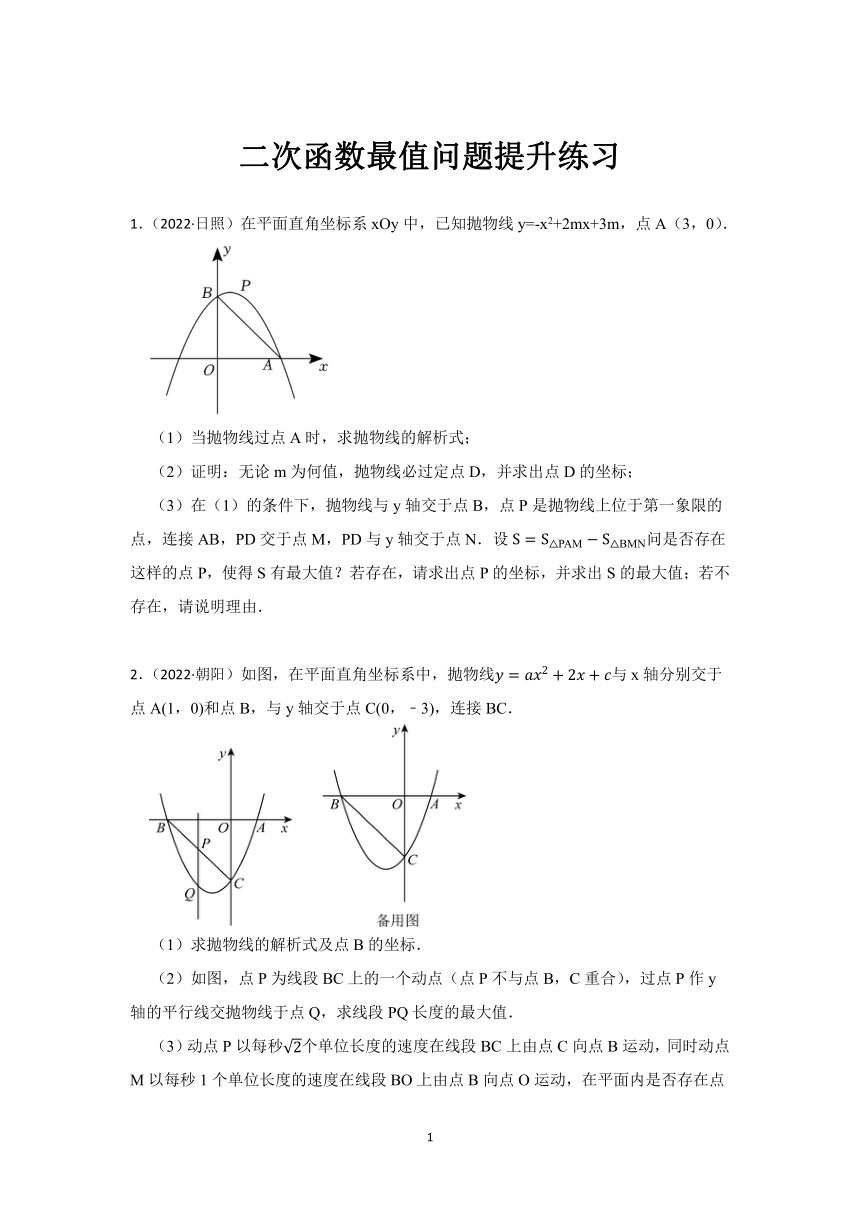
1.(2022·日照)在平面直角坐标系xOy中,已知抛物线y=-x2+2mx+3m,点A(3,0).
(1)当抛物线过点A时,求抛物线的解析式;
(2)证明:无论m为何值,抛物线必过定点D,并求出点D的坐标;
(3)在(1)的条件下,抛物线与y轴交于点B,点P是抛物线上位于第一象限的点,连接AB,PD交于点M,PD与y轴交于点N.设问是否存在这样的点P,使得S有最大值?若存在,请求出点P的坐标,并求出S的最大值;若不存在,请说明理由.
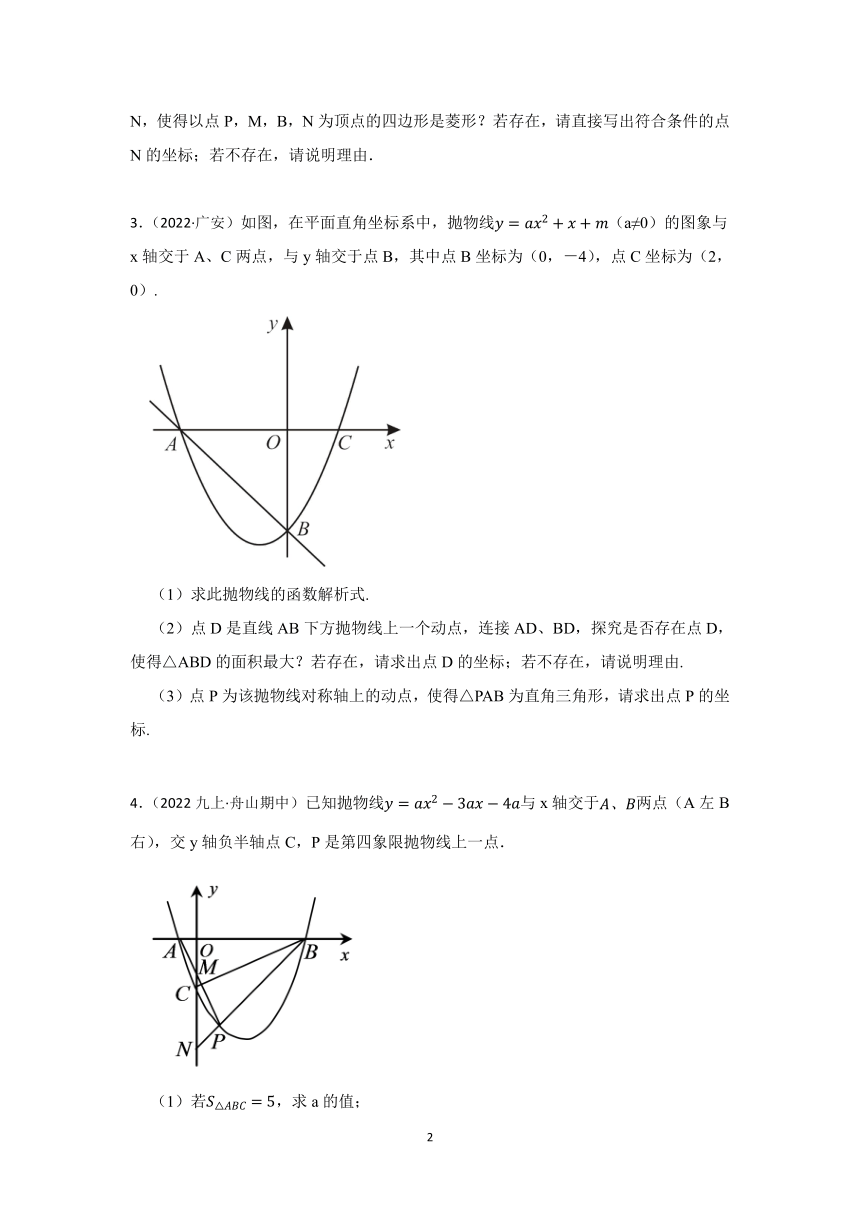
2.(2022·朝阳)如图,在平面直角坐标系中,抛物线与x轴分别交于点A(1,0)和点B,与y轴交于点C(0,﹣3),连接BC.
(1)求抛物线的解析式及点B的坐标.
(2)如图,点P为线段BC上的一个动点(点P不与点B,C重合),过点P作y轴的平行线交抛物线于点Q,求线段PQ长度的最大值.
(3)动点P以每秒个单位长度的速度在线段BC上由点C向点B运动,同时动点M以每秒1个单位长度的速度在线段BO上由点B向点O运动,在平面内是否存在点N,使得以点P,M,B,N为顶点的四边形是菱形?若存在,请直接写出符合条件的点N的坐标;若不存在,请说明理由.
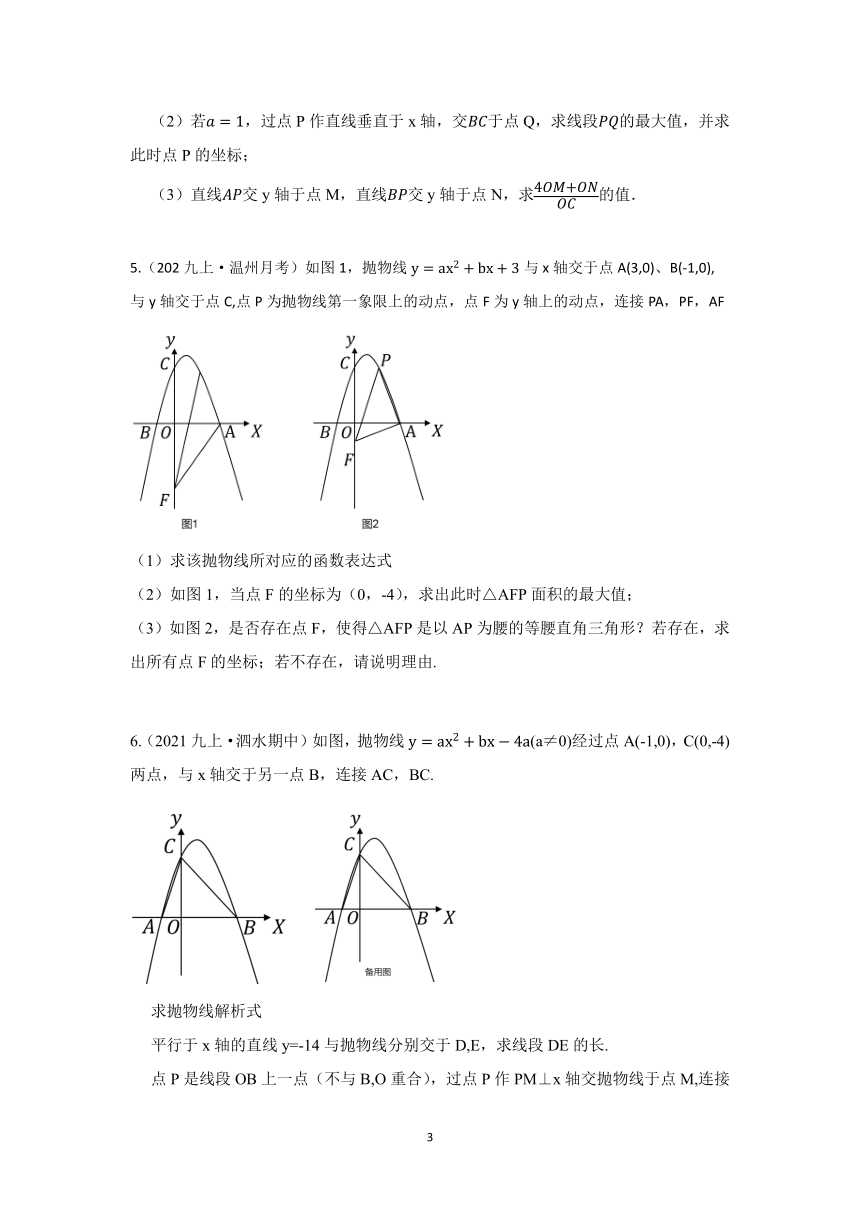
3.(2022·广安)如图,在平面直角坐标系中,抛物线(a≠0)的图象与x轴交于A、C两点,与y轴交于点B,其中点B坐标为(0,-4),点C坐标为(2,0).
(1)求此抛物线的函数解析式.
(2)点D是直线AB下方抛物线上一个动点,连接AD、BD,探究是否存在点D,使得△ABD的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.
(3)点P为该抛物线对称轴上的动点,使得△PAB为直角三角形,请求出点P的坐标.
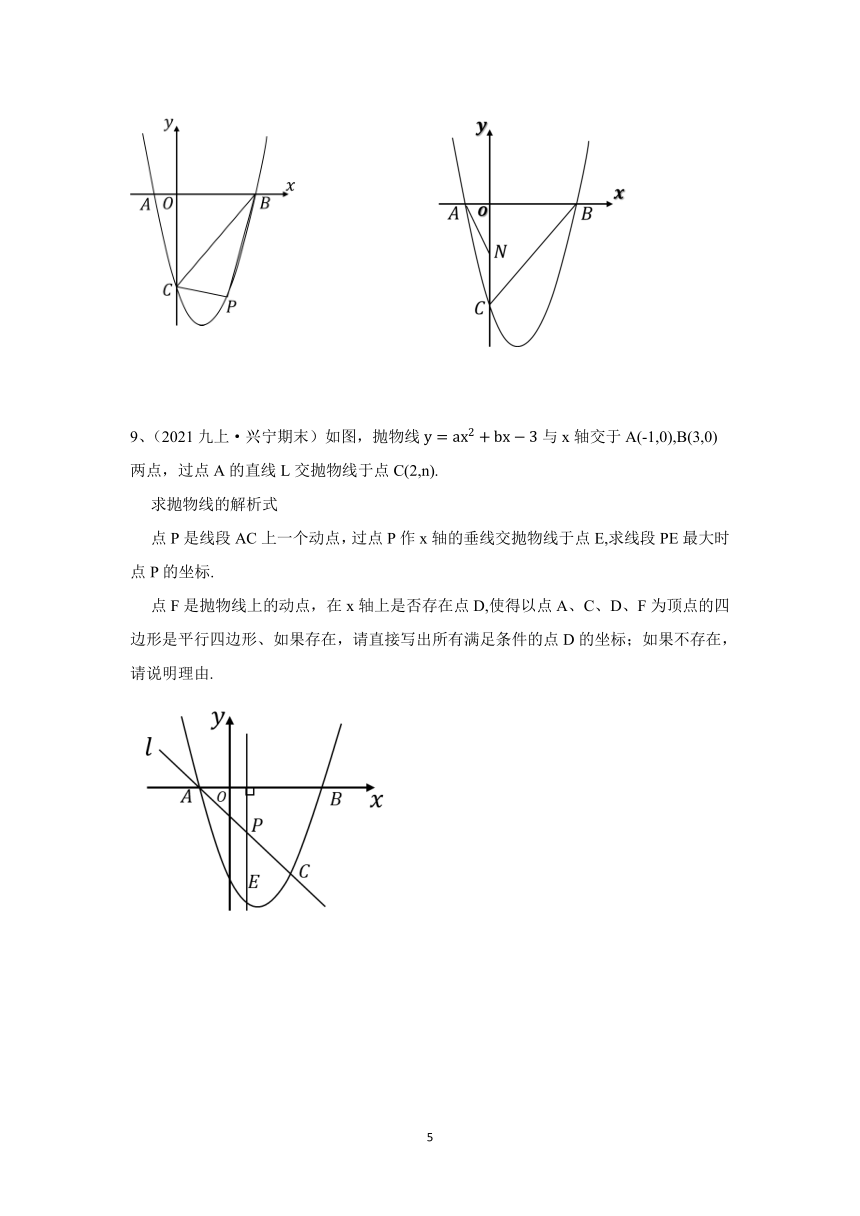
4.(2022九上·舟山期中)已知抛物线与x轴交于两点(A左B右),交y轴负半轴点C,P是第四象限抛物线上一点.
(1)若,求a的值;
(2)若,过点P作直线垂直于x轴,交于点Q,求线段的最大值,并求此时点P的坐标;
(3)直线交y轴于点M,直线交y轴于点N,求的值.
5.(202九上·温州月考)如图1,抛物线与x轴交于点A(3,0)、B(-1,0),
与y轴交于点C,点P为抛物线第一象限上的动点,点F为y轴上的动点,连接PA,PF,AF
(1)求该抛物线所对应的函数表达式
(2)如图1,当点F的坐标为(0,-4),求出此时△AFP面积的最大值;
(3)如图2,是否存在点F,使得△AFP是以AP为腰的等腰直角三角形?若存在,求出所有点F的坐标;若不存在,请说明理由.
6.(2021九上·泗水期中)如图,抛物线(a≠0)经过点A(-1,0),C(0,-4)两点,与x轴交于另一点B,连接AC,BC.
求抛物线解析式
平行于x轴的直线y=-14与抛物线分别交于D,E,求线段DE的长.
点P是线段OB上一点(不与B,O重合),过点P作PM⊥x轴交抛物线于点M,连接CM、BM,求△BCM面积的最大值及此时点M的坐标。
7.(2022九上·鄞州月考)如图,已知抛物线与x轴交于A、B两点,其中点A的坐标为(-3,0),与y轴交于点C,点D(-2,-3)在抛物线上。
(1)求抛物线的表达式
(2)抛物线的对称轴上有一动点P,求△PAD周长的最小值;
(3)抛物线的对称轴上有一动点M,当△MAD是等腰三角形时,直接写出点M的坐标
8.(2021九上·历下期末)如图,在平面直角坐标系XOY中,抛物线与x轴交于A,B两点(B在A的右侧),与y轴交于点C,已知OA=1,OB=4OA,连接BC.
(1)求抛物线的解析式
(2)如图1,点P为BC下方抛物线上一动点,连接BP、CP,当时,求点P的坐标;
(3)如图2,点N为线段OC上一点,求的最小值.
9、(2021九上·兴宁期末)如图,抛物线与x轴交于A(-1,0),B(3,0)两点,过点A的直线L交抛物线于点C(2,n).
求抛物线的解析式
点P是线段AC上一个动点,过点P作x轴的垂线交抛物线于点E,求线段PE最大时点P的坐标.
点F是抛物线上的动点,在x轴上是否存在点D,使得以点A、C、D、F为顶点的四边形是平行四边形、如果存在,请直接写出所有满足条件的点D的坐标;如果不存在,请说明理由.
10、(2021九上·莱芜期末)如图,已知抛物线于x轴交于A(-1,0)、B(3,0)两点,与y轴交于C(0,3).
求抛物线的解析式
点D是第一象限内抛物线上的一个动点(与C、B不重合).过点D作DF⊥X轴于点F,过点D作DM⊥BC,垂足为M,求线段DM的最大值;
已知点P为抛物线对称轴上一动点,若△PBC是直角三角形,求出点P的坐标.
答案解析部分
1.(2022·日照)在平面直角坐标系xOy中,已知抛物线y=-x2+2mx+3m,点A(3,0).
(1)当抛物线过点A时,求抛物线的解析式;
(2)证明:无论m为何值,抛物线必过定点D,并求出点D的坐标;
(3)在(1)的条件下,抛物线与y轴交于点B,点P是抛物线上位于第一象限的点,连接AB,PD交于点M,PD与y轴交于点N.设问是否存在这样的点P,使得S有最大值?若存在,请求出点P的坐标,并求出S的最大值;若不存在,请说明理由.
【答案】(1)解:把x=3,y=0代入y=-x2+2mx+3m得,-9+6m+3m=0,∴m=1,∴y=-x2+2x+3;
(2)证明:∵y=-x2+m(2x+3),∴当2x+3=0时,即时,,∴无论m为何值,抛物线必过定点D,点D的坐标是;
(3)解:如图,
连接OP,设点P(m,-m2+2m+3),设PD的解析式为:y=kx+b,∴,∴,
∴PD的解析式为:y=,当x=0时,y=,∴点N的坐标是(0,),∴,
∵S=S△PAM-S△BMN,∴S=(S△PAM+S四边形AONM)-(S四边形AONM+S△BMN)=S四边形AONP-S△AOB,
∵,
当x=0时,y=-x2+2x+3=3,∴点B的坐标是(0,3),OB=3,,∴==,
∴当时,,当时,,∴点的坐标是(1,4).
【知识点】待定系数法求二次函数解析式;二次函数-动态几何问题
2.(2022·朝阳)如图,在平面直角坐标系中,抛物线与x轴分别交于点A(1,0)和点B,与y轴交于点C(0,﹣3),连接BC.
(1)求抛物线的解析式及点B的坐标.
(2)如图,点P为线段BC上的一个动点(点P不与点B,C重合),过点P作y轴的平行线交抛物线于点Q,求线段PQ长度的最大值.
(3)动点P以每秒个单位长度的速度在线段BC上由点C向点B运动,同时动点M以每秒1个单位长度的速度在线段BO上由点B向点O运动,在平面内是否存在点N,使得以点P,M,B,N为顶点的四边形是菱形?若存在,请直接写出符合条件的点N的坐标;若不存在,请说明理由.
【答案】(1)解:把点A(1,0),C(0,﹣3)代入得:
,解得:,
∴抛物线解析式为;
令 y=0,则,
解得:,
∴点B的坐标为(-3,0)
(2)解:设直线BC的解析式为,
把点B(-3,0),C(0,﹣3)代入得:
,解得:,
∴直线BC的解析式为,
设点,则,
∴,
∴当时,PQ最大,最大值为
(3)解:存在,点N的坐标为或(-2,1)或.
【知识点】待定系数法求二次函数解析式;二次函数与一次函数的综合应用;二次函数-动态几何问题
【解析】【解答】(3)解:存在,
根据题意得:,则,
如图,当BM=PM时,
∵B(-3,0),C(0,-3),
∴OB=OC=3,
∴∠OCB=∠OBC=45°,
延长NP交y轴于点D,
∵点P,M,B,N为顶点的四边形是菱形,
∴PN∥x轴,BN∥PM,即DN⊥y轴,
∴△CDP为等腰直角三角形,
∴,
∵BM=PM,
∴∠MPB=∠OBC=45°,
∴∠PMO=∠PDO=∠MOD=90°,
∴四边形OMPD是矩形,
∴OM=PD=t,MP⊥x轴,
∴BN⊥x轴,
∵BM+OM=OB,
∴t+t=3,解得,
∴,
∴;
如图,当PM=PB时,作PD⊥y轴于D,连接PN,
∵点P,M,B,N为顶点的四边形是菱形,
∴PN⊥BM,NE=PE,
∴BM=2BE,
∴∠OEP=∠DOE=∠ODP=90°,
∴四边形PDOE是矩形,
∴OE=PD=t,
∴BE=3-t,
∴t=2(3-t),解得:t=2,
∴P(-2,-1),
∴N(-2,1);
如图,当PB=MB时,
,解得:,
∴,
过点P作PE⊥x轴于点E,
∴PE⊥PM,
∴∠EON=∠OEP=∠EPN=90°,
∴四边形OEPN为矩形,
∴PN=OE,PN⊥y轴,
∵∠OBC=45°,
∴,
∴,
∴点N在y轴上,
∴,
综上所述,点N的坐标为或(-2,1)或.
3.(2022·广安)如图,在平面直角坐标系中,抛物线(a≠0)的图象与x轴交于A、C两点,与y轴交于点B,其中点B坐标为(0,-4),点C坐标为(2,0).
(1)求此抛物线的函数解析式.
(2)点D是直线AB下方抛物线上一个动点,连接AD、BD,探究是否存在点D,使得△ABD的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.
(3)点P为该抛物线对称轴上的动点,使得△PAB为直角三角形,请求出点P的坐标.
【答案】(1)解:将B(0,-4),C(2,0)代入,
得:,
解得:,
∴抛物线的函数解析式为:.
(2)解:向下平移直线AB,使平移后的直线与抛物线只有唯一公共点D时,此时点D到直线AB的距离最大,此时△ABD的面积最大,
∵时,,,
∴A点坐标为:(-4,0),
设直线AB关系式为:,
将A(-4,0),B(0,-4),代入,
得:,
解得:,
∴直线AB关系式为:,
设直线AB平移后的关系式为:,
则方程有两个相等的实数根,
即有两个相等的实数根,
∴,
即的解为:x=-2,
将x=-2代入抛物线解析式得,,
∴点D的坐标为:(-2,-4)时,△ABD的面积最大;
(3)解:①当∠PAB=90°时,
即PA⊥AB,则设PA所在直线解析式为:,
将A(-4,0)代入得,,
解得:,
∴PA所在直线解析式为:,
∵抛物线对称轴为:x=-1,
∴当x=-1时,,
∴P点坐标为:(-1,3);
②当∠PBA=90°时,
即PB⊥AB,则设PB所在直线解析式为:,
将B(0,-4)代入得,,
∴PA所在直线解析式为:,
∴当x=-1时,,
∴P点坐标为:(-1,-5);
③当∠APB=90°时,设P点坐标为:,
∴PA所在直线斜率为:,PB在直线斜率为:,
∵PA⊥PB,
∴=-1,
解得:,,
∴P点坐标为:,
综上所述,P点坐标为:(-1,3),(-1,-5),,时,△PAB为直角三角形.
【知识点】两一次函数图象相交或平行问题;二次函数与一次函数的综合应用
4(2022九上·舟山期中)已知抛物线与x轴交于两点(A左B右),交y轴负半轴点C,P是第四象限抛物线上一点.
(1)若,求a的值;
(2)若,过点P作直线垂直于x轴,交于点Q,求线段的最大值,并求此时点P的坐标;
(3)直线交y轴于点M,直线交y轴于点N,求的值.
【答案】(1)解:令 ,得 ,解得: , .
∵ 与x轴交于 两点(A左B右),与y轴交于点C,
∴ , , , ,
∵ , ,
解得: ;
(2)解:当 时,抛物线为 ,
将点 、 的坐标代入一次函数表达式可求得:
直线 的表达式为: ,
设点 ,则点 ,
∴ ,
∴当 时, 有最大值4,此时点 ;
(3)解:由(1)知: 、 、 ,
设点 ,
将点P、A的坐标代入一次函数表达式并解得:
直线 的表达式为: ,
故 ,
同理,直线 为 , ,
∴ ,
∵ ,
∴ ,
∴ .
【知识点】二次函数的最值;待定系数法求二次函数解析式;三角形的面积;二次函数与一次函数的综合应用
5(2021九上·温州月考)如图1,抛物线与x轴交于点A(3,0)、B(-1,0),
与y轴交于点C,点P为抛物线第一象限上的动点,点F为y轴上的动点,连接PA,PF,AF
(1)求该抛物线所对应的函数表达式
(2)如图1,当点F的坐标为(0,-4),求出此时△AFP面积的最大值;
(3)如图2,是否存在点F,使得△AFP是以AP为腰的等腰直角三角形?若存在,求出所有点F的坐标;若不存在,请说明理由.
【答案】
(1)将A(3,0),B(-1,0)代入中
由题意得
解得
∴抛物线所对应的函数表达为
(2)∵P为抛物线第一象限上的动点
∴设点P坐标为
连接PO,PA
∵=)=
==6
===
∴=+
===
∵a=
∴抛物线开口向下,函数有最大值
∵0<3
∴当m=时,△AFP面积的最大值为
(3)过P点作PD⊥X轴,垂足为D
设点P坐标为
则
当△AFP是以AP为腰的等腰直角三角形时,
①若∠PAF=90°
由题意得Rt△ADP≌Rt△AOF
∴PD=AO=3
∴=3
解得n=0(不合题意,舍去)或n=2
则OF=AD=OA-OD=1
且点F在y轴上
∴点F坐标为(0,-1)
②若∠APF=90°时
过点P分别向x轴,y轴作PR⊥x轴,PQ⊥y轴
易证Rt△PQF≌Rt△PRA
∴PQ=PR
则
解得(舍去)或
当n=时,P点坐标(,)
∴=
∴)
6(2021九上·泗水期中)如图,抛物线(a≠0)经过点A(-1,0),C(0,4)两点,与x轴交于另一点B,连接AC,BC.
求抛物线解析式
平行于x轴的直线y=-14与抛物线分别交于D,E,求线段DE的长.
点P是线段OB上一点(不与B,O重合),过点P作PM⊥x轴交抛物线于点M,连接CM、BM,求△BCM面积的最大值及此时点M的坐标。
【答案】
将A(-1,0),C(0,4)代入(a≠0)中
由题意得
解得
∴抛物线所对应的函数表达为
联立
由题意得
=-14
解得
∴DE=-=9
线段DE的长为9
设点P的横坐标为m
∵PM⊥x轴,交抛物线于点M
∴M点坐标为(m,)
设直线BC的解析式为
将C(0,4),B(4,0)代入中
解得k=-1,b=4
∴y=-x+4
令PM与直线BC相交于点E
则
∴ME=()=
∴=·EM·OB=×)×4=)
=
∵<0
抛物线开口向下,有最大值
当m=2时,△BCM面积的最大值为2,点M(2,4)
7(2022九上·鄞州月考)如图,已知抛物线与x轴交于A、B两点,其中点A的坐标为(-3,0),与y轴交于点C,点D(-2,-3)在抛物线上。
求抛物线的表达式
抛物线的对称轴上有一动点P,求△PAD周长的最小值;
抛物线的对称轴上有一动点M,当△MAD是等腰三角形时,直接写出点M的坐标
【答案】(1)
(2)
(3)或或或
8(2021九上·历下期末)如图,在平面直角坐标系XOY中,抛物线与x轴交于A,B两点(B在A的右侧),与y轴交于点C,已知OA=1,OB=4OA,连接BC.
求抛物线的解析式
如图1,点P为BC下方抛物线上一动点,连接BP、CP,当时,求点P的坐标;
如图2,点N为线段OC上一点,求的最小值.
【答案】
已知OA=1,OB=4OA,
由题意可知A(-1,0),B(4,0)
将其代入抛物线中
∵
解得a=1,b=-3
∴
过P点作PM//y轴交BC于点M
已知点P是BC下方抛物线上一动点,
设P(m,)
由B(4,0),C(0,-4)求得BC所在直线的解析式为y=x-4
∴M(m,m-4)
∴PM=
∴×)×4=-2+4-4)=-2+8
∵
∴-2+8=8
解得m=2
此时P(2,-8)
(3)过N点向BC作垂线,垂足记为点E
∵tan∠OCB==1
∴∠OCB=45°
∴Rt△NEC为等腰直角三角形
∴=NE
当A,N,E共线时,满足具有最小值
即点A到BC的距离
∵
∴
解得=5
9(2021九上·兴宁期末)如图,抛物线与x轴交于A(-1,0),B(3,0)两点,过点A的直线L交抛物线于点C(2,n).
求抛物线的解析式
点P是线段AC上一个动点,过点P作x轴的垂线交抛物线于点E,求线段PE最大时点P的坐标.
点F是抛物线上的动点,在x轴上是否存在点D,使得以点A、C、D、F为顶点的四边形是平行四边形、如果存在,请直接写出所有满足条件的点D的坐标;如果不存在,请说明理由.
【答案】
(1)
(2)
(3)存在,点D的坐标为或或或
10.(2021九上·莱芜期末)如图,已知抛物线于x轴交于A(-1,0)、B(3,0)两点,与y轴交于C(0,3).
(1)求抛物线的解析式
(2)点D是第一象限内抛物线上的一个动点(与C、B不重合).过点D作DF⊥X轴于点F,过点D作DM⊥BC,垂足为M,求线段DM的最大值;
(3)已知点P为抛物线对称轴上一动点,若△PBC是直角三角形,求出点P的坐标.
【答案】
P点坐标为 或或或
1.(2022·日照)在平面直角坐标系xOy中,已知抛物线y=-x2+2mx+3m,点A(3,0).
(1)当抛物线过点A时,求抛物线的解析式;
(2)证明:无论m为何值,抛物线必过定点D,并求出点D的坐标;
(3)在(1)的条件下,抛物线与y轴交于点B,点P是抛物线上位于第一象限的点,连接AB,PD交于点M,PD与y轴交于点N.设问是否存在这样的点P,使得S有最大值?若存在,请求出点P的坐标,并求出S的最大值;若不存在,请说明理由.
2.(2022·朝阳)如图,在平面直角坐标系中,抛物线与x轴分别交于点A(1,0)和点B,与y轴交于点C(0,﹣3),连接BC.
(1)求抛物线的解析式及点B的坐标.
(2)如图,点P为线段BC上的一个动点(点P不与点B,C重合),过点P作y轴的平行线交抛物线于点Q,求线段PQ长度的最大值.
(3)动点P以每秒个单位长度的速度在线段BC上由点C向点B运动,同时动点M以每秒1个单位长度的速度在线段BO上由点B向点O运动,在平面内是否存在点N,使得以点P,M,B,N为顶点的四边形是菱形?若存在,请直接写出符合条件的点N的坐标;若不存在,请说明理由.
3.(2022·广安)如图,在平面直角坐标系中,抛物线(a≠0)的图象与x轴交于A、C两点,与y轴交于点B,其中点B坐标为(0,-4),点C坐标为(2,0).
(1)求此抛物线的函数解析式.
(2)点D是直线AB下方抛物线上一个动点,连接AD、BD,探究是否存在点D,使得△ABD的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.
(3)点P为该抛物线对称轴上的动点,使得△PAB为直角三角形,请求出点P的坐标.
4.(2022九上·舟山期中)已知抛物线与x轴交于两点(A左B右),交y轴负半轴点C,P是第四象限抛物线上一点.
(1)若,求a的值;
(2)若,过点P作直线垂直于x轴,交于点Q,求线段的最大值,并求此时点P的坐标;
(3)直线交y轴于点M,直线交y轴于点N,求的值.
5.(202九上·温州月考)如图1,抛物线与x轴交于点A(3,0)、B(-1,0),
与y轴交于点C,点P为抛物线第一象限上的动点,点F为y轴上的动点,连接PA,PF,AF
(1)求该抛物线所对应的函数表达式
(2)如图1,当点F的坐标为(0,-4),求出此时△AFP面积的最大值;
(3)如图2,是否存在点F,使得△AFP是以AP为腰的等腰直角三角形?若存在,求出所有点F的坐标;若不存在,请说明理由.
6.(2021九上·泗水期中)如图,抛物线(a≠0)经过点A(-1,0),C(0,-4)两点,与x轴交于另一点B,连接AC,BC.
求抛物线解析式
平行于x轴的直线y=-14与抛物线分别交于D,E,求线段DE的长.
点P是线段OB上一点(不与B,O重合),过点P作PM⊥x轴交抛物线于点M,连接CM、BM,求△BCM面积的最大值及此时点M的坐标。
7.(2022九上·鄞州月考)如图,已知抛物线与x轴交于A、B两点,其中点A的坐标为(-3,0),与y轴交于点C,点D(-2,-3)在抛物线上。
(1)求抛物线的表达式
(2)抛物线的对称轴上有一动点P,求△PAD周长的最小值;
(3)抛物线的对称轴上有一动点M,当△MAD是等腰三角形时,直接写出点M的坐标
8.(2021九上·历下期末)如图,在平面直角坐标系XOY中,抛物线与x轴交于A,B两点(B在A的右侧),与y轴交于点C,已知OA=1,OB=4OA,连接BC.
(1)求抛物线的解析式
(2)如图1,点P为BC下方抛物线上一动点,连接BP、CP,当时,求点P的坐标;
(3)如图2,点N为线段OC上一点,求的最小值.
9、(2021九上·兴宁期末)如图,抛物线与x轴交于A(-1,0),B(3,0)两点,过点A的直线L交抛物线于点C(2,n).
求抛物线的解析式
点P是线段AC上一个动点,过点P作x轴的垂线交抛物线于点E,求线段PE最大时点P的坐标.
点F是抛物线上的动点,在x轴上是否存在点D,使得以点A、C、D、F为顶点的四边形是平行四边形、如果存在,请直接写出所有满足条件的点D的坐标;如果不存在,请说明理由.
10、(2021九上·莱芜期末)如图,已知抛物线于x轴交于A(-1,0)、B(3,0)两点,与y轴交于C(0,3).
求抛物线的解析式
点D是第一象限内抛物线上的一个动点(与C、B不重合).过点D作DF⊥X轴于点F,过点D作DM⊥BC,垂足为M,求线段DM的最大值;
已知点P为抛物线对称轴上一动点,若△PBC是直角三角形,求出点P的坐标.
答案解析部分
1.(2022·日照)在平面直角坐标系xOy中,已知抛物线y=-x2+2mx+3m,点A(3,0).
(1)当抛物线过点A时,求抛物线的解析式;
(2)证明:无论m为何值,抛物线必过定点D,并求出点D的坐标;
(3)在(1)的条件下,抛物线与y轴交于点B,点P是抛物线上位于第一象限的点,连接AB,PD交于点M,PD与y轴交于点N.设问是否存在这样的点P,使得S有最大值?若存在,请求出点P的坐标,并求出S的最大值;若不存在,请说明理由.
【答案】(1)解:把x=3,y=0代入y=-x2+2mx+3m得,-9+6m+3m=0,∴m=1,∴y=-x2+2x+3;
(2)证明:∵y=-x2+m(2x+3),∴当2x+3=0时,即时,,∴无论m为何值,抛物线必过定点D,点D的坐标是;
(3)解:如图,
连接OP,设点P(m,-m2+2m+3),设PD的解析式为:y=kx+b,∴,∴,
∴PD的解析式为:y=,当x=0时,y=,∴点N的坐标是(0,),∴,
∵S=S△PAM-S△BMN,∴S=(S△PAM+S四边形AONM)-(S四边形AONM+S△BMN)=S四边形AONP-S△AOB,
∵,
当x=0时,y=-x2+2x+3=3,∴点B的坐标是(0,3),OB=3,,∴==,
∴当时,,当时,,∴点的坐标是(1,4).
【知识点】待定系数法求二次函数解析式;二次函数-动态几何问题
2.(2022·朝阳)如图,在平面直角坐标系中,抛物线与x轴分别交于点A(1,0)和点B,与y轴交于点C(0,﹣3),连接BC.
(1)求抛物线的解析式及点B的坐标.
(2)如图,点P为线段BC上的一个动点(点P不与点B,C重合),过点P作y轴的平行线交抛物线于点Q,求线段PQ长度的最大值.
(3)动点P以每秒个单位长度的速度在线段BC上由点C向点B运动,同时动点M以每秒1个单位长度的速度在线段BO上由点B向点O运动,在平面内是否存在点N,使得以点P,M,B,N为顶点的四边形是菱形?若存在,请直接写出符合条件的点N的坐标;若不存在,请说明理由.
【答案】(1)解:把点A(1,0),C(0,﹣3)代入得:
,解得:,
∴抛物线解析式为;
令 y=0,则,
解得:,
∴点B的坐标为(-3,0)
(2)解:设直线BC的解析式为,
把点B(-3,0),C(0,﹣3)代入得:
,解得:,
∴直线BC的解析式为,
设点,则,
∴,
∴当时,PQ最大,最大值为
(3)解:存在,点N的坐标为或(-2,1)或.
【知识点】待定系数法求二次函数解析式;二次函数与一次函数的综合应用;二次函数-动态几何问题
【解析】【解答】(3)解:存在,
根据题意得:,则,
如图,当BM=PM时,
∵B(-3,0),C(0,-3),
∴OB=OC=3,
∴∠OCB=∠OBC=45°,
延长NP交y轴于点D,
∵点P,M,B,N为顶点的四边形是菱形,
∴PN∥x轴,BN∥PM,即DN⊥y轴,
∴△CDP为等腰直角三角形,
∴,
∵BM=PM,
∴∠MPB=∠OBC=45°,
∴∠PMO=∠PDO=∠MOD=90°,
∴四边形OMPD是矩形,
∴OM=PD=t,MP⊥x轴,
∴BN⊥x轴,
∵BM+OM=OB,
∴t+t=3,解得,
∴,
∴;
如图,当PM=PB时,作PD⊥y轴于D,连接PN,
∵点P,M,B,N为顶点的四边形是菱形,
∴PN⊥BM,NE=PE,
∴BM=2BE,
∴∠OEP=∠DOE=∠ODP=90°,
∴四边形PDOE是矩形,
∴OE=PD=t,
∴BE=3-t,
∴t=2(3-t),解得:t=2,
∴P(-2,-1),
∴N(-2,1);
如图,当PB=MB时,
,解得:,
∴,
过点P作PE⊥x轴于点E,
∴PE⊥PM,
∴∠EON=∠OEP=∠EPN=90°,
∴四边形OEPN为矩形,
∴PN=OE,PN⊥y轴,
∵∠OBC=45°,
∴,
∴,
∴点N在y轴上,
∴,
综上所述,点N的坐标为或(-2,1)或.
3.(2022·广安)如图,在平面直角坐标系中,抛物线(a≠0)的图象与x轴交于A、C两点,与y轴交于点B,其中点B坐标为(0,-4),点C坐标为(2,0).
(1)求此抛物线的函数解析式.
(2)点D是直线AB下方抛物线上一个动点,连接AD、BD,探究是否存在点D,使得△ABD的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.
(3)点P为该抛物线对称轴上的动点,使得△PAB为直角三角形,请求出点P的坐标.
【答案】(1)解:将B(0,-4),C(2,0)代入,
得:,
解得:,
∴抛物线的函数解析式为:.
(2)解:向下平移直线AB,使平移后的直线与抛物线只有唯一公共点D时,此时点D到直线AB的距离最大,此时△ABD的面积最大,
∵时,,,
∴A点坐标为:(-4,0),
设直线AB关系式为:,
将A(-4,0),B(0,-4),代入,
得:,
解得:,
∴直线AB关系式为:,
设直线AB平移后的关系式为:,
则方程有两个相等的实数根,
即有两个相等的实数根,
∴,
即的解为:x=-2,
将x=-2代入抛物线解析式得,,
∴点D的坐标为:(-2,-4)时,△ABD的面积最大;
(3)解:①当∠PAB=90°时,
即PA⊥AB,则设PA所在直线解析式为:,
将A(-4,0)代入得,,
解得:,
∴PA所在直线解析式为:,
∵抛物线对称轴为:x=-1,
∴当x=-1时,,
∴P点坐标为:(-1,3);
②当∠PBA=90°时,
即PB⊥AB,则设PB所在直线解析式为:,
将B(0,-4)代入得,,
∴PA所在直线解析式为:,
∴当x=-1时,,
∴P点坐标为:(-1,-5);
③当∠APB=90°时,设P点坐标为:,
∴PA所在直线斜率为:,PB在直线斜率为:,
∵PA⊥PB,
∴=-1,
解得:,,
∴P点坐标为:,
综上所述,P点坐标为:(-1,3),(-1,-5),,时,△PAB为直角三角形.
【知识点】两一次函数图象相交或平行问题;二次函数与一次函数的综合应用
4(2022九上·舟山期中)已知抛物线与x轴交于两点(A左B右),交y轴负半轴点C,P是第四象限抛物线上一点.
(1)若,求a的值;
(2)若,过点P作直线垂直于x轴,交于点Q,求线段的最大值,并求此时点P的坐标;
(3)直线交y轴于点M,直线交y轴于点N,求的值.
【答案】(1)解:令 ,得 ,解得: , .
∵ 与x轴交于 两点(A左B右),与y轴交于点C,
∴ , , , ,
∵ , ,
解得: ;
(2)解:当 时,抛物线为 ,
将点 、 的坐标代入一次函数表达式可求得:
直线 的表达式为: ,
设点 ,则点 ,
∴ ,
∴当 时, 有最大值4,此时点 ;
(3)解:由(1)知: 、 、 ,
设点 ,
将点P、A的坐标代入一次函数表达式并解得:
直线 的表达式为: ,
故 ,
同理,直线 为 , ,
∴ ,
∵ ,
∴ ,
∴ .
【知识点】二次函数的最值;待定系数法求二次函数解析式;三角形的面积;二次函数与一次函数的综合应用
5(2021九上·温州月考)如图1,抛物线与x轴交于点A(3,0)、B(-1,0),
与y轴交于点C,点P为抛物线第一象限上的动点,点F为y轴上的动点,连接PA,PF,AF
(1)求该抛物线所对应的函数表达式
(2)如图1,当点F的坐标为(0,-4),求出此时△AFP面积的最大值;
(3)如图2,是否存在点F,使得△AFP是以AP为腰的等腰直角三角形?若存在,求出所有点F的坐标;若不存在,请说明理由.
【答案】
(1)将A(3,0),B(-1,0)代入中
由题意得
解得
∴抛物线所对应的函数表达为
(2)∵P为抛物线第一象限上的动点
∴设点P坐标为
连接PO,PA
∵=)=
==6
===
∴=+
===
∵a=
∴抛物线开口向下,函数有最大值
∵0<3
∴当m=时,△AFP面积的最大值为
(3)过P点作PD⊥X轴,垂足为D
设点P坐标为
则
当△AFP是以AP为腰的等腰直角三角形时,
①若∠PAF=90°
由题意得Rt△ADP≌Rt△AOF
∴PD=AO=3
∴=3
解得n=0(不合题意,舍去)或n=2
则OF=AD=OA-OD=1
且点F在y轴上
∴点F坐标为(0,-1)
②若∠APF=90°时
过点P分别向x轴,y轴作PR⊥x轴,PQ⊥y轴
易证Rt△PQF≌Rt△PRA
∴PQ=PR
则
解得(舍去)或
当n=时,P点坐标(,)
∴=
∴)
6(2021九上·泗水期中)如图,抛物线(a≠0)经过点A(-1,0),C(0,4)两点,与x轴交于另一点B,连接AC,BC.
求抛物线解析式
平行于x轴的直线y=-14与抛物线分别交于D,E,求线段DE的长.
点P是线段OB上一点(不与B,O重合),过点P作PM⊥x轴交抛物线于点M,连接CM、BM,求△BCM面积的最大值及此时点M的坐标。
【答案】
将A(-1,0),C(0,4)代入(a≠0)中
由题意得
解得
∴抛物线所对应的函数表达为
联立
由题意得
=-14
解得
∴DE=-=9
线段DE的长为9
设点P的横坐标为m
∵PM⊥x轴,交抛物线于点M
∴M点坐标为(m,)
设直线BC的解析式为
将C(0,4),B(4,0)代入中
解得k=-1,b=4
∴y=-x+4
令PM与直线BC相交于点E
则
∴ME=()=
∴=·EM·OB=×)×4=)
=
∵<0
抛物线开口向下,有最大值
当m=2时,△BCM面积的最大值为2,点M(2,4)
7(2022九上·鄞州月考)如图,已知抛物线与x轴交于A、B两点,其中点A的坐标为(-3,0),与y轴交于点C,点D(-2,-3)在抛物线上。
求抛物线的表达式
抛物线的对称轴上有一动点P,求△PAD周长的最小值;
抛物线的对称轴上有一动点M,当△MAD是等腰三角形时,直接写出点M的坐标
【答案】(1)
(2)
(3)或或或
8(2021九上·历下期末)如图,在平面直角坐标系XOY中,抛物线与x轴交于A,B两点(B在A的右侧),与y轴交于点C,已知OA=1,OB=4OA,连接BC.
求抛物线的解析式
如图1,点P为BC下方抛物线上一动点,连接BP、CP,当时,求点P的坐标;
如图2,点N为线段OC上一点,求的最小值.
【答案】
已知OA=1,OB=4OA,
由题意可知A(-1,0),B(4,0)
将其代入抛物线中
∵
解得a=1,b=-3
∴
过P点作PM//y轴交BC于点M
已知点P是BC下方抛物线上一动点,
设P(m,)
由B(4,0),C(0,-4)求得BC所在直线的解析式为y=x-4
∴M(m,m-4)
∴PM=
∴×)×4=-2+4-4)=-2+8
∵
∴-2+8=8
解得m=2
此时P(2,-8)
(3)过N点向BC作垂线,垂足记为点E
∵tan∠OCB==1
∴∠OCB=45°
∴Rt△NEC为等腰直角三角形
∴=NE
当A,N,E共线时,满足具有最小值
即点A到BC的距离
∵
∴
解得=5
9(2021九上·兴宁期末)如图,抛物线与x轴交于A(-1,0),B(3,0)两点,过点A的直线L交抛物线于点C(2,n).
求抛物线的解析式
点P是线段AC上一个动点,过点P作x轴的垂线交抛物线于点E,求线段PE最大时点P的坐标.
点F是抛物线上的动点,在x轴上是否存在点D,使得以点A、C、D、F为顶点的四边形是平行四边形、如果存在,请直接写出所有满足条件的点D的坐标;如果不存在,请说明理由.
【答案】
(1)
(2)
(3)存在,点D的坐标为或或或
10.(2021九上·莱芜期末)如图,已知抛物线于x轴交于A(-1,0)、B(3,0)两点,与y轴交于C(0,3).
(1)求抛物线的解析式
(2)点D是第一象限内抛物线上的一个动点(与C、B不重合).过点D作DF⊥X轴于点F,过点D作DM⊥BC,垂足为M,求线段DM的最大值;
(3)已知点P为抛物线对称轴上一动点,若△PBC是直角三角形,求出点P的坐标.
【答案】
P点坐标为 或或或
