2021-2022学年黑龙江省黑河二中七年级(上)期末数学试卷(word,含解析)
文档属性
| 名称 | 2021-2022学年黑龙江省黑河二中七年级(上)期末数学试卷(word,含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 262.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-29 08:24:06 | ||
图片预览




文档简介
2021-2022学年黑龙江省黑河二中七年级(上)期末数学试卷
一、单项选择题(每小题3分,共30分)
1.﹣2的绝对值是( )
A.2 B.﹣2 C. D.﹣
2.下列各数中,比﹣3小的数是( )
A.﹣5 B.﹣1 C.0 D.1
3.计算:的结果为( )
A.﹣5 B.5 C. D.
4.下列各组中,不是同类项的是( )
A.a和﹣a B.3和﹣2 C.3mn和﹣5nm D.﹣x2y和2xy2
5.古埃及人的“纸草书”中记载了一个数学问题:一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33.若设这个数是x,则所列方程为( )
A.x+x+x=33 B.x+x+x=33
C.x+x+x+x=33 D.x+x+x﹣x=33
6.已知A,B两点都在数轴上,点A所表示的数是a,点B所表示的数是b,并且a=﹣1,AB=3,则( )
A.b=2 B.b=﹣4 C.b=2或b=﹣4 D.b=﹣3
7.如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOE的度数等于( )
A.145° B.135° C.35° D.120°
8.若|x|=7,|y|=5,且x+y>0,那么x﹣y的值是( )
A.2或12 B.2或﹣12 C.﹣2或12 D.﹣2或﹣12
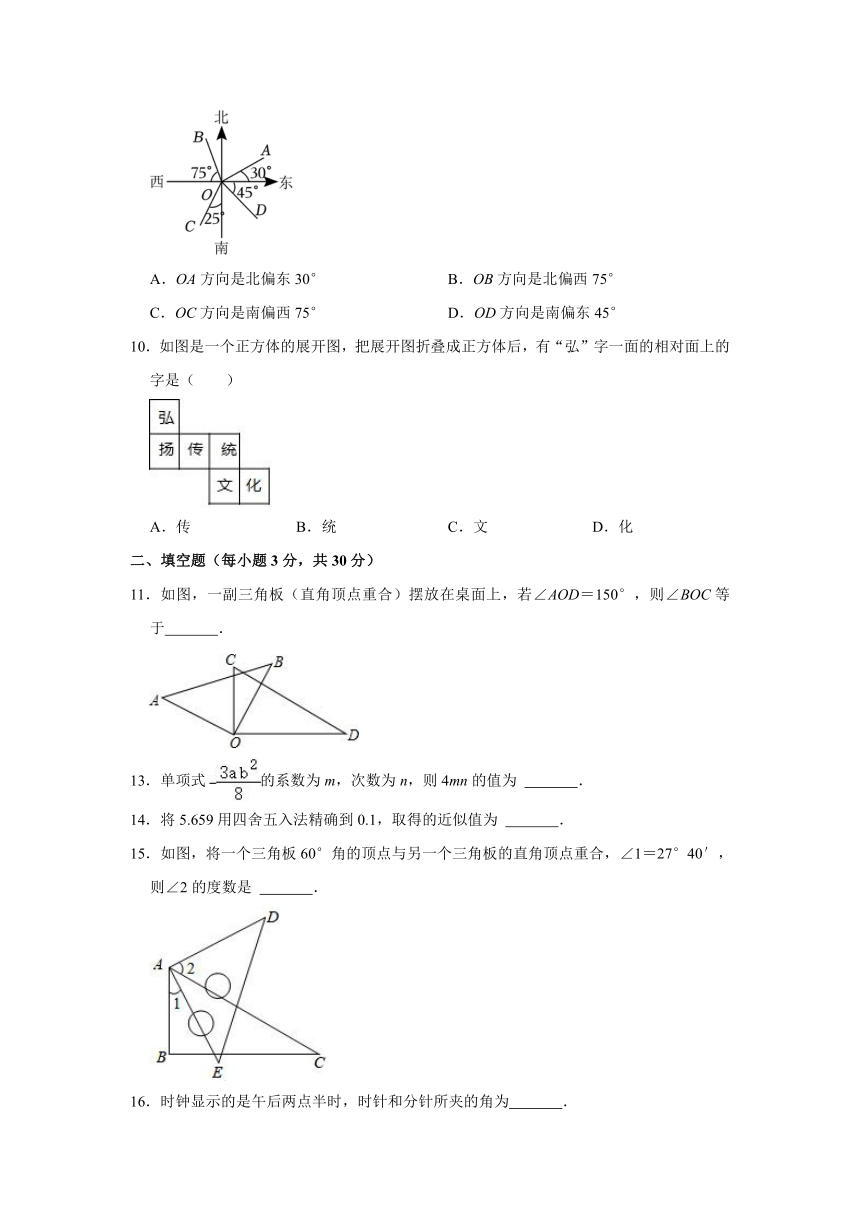
9.如图,下列说法中正确的是( )
A.OA方向是北偏东30° B.OB方向是北偏西75°
C.OC方向是南偏西75° D.OD方向是南偏东45°
10.如图是一个正方体的展开图,把展开图折叠成正方体后,有“弘”字一面的相对面上的字是( )
A.传 B.统 C.文 D.化
二、填空题(每小题3分,共30分)
11.如图,一副三角板(直角顶点重合)摆放在桌面上,若∠AOD=150°,则∠BOC等于 .
13.单项式的系数为m,次数为n,则4mn的值为 .
14.将5.659用四舍五入法精确到0.1,取得的近似值为 .
15.如图,将一个三角板60°角的顶点与另一个三角板的直角顶点重合,∠1=27°40′,则∠2的度数是 .
16.时钟显示的是午后两点半时,时针和分针所夹的角为 .
17.如果a、b互为倒数,c、d互为相反数,且m=1,则代数式2ab﹣(c+d)+m2= .
18.修建公路时,需要将弯曲的道路改直,用数学知识解释为 .
19.多项式x2﹣3kxy﹣3y2+6xy﹣8不含xy项,则k= .
20.如图,由边长相等的黑、白两种颜色的正方形按照一定规律拼接而成,依此规律,第n个图案中白色正方形的个数为 .
三、解答题(共60分)
21.(10分)计算:
(1)﹣62×(﹣)+23÷(﹣);
(2)﹣22×3+(﹣10)÷(﹣2).
22.(5分)先化简,再求值5x2+(4﹣5x﹣3x2)﹣(2x2﹣6x+5),其中x=﹣3.
23.(10分)解方程:
(1)2﹣3(x+1)=1﹣2(1+0.5x);
(2)+1=.
24.(5分)一个角的补角比它的余角的2倍大20°,求这个角的度数.
25.(8分)已知:锐角∠AOB.
(1)若∠AOB=65°,则∠AOB的余角的度数为 度.
(2)若∠AOB=53°17 ,则∠AOB的补角的度数为 .
(3)若∠AOB=31°12 ,计算:∠AOB= .
(4)若∠AOB=20°21 ,计算:3∠AOB.
26.(8分)A,B两地相距150千米,甲车从A地匀速行驶前往B地,每小时行驶40千米;乙车从B地匀速行驶前往A地,每小时行驶60千米.
(1)甲、乙两车同时出发, 小时相遇.
(2)甲、乙两车同时出发, 小时两车相距10千米.
(3)若乙车先行驶半小时,甲车再出发,求甲车出发几小时两车相遇?
27.(6分)如图,线段AB=20,点C是线段AB的中点,点D是线段BC的中点,点E在线段AC上,并且CE=AC.
(1)求线段DB的长.
(2)求线段ED的长.
28.(8分)如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF上的B'处,得到折痕EC,将∠AEF对折,点A落在直线EF上的点A'处,得到折痕EN.
(1)若∠BEC=60°,则∠B'EC= °,∠A'EN= °,∠CEN= °;
(2)若∠BEC=m°,则(1)中∠CEN的值是否改变?∠CEN的度数是多少?请说明你的理由.
2021-2022学年黑龙江省黑河二中七年级(上)期末数学试卷
参考答案与试题解析
一、单项选择题(每小题3分,共30分)
1.﹣2的绝对值是( )
A.2 B.﹣2 C. D.﹣
【分析】根据负数的绝对值等于它的相反数解答.
【解答】解:﹣2的绝对值是2,
即|﹣2|=2.
故选:A.
【点评】本题考查了绝对值的性质:正数的绝对值是它本身;负数的绝对值是它的相反数;0的绝对值是0.
2.下列各数中,比﹣3小的数是( )
A.﹣5 B.﹣1 C.0 D.1
【分析】有理数大小比较的法则:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小,据此判断即可.
【解答】解:﹣5<﹣3<﹣1<0<1,
所以比﹣3小的数是﹣5,
故选:A.
【点评】此题主要考查了有理数大小比较的方法,要熟练掌握,解答此题的关键是要明确:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小.
3.计算:的结果为( )
A.﹣5 B.5 C. D.
【分析】根据有理数的乘除法法则,按照运算顺序,从左往右计算即可.
【解答】解:原式=1×(﹣)
=﹣,
故选:C.
【点评】本题考查了有理数的乘除法法则,掌握同级运算的运算顺序是从左往右是解题的关键.
4.下列各组中,不是同类项的是( )
A.a和﹣a B.3和﹣2 C.3mn和﹣5nm D.﹣x2y和2xy2
【分析】根据同类项的定义(所含字母相同,并且相同字母的指数也相同,这样的项叫做同类项)即可作出判断.
【解答】解:A.a和﹣a所含字母相同,相同字母的指数相同,是同类项,故此选项不符合题意;
B.3和﹣2是同类项,故此选项不符合题意;
C.3mn和﹣5nm所含字母相同,相同字母的指数相同,是同类项,故此选项不符合题意;
D.﹣x2y和2xy2所含字母相同,但相同字母的指数不同,不是同类项,故此选项符合题意.
故选:D.
【点评】本题考查了同类项,掌握同类项的定义是解答本题的关键.
5.古埃及人的“纸草书”中记载了一个数学问题:一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33.若设这个数是x,则所列方程为( )
A.x+x+x=33 B.x+x+x=33
C.x+x+x+x=33 D.x+x+x﹣x=33
【分析】根据题意列方程x+x+x+x=33.
【解答】解:由题意可得x+x+x+x=33.
故选:C.
【点评】本题考查列一元一次方程,解题关键是通过题干找出等量关系.
6.已知A,B两点都在数轴上,点A所表示的数是a,点B所表示的数是b,并且a=﹣1,AB=3,则( )
A.b=2 B.b=﹣4 C.b=2或b=﹣4 D.b=﹣3
【分析】分两种情况:点B在A的左边或右边,列式计算可得答案.
【解答】解:当点B在A的左边时,b=﹣1﹣3=﹣4,
当点B在A的右边时,b=﹣1+3=2;
故选:C.
【点评】本题考查了数轴上两点间的距离,注意分情况讨论是解题关键.
7.如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOE的度数等于( )
A.145° B.135° C.35° D.120°
【分析】根据角平分线的性质可得∠EOA的度数,然后根据补角定义可得答案.
【解答】解:∵OA平分∠EOC,∠EOC=70°,
∴∠EOA=35°,
∴∠BOE=180°﹣35°=145°,
故选:A.
【点评】此题主要考查了角平分线的定义,以及补角定义,关键是掌握角平分线把角分成相等的两部分.
8.若|x|=7,|y|=5,且x+y>0,那么x﹣y的值是( )
A.2或12 B.2或﹣12 C.﹣2或12 D.﹣2或﹣12
【分析】题中给出了x,y的绝对值,可求出x,y的值;再根据x+y>0,分类讨论,求x﹣y的值.
【解答】解:∵|x|=7,|y|=5,
∴x=±7,y=±5.
又x+y>0,则x,y同为正数或x,y异号,但正数的绝对值较大,
∴x=7,y=5或x=7,y=﹣5.
∴x﹣y=2或12.
故选:A.
【点评】理解绝对值的概念,同时要熟练运用有理数的减法运算法则.
9.如图,下列说法中正确的是( )
A.OA方向是北偏东30° B.OB方向是北偏西75°
C.OC方向是南偏西75° D.OD方向是南偏东45°
【分析】根据方向角的概念解答即可.
【解答】解:A、OA方向是北偏东60°,不合题意;
B、OB方向是北偏西15°,不合题意;
C、OC方向是南偏西25°,不合题意;
D、符合题意.
故选:D.
【点评】此题很简单,只要熟知方向角的定义便可解答.
10.如图是一个正方体的展开图,把展开图折叠成正方体后,有“弘”字一面的相对面上的字是( )
A.传 B.统 C.文 D.化
【分析】利用正方体及其表面展开图的特点解题.
【解答】解:这是一个正方体的平面展开图,共有六个面,其中面“扬”与“统”相对,面“弘”与面“文”相对,“传”与面“化”相对.
故选:C.
【点评】本题考查了正方体的展开图得知识,注意正方体的空间图形,从相对面入手,分析及解答问题.
二、填空题(每小题3分,共30分)
11.如图,一副三角板(直角顶点重合)摆放在桌面上,若∠AOD=150°,则∠BOC等于 30° .
【分析】从如图可以看出,∠BOC的度数正好是两直角相加减去∠AOD的度数,从而问题可解.
【解答】解:∵∠AOB=∠COD=90°,∠AOD=150°
∴∠BOC=∠AOB+∠COD﹣∠AOD=90°+90°﹣150°=30°.
故答案为:30°
【点评】此题主要考查学生对角的计算的理解和掌握,解答此题的关键是让学生通过观察图示,发现几个角之间的关系.
13.单项式的系数为m,次数为n,则4mn的值为 .
【分析】根据单项式的系数是数字部分,可得系数m,根据单项式的次数是字母指数和,可得次数n,代入计算可得答案.
【解答】解:∵单项式的系数为m,次数为n,
∴m=﹣,n=1+2=3,
∴4m n=4×(﹣)×3=﹣,
故答案为:﹣.
【点评】本题考查了单项式的定义,确定单项式的系数和次数时,把一个单项式分解成数字因数和字母因式的积,是找准单项式的系数和次数的关键.
14.将5.659用四舍五入法精确到0.1,取得的近似值为 5.7 .
【分析】对百分位数字5四舍五入即可.
【解答】解:将5.659用四舍五入法精确到0.1,取得的近似值为5.7,
故答案为:5.7.
【点评】本题考查了近似数和有效数字:近似数与精确数的接近程度,可以用精确度表示.一般有,精确到哪一位,保留几个有效数字等说法.
15.如图,将一个三角板60°角的顶点与另一个三角板的直角顶点重合,∠1=27°40′,则∠2的度数是 57°40′ .
【分析】根据∠BAC=60°,∠1=27°40′,求出∠EAC的度数,再根据∠2=90°﹣∠EAC,即可求出∠2的度数.
【解答】解:∵∠BAC=60°,∠1=27°40′,
∴∠EAC=60°﹣27°40′=32°20′,
∵∠EAD=90°,
∴∠2=90°﹣∠EAC=90°﹣32°20′=57°40′;
故答案为:57°40′.
【点评】本题主要考查了度分秒的换算,解题的关键是能够正确求出∠EAC的度数.
16.时钟显示的是午后两点半时,时针和分针所夹的角为 105° .
【分析】先分别求出时针和分钟转过的角度,再相减即可.
【解答】解:时针转过的角度是(2+)×30°=75°,
分钟转过的角度是30×6°=180°,
所以钟表在2点半时,其时针和分针所成的角是180°﹣75°=105°,
故答案为:105°.
【点评】本考查了钟面角,能知道时针每小时转30°、分钟每分钟转6°是解此题的关键.
17.如果a、b互为倒数,c、d互为相反数,且m=1,则代数式2ab﹣(c+d)+m2= 3 .
【分析】由题意可知:ab=1,c+d=0,然后代入数值进行计算即可.
【解答】解:∵a、b互为倒数,c、d互为相反数,
∴ab=1,c+d=0.
将ab=1,c+d=0,m=1代入得:原式=2×1﹣0+12=3.
故答案为:3.
【点评】本题主要考查的是求代数式的值,求得ab=1,c+d=0是解题的关键.
18.修建公路时,需要将弯曲的道路改直,用数学知识解释为 两点之间线段最短 .
【分析】根据两点之间线段最短解答.
【解答】解:需要将弯曲的道路改直,用数学知识解释为:两点之间线段最短.
故答案为:两点之间线段最短.
【点评】本题考查了线段的性质,是基础题,熟记两点之间线段最短是解题的关键.
19.多项式x2﹣3kxy﹣3y2+6xy﹣8不含xy项,则k= 2 .
【分析】先将原多项式合并同类项,再令xy项的系数为0,然后解关于k的方程即可求出k.
【解答】解:原式=x2+(﹣3k+6)xy﹣3y2﹣8,
因为不含xy项,
故﹣3k+6=0,
解得:k=2.
故答案为:2.
【点评】本题考查了合并同类项法则及对多项式“项”的概念的理解,题目设计巧妙,有利于培养学生灵活运用知识的能力.
20.如图,由边长相等的黑、白两种颜色的正方形按照一定规律拼接而成,依此规律,第n个图案中白色正方形的个数为 5n+3 .
【分析】根据图形的变化,找出变化规律,再求值即可.
【解答】解:根据题意有,
第1个图案中白色正方形的个数为:3+5×1=8,
第2个图案中白色正方形的个数为:3+5×2=13,
第3个图案中白色正方形的个数为:3+5×3=18,
……,
第n个图案中白色正方形的个数为:3+5×n=5n+3.
故答案为:5n+3.
【点评】本题考查了图形的变化,根据图形的变化找出其规律再求值是解本题的关键,综合性较强,难度适中.
三、解答题(共60分)
21.(10分)计算:
(1)﹣62×(﹣)+23÷(﹣);
(2)﹣22×3+(﹣10)÷(﹣2).
【分析】(1)先算乘方,再算乘除,后算加减,有括号先算括号里,即可解答;
(2)先算乘方,再算乘除,后算加减,即可解答.
【解答】解:(1)﹣62×(﹣)+23÷(﹣)
=﹣36×(﹣)+8×(﹣)
=6+(﹣20)
=﹣14;
(2)﹣22×3+(﹣10)÷(﹣2)
=﹣4×3+5
=﹣12+5
=﹣7.
【点评】本题考查了有理数的混合运算,准确熟练地进行计算是解题的关键.
22.(5分)先化简,再求值5x2+(4﹣5x﹣3x2)﹣(2x2﹣6x+5),其中x=﹣3.
【分析】根据整式的加减法则即可得出答案.
【解答】解:原式=5x2+4﹣5x﹣3x2﹣2x2+6x﹣5
=x﹣1,
当x=﹣3时,
原式=﹣3﹣1=﹣4.
【点评】本题主要考查整式的化简求值,关键是要牢记去括号的法则和合并同类项的原理.
23.(10分)解方程:
(1)2﹣3(x+1)=1﹣2(1+0.5x);
(2)+1=.
【分析】(1)按照解一元一次方程的步骤:去括号,移项,合并同类项,系数化为1,进行计算即可解答;
(2)按照解一元一次方程的步骤:去分母,去括号,移项,合并同类项,系数化为1,进行计算即可解答.
【解答】解:(1)2﹣3(x+1)=1﹣2(1+0.5x),
2﹣3x﹣3=1﹣2﹣x,
﹣3x+x=1﹣2﹣2+3,
﹣2x=0,
x=0;
(2)+1=,
2(2x﹣1)+6=2x+1,
4x﹣2+6=2x+1,
4x﹣2x=1+2﹣6,
2x=﹣3,
x=﹣1.5.
【点评】本题考查了解一元一次方程,熟练掌握解一元一次方程的步骤是解题的关键.
24.(5分)一个角的补角比它的余角的2倍大20°,求这个角的度数.
【分析】设出所求的角为x,则它的补角为180°﹣x,余角为90°﹣x,根据题意列出方程,再解方程即可,
【解答】解:设这个角的度数是x,则它的补角为:180°﹣x,余角为90°﹣x;
由题意,得:(180°﹣x)﹣2(90°﹣x)=20°.
解得:x=20°.
答:这个角的度数是20°.
【点评】本题考查了余角和补角的定义;根据角之间的互余和互补关系列出方程是解决问题的关键.
25.(8分)已知:锐角∠AOB.
(1)若∠AOB=65°,则∠AOB的余角的度数为 25 度.
(2)若∠AOB=53°17 ,则∠AOB的补角的度数为 126°43 .
(3)若∠AOB=31°12 ,计算:∠AOB= 15°36′ .
(4)若∠AOB=20°21 ,计算:3∠AOB.
【分析】(1)根据余角的定义可得结论;
(2)根据补角的定义可得结论;
(3)根据角的倍数关系可得结论;
(4)根据角的倍数关系可得结论.
【解答】解:(1)∠AOB的余角的度数为90°﹣65°=25°;
(2)∠AOB的补角的度数为180°﹣53°17′=126°43 ;
(3)∵∠AOB=31°12 ,
∴∠AOB=×31°12′=×30°72′=15°36′;
(4)∵∠AOB=20°21 ,
∴3∠AOB=3×20°21
=60°63
=61°3 .
【点评】此题考查的是余角和补角的性质,正确计算是关键.
26.(8分)A,B两地相距150千米,甲车从A地匀速行驶前往B地,每小时行驶40千米;乙车从B地匀速行驶前往A地,每小时行驶60千米.
(1)甲、乙两车同时出发, 1.5 小时相遇.
(2)甲、乙两车同时出发, 1.4或1.6 小时两车相距10千米.
(3)若乙车先行驶半小时,甲车再出发,求甲车出发几小时两车相遇?
【分析】(1)设甲、乙两车同时出发,x小时相遇,依据时间=路程÷速度列出方程即可解答,
(1)分两种情况:相遇前两车相距10千米和相遇后两车相距10千米.
(2)设甲车出发y小时后两车相遇,根据A、B两地距离是150米列出方程并解答.
【解答】解:(1)设甲、乙两车同时出发,x小时相遇,
依题意得:(60+40)x=150,
解得x=1.5,
即甲、乙两车同时出发,1.5小时相遇,
故答案为:1.5;
(2)设甲、乙两车同时出发,n小时后两车相距10千米,
①相遇前两车相距10千米,
依题意得:(60+40)n+10=150,
解得n=1.4,
即甲、乙两车同时出发,1.4小时后两车相距10千米;
②相遇后两车相距10千米,
依题意得:(60+40)n﹣10=150,
解得n=1.6
即甲、乙两车同时出发,1.6小时后两车相距10千米;
综上所述,甲、乙两车同时出发,1.4或1.6小时后两车相距10千米,
故答案为:1.4或1.6;
(3)设甲车出发y小时两车相遇,根据题意,得
40y+60y+60×0.5=150.
解得 x=1.2.
∴甲车出发1.2小时两车相遇.
【点评】本题考查了一元一次方程的应用.解答(2)题,要分类讨论,以防漏解.
27.(6分)如图,线段AB=20,点C是线段AB的中点,点D是线段BC的中点,点E在线段AC上,并且CE=AC.
(1)求线段DB的长.
(2)求线段ED的长.
【分析】(1)根据线段中点的性质,可得DC与BC的关系,CE与AC的关系,根据线段的和差,可得答案;
(2)根据线段中点的性质,可得BC的长,可得AC与BC的关系,可得DC的长,根据线段的和差,可得答案.
【解答】解:(1)∵点C是线段AB的中点,
∴AC=BC=×20=10,
∵点D是线段BC的中点,
∴DB=CD=BC=5;
(2)∵CE=AC,
∴CE=×10=4,
∴ED=CE+CD=4+5=9.
【点评】本题考查了两点间的距离,利用线段中点的性质,线段的和差是解题关键.
28.(8分)如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF上的B'处,得到折痕EC,将∠AEF对折,点A落在直线EF上的点A'处,得到折痕EN.
(1)若∠BEC=60°,则∠B'EC= 60 °,∠A'EN= 30 °,∠CEN= 90 °;
(2)若∠BEC=m°,则(1)中∠CEN的值是否改变?∠CEN的度数是多少?请说明你的理由.
【分析】(1)由折叠的性质和∠BEC的度数可得出结论;
(2)解法同(1)过程即可得出结论.
【解答】解:(1)由折叠可知∠BEC=∠B′EC=∠BEB′,∠AEN=∠A′EN=∠AEA′,
∵∠BEC=60°,
∴∠B′EC=60°,
∵∠BEB′+∠AEA′=180°,
∴∠CEN=∠A′EN+∠B′EC=∠BEB′+∠AEA′=90°,
∴∠A′EN=30°,
故答案为:60°,30°,90°.
(2)∠CEN的度数不变,∠CEN=90°,理由如下:
由折叠可知∠BEC=∠B′EC=∠BEB′,∠AEN=∠A′EN=∠AEA′,
∴∠CEN=∠A′EN+∠B′EC=∠BEB′+∠AEA′=90°.
【点评】本题考查了角的计算、折叠的性质以及平行线的性质等知识;熟练掌握对折和平行线的性质是解题的关键.
一、单项选择题(每小题3分,共30分)
1.﹣2的绝对值是( )
A.2 B.﹣2 C. D.﹣
2.下列各数中,比﹣3小的数是( )
A.﹣5 B.﹣1 C.0 D.1
3.计算:的结果为( )
A.﹣5 B.5 C. D.
4.下列各组中,不是同类项的是( )
A.a和﹣a B.3和﹣2 C.3mn和﹣5nm D.﹣x2y和2xy2
5.古埃及人的“纸草书”中记载了一个数学问题:一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33.若设这个数是x,则所列方程为( )
A.x+x+x=33 B.x+x+x=33
C.x+x+x+x=33 D.x+x+x﹣x=33
6.已知A,B两点都在数轴上,点A所表示的数是a,点B所表示的数是b,并且a=﹣1,AB=3,则( )
A.b=2 B.b=﹣4 C.b=2或b=﹣4 D.b=﹣3
7.如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOE的度数等于( )
A.145° B.135° C.35° D.120°
8.若|x|=7,|y|=5,且x+y>0,那么x﹣y的值是( )
A.2或12 B.2或﹣12 C.﹣2或12 D.﹣2或﹣12
9.如图,下列说法中正确的是( )
A.OA方向是北偏东30° B.OB方向是北偏西75°
C.OC方向是南偏西75° D.OD方向是南偏东45°
10.如图是一个正方体的展开图,把展开图折叠成正方体后,有“弘”字一面的相对面上的字是( )
A.传 B.统 C.文 D.化
二、填空题(每小题3分,共30分)
11.如图,一副三角板(直角顶点重合)摆放在桌面上,若∠AOD=150°,则∠BOC等于 .
13.单项式的系数为m,次数为n,则4mn的值为 .
14.将5.659用四舍五入法精确到0.1,取得的近似值为 .
15.如图,将一个三角板60°角的顶点与另一个三角板的直角顶点重合,∠1=27°40′,则∠2的度数是 .
16.时钟显示的是午后两点半时,时针和分针所夹的角为 .
17.如果a、b互为倒数,c、d互为相反数,且m=1,则代数式2ab﹣(c+d)+m2= .
18.修建公路时,需要将弯曲的道路改直,用数学知识解释为 .
19.多项式x2﹣3kxy﹣3y2+6xy﹣8不含xy项,则k= .
20.如图,由边长相等的黑、白两种颜色的正方形按照一定规律拼接而成,依此规律,第n个图案中白色正方形的个数为 .
三、解答题(共60分)
21.(10分)计算:
(1)﹣62×(﹣)+23÷(﹣);
(2)﹣22×3+(﹣10)÷(﹣2).
22.(5分)先化简,再求值5x2+(4﹣5x﹣3x2)﹣(2x2﹣6x+5),其中x=﹣3.
23.(10分)解方程:
(1)2﹣3(x+1)=1﹣2(1+0.5x);
(2)+1=.
24.(5分)一个角的补角比它的余角的2倍大20°,求这个角的度数.
25.(8分)已知:锐角∠AOB.
(1)若∠AOB=65°,则∠AOB的余角的度数为 度.
(2)若∠AOB=53°17 ,则∠AOB的补角的度数为 .
(3)若∠AOB=31°12 ,计算:∠AOB= .
(4)若∠AOB=20°21 ,计算:3∠AOB.
26.(8分)A,B两地相距150千米,甲车从A地匀速行驶前往B地,每小时行驶40千米;乙车从B地匀速行驶前往A地,每小时行驶60千米.
(1)甲、乙两车同时出发, 小时相遇.
(2)甲、乙两车同时出发, 小时两车相距10千米.
(3)若乙车先行驶半小时,甲车再出发,求甲车出发几小时两车相遇?
27.(6分)如图,线段AB=20,点C是线段AB的中点,点D是线段BC的中点,点E在线段AC上,并且CE=AC.
(1)求线段DB的长.
(2)求线段ED的长.
28.(8分)如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF上的B'处,得到折痕EC,将∠AEF对折,点A落在直线EF上的点A'处,得到折痕EN.
(1)若∠BEC=60°,则∠B'EC= °,∠A'EN= °,∠CEN= °;
(2)若∠BEC=m°,则(1)中∠CEN的值是否改变?∠CEN的度数是多少?请说明你的理由.
2021-2022学年黑龙江省黑河二中七年级(上)期末数学试卷
参考答案与试题解析
一、单项选择题(每小题3分,共30分)
1.﹣2的绝对值是( )
A.2 B.﹣2 C. D.﹣
【分析】根据负数的绝对值等于它的相反数解答.
【解答】解:﹣2的绝对值是2,
即|﹣2|=2.
故选:A.
【点评】本题考查了绝对值的性质:正数的绝对值是它本身;负数的绝对值是它的相反数;0的绝对值是0.
2.下列各数中,比﹣3小的数是( )
A.﹣5 B.﹣1 C.0 D.1
【分析】有理数大小比较的法则:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小,据此判断即可.
【解答】解:﹣5<﹣3<﹣1<0<1,
所以比﹣3小的数是﹣5,
故选:A.
【点评】此题主要考查了有理数大小比较的方法,要熟练掌握,解答此题的关键是要明确:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小.
3.计算:的结果为( )
A.﹣5 B.5 C. D.
【分析】根据有理数的乘除法法则,按照运算顺序,从左往右计算即可.
【解答】解:原式=1×(﹣)
=﹣,
故选:C.
【点评】本题考查了有理数的乘除法法则,掌握同级运算的运算顺序是从左往右是解题的关键.
4.下列各组中,不是同类项的是( )
A.a和﹣a B.3和﹣2 C.3mn和﹣5nm D.﹣x2y和2xy2
【分析】根据同类项的定义(所含字母相同,并且相同字母的指数也相同,这样的项叫做同类项)即可作出判断.
【解答】解:A.a和﹣a所含字母相同,相同字母的指数相同,是同类项,故此选项不符合题意;
B.3和﹣2是同类项,故此选项不符合题意;
C.3mn和﹣5nm所含字母相同,相同字母的指数相同,是同类项,故此选项不符合题意;
D.﹣x2y和2xy2所含字母相同,但相同字母的指数不同,不是同类项,故此选项符合题意.
故选:D.
【点评】本题考查了同类项,掌握同类项的定义是解答本题的关键.
5.古埃及人的“纸草书”中记载了一个数学问题:一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33.若设这个数是x,则所列方程为( )
A.x+x+x=33 B.x+x+x=33
C.x+x+x+x=33 D.x+x+x﹣x=33
【分析】根据题意列方程x+x+x+x=33.
【解答】解:由题意可得x+x+x+x=33.
故选:C.
【点评】本题考查列一元一次方程,解题关键是通过题干找出等量关系.
6.已知A,B两点都在数轴上,点A所表示的数是a,点B所表示的数是b,并且a=﹣1,AB=3,则( )
A.b=2 B.b=﹣4 C.b=2或b=﹣4 D.b=﹣3
【分析】分两种情况:点B在A的左边或右边,列式计算可得答案.
【解答】解:当点B在A的左边时,b=﹣1﹣3=﹣4,
当点B在A的右边时,b=﹣1+3=2;
故选:C.
【点评】本题考查了数轴上两点间的距离,注意分情况讨论是解题关键.
7.如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOE的度数等于( )
A.145° B.135° C.35° D.120°
【分析】根据角平分线的性质可得∠EOA的度数,然后根据补角定义可得答案.
【解答】解:∵OA平分∠EOC,∠EOC=70°,
∴∠EOA=35°,
∴∠BOE=180°﹣35°=145°,
故选:A.
【点评】此题主要考查了角平分线的定义,以及补角定义,关键是掌握角平分线把角分成相等的两部分.
8.若|x|=7,|y|=5,且x+y>0,那么x﹣y的值是( )
A.2或12 B.2或﹣12 C.﹣2或12 D.﹣2或﹣12
【分析】题中给出了x,y的绝对值,可求出x,y的值;再根据x+y>0,分类讨论,求x﹣y的值.
【解答】解:∵|x|=7,|y|=5,
∴x=±7,y=±5.
又x+y>0,则x,y同为正数或x,y异号,但正数的绝对值较大,
∴x=7,y=5或x=7,y=﹣5.
∴x﹣y=2或12.
故选:A.
【点评】理解绝对值的概念,同时要熟练运用有理数的减法运算法则.
9.如图,下列说法中正确的是( )
A.OA方向是北偏东30° B.OB方向是北偏西75°
C.OC方向是南偏西75° D.OD方向是南偏东45°
【分析】根据方向角的概念解答即可.
【解答】解:A、OA方向是北偏东60°,不合题意;
B、OB方向是北偏西15°,不合题意;
C、OC方向是南偏西25°,不合题意;
D、符合题意.
故选:D.
【点评】此题很简单,只要熟知方向角的定义便可解答.
10.如图是一个正方体的展开图,把展开图折叠成正方体后,有“弘”字一面的相对面上的字是( )
A.传 B.统 C.文 D.化
【分析】利用正方体及其表面展开图的特点解题.
【解答】解:这是一个正方体的平面展开图,共有六个面,其中面“扬”与“统”相对,面“弘”与面“文”相对,“传”与面“化”相对.
故选:C.
【点评】本题考查了正方体的展开图得知识,注意正方体的空间图形,从相对面入手,分析及解答问题.
二、填空题(每小题3分,共30分)
11.如图,一副三角板(直角顶点重合)摆放在桌面上,若∠AOD=150°,则∠BOC等于 30° .
【分析】从如图可以看出,∠BOC的度数正好是两直角相加减去∠AOD的度数,从而问题可解.
【解答】解:∵∠AOB=∠COD=90°,∠AOD=150°
∴∠BOC=∠AOB+∠COD﹣∠AOD=90°+90°﹣150°=30°.
故答案为:30°
【点评】此题主要考查学生对角的计算的理解和掌握,解答此题的关键是让学生通过观察图示,发现几个角之间的关系.
13.单项式的系数为m,次数为n,则4mn的值为 .
【分析】根据单项式的系数是数字部分,可得系数m,根据单项式的次数是字母指数和,可得次数n,代入计算可得答案.
【解答】解:∵单项式的系数为m,次数为n,
∴m=﹣,n=1+2=3,
∴4m n=4×(﹣)×3=﹣,
故答案为:﹣.
【点评】本题考查了单项式的定义,确定单项式的系数和次数时,把一个单项式分解成数字因数和字母因式的积,是找准单项式的系数和次数的关键.
14.将5.659用四舍五入法精确到0.1,取得的近似值为 5.7 .
【分析】对百分位数字5四舍五入即可.
【解答】解:将5.659用四舍五入法精确到0.1,取得的近似值为5.7,
故答案为:5.7.
【点评】本题考查了近似数和有效数字:近似数与精确数的接近程度,可以用精确度表示.一般有,精确到哪一位,保留几个有效数字等说法.
15.如图,将一个三角板60°角的顶点与另一个三角板的直角顶点重合,∠1=27°40′,则∠2的度数是 57°40′ .
【分析】根据∠BAC=60°,∠1=27°40′,求出∠EAC的度数,再根据∠2=90°﹣∠EAC,即可求出∠2的度数.
【解答】解:∵∠BAC=60°,∠1=27°40′,
∴∠EAC=60°﹣27°40′=32°20′,
∵∠EAD=90°,
∴∠2=90°﹣∠EAC=90°﹣32°20′=57°40′;
故答案为:57°40′.
【点评】本题主要考查了度分秒的换算,解题的关键是能够正确求出∠EAC的度数.
16.时钟显示的是午后两点半时,时针和分针所夹的角为 105° .
【分析】先分别求出时针和分钟转过的角度,再相减即可.
【解答】解:时针转过的角度是(2+)×30°=75°,
分钟转过的角度是30×6°=180°,
所以钟表在2点半时,其时针和分针所成的角是180°﹣75°=105°,
故答案为:105°.
【点评】本考查了钟面角,能知道时针每小时转30°、分钟每分钟转6°是解此题的关键.
17.如果a、b互为倒数,c、d互为相反数,且m=1,则代数式2ab﹣(c+d)+m2= 3 .
【分析】由题意可知:ab=1,c+d=0,然后代入数值进行计算即可.
【解答】解:∵a、b互为倒数,c、d互为相反数,
∴ab=1,c+d=0.
将ab=1,c+d=0,m=1代入得:原式=2×1﹣0+12=3.
故答案为:3.
【点评】本题主要考查的是求代数式的值,求得ab=1,c+d=0是解题的关键.
18.修建公路时,需要将弯曲的道路改直,用数学知识解释为 两点之间线段最短 .
【分析】根据两点之间线段最短解答.
【解答】解:需要将弯曲的道路改直,用数学知识解释为:两点之间线段最短.
故答案为:两点之间线段最短.
【点评】本题考查了线段的性质,是基础题,熟记两点之间线段最短是解题的关键.
19.多项式x2﹣3kxy﹣3y2+6xy﹣8不含xy项,则k= 2 .
【分析】先将原多项式合并同类项,再令xy项的系数为0,然后解关于k的方程即可求出k.
【解答】解:原式=x2+(﹣3k+6)xy﹣3y2﹣8,
因为不含xy项,
故﹣3k+6=0,
解得:k=2.
故答案为:2.
【点评】本题考查了合并同类项法则及对多项式“项”的概念的理解,题目设计巧妙,有利于培养学生灵活运用知识的能力.
20.如图,由边长相等的黑、白两种颜色的正方形按照一定规律拼接而成,依此规律,第n个图案中白色正方形的个数为 5n+3 .
【分析】根据图形的变化,找出变化规律,再求值即可.
【解答】解:根据题意有,
第1个图案中白色正方形的个数为:3+5×1=8,
第2个图案中白色正方形的个数为:3+5×2=13,
第3个图案中白色正方形的个数为:3+5×3=18,
……,
第n个图案中白色正方形的个数为:3+5×n=5n+3.
故答案为:5n+3.
【点评】本题考查了图形的变化,根据图形的变化找出其规律再求值是解本题的关键,综合性较强,难度适中.
三、解答题(共60分)
21.(10分)计算:
(1)﹣62×(﹣)+23÷(﹣);
(2)﹣22×3+(﹣10)÷(﹣2).
【分析】(1)先算乘方,再算乘除,后算加减,有括号先算括号里,即可解答;
(2)先算乘方,再算乘除,后算加减,即可解答.
【解答】解:(1)﹣62×(﹣)+23÷(﹣)
=﹣36×(﹣)+8×(﹣)
=6+(﹣20)
=﹣14;
(2)﹣22×3+(﹣10)÷(﹣2)
=﹣4×3+5
=﹣12+5
=﹣7.
【点评】本题考查了有理数的混合运算,准确熟练地进行计算是解题的关键.
22.(5分)先化简,再求值5x2+(4﹣5x﹣3x2)﹣(2x2﹣6x+5),其中x=﹣3.
【分析】根据整式的加减法则即可得出答案.
【解答】解:原式=5x2+4﹣5x﹣3x2﹣2x2+6x﹣5
=x﹣1,
当x=﹣3时,
原式=﹣3﹣1=﹣4.
【点评】本题主要考查整式的化简求值,关键是要牢记去括号的法则和合并同类项的原理.
23.(10分)解方程:
(1)2﹣3(x+1)=1﹣2(1+0.5x);
(2)+1=.
【分析】(1)按照解一元一次方程的步骤:去括号,移项,合并同类项,系数化为1,进行计算即可解答;
(2)按照解一元一次方程的步骤:去分母,去括号,移项,合并同类项,系数化为1,进行计算即可解答.
【解答】解:(1)2﹣3(x+1)=1﹣2(1+0.5x),
2﹣3x﹣3=1﹣2﹣x,
﹣3x+x=1﹣2﹣2+3,
﹣2x=0,
x=0;
(2)+1=,
2(2x﹣1)+6=2x+1,
4x﹣2+6=2x+1,
4x﹣2x=1+2﹣6,
2x=﹣3,
x=﹣1.5.
【点评】本题考查了解一元一次方程,熟练掌握解一元一次方程的步骤是解题的关键.
24.(5分)一个角的补角比它的余角的2倍大20°,求这个角的度数.
【分析】设出所求的角为x,则它的补角为180°﹣x,余角为90°﹣x,根据题意列出方程,再解方程即可,
【解答】解:设这个角的度数是x,则它的补角为:180°﹣x,余角为90°﹣x;
由题意,得:(180°﹣x)﹣2(90°﹣x)=20°.
解得:x=20°.
答:这个角的度数是20°.
【点评】本题考查了余角和补角的定义;根据角之间的互余和互补关系列出方程是解决问题的关键.
25.(8分)已知:锐角∠AOB.
(1)若∠AOB=65°,则∠AOB的余角的度数为 25 度.
(2)若∠AOB=53°17 ,则∠AOB的补角的度数为 126°43 .
(3)若∠AOB=31°12 ,计算:∠AOB= 15°36′ .
(4)若∠AOB=20°21 ,计算:3∠AOB.
【分析】(1)根据余角的定义可得结论;
(2)根据补角的定义可得结论;
(3)根据角的倍数关系可得结论;
(4)根据角的倍数关系可得结论.
【解答】解:(1)∠AOB的余角的度数为90°﹣65°=25°;
(2)∠AOB的补角的度数为180°﹣53°17′=126°43 ;
(3)∵∠AOB=31°12 ,
∴∠AOB=×31°12′=×30°72′=15°36′;
(4)∵∠AOB=20°21 ,
∴3∠AOB=3×20°21
=60°63
=61°3 .
【点评】此题考查的是余角和补角的性质,正确计算是关键.
26.(8分)A,B两地相距150千米,甲车从A地匀速行驶前往B地,每小时行驶40千米;乙车从B地匀速行驶前往A地,每小时行驶60千米.
(1)甲、乙两车同时出发, 1.5 小时相遇.
(2)甲、乙两车同时出发, 1.4或1.6 小时两车相距10千米.
(3)若乙车先行驶半小时,甲车再出发,求甲车出发几小时两车相遇?
【分析】(1)设甲、乙两车同时出发,x小时相遇,依据时间=路程÷速度列出方程即可解答,
(1)分两种情况:相遇前两车相距10千米和相遇后两车相距10千米.
(2)设甲车出发y小时后两车相遇,根据A、B两地距离是150米列出方程并解答.
【解答】解:(1)设甲、乙两车同时出发,x小时相遇,
依题意得:(60+40)x=150,
解得x=1.5,
即甲、乙两车同时出发,1.5小时相遇,
故答案为:1.5;
(2)设甲、乙两车同时出发,n小时后两车相距10千米,
①相遇前两车相距10千米,
依题意得:(60+40)n+10=150,
解得n=1.4,
即甲、乙两车同时出发,1.4小时后两车相距10千米;
②相遇后两车相距10千米,
依题意得:(60+40)n﹣10=150,
解得n=1.6
即甲、乙两车同时出发,1.6小时后两车相距10千米;
综上所述,甲、乙两车同时出发,1.4或1.6小时后两车相距10千米,
故答案为:1.4或1.6;
(3)设甲车出发y小时两车相遇,根据题意,得
40y+60y+60×0.5=150.
解得 x=1.2.
∴甲车出发1.2小时两车相遇.
【点评】本题考查了一元一次方程的应用.解答(2)题,要分类讨论,以防漏解.
27.(6分)如图,线段AB=20,点C是线段AB的中点,点D是线段BC的中点,点E在线段AC上,并且CE=AC.
(1)求线段DB的长.
(2)求线段ED的长.
【分析】(1)根据线段中点的性质,可得DC与BC的关系,CE与AC的关系,根据线段的和差,可得答案;
(2)根据线段中点的性质,可得BC的长,可得AC与BC的关系,可得DC的长,根据线段的和差,可得答案.
【解答】解:(1)∵点C是线段AB的中点,
∴AC=BC=×20=10,
∵点D是线段BC的中点,
∴DB=CD=BC=5;
(2)∵CE=AC,
∴CE=×10=4,
∴ED=CE+CD=4+5=9.
【点评】本题考查了两点间的距离,利用线段中点的性质,线段的和差是解题关键.
28.(8分)如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF上的B'处,得到折痕EC,将∠AEF对折,点A落在直线EF上的点A'处,得到折痕EN.
(1)若∠BEC=60°,则∠B'EC= 60 °,∠A'EN= 30 °,∠CEN= 90 °;
(2)若∠BEC=m°,则(1)中∠CEN的值是否改变?∠CEN的度数是多少?请说明你的理由.
【分析】(1)由折叠的性质和∠BEC的度数可得出结论;
(2)解法同(1)过程即可得出结论.
【解答】解:(1)由折叠可知∠BEC=∠B′EC=∠BEB′,∠AEN=∠A′EN=∠AEA′,
∵∠BEC=60°,
∴∠B′EC=60°,
∵∠BEB′+∠AEA′=180°,
∴∠CEN=∠A′EN+∠B′EC=∠BEB′+∠AEA′=90°,
∴∠A′EN=30°,
故答案为:60°,30°,90°.
(2)∠CEN的度数不变,∠CEN=90°,理由如下:
由折叠可知∠BEC=∠B′EC=∠BEB′,∠AEN=∠A′EN=∠AEA′,
∴∠CEN=∠A′EN+∠B′EC=∠BEB′+∠AEA′=90°.
【点评】本题考查了角的计算、折叠的性质以及平行线的性质等知识;熟练掌握对折和平行线的性质是解题的关键.
同课章节目录
