2021-2022学年黑龙江省绥化市绥棱县绥中乡学校八年级(上)期末数学试卷(五四学制)(含解析)
文档属性
| 名称 | 2021-2022学年黑龙江省绥化市绥棱县绥中乡学校八年级(上)期末数学试卷(五四学制)(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 605.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-29 00:00:00 | ||
图片预览




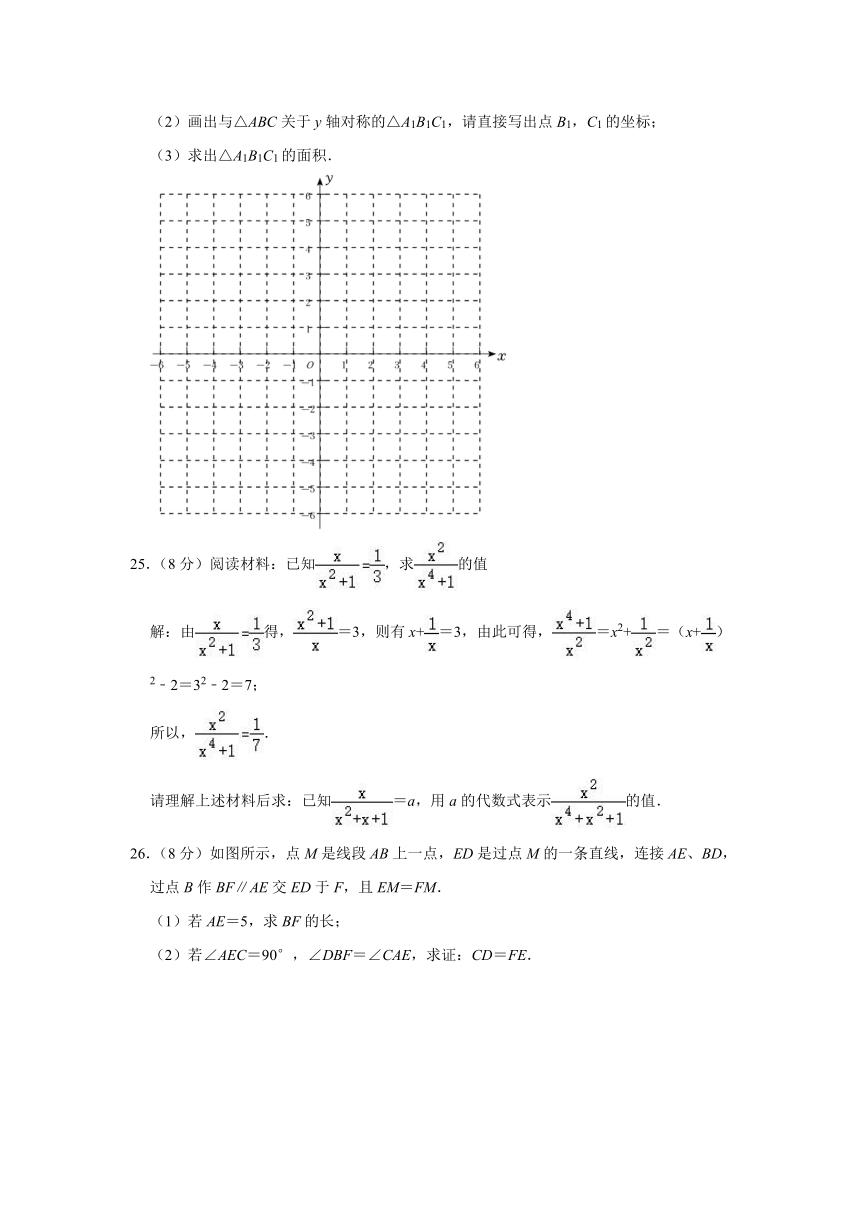
文档简介
2021-2022学年黑龙江省绥化市绥棱县绥中乡学校八年级(上)期末数学试卷(五四学制)
一、单选题(共30分)
1.在下列“禁毒”、“和平”、“志愿者”、“节水”这四个标志中,属于轴对称图形的是( )
A. B.
C. D.
2.下列每组数分别是三根木棒的长度,能用它们摆成三角形的是( )
A.3cm,4cm,8cm B.8cm,7cm,15cm
C.5cm,5cm,11cm D.13cm,12cm,20cm
3.下列计算正确的是( )
A.3x2y+5yx2=8x2y B.2x 3x=6x
C.(3x3)3=9x9 D.(﹣x)3 (﹣3x)=﹣3x4
4.如图,已知∠AOB,用直尺和圆规按照以下步骤作图:①以点O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;②画射线O'A',以点O'为圆心,OC长为半径画弧,交O'A'于点C';③以点C'为圆心,CD长为半径画弧,与第②步中所画的弧相交于点D';④过点D'画射线O'B';根据以上操作,可以判定△OCD≌△O'C'D',其判定的依据是( )
A.AAS B.SAS C.ASA D.SSS
5.下列分式是最简分式的是( )
A. B.
C. D.
6.如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是( )
A.AC=BD B.∠CAB=∠DBA C.∠C=∠D D.BC=AD
7.如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=( )
A.8 B.6 C.5 D.3
8.如图,P是∠BAC平分线上的点,PM⊥AB于M,PN⊥AC于N,则下列结论:
①PM=PN;②AM=AN;③△APM≌△APN;④∠PAN+∠APM=90°.
其中正确结论的个数是( )
A.4个 B.3个 C.2个 D.1个
9.如图,在边长为a的正方形中剪去一个边长为b的小正方形(a>b),把剩下的部分拼成一个梯形,分别计算这两个阴影部分的面积,这个过程验证了公式( )
A.a2﹣b2=(a+b)(a﹣b) B.(a+b)(a﹣b)=a2﹣b2
C.(a+b)2=a2+2ab+b2 D.(a﹣b)2=a2﹣2ab+b2
10.为了让更多的人接种新冠疫苗,某药厂疫苗生产线开足马力,24小时运转,该条生产线计划加工320万支疫苗,前五天按原计划的速度生产,五天后由于原料短缺,以原速度的一半生产,结果比原计划延期3天完成任务.设五天后每天生产x万支疫苗,则可列方程为( )
A. B.
C. D.
二、填空题(共30分)
11.在疫情泛滥期间,口罩已经变成硬通货,其中,N95口罩尤其火爆,N95口罩对直径为0.0000003米(即0.3微米)的颗粒物过滤效果会大于等于95%,0.0000003用科学记数法表示为 .
12.因式分解:(x﹣y)2﹣x+y= .
13.如图,在平面直角坐标系中,已知A(2,0),B(0,3),若在第一象限中找一点C,使得△AOC≌△OAB,则C点的坐标为 .
14.若分式的值为0,则x= .
15.如果10m=12,10n=3,那么10m﹣n= .
16.如图,在正五边形ABCDE中,DF是边CD的延长线,连接BD,则∠BDF的度数是 度.
17.若9a2+Nab+25b2是完全平方式,则N的值为 .
18.将正三角形、正方形、正五边形按照如图所示的位置摆放,如果∠3=33°,那么∠1+
∠2= .
19.如图,已知BD是∠ABC的角平分线,DE⊥AB于E点,AB=8,BC=6,S△ABC=21,则DE= .
20.观察下列各式:;;;;…,则a1+a2+a3+…+a200= .
三、解答题(共60分)
21.(7分)先化简,再求值:,其中a=﹣3.
22.(6分)解分式方程.
23.(6分)如图,△ABC中,∠ACB>∠ABC.
(1)尺规作图:在∠ACB的内部作∠ACD,使∠ACD=∠ABC,射线CD交AB于点D(保留作图痕迹,不写作法);
(2)若∠A=60°,∠B=40°,求∠BDC的度数.
24.(7分)如图,已知在平面直角坐标系中,△ABC的顶点坐标分别为A(1,2),B(3,1),C(4,3).
(1)请在平面直角坐标系中画出△ABC;
(2)画出与△ABC关于y轴对称的△A1B1C1,请直接写出点B1,C1的坐标;
(3)求出△A1B1C1的面积.
25.(8分)阅读材料:已知,求的值
解:由得,=3,则有x+=3,由此可得,=x2+=(x+)2﹣2=32﹣2=7;
所以,.
请理解上述材料后求:已知=a,用a的代数式表示的值.
26.(8分)如图所示,点M是线段AB上一点,ED是过点M的一条直线,连接AE、BD,过点B作BF∥AE交ED于F,且EM=FM.
(1)若AE=5,求BF的长;
(2)若∠AEC=90°,∠DBF=∠CAE,求证:CD=FE.
27.(8分)宇宾服装销售公司准备从广州录辰服装厂购进甲、乙两种服装进行销售,若一件甲种服装的进价比一件乙种服装的进价多50元,用4000元购进甲种服装的数量是用1500元购进乙种服装的数量的2倍.
(1)求每件甲种服装和乙种服装的进价分别是多少元?
(2)该公司甲种服装每件售价260元,乙种服装每件售价190元,公司根据买家需求,决定向这家服装厂购进一批服装,且购进乙种服装的数量比购进甲种服装的数量的2倍还多4件,若本次购进的两种服装全部售出后,总获利不少于7160元,求该公司本次购进甲种服装至少是多少件?
28.(10分)如图,△ABC和△DEC都是等边三角形,D是BC延长线上一点,AD与BE相交于点P,AC、BE相交于点M,AD、CE相交于点N.
求证:
(1)AD=BE;
(2)∠BMC=∠ANC;
(3)△CMN是等边三角形.
2021-2022学年黑龙江省绥化市绥棱县绥中乡学校八年级(上)期末数学试卷(五四学制)
参考答案与试题解析
一、单选题(共30分)
1.在下列“禁毒”、“和平”、“志愿者”、“节水”这四个标志中,属于轴对称图形的是( )
A. B.
C. D.
【分析】根据轴对称图形的概念进行判断即可.
【解答】解:A、不是轴对称图形,故选项错误;
B、是轴对称图形,故选项正确;
C、不是轴对称图形,故选项错误;
D、不是轴对称图形,故选项错误.
故选:B.
2.下列每组数分别是三根木棒的长度,能用它们摆成三角形的是( )
A.3cm,4cm,8cm B.8cm,7cm,15cm
C.5cm,5cm,11cm D.13cm,12cm,20cm
【分析】根据三角形的三边关系,两边之和大于第三边,即两短边的和大于最长的边,即可作出判断.
【解答】解:A、3+4<8,故以这三根木棒不可以构成三角形,不符合题意;
B、8+7=15,故以这三根木棒不能构成三角形,不符合题意;
C、5+5<11,故以这三根木棒不能构成三角形,不符合题意;
D、12+13>20,故以这三根木棒能构成三角形,符合题意.
故选:D.
3.下列计算正确的是( )
A.3x2y+5yx2=8x2y B.2x 3x=6x
C.(3x3)3=9x9 D.(﹣x)3 (﹣3x)=﹣3x4
【分析】根据合并同类项法则、单项式乘单项式的运算法则、积的乘方法则计算,判断即可.
【解答】解:A、3x2y+5yx2=8x2y,本选项计算正确,符合题意;
B、2x 3x=6x2,故本选项计算错误,不符合题意;
C、(3x3)3=27x9,故本选项计算错误,不符合题意;
D、(﹣x)3 (﹣3x)=3x4,故本选项计算错误,不符合题意;
故选:A.
4.如图,已知∠AOB,用直尺和圆规按照以下步骤作图:①以点O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;②画射线O'A',以点O'为圆心,OC长为半径画弧,交O'A'于点C';③以点C'为圆心,CD长为半径画弧,与第②步中所画的弧相交于点D';④过点D'画射线O'B';根据以上操作,可以判定△OCD≌△O'C'D',其判定的依据是( )
A.AAS B.SAS C.ASA D.SSS
【分析】先利用作法得到OD=OC=OD′=OC′,CD=C′D′,然后根据全等三角形的判定方法对各选项进行判断.
【解答】解:由作图得OD=OC=OD′=OC′,CD=C′D′,
则根据“SSS”可判断△C′O′D′≌△COD.
故选:D.
5.下列分式是最简分式的是( )
A. B.
C. D.
【分析】把各个分式化简,只有D不能化简.
【解答】解:∵A:=﹣,
B:=,
C:=﹣,
故选:D.
6.如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是( )
A.AC=BD B.∠CAB=∠DBA C.∠C=∠D D.BC=AD
【分析】根据全等三角形的判定:SAS,AAS,ASA,可得答案.
【解答】解:由题意,得∠ABC=∠BAD,AB=BA,
A、∠ABC=∠BAD,AB=BA,AC=BD,(SSA)三角形不全等,故A错误;
B、在△ABC与△BAD中,,△ABC≌△BAD(ASA),故B正确;
C、在△ABC与△BAD中,,△ABC≌△BAD(AAS),故C正确;
D、在△ABC与△BAD中,,△ABC≌△BAD(SAS),故D正确;
故选:A.
7.如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=( )
A.8 B.6 C.5 D.3
【分析】过点P作PC⊥MN,垂足为C,根据垂直定义可得∠PCO=90°,从而利用直角三角形的两个锐角互余可得∠OPC=30°,然后在Rt△OPC中,利用含30度角的直角三角形的性质可得OC=6,再利用等腰三角形的三线合一性质可得MC=1,最后利用线段的和差关系进行计算即可解答.
【解答】解:过点P作PC⊥MN,垂足为C,
∴∠PCO=90°,
∵∠AOB=60°,
∴∠OPC=90°﹣∠AOB=30°,
∵OP=12,
∴OC=OP=6,
∵PM=PN,PC⊥MN,
∴MC=MN=1,
∴OM=OC﹣MC=6﹣1=5,
故选:C.
8.如图,P是∠BAC平分线上的点,PM⊥AB于M,PN⊥AC于N,则下列结论:
①PM=PN;②AM=AN;③△APM≌△APN;④∠PAN+∠APM=90°.
其中正确结论的个数是( )
A.4个 B.3个 C.2个 D.1个
【分析】由角平分线的性质可判断①;直接利用全等三角形的判定与性质定理可判断②③;利用全等三角形的性质定理可得∠APM=∠APN,由∠PAN+∠APN=90°,等量代换可得结果,可判断④.
【解答】解:∵P是∠BAC平分线上的点,PM⊥AB于M,PN⊥AC于N,
∴PM=PN,故①正确
在Rt△APM和Rt△APN中
,
∴Rt△APM≌Rt△APN(HL),故③正确,
∴AM=AN,故②正确,
∴∠APM=∠APN,
∵∠PAN+∠APN=90°,
∴∠PAN+∠APM=90°,故④正确,
终上所述:正确的有4个.
故选:A.
9.如图,在边长为a的正方形中剪去一个边长为b的小正方形(a>b),把剩下的部分拼成一个梯形,分别计算这两个阴影部分的面积,这个过程验证了公式( )
A.a2﹣b2=(a+b)(a﹣b) B.(a+b)(a﹣b)=a2﹣b2
C.(a+b)2=a2+2ab+b2 D.(a﹣b)2=a2﹣2ab+b2
【分析】用代数式表示左图、右图阴影部分的面积即可.
【解答】解:左图中阴影部分的面积可以看作两个正方形的面积差,即a2﹣b2,
右图中阴影部分是上底为2b,下底为2a,高为a﹣b的梯形,因此面积为(2a+2b)(a﹣b)=(a+b)(a﹣b).
由于左图与右图阴影部分的面积相等,则有a2﹣b2=(a+b)(a﹣b),
故选:A.
10.为了让更多的人接种新冠疫苗,某药厂疫苗生产线开足马力,24小时运转,该条生产线计划加工320万支疫苗,前五天按原计划的速度生产,五天后由于原料短缺,以原速度的一半生产,结果比原计划延期3天完成任务.设五天后每天生产x万支疫苗,则可列方程为( )
A. B.
C. D.
【分析】设五天后每天生产x万支疫苗,则前五天每天生产2x万支疫苗,利用工作时间=工作总量÷工作效率,结合实际比原计划延期3天完成任务,即可得出关于x的分式方程,此题得解.
【解答】解:设五天后每天生产x万支疫苗,则前五天每天生产2x万支疫苗,
依题意得:=﹣3,
即=﹣3.
故选:A.
二、填空题(共30分)
11.在疫情泛滥期间,口罩已经变成硬通货,其中,N95口罩尤其火爆,N95口罩对直径为0.0000003米(即0.3微米)的颗粒物过滤效果会大于等于95%,0.0000003用科学记数法表示为 3×10﹣7 .
【分析】根据用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.即可求解.
【解答】解:0.0000003用科学记数法表示为:3×10﹣7.
故答案为:3×10﹣7.
12.因式分解:(x﹣y)2﹣x+y= (x﹣y)(x﹣y﹣1) .
【分析】首先提取公因式(x﹣y),进而得出答案.
【解答】解:(x﹣y)2﹣x+y
=(x﹣y)2﹣(x﹣y)
=(x﹣y)(x﹣y﹣1).
故答案为:(x﹣y)(x﹣y﹣1).
13.如图,在平面直角坐标系中,已知A(2,0),B(0,3),若在第一象限中找一点C,使得△AOC≌△OAB,则C点的坐标为 (2,3) .
【分析】由题意可知OA为两三角形的公共边,由条件可知△AOC≌△ОAB,再由全等三角形的性质可求得AC=OB,可求得C点坐标.
【解答】解:根据题意C点在第一象限内,且△AOC≌△OAB
如图,
又已知△OAB 和△AOC有已知公共边AO,
∴C(2,3).
故答案为:(2,3).
14.若分式的值为0,则x= ﹣3 .
【分析】根据分式值为零的条件可得:|x|﹣3=0,且(x﹣3)(x+2)≠0,再解即可.
【解答】解:由题意得:|x|﹣3=0,且(x﹣3)(x+2)≠0,
解得:x=﹣3,
故答案为:﹣3.
15.如果10m=12,10n=3,那么10m﹣n= 4 .
【分析】利用同底数幂的除法的法则进行运算即可.
【解答】解:当10m=12,10n=3时,
10m﹣n
=10m÷10n
=12÷3
=4.
故答案为:4.
16.如图,在正五边形ABCDE中,DF是边CD的延长线,连接BD,则∠BDF的度数是 144 度.
【分析】根据正五边形的性质和它的内角和为540°,求得每个内角的度数为108°,再结合等腰三角形和邻补角的定义即可解答.
【解答】解:∵五边形ABCDE是正五边形,
∴∠C==108°,BC=DC,
∴∠BDC=∠DBC=(180°﹣∠C)=(180°﹣108°)=36°,
∴∠BDF=180°﹣∠BDC=180°﹣36°=144°,
故答案为:144.
17.若9a2+Nab+25b2是完全平方式,则N的值为 ±30. .
【分析】先根据两平方项确定出这两个数,再根据完全平方公式的乘积二倍项即可确定N的值.
【解答】解:∵9a2+Nab+25b2是完全平方式,
∴N=±2×3×5,
解得m=±30.
故答案为:±30.
18.将正三角形、正方形、正五边形按照如图所示的位置摆放,如果∠3=33°,那么∠1+
∠2= 69° .
【分析】分别根据正三角形、正四边形、正五边形各内角的度数及平角的定义进行解答即可.
【解答】解:∵∠3=33°,正三角形的内角是60°,正四边形的内角是90°,正五边形的内角是108°,
∴∠4=180°﹣60°﹣33°=87°,
∴∠5+∠6=180°﹣87°=93°,
∵∠5=180°﹣∠2﹣108°=72°﹣∠2 ①,
∠6=180°﹣90°﹣∠1=90°﹣∠1 ②,
∴①+②得,180°﹣∠2﹣108°+90°﹣∠1=93°,
即∠1+∠2=69°.
故答案为:69°.
19.如图,已知BD是∠ABC的角平分线,DE⊥AB于E点,AB=8,BC=6,S△ABC=21,则DE= 3 .
【分析】过D作DF⊥BC于F,根据角平分线性质求出DE=DF,根据三角形的面积公式得出关于DE的方程,求出方程的解即可.
【解答】解:过D作DF⊥BC于F,
∵BD是∠ABC的角平分线,DE⊥AB,
∴DF=DE,
∵S△ABC=21,AB=8,BC=6,
∴×BC×DF+×AB×DE=21,
∴×6×DE+×8×DE=21,
∴DE=3,
故答案为:3.
20.观察下列各式:;;;;…,则a1+a2+a3+…+a200= .
【分析】直接利用已知算式得出规律,进而化简得出答案.
【解答】解:原式=(1﹣)+(﹣)+(﹣)+...+(﹣)
=(1﹣+﹣+﹣+...+﹣)
=×(1﹣)
=.
故答案为:.
三、解答题(共60分)
21.(7分)先化简,再求值:,其中a=﹣3.
【分析】根据分式的混合运算法则把原式化简,把a的值代入计算即可.
【解答】解:原式=(﹣)
=
=,
当a=﹣3时,原式==.
22.(6分)解分式方程.
【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
【解答】解:去分母得:x2﹣x(x﹣1)=3,
解得:x=3,
检验:当x=3时,x(x﹣1)=6≠0,
∴分式方程的解为x=3.
23.(6分)如图,△ABC中,∠ACB>∠ABC.
(1)尺规作图:在∠ACB的内部作∠ACD,使∠ACD=∠ABC,射线CD交AB于点D(保留作图痕迹,不写作法);
(2)若∠A=60°,∠B=40°,求∠BDC的度数.
【分析】(1)利用基本作图,作∠ACD=∠B即可;
(2)先利用三角形内角和计算出∠ACB的度数,再根据角平分线的定义得到∠ACD的度数,然后根据三角形外角性质计算∠BDC的度数.
【解答】解:(1)如图,∠ACD为所作;
(2)∵∠A=60°,∠B=40°,
∴∠ACB=180°﹣∠A﹣∠B=80°,
∵CD平分∠ACB,
∴∠ACD=∠ACB=40°,
∴∠BDC=∠A+∠ACD=60°+40°=100°.
24.(7分)如图,已知在平面直角坐标系中,△ABC的顶点坐标分别为A(1,2),B(3,1),C(4,3).
(1)请在平面直角坐标系中画出△ABC;
(2)画出与△ABC关于y轴对称的△A1B1C1,请直接写出点B1,C1的坐标;
(3)求出△A1B1C1的面积.
【分析】(1)描点、连线即可;
(2)分别作出三个顶点关于y轴的对称点,再首尾顺次连接即可;
(3)用矩形的面积减去四周三个三角形的面积即可.
【解答】解:(1)如图所示即为所求图形.
(2)△A1B1C1即为所求图形,B1(﹣3,1),C1(﹣4,3);
(3).
25.(8分)阅读材料:已知,求的值
解:由得,=3,则有x+=3,由此可得,=x2+=(x+)2﹣2=32﹣2=7;
所以,.
请理解上述材料后求:已知=a,用a的代数式表示的值.
【分析】由=a,可得=,进而得到x+=﹣1,再根据=x2++1=﹣2+1=﹣1,整体代入即可得到的值.
【解答】解:由=a,可得=,
则有x+=﹣1,
由此可得,=x2++1=﹣2+1=﹣1=﹣1=,
所以,=.
26.(8分)如图所示,点M是线段AB上一点,ED是过点M的一条直线,连接AE、BD,过点B作BF∥AE交ED于F,且EM=FM.
(1)若AE=5,求BF的长;
(2)若∠AEC=90°,∠DBF=∠CAE,求证:CD=FE.
【分析】(1)根据平行线的性质得到∠EAM=∠FBM,∠E=∠BFM,即可利用AAS证明△AEM≌△BFM,再根据全等三角形的性质即可得解;
(2)根据平行线的性质得出∠BFM=90°,再根据平角的定义得到∠BFD=90°,进而得出∠AEC=∠BFD,即可利用ASA证明△ACE≌△BDF,根据全等三角形的性质得到CE=DF,再根据线段的和差即可得解.
【解答】(1)解:∵BF∥AE,
∴∠EAM=∠FBM,∠E=∠BFM,
在△AEM和△BFM中,
,
∴△AEM≌△BFM(AAS),
∴AE=BF,
∵AE=5,
∴BF=5;
(2)证明:∵BF∥AE,
∴∠AEC=∠BFM,
∵∠AEC=90°,
∴∠BFM=90°,
∴∠BFD=180°﹣90°=90°,
∴∠AEC=∠BFD,
由(1)知AE=BF,
在△ACE和△BDF中,
,
∴△ACE≌△BDF(ASA),
∴CE=DF,
∴DF﹣CF=CE﹣CF,
即CD=FE.
27.(8分)宇宾服装销售公司准备从广州录辰服装厂购进甲、乙两种服装进行销售,若一件甲种服装的进价比一件乙种服装的进价多50元,用4000元购进甲种服装的数量是用1500元购进乙种服装的数量的2倍.
(1)求每件甲种服装和乙种服装的进价分别是多少元?
(2)该公司甲种服装每件售价260元,乙种服装每件售价190元,公司根据买家需求,决定向这家服装厂购进一批服装,且购进乙种服装的数量比购进甲种服装的数量的2倍还多4件,若本次购进的两种服装全部售出后,总获利不少于7160元,求该公司本次购进甲种服装至少是多少件?
【分析】(1)设每件甲种服装为x元,每件乙种服装为(x﹣50)元,根据关键语句“用4000元购进甲种服装的数量是用1500元购进乙种服装的数量的2倍”可列方程求解;
(2)设购进甲种服装m件,则购进乙种服装(2m+4)件,根据题意可得不等关系:甲服装的利润+乙服装的利润≥7160元,根据不等关系列出不等式,解出解集,即可确定答案.
【解答】解:(1)设每件甲种服装为x元,每件乙种服装为(x﹣50)元,
由题意得:=×2,
解得:x=200,
经检验x=200是原分式方程的解,
则:x﹣50=200﹣50=150.
答:每件甲种服装为200元,每件乙种服装为150元;
(2)设购进甲种服装m件,则购进乙种服装(2m+4)件,由题意得:
(260﹣200)m+(190﹣150)(2m+4)≥7160,
解得:m≥50.
答:该公司本次购进甲种服装至少是50件.
28.(10分)如图,△ABC和△DEC都是等边三角形,D是BC延长线上一点,AD与BE相交于点P,AC、BE相交于点M,AD、CE相交于点N.
求证:
(1)AD=BE;
(2)∠BMC=∠ANC;
(3)△CMN是等边三角形.
【分析】(1)根据证明△BCE≌△ACD,得出AD=BE;
(2)根据全等三角形的性质解答即可;
(3)由△ACN≌△BCM得到CN=BM,加上∠MCN=60°,则根据等边三角形的判定即可得到△CMN为等边三角形.
【解答】证明:(1)∵△ABC和△DEC都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠ECD=60°,
∴∠ACB+∠ACE=∠ECD+∠ACE,
即∠BCE=∠ACD,
在△BCE与△ACD中,
,
∴△BCE≌△ACD(SAS),
∴AD=BE;
(2)∵∠ACB=∠ACE=60°,
由△BCE≌△ACD得:∠CBE=∠CAD,
∴∠BMC=∠ANC;
(3)∵△ACD≌△BCE,
∴∠CAD=∠CBE,
在△ACN和△BCM中,
,
∴△ACN≌△BCM(ASA),
∴CM=CN,
∴△CMN为等腰三角形,
∵∠MCN=60°,
∴△CMN是等边三角形.
一、单选题(共30分)
1.在下列“禁毒”、“和平”、“志愿者”、“节水”这四个标志中,属于轴对称图形的是( )
A. B.
C. D.
2.下列每组数分别是三根木棒的长度,能用它们摆成三角形的是( )
A.3cm,4cm,8cm B.8cm,7cm,15cm
C.5cm,5cm,11cm D.13cm,12cm,20cm
3.下列计算正确的是( )
A.3x2y+5yx2=8x2y B.2x 3x=6x
C.(3x3)3=9x9 D.(﹣x)3 (﹣3x)=﹣3x4
4.如图,已知∠AOB,用直尺和圆规按照以下步骤作图:①以点O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;②画射线O'A',以点O'为圆心,OC长为半径画弧,交O'A'于点C';③以点C'为圆心,CD长为半径画弧,与第②步中所画的弧相交于点D';④过点D'画射线O'B';根据以上操作,可以判定△OCD≌△O'C'D',其判定的依据是( )
A.AAS B.SAS C.ASA D.SSS
5.下列分式是最简分式的是( )
A. B.
C. D.
6.如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是( )
A.AC=BD B.∠CAB=∠DBA C.∠C=∠D D.BC=AD
7.如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=( )
A.8 B.6 C.5 D.3
8.如图,P是∠BAC平分线上的点,PM⊥AB于M,PN⊥AC于N,则下列结论:
①PM=PN;②AM=AN;③△APM≌△APN;④∠PAN+∠APM=90°.
其中正确结论的个数是( )
A.4个 B.3个 C.2个 D.1个
9.如图,在边长为a的正方形中剪去一个边长为b的小正方形(a>b),把剩下的部分拼成一个梯形,分别计算这两个阴影部分的面积,这个过程验证了公式( )
A.a2﹣b2=(a+b)(a﹣b) B.(a+b)(a﹣b)=a2﹣b2
C.(a+b)2=a2+2ab+b2 D.(a﹣b)2=a2﹣2ab+b2
10.为了让更多的人接种新冠疫苗,某药厂疫苗生产线开足马力,24小时运转,该条生产线计划加工320万支疫苗,前五天按原计划的速度生产,五天后由于原料短缺,以原速度的一半生产,结果比原计划延期3天完成任务.设五天后每天生产x万支疫苗,则可列方程为( )
A. B.
C. D.
二、填空题(共30分)
11.在疫情泛滥期间,口罩已经变成硬通货,其中,N95口罩尤其火爆,N95口罩对直径为0.0000003米(即0.3微米)的颗粒物过滤效果会大于等于95%,0.0000003用科学记数法表示为 .
12.因式分解:(x﹣y)2﹣x+y= .
13.如图,在平面直角坐标系中,已知A(2,0),B(0,3),若在第一象限中找一点C,使得△AOC≌△OAB,则C点的坐标为 .
14.若分式的值为0,则x= .
15.如果10m=12,10n=3,那么10m﹣n= .
16.如图,在正五边形ABCDE中,DF是边CD的延长线,连接BD,则∠BDF的度数是 度.
17.若9a2+Nab+25b2是完全平方式,则N的值为 .
18.将正三角形、正方形、正五边形按照如图所示的位置摆放,如果∠3=33°,那么∠1+
∠2= .
19.如图,已知BD是∠ABC的角平分线,DE⊥AB于E点,AB=8,BC=6,S△ABC=21,则DE= .
20.观察下列各式:;;;;…,则a1+a2+a3+…+a200= .
三、解答题(共60分)
21.(7分)先化简,再求值:,其中a=﹣3.
22.(6分)解分式方程.
23.(6分)如图,△ABC中,∠ACB>∠ABC.
(1)尺规作图:在∠ACB的内部作∠ACD,使∠ACD=∠ABC,射线CD交AB于点D(保留作图痕迹,不写作法);
(2)若∠A=60°,∠B=40°,求∠BDC的度数.
24.(7分)如图,已知在平面直角坐标系中,△ABC的顶点坐标分别为A(1,2),B(3,1),C(4,3).
(1)请在平面直角坐标系中画出△ABC;
(2)画出与△ABC关于y轴对称的△A1B1C1,请直接写出点B1,C1的坐标;
(3)求出△A1B1C1的面积.
25.(8分)阅读材料:已知,求的值
解:由得,=3,则有x+=3,由此可得,=x2+=(x+)2﹣2=32﹣2=7;
所以,.
请理解上述材料后求:已知=a,用a的代数式表示的值.
26.(8分)如图所示,点M是线段AB上一点,ED是过点M的一条直线,连接AE、BD,过点B作BF∥AE交ED于F,且EM=FM.
(1)若AE=5,求BF的长;
(2)若∠AEC=90°,∠DBF=∠CAE,求证:CD=FE.
27.(8分)宇宾服装销售公司准备从广州录辰服装厂购进甲、乙两种服装进行销售,若一件甲种服装的进价比一件乙种服装的进价多50元,用4000元购进甲种服装的数量是用1500元购进乙种服装的数量的2倍.
(1)求每件甲种服装和乙种服装的进价分别是多少元?
(2)该公司甲种服装每件售价260元,乙种服装每件售价190元,公司根据买家需求,决定向这家服装厂购进一批服装,且购进乙种服装的数量比购进甲种服装的数量的2倍还多4件,若本次购进的两种服装全部售出后,总获利不少于7160元,求该公司本次购进甲种服装至少是多少件?
28.(10分)如图,△ABC和△DEC都是等边三角形,D是BC延长线上一点,AD与BE相交于点P,AC、BE相交于点M,AD、CE相交于点N.
求证:
(1)AD=BE;
(2)∠BMC=∠ANC;
(3)△CMN是等边三角形.
2021-2022学年黑龙江省绥化市绥棱县绥中乡学校八年级(上)期末数学试卷(五四学制)
参考答案与试题解析
一、单选题(共30分)
1.在下列“禁毒”、“和平”、“志愿者”、“节水”这四个标志中,属于轴对称图形的是( )
A. B.
C. D.
【分析】根据轴对称图形的概念进行判断即可.
【解答】解:A、不是轴对称图形,故选项错误;
B、是轴对称图形,故选项正确;
C、不是轴对称图形,故选项错误;
D、不是轴对称图形,故选项错误.
故选:B.
2.下列每组数分别是三根木棒的长度,能用它们摆成三角形的是( )
A.3cm,4cm,8cm B.8cm,7cm,15cm
C.5cm,5cm,11cm D.13cm,12cm,20cm
【分析】根据三角形的三边关系,两边之和大于第三边,即两短边的和大于最长的边,即可作出判断.
【解答】解:A、3+4<8,故以这三根木棒不可以构成三角形,不符合题意;
B、8+7=15,故以这三根木棒不能构成三角形,不符合题意;
C、5+5<11,故以这三根木棒不能构成三角形,不符合题意;
D、12+13>20,故以这三根木棒能构成三角形,符合题意.
故选:D.
3.下列计算正确的是( )
A.3x2y+5yx2=8x2y B.2x 3x=6x
C.(3x3)3=9x9 D.(﹣x)3 (﹣3x)=﹣3x4
【分析】根据合并同类项法则、单项式乘单项式的运算法则、积的乘方法则计算,判断即可.
【解答】解:A、3x2y+5yx2=8x2y,本选项计算正确,符合题意;
B、2x 3x=6x2,故本选项计算错误,不符合题意;
C、(3x3)3=27x9,故本选项计算错误,不符合题意;
D、(﹣x)3 (﹣3x)=3x4,故本选项计算错误,不符合题意;
故选:A.
4.如图,已知∠AOB,用直尺和圆规按照以下步骤作图:①以点O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;②画射线O'A',以点O'为圆心,OC长为半径画弧,交O'A'于点C';③以点C'为圆心,CD长为半径画弧,与第②步中所画的弧相交于点D';④过点D'画射线O'B';根据以上操作,可以判定△OCD≌△O'C'D',其判定的依据是( )
A.AAS B.SAS C.ASA D.SSS
【分析】先利用作法得到OD=OC=OD′=OC′,CD=C′D′,然后根据全等三角形的判定方法对各选项进行判断.
【解答】解:由作图得OD=OC=OD′=OC′,CD=C′D′,
则根据“SSS”可判断△C′O′D′≌△COD.
故选:D.
5.下列分式是最简分式的是( )
A. B.
C. D.
【分析】把各个分式化简,只有D不能化简.
【解答】解:∵A:=﹣,
B:=,
C:=﹣,
故选:D.
6.如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是( )
A.AC=BD B.∠CAB=∠DBA C.∠C=∠D D.BC=AD
【分析】根据全等三角形的判定:SAS,AAS,ASA,可得答案.
【解答】解:由题意,得∠ABC=∠BAD,AB=BA,
A、∠ABC=∠BAD,AB=BA,AC=BD,(SSA)三角形不全等,故A错误;
B、在△ABC与△BAD中,,△ABC≌△BAD(ASA),故B正确;
C、在△ABC与△BAD中,,△ABC≌△BAD(AAS),故C正确;
D、在△ABC与△BAD中,,△ABC≌△BAD(SAS),故D正确;
故选:A.
7.如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=( )
A.8 B.6 C.5 D.3
【分析】过点P作PC⊥MN,垂足为C,根据垂直定义可得∠PCO=90°,从而利用直角三角形的两个锐角互余可得∠OPC=30°,然后在Rt△OPC中,利用含30度角的直角三角形的性质可得OC=6,再利用等腰三角形的三线合一性质可得MC=1,最后利用线段的和差关系进行计算即可解答.
【解答】解:过点P作PC⊥MN,垂足为C,
∴∠PCO=90°,
∵∠AOB=60°,
∴∠OPC=90°﹣∠AOB=30°,
∵OP=12,
∴OC=OP=6,
∵PM=PN,PC⊥MN,
∴MC=MN=1,
∴OM=OC﹣MC=6﹣1=5,
故选:C.
8.如图,P是∠BAC平分线上的点,PM⊥AB于M,PN⊥AC于N,则下列结论:
①PM=PN;②AM=AN;③△APM≌△APN;④∠PAN+∠APM=90°.
其中正确结论的个数是( )
A.4个 B.3个 C.2个 D.1个
【分析】由角平分线的性质可判断①;直接利用全等三角形的判定与性质定理可判断②③;利用全等三角形的性质定理可得∠APM=∠APN,由∠PAN+∠APN=90°,等量代换可得结果,可判断④.
【解答】解:∵P是∠BAC平分线上的点,PM⊥AB于M,PN⊥AC于N,
∴PM=PN,故①正确
在Rt△APM和Rt△APN中
,
∴Rt△APM≌Rt△APN(HL),故③正确,
∴AM=AN,故②正确,
∴∠APM=∠APN,
∵∠PAN+∠APN=90°,
∴∠PAN+∠APM=90°,故④正确,
终上所述:正确的有4个.
故选:A.
9.如图,在边长为a的正方形中剪去一个边长为b的小正方形(a>b),把剩下的部分拼成一个梯形,分别计算这两个阴影部分的面积,这个过程验证了公式( )
A.a2﹣b2=(a+b)(a﹣b) B.(a+b)(a﹣b)=a2﹣b2
C.(a+b)2=a2+2ab+b2 D.(a﹣b)2=a2﹣2ab+b2
【分析】用代数式表示左图、右图阴影部分的面积即可.
【解答】解:左图中阴影部分的面积可以看作两个正方形的面积差,即a2﹣b2,
右图中阴影部分是上底为2b,下底为2a,高为a﹣b的梯形,因此面积为(2a+2b)(a﹣b)=(a+b)(a﹣b).
由于左图与右图阴影部分的面积相等,则有a2﹣b2=(a+b)(a﹣b),
故选:A.
10.为了让更多的人接种新冠疫苗,某药厂疫苗生产线开足马力,24小时运转,该条生产线计划加工320万支疫苗,前五天按原计划的速度生产,五天后由于原料短缺,以原速度的一半生产,结果比原计划延期3天完成任务.设五天后每天生产x万支疫苗,则可列方程为( )
A. B.
C. D.
【分析】设五天后每天生产x万支疫苗,则前五天每天生产2x万支疫苗,利用工作时间=工作总量÷工作效率,结合实际比原计划延期3天完成任务,即可得出关于x的分式方程,此题得解.
【解答】解:设五天后每天生产x万支疫苗,则前五天每天生产2x万支疫苗,
依题意得:=﹣3,
即=﹣3.
故选:A.
二、填空题(共30分)
11.在疫情泛滥期间,口罩已经变成硬通货,其中,N95口罩尤其火爆,N95口罩对直径为0.0000003米(即0.3微米)的颗粒物过滤效果会大于等于95%,0.0000003用科学记数法表示为 3×10﹣7 .
【分析】根据用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.即可求解.
【解答】解:0.0000003用科学记数法表示为:3×10﹣7.
故答案为:3×10﹣7.
12.因式分解:(x﹣y)2﹣x+y= (x﹣y)(x﹣y﹣1) .
【分析】首先提取公因式(x﹣y),进而得出答案.
【解答】解:(x﹣y)2﹣x+y
=(x﹣y)2﹣(x﹣y)
=(x﹣y)(x﹣y﹣1).
故答案为:(x﹣y)(x﹣y﹣1).
13.如图,在平面直角坐标系中,已知A(2,0),B(0,3),若在第一象限中找一点C,使得△AOC≌△OAB,则C点的坐标为 (2,3) .
【分析】由题意可知OA为两三角形的公共边,由条件可知△AOC≌△ОAB,再由全等三角形的性质可求得AC=OB,可求得C点坐标.
【解答】解:根据题意C点在第一象限内,且△AOC≌△OAB
如图,
又已知△OAB 和△AOC有已知公共边AO,
∴C(2,3).
故答案为:(2,3).
14.若分式的值为0,则x= ﹣3 .
【分析】根据分式值为零的条件可得:|x|﹣3=0,且(x﹣3)(x+2)≠0,再解即可.
【解答】解:由题意得:|x|﹣3=0,且(x﹣3)(x+2)≠0,
解得:x=﹣3,
故答案为:﹣3.
15.如果10m=12,10n=3,那么10m﹣n= 4 .
【分析】利用同底数幂的除法的法则进行运算即可.
【解答】解:当10m=12,10n=3时,
10m﹣n
=10m÷10n
=12÷3
=4.
故答案为:4.
16.如图,在正五边形ABCDE中,DF是边CD的延长线,连接BD,则∠BDF的度数是 144 度.
【分析】根据正五边形的性质和它的内角和为540°,求得每个内角的度数为108°,再结合等腰三角形和邻补角的定义即可解答.
【解答】解:∵五边形ABCDE是正五边形,
∴∠C==108°,BC=DC,
∴∠BDC=∠DBC=(180°﹣∠C)=(180°﹣108°)=36°,
∴∠BDF=180°﹣∠BDC=180°﹣36°=144°,
故答案为:144.
17.若9a2+Nab+25b2是完全平方式,则N的值为 ±30. .
【分析】先根据两平方项确定出这两个数,再根据完全平方公式的乘积二倍项即可确定N的值.
【解答】解:∵9a2+Nab+25b2是完全平方式,
∴N=±2×3×5,
解得m=±30.
故答案为:±30.
18.将正三角形、正方形、正五边形按照如图所示的位置摆放,如果∠3=33°,那么∠1+
∠2= 69° .
【分析】分别根据正三角形、正四边形、正五边形各内角的度数及平角的定义进行解答即可.
【解答】解:∵∠3=33°,正三角形的内角是60°,正四边形的内角是90°,正五边形的内角是108°,
∴∠4=180°﹣60°﹣33°=87°,
∴∠5+∠6=180°﹣87°=93°,
∵∠5=180°﹣∠2﹣108°=72°﹣∠2 ①,
∠6=180°﹣90°﹣∠1=90°﹣∠1 ②,
∴①+②得,180°﹣∠2﹣108°+90°﹣∠1=93°,
即∠1+∠2=69°.
故答案为:69°.
19.如图,已知BD是∠ABC的角平分线,DE⊥AB于E点,AB=8,BC=6,S△ABC=21,则DE= 3 .
【分析】过D作DF⊥BC于F,根据角平分线性质求出DE=DF,根据三角形的面积公式得出关于DE的方程,求出方程的解即可.
【解答】解:过D作DF⊥BC于F,
∵BD是∠ABC的角平分线,DE⊥AB,
∴DF=DE,
∵S△ABC=21,AB=8,BC=6,
∴×BC×DF+×AB×DE=21,
∴×6×DE+×8×DE=21,
∴DE=3,
故答案为:3.
20.观察下列各式:;;;;…,则a1+a2+a3+…+a200= .
【分析】直接利用已知算式得出规律,进而化简得出答案.
【解答】解:原式=(1﹣)+(﹣)+(﹣)+...+(﹣)
=(1﹣+﹣+﹣+...+﹣)
=×(1﹣)
=.
故答案为:.
三、解答题(共60分)
21.(7分)先化简,再求值:,其中a=﹣3.
【分析】根据分式的混合运算法则把原式化简,把a的值代入计算即可.
【解答】解:原式=(﹣)
=
=,
当a=﹣3时,原式==.
22.(6分)解分式方程.
【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
【解答】解:去分母得:x2﹣x(x﹣1)=3,
解得:x=3,
检验:当x=3时,x(x﹣1)=6≠0,
∴分式方程的解为x=3.
23.(6分)如图,△ABC中,∠ACB>∠ABC.
(1)尺规作图:在∠ACB的内部作∠ACD,使∠ACD=∠ABC,射线CD交AB于点D(保留作图痕迹,不写作法);
(2)若∠A=60°,∠B=40°,求∠BDC的度数.
【分析】(1)利用基本作图,作∠ACD=∠B即可;
(2)先利用三角形内角和计算出∠ACB的度数,再根据角平分线的定义得到∠ACD的度数,然后根据三角形外角性质计算∠BDC的度数.
【解答】解:(1)如图,∠ACD为所作;
(2)∵∠A=60°,∠B=40°,
∴∠ACB=180°﹣∠A﹣∠B=80°,
∵CD平分∠ACB,
∴∠ACD=∠ACB=40°,
∴∠BDC=∠A+∠ACD=60°+40°=100°.
24.(7分)如图,已知在平面直角坐标系中,△ABC的顶点坐标分别为A(1,2),B(3,1),C(4,3).
(1)请在平面直角坐标系中画出△ABC;
(2)画出与△ABC关于y轴对称的△A1B1C1,请直接写出点B1,C1的坐标;
(3)求出△A1B1C1的面积.
【分析】(1)描点、连线即可;
(2)分别作出三个顶点关于y轴的对称点,再首尾顺次连接即可;
(3)用矩形的面积减去四周三个三角形的面积即可.
【解答】解:(1)如图所示即为所求图形.
(2)△A1B1C1即为所求图形,B1(﹣3,1),C1(﹣4,3);
(3).
25.(8分)阅读材料:已知,求的值
解:由得,=3,则有x+=3,由此可得,=x2+=(x+)2﹣2=32﹣2=7;
所以,.
请理解上述材料后求:已知=a,用a的代数式表示的值.
【分析】由=a,可得=,进而得到x+=﹣1,再根据=x2++1=﹣2+1=﹣1,整体代入即可得到的值.
【解答】解:由=a,可得=,
则有x+=﹣1,
由此可得,=x2++1=﹣2+1=﹣1=﹣1=,
所以,=.
26.(8分)如图所示,点M是线段AB上一点,ED是过点M的一条直线,连接AE、BD,过点B作BF∥AE交ED于F,且EM=FM.
(1)若AE=5,求BF的长;
(2)若∠AEC=90°,∠DBF=∠CAE,求证:CD=FE.
【分析】(1)根据平行线的性质得到∠EAM=∠FBM,∠E=∠BFM,即可利用AAS证明△AEM≌△BFM,再根据全等三角形的性质即可得解;
(2)根据平行线的性质得出∠BFM=90°,再根据平角的定义得到∠BFD=90°,进而得出∠AEC=∠BFD,即可利用ASA证明△ACE≌△BDF,根据全等三角形的性质得到CE=DF,再根据线段的和差即可得解.
【解答】(1)解:∵BF∥AE,
∴∠EAM=∠FBM,∠E=∠BFM,
在△AEM和△BFM中,
,
∴△AEM≌△BFM(AAS),
∴AE=BF,
∵AE=5,
∴BF=5;
(2)证明:∵BF∥AE,
∴∠AEC=∠BFM,
∵∠AEC=90°,
∴∠BFM=90°,
∴∠BFD=180°﹣90°=90°,
∴∠AEC=∠BFD,
由(1)知AE=BF,
在△ACE和△BDF中,
,
∴△ACE≌△BDF(ASA),
∴CE=DF,
∴DF﹣CF=CE﹣CF,
即CD=FE.
27.(8分)宇宾服装销售公司准备从广州录辰服装厂购进甲、乙两种服装进行销售,若一件甲种服装的进价比一件乙种服装的进价多50元,用4000元购进甲种服装的数量是用1500元购进乙种服装的数量的2倍.
(1)求每件甲种服装和乙种服装的进价分别是多少元?
(2)该公司甲种服装每件售价260元,乙种服装每件售价190元,公司根据买家需求,决定向这家服装厂购进一批服装,且购进乙种服装的数量比购进甲种服装的数量的2倍还多4件,若本次购进的两种服装全部售出后,总获利不少于7160元,求该公司本次购进甲种服装至少是多少件?
【分析】(1)设每件甲种服装为x元,每件乙种服装为(x﹣50)元,根据关键语句“用4000元购进甲种服装的数量是用1500元购进乙种服装的数量的2倍”可列方程求解;
(2)设购进甲种服装m件,则购进乙种服装(2m+4)件,根据题意可得不等关系:甲服装的利润+乙服装的利润≥7160元,根据不等关系列出不等式,解出解集,即可确定答案.
【解答】解:(1)设每件甲种服装为x元,每件乙种服装为(x﹣50)元,
由题意得:=×2,
解得:x=200,
经检验x=200是原分式方程的解,
则:x﹣50=200﹣50=150.
答:每件甲种服装为200元,每件乙种服装为150元;
(2)设购进甲种服装m件,则购进乙种服装(2m+4)件,由题意得:
(260﹣200)m+(190﹣150)(2m+4)≥7160,
解得:m≥50.
答:该公司本次购进甲种服装至少是50件.
28.(10分)如图,△ABC和△DEC都是等边三角形,D是BC延长线上一点,AD与BE相交于点P,AC、BE相交于点M,AD、CE相交于点N.
求证:
(1)AD=BE;
(2)∠BMC=∠ANC;
(3)△CMN是等边三角形.
【分析】(1)根据证明△BCE≌△ACD,得出AD=BE;
(2)根据全等三角形的性质解答即可;
(3)由△ACN≌△BCM得到CN=BM,加上∠MCN=60°,则根据等边三角形的判定即可得到△CMN为等边三角形.
【解答】证明:(1)∵△ABC和△DEC都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠ECD=60°,
∴∠ACB+∠ACE=∠ECD+∠ACE,
即∠BCE=∠ACD,
在△BCE与△ACD中,
,
∴△BCE≌△ACD(SAS),
∴AD=BE;
(2)∵∠ACB=∠ACE=60°,
由△BCE≌△ACD得:∠CBE=∠CAD,
∴∠BMC=∠ANC;
(3)∵△ACD≌△BCE,
∴∠CAD=∠CBE,
在△ACN和△BCM中,
,
∴△ACN≌△BCM(ASA),
∴CM=CN,
∴△CMN为等腰三角形,
∵∠MCN=60°,
∴△CMN是等边三角形.
同课章节目录
