苏科版9年级数学下册5.5 用二次函数解决问题课时练(含答案)
文档属性
| 名称 | 苏科版9年级数学下册5.5 用二次函数解决问题课时练(含答案) | 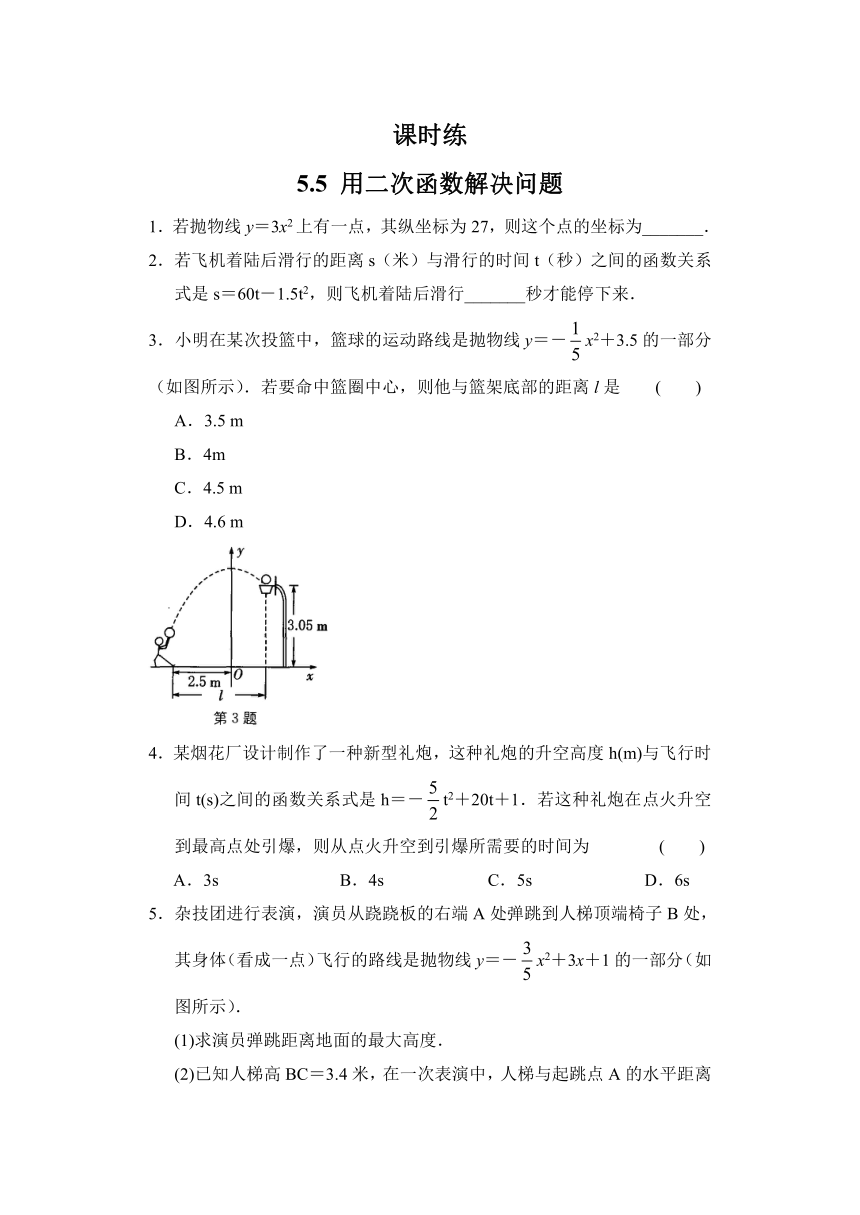 | |
| 格式 | zip | ||
| 文件大小 | 72.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-29 14:08:40 | ||
图片预览


文档简介
课时练
5.5 用二次函数解决问题
1.若抛物线y=3x2上有一点,其纵坐标为27,则这个点的坐标为_______.
2.若飞机着陆后滑行的距离s(米)与滑行的时间t(秒)之间的函数关系式是s=60t-1.5t2,则飞机着陆后滑行_______秒才能停下来.
3.小明在某次投篮中,篮球的运动路线是抛物线y=-x2+3.5的一部分(如图所示).若要命中篮圈中心,则他与篮架底部的距离l是 ( )
A.3.5 m
B.4m
C.4.5 m
D.4.6 m
4.某烟花厂设计制作了一种新型礼炮,这种礼炮的升空高度h(m)与飞行时间t(s)之间的函数关系式是h=-t2+20t+1.若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆所需要的时间为 ( )
A.3s B.4s C.5s D.6s
5.杂技团进行表演,演员从跷跷板的右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)飞行的路线是抛物线y=-x2+3x+1的一部分(如图所示).
(1)求演员弹跳距离地面的最大高度.
(2)已知人梯高BC=3.4米,在一次表演中,人梯与起跳点A的水平距离是4米,问这次表演能否成功?请说明理由.
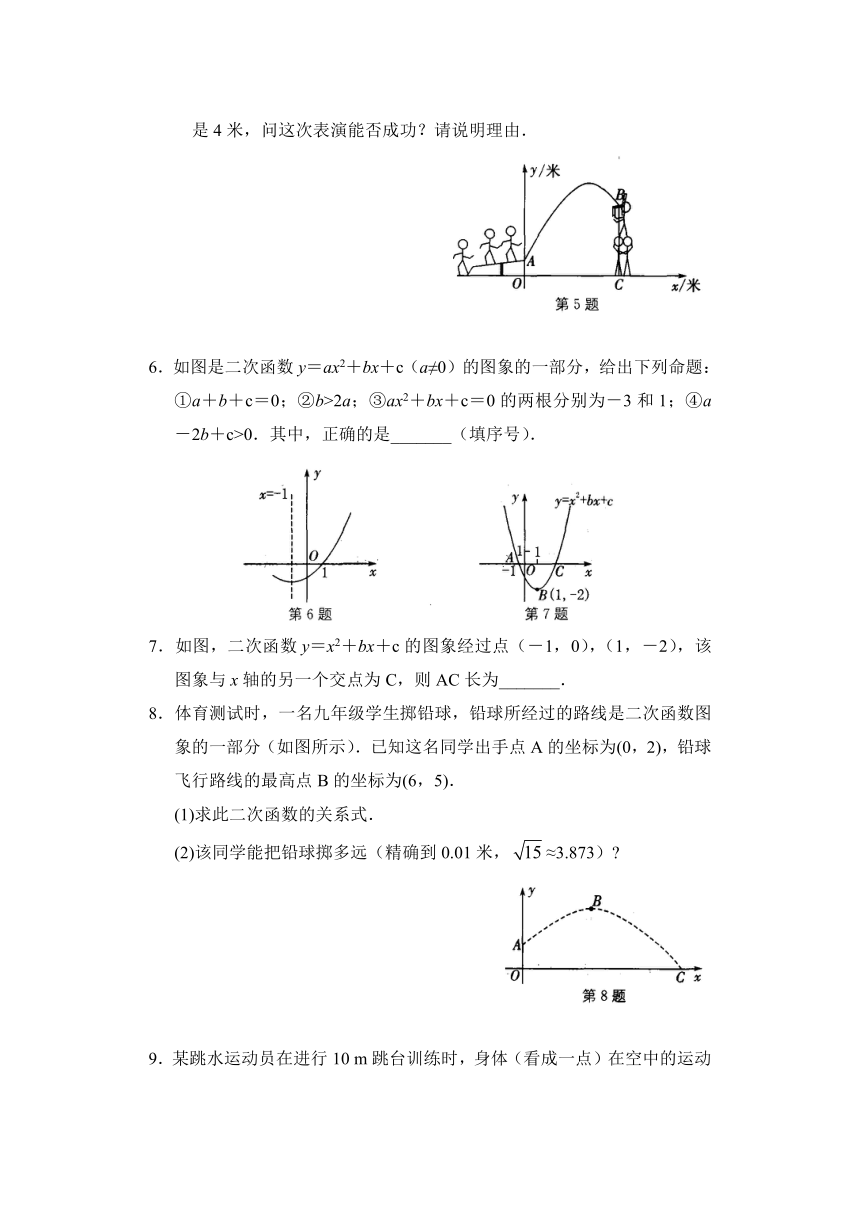
6.如图是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为-3和1;④a-2b+c>0.其中,正确的是_______(填序号).
7.如图,二次函数y=x2+bx+c的图象经过点(-1,0),(1,-2),该图象与x轴的另一个交点为C,则AC长为_______.
8.体育测试时,一名九年级学生掷铅球,铅球所经过的路线是二次函数图象的一部分(如图所示).已知这名同学出手点A的坐标为(0,2),铅球飞行路线的最高点B的坐标为(6,5).
(1)求此二次函数的关系式.
(2)该同学能把铅球掷多远(精确到0.01米,≈3.873)
9.某跳水运动员在进行10 m跳台训练时,身体(看成一点)在空中的运动路线可以看做是直角坐标系中经过原点O的一条抛物线(如图所示,图中标出的数据为已知条件).在跳某个规定动作时,正常情况下,该运动员在空中最高处距水面10m,入水处与池边的水平距离为4 m.同时,运动员在距水面的高度为5m以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.
(1)求此抛物线对应的函数关系式.
(2)在某次试跳中,测得运动员在空中的运动路线是(1)中的抛物线,且运动员在空中调整好入水姿势时,距池边的水平距离为3 m,则此次试跳会不会失误?请通过计算说明理由.
10.如图,小明在一次高尔夫球争霸赛中,从山坡下0点打出一球向球洞A点飞去,球的飞行路线为抛物线,如果不考虑空气阻力,那么当球达到最大高度12米时,球移动的水平距离为9米,已知山坡OA与水平方向OC的夹角为30°,O、A两点间相距8米.
(1)求出点A的坐标及直线OA对应的函数关系式.
(2)求出球的飞行路线所在的抛物线对应的函数关系式.
(3)试判断小明这一杆能否把高尔夫球从O点直接打入球洞A点.
11.已知直线y=kx+3(k<0)分别交x轴、y轴于A、B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,过点P作x轴的垂线交直线AB于点C,设运动时间为t秒.
(1)当k=-1时,线段OA上另有一动点Q由点A向点O运动,它与点P以相同速度同时出发,当点P到达点A时两点同时停止运动(如图①所示).
①直接写出当t=1秒时,C、Q两点的坐标,
②若以Q、C、A为顶点的三角形与△AOB相似,求t的值.
(2)当k=-时,设以C为顶点的抛物线y=(x+m)2+n与直线AB的另一交点为D(如图②所示).
①求CD的长.
②设△COD的OC边上的高为h,当t为何值时,h的值最大?
(
(第
11
题图
2
)
(第
11
题图
1
)
)
参考答案
1.(3,27)或(-3,27) 2.40 3.B 4.B 5.(1) 演员弹跳距离地面的最大高度是米 (2)能
6.①③ 7.3 8.(l)y=- (x-6)2+5 (2)13.75米
9.(1)(0≤x≤2) (2)会失误 10.(1)点A的坐标为(12,4).y=x
(2) (3)不能 11.(1) ①C(1,2),Q(2,0) ②1.5秒或2秒 (2)① ②当t为 秒时,h的值最大
5.5 用二次函数解决问题
1.若抛物线y=3x2上有一点,其纵坐标为27,则这个点的坐标为_______.
2.若飞机着陆后滑行的距离s(米)与滑行的时间t(秒)之间的函数关系式是s=60t-1.5t2,则飞机着陆后滑行_______秒才能停下来.
3.小明在某次投篮中,篮球的运动路线是抛物线y=-x2+3.5的一部分(如图所示).若要命中篮圈中心,则他与篮架底部的距离l是 ( )
A.3.5 m
B.4m
C.4.5 m
D.4.6 m
4.某烟花厂设计制作了一种新型礼炮,这种礼炮的升空高度h(m)与飞行时间t(s)之间的函数关系式是h=-t2+20t+1.若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆所需要的时间为 ( )
A.3s B.4s C.5s D.6s
5.杂技团进行表演,演员从跷跷板的右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)飞行的路线是抛物线y=-x2+3x+1的一部分(如图所示).
(1)求演员弹跳距离地面的最大高度.
(2)已知人梯高BC=3.4米,在一次表演中,人梯与起跳点A的水平距离是4米,问这次表演能否成功?请说明理由.
6.如图是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为-3和1;④a-2b+c>0.其中,正确的是_______(填序号).
7.如图,二次函数y=x2+bx+c的图象经过点(-1,0),(1,-2),该图象与x轴的另一个交点为C,则AC长为_______.
8.体育测试时,一名九年级学生掷铅球,铅球所经过的路线是二次函数图象的一部分(如图所示).已知这名同学出手点A的坐标为(0,2),铅球飞行路线的最高点B的坐标为(6,5).
(1)求此二次函数的关系式.
(2)该同学能把铅球掷多远(精确到0.01米,≈3.873)
9.某跳水运动员在进行10 m跳台训练时,身体(看成一点)在空中的运动路线可以看做是直角坐标系中经过原点O的一条抛物线(如图所示,图中标出的数据为已知条件).在跳某个规定动作时,正常情况下,该运动员在空中最高处距水面10m,入水处与池边的水平距离为4 m.同时,运动员在距水面的高度为5m以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.
(1)求此抛物线对应的函数关系式.
(2)在某次试跳中,测得运动员在空中的运动路线是(1)中的抛物线,且运动员在空中调整好入水姿势时,距池边的水平距离为3 m,则此次试跳会不会失误?请通过计算说明理由.
10.如图,小明在一次高尔夫球争霸赛中,从山坡下0点打出一球向球洞A点飞去,球的飞行路线为抛物线,如果不考虑空气阻力,那么当球达到最大高度12米时,球移动的水平距离为9米,已知山坡OA与水平方向OC的夹角为30°,O、A两点间相距8米.
(1)求出点A的坐标及直线OA对应的函数关系式.
(2)求出球的飞行路线所在的抛物线对应的函数关系式.
(3)试判断小明这一杆能否把高尔夫球从O点直接打入球洞A点.
11.已知直线y=kx+3(k<0)分别交x轴、y轴于A、B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,过点P作x轴的垂线交直线AB于点C,设运动时间为t秒.
(1)当k=-1时,线段OA上另有一动点Q由点A向点O运动,它与点P以相同速度同时出发,当点P到达点A时两点同时停止运动(如图①所示).
①直接写出当t=1秒时,C、Q两点的坐标,
②若以Q、C、A为顶点的三角形与△AOB相似,求t的值.
(2)当k=-时,设以C为顶点的抛物线y=(x+m)2+n与直线AB的另一交点为D(如图②所示).
①求CD的长.
②设△COD的OC边上的高为h,当t为何值时,h的值最大?
(
(第
11
题图
2
)
(第
11
题图
1
)
)
参考答案
1.(3,27)或(-3,27) 2.40 3.B 4.B 5.(1) 演员弹跳距离地面的最大高度是米 (2)能
6.①③ 7.3 8.(l)y=- (x-6)2+5 (2)13.75米
9.(1)(0≤x≤2) (2)会失误 10.(1)点A的坐标为(12,4).y=x
(2) (3)不能 11.(1) ①C(1,2),Q(2,0) ②1.5秒或2秒 (2)① ②当t为 秒时,h的值最大
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
