2022-2023学年山东省东营市垦利区八年级(上)期中数学试卷(五四学制)(word,含解析)
文档属性
| 名称 | 2022-2023学年山东省东营市垦利区八年级(上)期中数学试卷(五四学制)(word,含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 240.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-29 08:44:10 | ||
图片预览




文档简介
2022-2023学年山东省东营市垦利区八年级(上)期中数学试卷(五四学制)
一、选择题(本题共10小题,共30分,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来。每小题选对得3分,不选或选出的答案超过一个均记零分。)
1.下列各式:①x2﹣16=(x+4)(x﹣4),②(a+b)2=a2+2ab+b2,③a2b﹣ab2=ab(a﹣b).从左到右的变形中,属于因式分解的是( )
A.② B.①② C.①③ D.②③
2.下列分式是最简分式的是( )
A. B. C. D.
3.甲、乙、丙、丁四人进行射击测试,每人射击10次,四人的平均成绩均是9.4环,方差分别是0.43,1.13,0.90,1.68,则在本次射击测试中,成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
4.下列各多项式中,能用公式法分解因式的是( )
A.a2﹣b2+2ab B.a2+b2+ab C.4a2+12a+9 D.25n2+15n+9
5.某班要推选学生参加学校的“诗词达人”比赛,有7名学生报名参加班级选拔赛,他们的选拔赛成绩各不相同,现取其中前3名参加学校比赛.小红要判断自己能否参加学校比赛,在知道自己成绩的情况下,还需要知道这7名学生成绩的( )
A.众数 B.中位数 C.平均数 D.方差
6.小强是一位密码编译爱好者,在他的密码手册中,有这样一条信息:a﹣b,x﹣y,x+y,a+b,x2﹣y2,a2﹣b2分别对应下列六个字:利、爱、我、垦、游、美,现将(x2﹣y2)a2﹣(x2﹣y2)b2因式分解,结果呈现的密码信息可能是( )
A.爱我垦利 B.游我垦利 C.游美垦利 D.游美
7.一组数据:﹣1、2、3、1、0,则这组数据平均数和方差分别是( )
A.1,1.8 B.1.8,1 C.2,1 D.1,2
8.已知x2﹣kxy+64y2可以配方成完全平方,则k的值是( )
A.16 B.±16 C.±8 D.8
9.已知样本x1,x2,x3,…,xn的方差是1,那么样本2x1+3,2x2+3,2x3+3,…,2xn+3的方差是( )
A.1 B.2 C.3 D.4
10.如果分式方程无解,则a的值为( )
A.﹣4 B. C.2 D.﹣2
二、填空题:(本大题共8小题,其中11-14题每小题3分,15-18题每小题3分,共28分.只要求填写最后结果.)
11.(3分)若分式的值为0,则a的值为 .
12.(3分)小明本学期平时测验,期中考试和期末考试的数学成绩分别是102分、114分、110分.如果这3项成绩分别按30%、30%、40%的比例计算,那么小明本学期的数学平均分是 .
13.(3分)已知x+y=6,xy=7,则x2y+xy2的值是 .
14.(3分)已知一组数据的方差s2=[(x1﹣6)2+(x2﹣6)2+(x3﹣6)2+(x4﹣6)2],那么这组数据的总和为 .
15.(3分)多项式x2+mx+6因式分解得(x﹣2)(x+n),则m= .
16.为响应国家“乡村旅游振兴”战略号召,几名同学准备参加“大美青海”旅游活动,包租一辆面包车从西宁前往青海湖.面包车的租价为240元,出发时又增加了4名同学,每人比原来少分担了10元车费.设原有人数为x人,则可列方程 .
17.在实数范围内分解因式:2x3﹣6x= .
18.观察下列等式:,,,……计算的结果为 .
三、解答题:(本大题共7小题,共62分。解答要写出必要的文字说明,证明过程或演算步骤)
19.(1)20222﹣2021×2023 (用简便方法计算);
(2)解方程:=﹣2.
20.(8分)化简求值:(﹣x+1)÷,其中x从0、2、﹣1中任意取一个数求值.
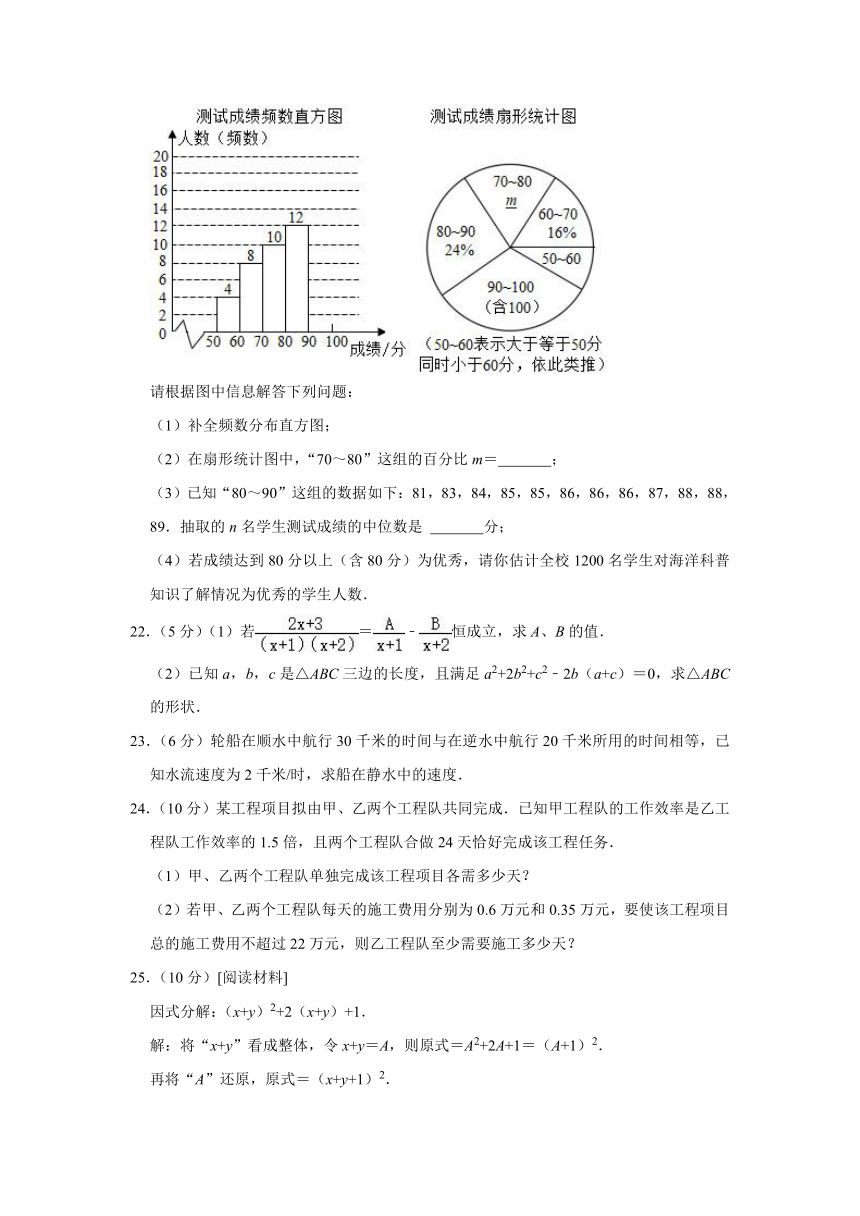
21.(10分)某校为调查学生对海洋科普知识的了解情况,从全校学生中随机抽取n名学生进行测试,测试成绩进行整理后分成五组,并绘制成如图的频数分布直方图和扇形统计图.
请根据图中信息解答下列问题:
(1)补全频数分布直方图;
(2)在扇形统计图中,“70~80”这组的百分比m= ;
(3)已知“80~90”这组的数据如下:81,83,84,85,85,86,86,86,87,88,88,89.抽取的n名学生测试成绩的中位数是 分;
(4)若成绩达到80分以上(含80分)为优秀,请你估计全校1200名学生对海洋科普知识了解情况为优秀的学生人数.
22.(5分)(1)若=﹣恒成立,求A、B的值.
(2)已知a,b,c是△ABC三边的长度,且满足a2+2b2+c2﹣2b(a+c)=0,求△ABC的形状.
23.(6分)轮船在顺水中航行30千米的时间与在逆水中航行20千米所用的时间相等,已知水流速度为2千米/时,求船在静水中的速度.
24.(10分)某工程项目拟由甲、乙两个工程队共同完成.已知甲工程队的工作效率是乙工程队工作效率的1.5倍,且两个工程队合做24天恰好完成该工程任务.
(1)甲、乙两个工程队单独完成该工程项目各需多少天?
(2)若甲、乙两个工程队每天的施工费用分别为0.6万元和0.35万元,要使该工程项目总的施工费用不超过22万元,则乙工程队至少需要施工多少天?
25.(10分)[阅读材料]
因式分解:(x+y)2+2(x+y)+1.
解:将“x+y”看成整体,令x+y=A,则原式=A2+2A+1=(A+1)2.
再将“A”还原,原式=(x+y+1)2.
上述解题用到的是“整体思想”,整体思想是数学解题中常用的一种思想方法.
[问题解决]
(1)因式分解:1+4(x﹣y)+4(x﹣y)2;
(2)因式分解:(x2﹣6x)(x2﹣6x+18)+81;
(3)证明:若n为正整数,则代数式(n+1)(n+2)(n2+3n)+1的值一定是某个整数的平方.
2022-2023学年山东省东营市垦利区八年级(上)期中数学试卷(五四学制)
参考答案与试题解析
一、选择题(本题共10小题,共30分,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来。每小题选对得3分,不选或选出的答案超过一个均记零分。)
1.下列各式:①x2﹣16=(x+4)(x﹣4),②(a+b)2=a2+2ab+b2,③a2b﹣ab2=ab(a﹣b).从左到右的变形中,属于因式分解的是( )
A.② B.①② C.①③ D.②③
【分析】根据因式分解是把一个多项式转化成几个整式的积的形式,可得答案.
【解答】解:①是因式分解;
②是整式的乘法;
③是因式分解;
故选:C.
2.下列分式是最简分式的是( )
A. B. C. D.
【分析】结合最简分式的定义:一个分式的分子与分母没有公因式时,叫最简分式.求解即可.
【解答】解:A、=2x,不是最简分式,本选项错误;
B、=,不是最简分式,本选项错误;
C、是最简分式,本选项正确;
D、=﹣1,不是最简分式,本选项错误.
故选:C.
3.甲、乙、丙、丁四人进行射击测试,每人射击10次,四人的平均成绩均是9.4环,方差分别是0.43,1.13,0.90,1.68,则在本次射击测试中,成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
【分析】根据方差的定义,方差越小数据越稳定.
【解答】解:∵=0.43,=1.13,=0.90,=1.68,
∴>>>,
∴成绩最稳定的是甲.
故选:A.
4.下列各多项式中,能用公式法分解因式的是( )
A.a2﹣b2+2ab B.a2+b2+ab C.4a2+12a+9 D.25n2+15n+9
【分析】利用完全平方公式及平方差公式判断即可.
【解答】解:A、原式不能利用公式分解;
B、原式不能利用公式分解;
C、原式=(2a+3)2,符合题意;
D、原式不能利用公式分解,
故选:C.
5.某班要推选学生参加学校的“诗词达人”比赛,有7名学生报名参加班级选拔赛,他们的选拔赛成绩各不相同,现取其中前3名参加学校比赛.小红要判断自己能否参加学校比赛,在知道自己成绩的情况下,还需要知道这7名学生成绩的( )
A.众数 B.中位数 C.平均数 D.方差
【分析】由于总共有7个人,且他们的成绩互不相同,第4的成绩是中位数,要判断自己能否参加学校比赛,只需知道中位数即可.
【解答】解:由于总共有7个人,且他们的成绩互不相同,第4的成绩是中位数,要判断自己能否参加学校比赛,
故应知道中位数的多少.
故选:B.
6.小强是一位密码编译爱好者,在他的密码手册中,有这样一条信息:a﹣b,x﹣y,x+y,a+b,x2﹣y2,a2﹣b2分别对应下列六个字:利、爱、我、垦、游、美,现将(x2﹣y2)a2﹣(x2﹣y2)b2因式分解,结果呈现的密码信息可能是( )
A.爱我垦利 B.游我垦利 C.游美垦利 D.游美
【分析】先把代数式分解因式,再找对应因式所对的汉字.
【解答】解:(x2﹣y2)a2﹣(x2﹣y2)b2
=(x2﹣y2)(a2﹣b2)
=(x+y)(x﹣y)(a+b)(a﹣b),
∴结果呈现的密码信息可能是:爱我垦利,
故选:A.
7.一组数据:﹣1、2、3、1、0,则这组数据平均数和方差分别是( )
A.1,1.8 B.1.8,1 C.2,1 D.1,2
【分析】先根据平均数的定义计算出这组数据的平均数,然后根据方差公式计算这组数据的方差.
【解答】解:这组数据平均数=(﹣1+2+3+1+0)=1,
数据的方差=[(﹣1﹣1)2+(2﹣1)2+(3﹣1)2+(1﹣1)2+(0﹣1)2]=2.
故选:D.
8.已知x2﹣kxy+64y2可以配方成完全平方,则k的值是( )
A.16 B.±16 C.±8 D.8
【分析】利用完全平方公式的结构特征判断即可得到k的值.
【解答】解:根据题意,x2﹣kxy+64y2可以配方成完全平方,
∵64y2=(±8y)2,
∴原式可化成(x±8y)2,
即x2±16xy+64y2,
∴﹣kxy=±16xy,
∴k=±16.
故选:B.
9.已知样本x1,x2,x3,…,xn的方差是1,那么样本2x1+3,2x2+3,2x3+3,…,2xn+3的方差是( )
A.1 B.2 C.3 D.4
【分析】根据方差的意义分析,数据都加3,方差不变,原数据都乘2,则方差是原来的4倍.
【解答】解:设样本x1,x2,x3,…,xn的平均数为m,
则其方差为S12=[(x1﹣m)2+(x2﹣m)2+…+(xn﹣m)2]=1,
则样本2x1+3,2x2+3,2x3+3,…,2xn+3的平均数为2m+3,其方差为S22=4S12=4.
故选:D.
10.如果分式方程无解,则a的值为( )
A.﹣4 B. C.2 D.﹣2
【分析】关于x的分式方程=2+无解,即分式方程去掉分母化为整式方程,整式方程的解就是方程的增根,即x=4,据此即可求解.
【解答】解:去分母得:x=2(x﹣4)﹣a
解得:x=a+8
根据题意得:a+8=4
解得:a=﹣4.
故选:A.
二、填空题:(本大题共8小题,其中11-14题每小题3分,15-18题每小题3分,共28分.只要求填写最后结果.)
11.(3分)若分式的值为0,则a的值为 ﹣3 .
【分析】根据分式的值为零的条件:分子等于0且分母不等于0即可得出答案.
【解答】解:根据题意得a2﹣9=0,a﹣3≠0,
∴a=﹣3,
故答案为:﹣3.
12.(3分)小明本学期平时测验,期中考试和期末考试的数学成绩分别是102分、114分、110分.如果这3项成绩分别按30%、30%、40%的比例计算,那么小明本学期的数学平均分是 108.8. .
【分析】按照所给的比例进行计算即可,小明本学期的数学学习成绩=平时测试×30%+期中考试×30%+期末考试×40%.
【解答】解:小明本学期的数学学习成绩=102×30%+114×30%+110×40%=108.8(分).
故答案为:108.8.
13.(3分)已知x+y=6,xy=7,则x2y+xy2的值是 42 .
【分析】将所求式子因式分解,然后将x+y=6,xy=7代入,即可解答本题.
【解答】解:∵x+y=6,xy=7,
∴x2y+xy2
=xy(x+y)
=7×6
=42,
故答案为:42.
14.(3分)已知一组数据的方差s2=[(x1﹣6)2+(x2﹣6)2+(x3﹣6)2+(x4﹣6)2],那么这组数据的总和为 24 .
【分析】根据方差公式S2=[(x1﹣)2+(x2﹣)2+…+(xn﹣)2]中各个字母表示的意义,得出这组数据的平均数是6,数据个数是4,从而得出这组数据的总和.
【解答】解:∵s2=[(x1﹣6)2+(x2﹣6)2+(x3﹣6)2+(x4﹣6)2],
∴这组数据的平均数是6,数据个数是4,
∴这组数据的总和为4×6=24;
故答案为:24.
15.(3分)多项式x2+mx+6因式分解得(x﹣2)(x+n),则m= ﹣5 .
【分析】根据因式分解是把一个多项式转化成几个整式积,可得答案.
【解答】解:x2+mx+6因式分解得(x﹣2)(x+n),得
x2+mx+6=(x﹣2)(x+n),(x﹣2)(x+n)=x2+(n﹣2)x﹣2n,
x2+mx+6=x2+(n﹣2)x﹣2n,
﹣2n=6,m=n﹣2.
解得n=﹣3,m=﹣5,
故答案为:﹣5.
16.为响应国家“乡村旅游振兴”战略号召,几名同学准备参加“大美青海”旅游活动,包租一辆面包车从西宁前往青海湖.面包车的租价为240元,出发时又增加了4名同学,每人比原来少分担了10元车费.设原有人数为x人,则可列方程 ﹣=10 .
【分析】利用人均分担的费用=租车费用÷人数,结合又增加了4名同学后比原来少分担了每人10元车费,即可得出关于x的分式方程,此题得解.
【解答】解:依题意得:﹣=10.
故答案为:﹣=10.
17.在实数范围内分解因式:2x3﹣6x= 2x(x+)(x﹣) .
【分析】先提公因式,然后利用平方差公式分解.
【解答】解:原式=2x(x2﹣3)
=2x(x+)(x﹣).
故答案为
18.观察下列等式:,,,……计算的结果为 .
【分析】由所给式子可将所求式子化为:(﹣+﹣+﹣+﹣)即可求解.
【解答】解:=(﹣+﹣+﹣+﹣)=(﹣)=,
故答案为.
三、解答题:(本大题共7小题,共62分。解答要写出必要的文字说明,证明过程或演算步骤)
19.(1)20222﹣2021×2023 (用简便方法计算);
(2)解方程:=﹣2.
【分析】(1)根据平方差公式简化运算即可;
(2)根据解分式方程的步骤求解即可.
【解答】解:(1)20222﹣2021×2023
=20222﹣(2022﹣1)×(2022+1)
=20222﹣20222+1
=1;
(2)去分母,得2﹣x=﹣1﹣2(x﹣3),
解得x=3,
经检验,x=3是原方程的增根,
∴原方程无解.
20.(8分)化简求值:(﹣x+1)÷,其中x从0、2、﹣1中任意取一个数求值.
【分析】先算括号内的加减,把除法变成乘法,算乘法,最后代入求出答案即可.
【解答】解:(﹣x+1)÷
=
=
=﹣,
∵从分式知:x+1≠0,x﹣2≠0,
∴x≠﹣1且x≠2,
取x=0,
当x=0时,原式=﹣=1.
21.(10分)某校为调查学生对海洋科普知识的了解情况,从全校学生中随机抽取n名学生进行测试,测试成绩进行整理后分成五组,并绘制成如图的频数分布直方图和扇形统计图.
请根据图中信息解答下列问题:
(1)补全频数分布直方图;
(2)在扇形统计图中,“70~80”这组的百分比m= 20% ;
(3)已知“80~90”这组的数据如下:81,83,84,85,85,86,86,86,87,88,88,89.抽取的n名学生测试成绩的中位数是 84.5 分;
(4)若成绩达到80分以上(含80分)为优秀,请你估计全校1200名学生对海洋科普知识了解情况为优秀的学生人数.
【分析】(1)求出调查人数,和“90﹣100”的人数即可补全频数分布直方图;
(2)用“70﹣80”的频数10除以调查人数50 即可得出m的值;
(3)利用中位数的意义,求出中间位置的两个数的平均数,即可得出中位数;
(4)样本估计总体,样本中优秀所占的百分比为,因此估计总体1200人的是优秀的人数.
【解答】解:(1)8÷16%=50(人),50﹣4﹣8﹣10﹣12=16(人),补全频数分布直方图如图所示:
(2)m=10÷50=20%,
故答案为:20%;
(3)将50个数据从小到大排列后,处在第25、26位的两个数的平均数为=84.5,
因此中位数是84.5,
故答案为:84.5;
(4)1200×=672(人),
答:估计全校1200名学生对海洋科普知识了解情况为优秀的学生大约有672人.
22.(5分)(1)若=﹣恒成立,求A、B的值.
(2)已知a,b,c是△ABC三边的长度,且满足a2+2b2+c2﹣2b(a+c)=0,求△ABC的形状.
【分析】(1)先把等式右边通分,再根据多项式相等,对应项的系数相等,列方程求解;
(2)先把等号左边配方,再根据平方的非负性求解.
【解答】解:(1)∵=﹣=,
∴2x+3=Ax+2A﹣Bx﹣B=(A﹣B)x+(2A﹣B),
∴A﹣B=2且2A﹣B=3,
解得:A=1,B=﹣1;
(2)∵a2+2b2+c2﹣2b(a+c)
=a2+2b2+c2﹣2ba﹣2bc
=(a﹣b)2+(b﹣c)2=0,
∴a=b=c,
∴△ABC的形状为等边三角形.
23.(6分)轮船在顺水中航行30千米的时间与在逆水中航行20千米所用的时间相等,已知水流速度为2千米/时,求船在静水中的速度.
【分析】设船在静水中的速度是x千米/小时,根据轮船在顺水中航行30千米的时间与在逆水中航行20千米所用的时间相等,已知水流速度为2千米/小时,可列方程求解.
【解答】解:设船在静水中的速度是x千米/小时,
根据题意得,=,
x=10,
经检验x=10是分式方程的解.
所以船在静水中的速度是10千米/小时.
24.(10分)某工程项目拟由甲、乙两个工程队共同完成.已知甲工程队的工作效率是乙工程队工作效率的1.5倍,且两个工程队合做24天恰好完成该工程任务.
(1)甲、乙两个工程队单独完成该工程项目各需多少天?
(2)若甲、乙两个工程队每天的施工费用分别为0.6万元和0.35万元,要使该工程项目总的施工费用不超过22万元,则乙工程队至少需要施工多少天?
【分析】(1)设甲工程队单独完成此项目需x天,乙工程队单独完成此项目需y天.由题意:甲工程队的工作效率是乙工程队工作效率的1.5倍,且两个工程队合做24天恰好完成该工程任务.列出分式方程组,解分式方程组即可;
(2)设甲工程队施工a天,乙工程队施工b天时,由甲、乙两队的工作量之和为1及总费用不超过22万元两个关系进行分析即可.
【解答】解:(1)设甲工程队单独完成此项目需x天,乙工程队单独完成此项目需y天.
依题意得:,
解得:,
经检验,是原方程组的解,且符合题意.
答:甲工程队单独完成此项目需40天,乙工程队单独完成此项目需60天.
(2)设甲工程队施工a天,乙工程队施工b天时,总的施工费用不超过22万元.
根据题意得:,
解得:b≥40.
答:要使该项目总的施工费用不超过22万元,乙工程队最少施工40天.
25.(10分)[阅读材料]
因式分解:(x+y)2+2(x+y)+1.
解:将“x+y”看成整体,令x+y=A,则原式=A2+2A+1=(A+1)2.
再将“A”还原,原式=(x+y+1)2.
上述解题用到的是“整体思想”,整体思想是数学解题中常用的一种思想方法.
[问题解决]
(1)因式分解:1+4(x﹣y)+4(x﹣y)2;
(2)因式分解:(x2﹣6x)(x2﹣6x+18)+81;
(3)证明:若n为正整数,则代数式(n+1)(n+2)(n2+3n)+1的值一定是某个整数的平方.
【分析】(1)用换元法设x﹣y=A,将原式化为1+4Α+4Α2,再利用完全平方公式得出(1+2A)2,再将A 还原即可;
(2)设 x2﹣6x=B,则原式=B(B+18)+81=B2+18B+81=(B+9)2后,再将B还原后,最后再利用完全平方公式即可;
(3)先计算(n+1)(n+2)=n2+3n+2,再利用完全平方公式即可.
【解答】解:(1)令x﹣y=A,
原式=1+4Α+4Α2
=(1+2A)2
=(1+2x﹣2y)2;
(2)令 a2﹣4a=B,
则原式=B(B+18)+81
=B2+18B+81
=(B+9)2
=(x2﹣6x+9)2
=(x﹣3)4;
(3)证明:原式=(n2+3n+2)(n2+3n)+1
=(n2+3n)2+2(n2+3n)+1
=(n2+3n+1)2,
∵n为正整数,
∴n2+3n+1为正整数.
∴(n+1)(n+2)(n2+3n)=(n2+3n+1)2,
即代数(n+1)(n+2)(n2+3n)+1的值一定是某个整数的平方.
一、选择题(本题共10小题,共30分,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来。每小题选对得3分,不选或选出的答案超过一个均记零分。)
1.下列各式:①x2﹣16=(x+4)(x﹣4),②(a+b)2=a2+2ab+b2,③a2b﹣ab2=ab(a﹣b).从左到右的变形中,属于因式分解的是( )
A.② B.①② C.①③ D.②③
2.下列分式是最简分式的是( )
A. B. C. D.
3.甲、乙、丙、丁四人进行射击测试,每人射击10次,四人的平均成绩均是9.4环,方差分别是0.43,1.13,0.90,1.68,则在本次射击测试中,成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
4.下列各多项式中,能用公式法分解因式的是( )
A.a2﹣b2+2ab B.a2+b2+ab C.4a2+12a+9 D.25n2+15n+9
5.某班要推选学生参加学校的“诗词达人”比赛,有7名学生报名参加班级选拔赛,他们的选拔赛成绩各不相同,现取其中前3名参加学校比赛.小红要判断自己能否参加学校比赛,在知道自己成绩的情况下,还需要知道这7名学生成绩的( )
A.众数 B.中位数 C.平均数 D.方差
6.小强是一位密码编译爱好者,在他的密码手册中,有这样一条信息:a﹣b,x﹣y,x+y,a+b,x2﹣y2,a2﹣b2分别对应下列六个字:利、爱、我、垦、游、美,现将(x2﹣y2)a2﹣(x2﹣y2)b2因式分解,结果呈现的密码信息可能是( )
A.爱我垦利 B.游我垦利 C.游美垦利 D.游美
7.一组数据:﹣1、2、3、1、0,则这组数据平均数和方差分别是( )
A.1,1.8 B.1.8,1 C.2,1 D.1,2
8.已知x2﹣kxy+64y2可以配方成完全平方,则k的值是( )
A.16 B.±16 C.±8 D.8
9.已知样本x1,x2,x3,…,xn的方差是1,那么样本2x1+3,2x2+3,2x3+3,…,2xn+3的方差是( )
A.1 B.2 C.3 D.4
10.如果分式方程无解,则a的值为( )
A.﹣4 B. C.2 D.﹣2
二、填空题:(本大题共8小题,其中11-14题每小题3分,15-18题每小题3分,共28分.只要求填写最后结果.)
11.(3分)若分式的值为0,则a的值为 .
12.(3分)小明本学期平时测验,期中考试和期末考试的数学成绩分别是102分、114分、110分.如果这3项成绩分别按30%、30%、40%的比例计算,那么小明本学期的数学平均分是 .
13.(3分)已知x+y=6,xy=7,则x2y+xy2的值是 .
14.(3分)已知一组数据的方差s2=[(x1﹣6)2+(x2﹣6)2+(x3﹣6)2+(x4﹣6)2],那么这组数据的总和为 .
15.(3分)多项式x2+mx+6因式分解得(x﹣2)(x+n),则m= .
16.为响应国家“乡村旅游振兴”战略号召,几名同学准备参加“大美青海”旅游活动,包租一辆面包车从西宁前往青海湖.面包车的租价为240元,出发时又增加了4名同学,每人比原来少分担了10元车费.设原有人数为x人,则可列方程 .
17.在实数范围内分解因式:2x3﹣6x= .
18.观察下列等式:,,,……计算的结果为 .
三、解答题:(本大题共7小题,共62分。解答要写出必要的文字说明,证明过程或演算步骤)
19.(1)20222﹣2021×2023 (用简便方法计算);
(2)解方程:=﹣2.
20.(8分)化简求值:(﹣x+1)÷,其中x从0、2、﹣1中任意取一个数求值.
21.(10分)某校为调查学生对海洋科普知识的了解情况,从全校学生中随机抽取n名学生进行测试,测试成绩进行整理后分成五组,并绘制成如图的频数分布直方图和扇形统计图.
请根据图中信息解答下列问题:
(1)补全频数分布直方图;
(2)在扇形统计图中,“70~80”这组的百分比m= ;
(3)已知“80~90”这组的数据如下:81,83,84,85,85,86,86,86,87,88,88,89.抽取的n名学生测试成绩的中位数是 分;
(4)若成绩达到80分以上(含80分)为优秀,请你估计全校1200名学生对海洋科普知识了解情况为优秀的学生人数.
22.(5分)(1)若=﹣恒成立,求A、B的值.
(2)已知a,b,c是△ABC三边的长度,且满足a2+2b2+c2﹣2b(a+c)=0,求△ABC的形状.
23.(6分)轮船在顺水中航行30千米的时间与在逆水中航行20千米所用的时间相等,已知水流速度为2千米/时,求船在静水中的速度.
24.(10分)某工程项目拟由甲、乙两个工程队共同完成.已知甲工程队的工作效率是乙工程队工作效率的1.5倍,且两个工程队合做24天恰好完成该工程任务.
(1)甲、乙两个工程队单独完成该工程项目各需多少天?
(2)若甲、乙两个工程队每天的施工费用分别为0.6万元和0.35万元,要使该工程项目总的施工费用不超过22万元,则乙工程队至少需要施工多少天?
25.(10分)[阅读材料]
因式分解:(x+y)2+2(x+y)+1.
解:将“x+y”看成整体,令x+y=A,则原式=A2+2A+1=(A+1)2.
再将“A”还原,原式=(x+y+1)2.
上述解题用到的是“整体思想”,整体思想是数学解题中常用的一种思想方法.
[问题解决]
(1)因式分解:1+4(x﹣y)+4(x﹣y)2;
(2)因式分解:(x2﹣6x)(x2﹣6x+18)+81;
(3)证明:若n为正整数,则代数式(n+1)(n+2)(n2+3n)+1的值一定是某个整数的平方.
2022-2023学年山东省东营市垦利区八年级(上)期中数学试卷(五四学制)
参考答案与试题解析
一、选择题(本题共10小题,共30分,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来。每小题选对得3分,不选或选出的答案超过一个均记零分。)
1.下列各式:①x2﹣16=(x+4)(x﹣4),②(a+b)2=a2+2ab+b2,③a2b﹣ab2=ab(a﹣b).从左到右的变形中,属于因式分解的是( )
A.② B.①② C.①③ D.②③
【分析】根据因式分解是把一个多项式转化成几个整式的积的形式,可得答案.
【解答】解:①是因式分解;
②是整式的乘法;
③是因式分解;
故选:C.
2.下列分式是最简分式的是( )
A. B. C. D.
【分析】结合最简分式的定义:一个分式的分子与分母没有公因式时,叫最简分式.求解即可.
【解答】解:A、=2x,不是最简分式,本选项错误;
B、=,不是最简分式,本选项错误;
C、是最简分式,本选项正确;
D、=﹣1,不是最简分式,本选项错误.
故选:C.
3.甲、乙、丙、丁四人进行射击测试,每人射击10次,四人的平均成绩均是9.4环,方差分别是0.43,1.13,0.90,1.68,则在本次射击测试中,成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
【分析】根据方差的定义,方差越小数据越稳定.
【解答】解:∵=0.43,=1.13,=0.90,=1.68,
∴>>>,
∴成绩最稳定的是甲.
故选:A.
4.下列各多项式中,能用公式法分解因式的是( )
A.a2﹣b2+2ab B.a2+b2+ab C.4a2+12a+9 D.25n2+15n+9
【分析】利用完全平方公式及平方差公式判断即可.
【解答】解:A、原式不能利用公式分解;
B、原式不能利用公式分解;
C、原式=(2a+3)2,符合题意;
D、原式不能利用公式分解,
故选:C.
5.某班要推选学生参加学校的“诗词达人”比赛,有7名学生报名参加班级选拔赛,他们的选拔赛成绩各不相同,现取其中前3名参加学校比赛.小红要判断自己能否参加学校比赛,在知道自己成绩的情况下,还需要知道这7名学生成绩的( )
A.众数 B.中位数 C.平均数 D.方差
【分析】由于总共有7个人,且他们的成绩互不相同,第4的成绩是中位数,要判断自己能否参加学校比赛,只需知道中位数即可.
【解答】解:由于总共有7个人,且他们的成绩互不相同,第4的成绩是中位数,要判断自己能否参加学校比赛,
故应知道中位数的多少.
故选:B.
6.小强是一位密码编译爱好者,在他的密码手册中,有这样一条信息:a﹣b,x﹣y,x+y,a+b,x2﹣y2,a2﹣b2分别对应下列六个字:利、爱、我、垦、游、美,现将(x2﹣y2)a2﹣(x2﹣y2)b2因式分解,结果呈现的密码信息可能是( )
A.爱我垦利 B.游我垦利 C.游美垦利 D.游美
【分析】先把代数式分解因式,再找对应因式所对的汉字.
【解答】解:(x2﹣y2)a2﹣(x2﹣y2)b2
=(x2﹣y2)(a2﹣b2)
=(x+y)(x﹣y)(a+b)(a﹣b),
∴结果呈现的密码信息可能是:爱我垦利,
故选:A.
7.一组数据:﹣1、2、3、1、0,则这组数据平均数和方差分别是( )
A.1,1.8 B.1.8,1 C.2,1 D.1,2
【分析】先根据平均数的定义计算出这组数据的平均数,然后根据方差公式计算这组数据的方差.
【解答】解:这组数据平均数=(﹣1+2+3+1+0)=1,
数据的方差=[(﹣1﹣1)2+(2﹣1)2+(3﹣1)2+(1﹣1)2+(0﹣1)2]=2.
故选:D.
8.已知x2﹣kxy+64y2可以配方成完全平方,则k的值是( )
A.16 B.±16 C.±8 D.8
【分析】利用完全平方公式的结构特征判断即可得到k的值.
【解答】解:根据题意,x2﹣kxy+64y2可以配方成完全平方,
∵64y2=(±8y)2,
∴原式可化成(x±8y)2,
即x2±16xy+64y2,
∴﹣kxy=±16xy,
∴k=±16.
故选:B.
9.已知样本x1,x2,x3,…,xn的方差是1,那么样本2x1+3,2x2+3,2x3+3,…,2xn+3的方差是( )
A.1 B.2 C.3 D.4
【分析】根据方差的意义分析,数据都加3,方差不变,原数据都乘2,则方差是原来的4倍.
【解答】解:设样本x1,x2,x3,…,xn的平均数为m,
则其方差为S12=[(x1﹣m)2+(x2﹣m)2+…+(xn﹣m)2]=1,
则样本2x1+3,2x2+3,2x3+3,…,2xn+3的平均数为2m+3,其方差为S22=4S12=4.
故选:D.
10.如果分式方程无解,则a的值为( )
A.﹣4 B. C.2 D.﹣2
【分析】关于x的分式方程=2+无解,即分式方程去掉分母化为整式方程,整式方程的解就是方程的增根,即x=4,据此即可求解.
【解答】解:去分母得:x=2(x﹣4)﹣a
解得:x=a+8
根据题意得:a+8=4
解得:a=﹣4.
故选:A.
二、填空题:(本大题共8小题,其中11-14题每小题3分,15-18题每小题3分,共28分.只要求填写最后结果.)
11.(3分)若分式的值为0,则a的值为 ﹣3 .
【分析】根据分式的值为零的条件:分子等于0且分母不等于0即可得出答案.
【解答】解:根据题意得a2﹣9=0,a﹣3≠0,
∴a=﹣3,
故答案为:﹣3.
12.(3分)小明本学期平时测验,期中考试和期末考试的数学成绩分别是102分、114分、110分.如果这3项成绩分别按30%、30%、40%的比例计算,那么小明本学期的数学平均分是 108.8. .
【分析】按照所给的比例进行计算即可,小明本学期的数学学习成绩=平时测试×30%+期中考试×30%+期末考试×40%.
【解答】解:小明本学期的数学学习成绩=102×30%+114×30%+110×40%=108.8(分).
故答案为:108.8.
13.(3分)已知x+y=6,xy=7,则x2y+xy2的值是 42 .
【分析】将所求式子因式分解,然后将x+y=6,xy=7代入,即可解答本题.
【解答】解:∵x+y=6,xy=7,
∴x2y+xy2
=xy(x+y)
=7×6
=42,
故答案为:42.
14.(3分)已知一组数据的方差s2=[(x1﹣6)2+(x2﹣6)2+(x3﹣6)2+(x4﹣6)2],那么这组数据的总和为 24 .
【分析】根据方差公式S2=[(x1﹣)2+(x2﹣)2+…+(xn﹣)2]中各个字母表示的意义,得出这组数据的平均数是6,数据个数是4,从而得出这组数据的总和.
【解答】解:∵s2=[(x1﹣6)2+(x2﹣6)2+(x3﹣6)2+(x4﹣6)2],
∴这组数据的平均数是6,数据个数是4,
∴这组数据的总和为4×6=24;
故答案为:24.
15.(3分)多项式x2+mx+6因式分解得(x﹣2)(x+n),则m= ﹣5 .
【分析】根据因式分解是把一个多项式转化成几个整式积,可得答案.
【解答】解:x2+mx+6因式分解得(x﹣2)(x+n),得
x2+mx+6=(x﹣2)(x+n),(x﹣2)(x+n)=x2+(n﹣2)x﹣2n,
x2+mx+6=x2+(n﹣2)x﹣2n,
﹣2n=6,m=n﹣2.
解得n=﹣3,m=﹣5,
故答案为:﹣5.
16.为响应国家“乡村旅游振兴”战略号召,几名同学准备参加“大美青海”旅游活动,包租一辆面包车从西宁前往青海湖.面包车的租价为240元,出发时又增加了4名同学,每人比原来少分担了10元车费.设原有人数为x人,则可列方程 ﹣=10 .
【分析】利用人均分担的费用=租车费用÷人数,结合又增加了4名同学后比原来少分担了每人10元车费,即可得出关于x的分式方程,此题得解.
【解答】解:依题意得:﹣=10.
故答案为:﹣=10.
17.在实数范围内分解因式:2x3﹣6x= 2x(x+)(x﹣) .
【分析】先提公因式,然后利用平方差公式分解.
【解答】解:原式=2x(x2﹣3)
=2x(x+)(x﹣).
故答案为
18.观察下列等式:,,,……计算的结果为 .
【分析】由所给式子可将所求式子化为:(﹣+﹣+﹣+﹣)即可求解.
【解答】解:=(﹣+﹣+﹣+﹣)=(﹣)=,
故答案为.
三、解答题:(本大题共7小题,共62分。解答要写出必要的文字说明,证明过程或演算步骤)
19.(1)20222﹣2021×2023 (用简便方法计算);
(2)解方程:=﹣2.
【分析】(1)根据平方差公式简化运算即可;
(2)根据解分式方程的步骤求解即可.
【解答】解:(1)20222﹣2021×2023
=20222﹣(2022﹣1)×(2022+1)
=20222﹣20222+1
=1;
(2)去分母,得2﹣x=﹣1﹣2(x﹣3),
解得x=3,
经检验,x=3是原方程的增根,
∴原方程无解.
20.(8分)化简求值:(﹣x+1)÷,其中x从0、2、﹣1中任意取一个数求值.
【分析】先算括号内的加减,把除法变成乘法,算乘法,最后代入求出答案即可.
【解答】解:(﹣x+1)÷
=
=
=﹣,
∵从分式知:x+1≠0,x﹣2≠0,
∴x≠﹣1且x≠2,
取x=0,
当x=0时,原式=﹣=1.
21.(10分)某校为调查学生对海洋科普知识的了解情况,从全校学生中随机抽取n名学生进行测试,测试成绩进行整理后分成五组,并绘制成如图的频数分布直方图和扇形统计图.
请根据图中信息解答下列问题:
(1)补全频数分布直方图;
(2)在扇形统计图中,“70~80”这组的百分比m= 20% ;
(3)已知“80~90”这组的数据如下:81,83,84,85,85,86,86,86,87,88,88,89.抽取的n名学生测试成绩的中位数是 84.5 分;
(4)若成绩达到80分以上(含80分)为优秀,请你估计全校1200名学生对海洋科普知识了解情况为优秀的学生人数.
【分析】(1)求出调查人数,和“90﹣100”的人数即可补全频数分布直方图;
(2)用“70﹣80”的频数10除以调查人数50 即可得出m的值;
(3)利用中位数的意义,求出中间位置的两个数的平均数,即可得出中位数;
(4)样本估计总体,样本中优秀所占的百分比为,因此估计总体1200人的是优秀的人数.
【解答】解:(1)8÷16%=50(人),50﹣4﹣8﹣10﹣12=16(人),补全频数分布直方图如图所示:
(2)m=10÷50=20%,
故答案为:20%;
(3)将50个数据从小到大排列后,处在第25、26位的两个数的平均数为=84.5,
因此中位数是84.5,
故答案为:84.5;
(4)1200×=672(人),
答:估计全校1200名学生对海洋科普知识了解情况为优秀的学生大约有672人.
22.(5分)(1)若=﹣恒成立,求A、B的值.
(2)已知a,b,c是△ABC三边的长度,且满足a2+2b2+c2﹣2b(a+c)=0,求△ABC的形状.
【分析】(1)先把等式右边通分,再根据多项式相等,对应项的系数相等,列方程求解;
(2)先把等号左边配方,再根据平方的非负性求解.
【解答】解:(1)∵=﹣=,
∴2x+3=Ax+2A﹣Bx﹣B=(A﹣B)x+(2A﹣B),
∴A﹣B=2且2A﹣B=3,
解得:A=1,B=﹣1;
(2)∵a2+2b2+c2﹣2b(a+c)
=a2+2b2+c2﹣2ba﹣2bc
=(a﹣b)2+(b﹣c)2=0,
∴a=b=c,
∴△ABC的形状为等边三角形.
23.(6分)轮船在顺水中航行30千米的时间与在逆水中航行20千米所用的时间相等,已知水流速度为2千米/时,求船在静水中的速度.
【分析】设船在静水中的速度是x千米/小时,根据轮船在顺水中航行30千米的时间与在逆水中航行20千米所用的时间相等,已知水流速度为2千米/小时,可列方程求解.
【解答】解:设船在静水中的速度是x千米/小时,
根据题意得,=,
x=10,
经检验x=10是分式方程的解.
所以船在静水中的速度是10千米/小时.
24.(10分)某工程项目拟由甲、乙两个工程队共同完成.已知甲工程队的工作效率是乙工程队工作效率的1.5倍,且两个工程队合做24天恰好完成该工程任务.
(1)甲、乙两个工程队单独完成该工程项目各需多少天?
(2)若甲、乙两个工程队每天的施工费用分别为0.6万元和0.35万元,要使该工程项目总的施工费用不超过22万元,则乙工程队至少需要施工多少天?
【分析】(1)设甲工程队单独完成此项目需x天,乙工程队单独完成此项目需y天.由题意:甲工程队的工作效率是乙工程队工作效率的1.5倍,且两个工程队合做24天恰好完成该工程任务.列出分式方程组,解分式方程组即可;
(2)设甲工程队施工a天,乙工程队施工b天时,由甲、乙两队的工作量之和为1及总费用不超过22万元两个关系进行分析即可.
【解答】解:(1)设甲工程队单独完成此项目需x天,乙工程队单独完成此项目需y天.
依题意得:,
解得:,
经检验,是原方程组的解,且符合题意.
答:甲工程队单独完成此项目需40天,乙工程队单独完成此项目需60天.
(2)设甲工程队施工a天,乙工程队施工b天时,总的施工费用不超过22万元.
根据题意得:,
解得:b≥40.
答:要使该项目总的施工费用不超过22万元,乙工程队最少施工40天.
25.(10分)[阅读材料]
因式分解:(x+y)2+2(x+y)+1.
解:将“x+y”看成整体,令x+y=A,则原式=A2+2A+1=(A+1)2.
再将“A”还原,原式=(x+y+1)2.
上述解题用到的是“整体思想”,整体思想是数学解题中常用的一种思想方法.
[问题解决]
(1)因式分解:1+4(x﹣y)+4(x﹣y)2;
(2)因式分解:(x2﹣6x)(x2﹣6x+18)+81;
(3)证明:若n为正整数,则代数式(n+1)(n+2)(n2+3n)+1的值一定是某个整数的平方.
【分析】(1)用换元法设x﹣y=A,将原式化为1+4Α+4Α2,再利用完全平方公式得出(1+2A)2,再将A 还原即可;
(2)设 x2﹣6x=B,则原式=B(B+18)+81=B2+18B+81=(B+9)2后,再将B还原后,最后再利用完全平方公式即可;
(3)先计算(n+1)(n+2)=n2+3n+2,再利用完全平方公式即可.
【解答】解:(1)令x﹣y=A,
原式=1+4Α+4Α2
=(1+2A)2
=(1+2x﹣2y)2;
(2)令 a2﹣4a=B,
则原式=B(B+18)+81
=B2+18B+81
=(B+9)2
=(x2﹣6x+9)2
=(x﹣3)4;
(3)证明:原式=(n2+3n+2)(n2+3n)+1
=(n2+3n)2+2(n2+3n)+1
=(n2+3n+1)2,
∵n为正整数,
∴n2+3n+1为正整数.
∴(n+1)(n+2)(n2+3n)=(n2+3n+1)2,
即代数(n+1)(n+2)(n2+3n)+1的值一定是某个整数的平方.
同课章节目录
