双曲线[上学期]
图片预览






文档简介
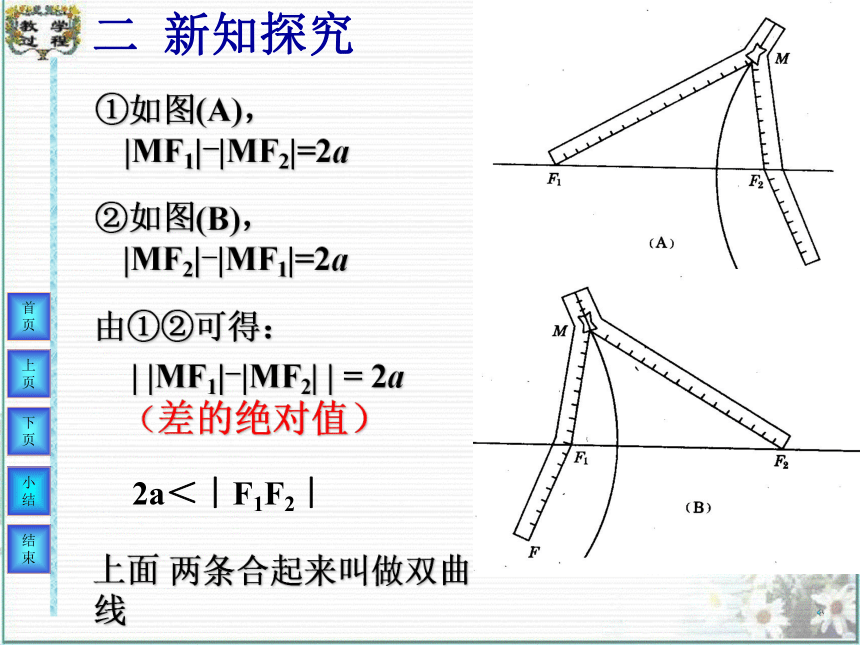
课件24张PPT。1. 椭圆的定义2. 引入问题:动画①如图(A), |MF1|-|MF2|=2a②如图(B),|MF2|-|MF1|=2a上面 两条合起来叫做双曲线由①②可得: | |MF1|-|MF2| | = 2a
(差的绝对值)2a<︱F1F2︱二 新知探究学习目标 掌握双曲线定义。
能利用双曲线定义解有关问题。
掌握双曲线标准方程。
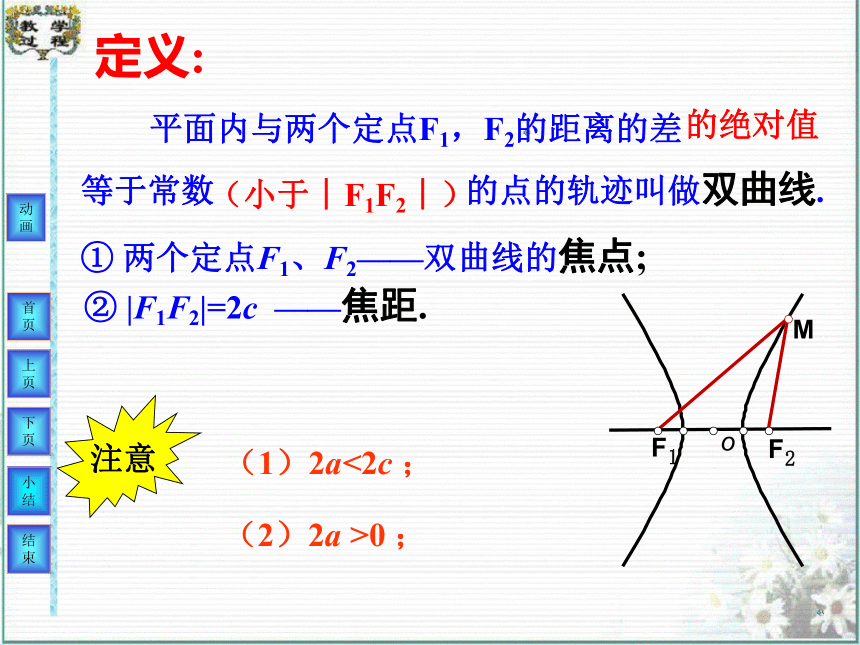
4 能根据所给条件求双曲线标准方程。① 两个定点F1、F2——双曲线的焦点;② |F1F2|=2c ——焦距.(1)2a<2c ; 平面内与两个定点F1,F2的距离的差等于常数 的点的轨迹叫做双曲线.(2)2a >0 ;动画的绝对值(小于︱F1F2︱)注意定义:动点M的轨迹探究
(F1、F2是两定点, |F1F2| =2c (a,c为正常数)
当|MF1|-|MF2|=2a时a 当|MF2|-|MF1|=2a时a 当a=c时,动点M的轨迹 ;
当a>c时,动点M的轨迹 .
因此,在应用定义时,首先要考查 .双曲线的右支双曲线的左支以F1、F2为端点的两条射线不存在2a与2c的大小线段F1F2的垂直平分线F1F2当a=0时,动点M的是轨迹_______________________. 1. 建系设点.2. 写出适合条件的点M的集合;3. 用坐标表示条件,列出方程;4. 化简.求曲线方程的步骤:方程的推导方程的推导设M(x,y) F1(-c,0)F2(c,0)则
︱︱MF1︱-︱MF2︱︱=2a∴︱√(x+c)2+y2-√(x-c)2+y2︱=2a√(x+c)2+y2-√(x-c)2+y2=2a或√(x+c)2+y2-√(x-c)2+y2=-2a整理有 (c2-a2)x2-a2y=a2(c2-a2)令c2-a2=b2(b>0)则有
b2x2-a2y2=a2b2x2
a2
y2
b2-=1∴双曲线的标准方程问题:如何判断双曲线的焦点在哪个轴上?规律:椭圆看大小,双曲线看符号例1:指出以下双曲线的a、b、c、焦点坐标F(±5,0)F(0,±5)三 知识运用与解题研究例2、已知双曲线的焦点为F1(-5,0), F2(5,0)双曲线上一点到焦点的距离差的绝对值等于6,则
(1) a=_______ , c =_______ , b =_______
(2) 双曲线的标准方程为______________(3)双曲线上一点P, |PF1|=10,
则|PF2|=_________3544或16点拔:双曲线的定义蕴含了方程思想。(已知两个可求另一个)例3 已知双曲线的焦点为F1(-5,0),F2(5,0),双曲线上
一点P到F1、F2的距离的差的绝对值等于6,求双曲线
的标准方程.∵ 2a = 6, c=5∴ a = 3, c = 5∴ b2 = 52-32 =16所以所求双曲线的标准方程为:1、已知点F1(- 8, 3 )、F2(2 ,3),动点P满足
|PF1| - |PF2|= 10,则P点的轨迹是( ) A、双曲线 B、双曲线一支
C、直线 D、一条射线2、若椭圆 与双曲线
的焦点相同,则 a = 3D3、若双曲线 的焦距为6,则m= 6或-6四 练习巩固练习4:如果方程 表示双曲线,
求m的取值范围.分析:方程 表示双曲线时,则m的取值
范围_________________.变式一:分析:上题的椭圆与双曲线的一个交点为P,
焦点为F1,F2,求|PF1|.变式:|PF1|+|PF2|=10,分析:思考1:说明下列方程各表示什么曲线。方程表示的曲线是双曲线方程表示的曲线是双曲线的右支方程表示的曲线是x轴上分别以F1和F2为端点,
指向x轴的负半轴和正半轴的两条射线。思考2:已知方程kx2+y2=4(k∈R),讨
论k取不同实数时方程所表示的曲线.(1) K=0时,直线y=±2.
(2) k=1时,是x2+y2=4,圆.
(3)0(4) k>1时,是焦点在y轴上的椭圆.
(5)k<0时,焦点在y 轴上的双曲线.| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)F ( ±c, 0) F(0, ± c)小结五F(±c,0)F(±c,0)a>0,b>0,但a不一定大于b,c2=a2+b2a>b>0,a2=b2+c2双曲线与椭圆之间的区别与联系:||MF1|-|MF2||=2a |MF1|+|MF2|=2a F(0,±c)F(0,±c)祝同学们身体健康,学习进步,天 天 好 心 情!
(差的绝对值)2a<︱F1F2︱二 新知探究学习目标 掌握双曲线定义。
能利用双曲线定义解有关问题。
掌握双曲线标准方程。
4 能根据所给条件求双曲线标准方程。① 两个定点F1、F2——双曲线的焦点;② |F1F2|=2c ——焦距.(1)2a<2c ; 平面内与两个定点F1,F2的距离的差等于常数 的点的轨迹叫做双曲线.(2)2a >0 ;动画的绝对值(小于︱F1F2︱)注意定义:动点M的轨迹探究
(F1、F2是两定点, |F1F2| =2c (a,c为正常数)
当|MF1|-|MF2|=2a时a
当a>c时,动点M的轨迹 .
因此,在应用定义时,首先要考查 .双曲线的右支双曲线的左支以F1、F2为端点的两条射线不存在2a与2c的大小线段F1F2的垂直平分线F1F2当a=0时,动点M的是轨迹_______________________. 1. 建系设点.2. 写出适合条件的点M的集合;3. 用坐标表示条件,列出方程;4. 化简.求曲线方程的步骤:方程的推导方程的推导设M(x,y) F1(-c,0)F2(c,0)则
︱︱MF1︱-︱MF2︱︱=2a∴︱√(x+c)2+y2-√(x-c)2+y2︱=2a√(x+c)2+y2-√(x-c)2+y2=2a或√(x+c)2+y2-√(x-c)2+y2=-2a整理有 (c2-a2)x2-a2y=a2(c2-a2)令c2-a2=b2(b>0)则有
b2x2-a2y2=a2b2x2
a2
y2
b2-=1∴双曲线的标准方程问题:如何判断双曲线的焦点在哪个轴上?规律:椭圆看大小,双曲线看符号例1:指出以下双曲线的a、b、c、焦点坐标F(±5,0)F(0,±5)三 知识运用与解题研究例2、已知双曲线的焦点为F1(-5,0), F2(5,0)双曲线上一点到焦点的距离差的绝对值等于6,则
(1) a=_______ , c =_______ , b =_______
(2) 双曲线的标准方程为______________(3)双曲线上一点P, |PF1|=10,
则|PF2|=_________3544或16点拔:双曲线的定义蕴含了方程思想。(已知两个可求另一个)例3 已知双曲线的焦点为F1(-5,0),F2(5,0),双曲线上
一点P到F1、F2的距离的差的绝对值等于6,求双曲线
的标准方程.∵ 2a = 6, c=5∴ a = 3, c = 5∴ b2 = 52-32 =16所以所求双曲线的标准方程为:1、已知点F1(- 8, 3 )、F2(2 ,3),动点P满足
|PF1| - |PF2|= 10,则P点的轨迹是( ) A、双曲线 B、双曲线一支
C、直线 D、一条射线2、若椭圆 与双曲线
的焦点相同,则 a = 3D3、若双曲线 的焦距为6,则m= 6或-6四 练习巩固练习4:如果方程 表示双曲线,
求m的取值范围.分析:方程 表示双曲线时,则m的取值
范围_________________.变式一:分析:上题的椭圆与双曲线的一个交点为P,
焦点为F1,F2,求|PF1|.变式:|PF1|+|PF2|=10,分析:思考1:说明下列方程各表示什么曲线。方程表示的曲线是双曲线方程表示的曲线是双曲线的右支方程表示的曲线是x轴上分别以F1和F2为端点,
指向x轴的负半轴和正半轴的两条射线。思考2:已知方程kx2+y2=4(k∈R),讨
论k取不同实数时方程所表示的曲线.(1) K=0时,直线y=±2.
(2) k=1时,是x2+y2=4,圆.
(3)0
(5)k<0时,焦点在y 轴上的双曲线.| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)F ( ±c, 0) F(0, ± c)小结五F(±c,0)F(±c,0)a>0,b>0,但a不一定大于b,c2=a2+b2a>b>0,a2=b2+c2双曲线与椭圆之间的区别与联系:||MF1|-|MF2||=2a |MF1|+|MF2|=2a F(0,±c)F(0,±c)祝同学们身体健康,学习进步,天 天 好 心 情!
