双曲线、抛物线[下学期]
图片预览




文档简介
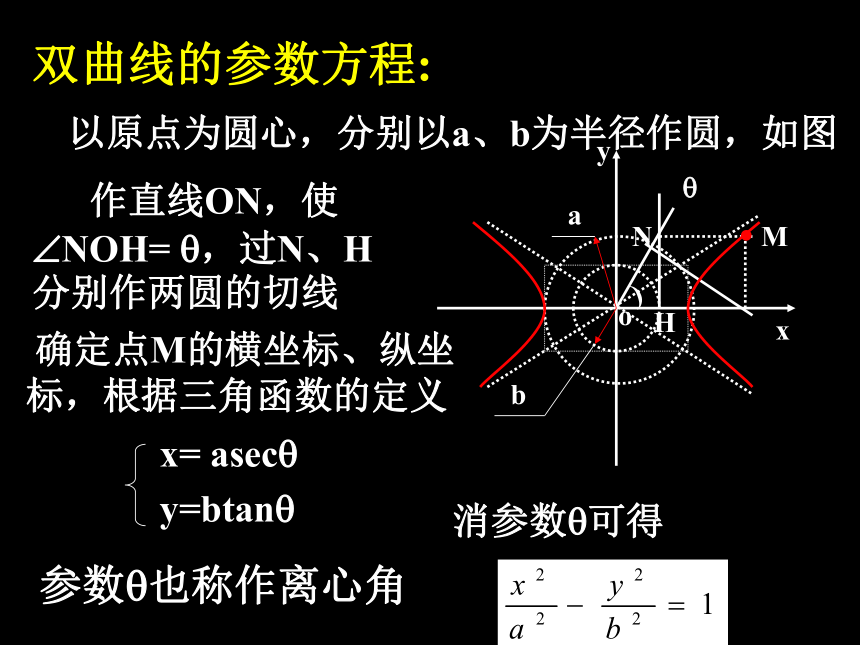
课件12张PPT。?baoxy?)MHN双曲线的参数方程: 以原点为圆心,分别以a、b为半径作圆,如图 作直线ON,使?NOH= ?,过N、H分别作两圆的切线
确定点M的横坐标、纵坐标,根据三角函数的定义
x= asec?
y=btan?
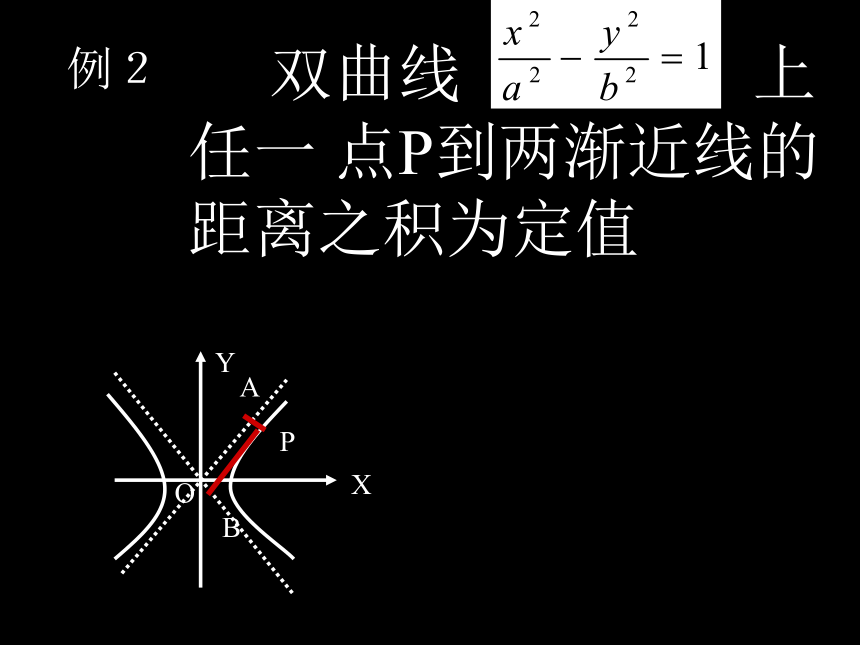
参数?也称作离心角消参数?可得 双曲线 上任一 点P到两渐近线的距离之积为定值XYOPAB例2问题1 上题中,若AP 、BP分 别与
渐近线平行 ,问
为定值吗?BPAO问题2 四边形PAOB 的面积为
定值.BPAOXY抛物线的参数方程:
抛物线 y2=2px (p>0)
化参数方程
设M(x,y)为抛物线上
任一点,x = — ,?MOH= ?
ctg?= —— = — ?y=2pcot?,令cot? = t
抛物线y2=2px的参数方程是
x= 2pt2
y= 2pt
oyx?)HM(x,y)y22py—y22p2pyt是参数,抛物线上的点可表示为(2pt2,2pt)引伸2:P、Q是抛物线y2 = x与圆 (x-3)2+y2=1上的两动点,求PQ的最小值xyAPQ引伸3 点P在椭圆 上运
动,点Q在圆 上运动,求PQ的最
大值XYPQOA例2 过抛物线 (t为参数,p>0)的焦点作倾斜角为θ的直线交抛物线于A、B两点,设0<θ<π,当θ取什么值时,|AB|取最小值。引伸1 : 点P在椭圆
的第一象限的那一段上,求四边形PAOB的面积最大值yABOPx 例3 点P在椭圆 上运动,直线x+2y-2=0交椭圆于点A、B,问P处于何处时,P到直线的距离最大?xyABOP
圆锥曲线参数方程一用来证明定值问题、定点问题 有关等式问题,避免复杂的
消去参数的过程 .小结 :
恰当应用圆锥曲线参数方程解题的优点:
1 容易建立函数
2 变量少,参数范围易得
3 简化消参过程
确定点M的横坐标、纵坐标,根据三角函数的定义
x= asec?
y=btan?
参数?也称作离心角消参数?可得 双曲线 上任一 点P到两渐近线的距离之积为定值XYOPAB例2问题1 上题中,若AP 、BP分 别与
渐近线平行 ,问
为定值吗?BPAO问题2 四边形PAOB 的面积为
定值.BPAOXY抛物线的参数方程:
抛物线 y2=2px (p>0)
化参数方程
设M(x,y)为抛物线上
任一点,x = — ,?MOH= ?
ctg?= —— = — ?y=2pcot?,令cot? = t
抛物线y2=2px的参数方程是
x= 2pt2
y= 2pt
oyx?)HM(x,y)y22py—y22p2pyt是参数,抛物线上的点可表示为(2pt2,2pt)引伸2:P、Q是抛物线y2 = x与圆 (x-3)2+y2=1上的两动点,求PQ的最小值xyAPQ引伸3 点P在椭圆 上运
动,点Q在圆 上运动,求PQ的最
大值XYPQOA例2 过抛物线 (t为参数,p>0)的焦点作倾斜角为θ的直线交抛物线于A、B两点,设0<θ<π,当θ取什么值时,|AB|取最小值。引伸1 : 点P在椭圆
的第一象限的那一段上,求四边形PAOB的面积最大值yABOPx 例3 点P在椭圆 上运动,直线x+2y-2=0交椭圆于点A、B,问P处于何处时,P到直线的距离最大?xyABOP
圆锥曲线参数方程一用来证明定值问题、定点问题 有关等式问题,避免复杂的
消去参数的过程 .小结 :
恰当应用圆锥曲线参数方程解题的优点:
1 容易建立函数
2 变量少,参数范围易得
3 简化消参过程
