苏科版初中数学九年级下册 6.1 图上距离与实际距离 课件(共22张PPT)
文档属性
| 名称 | 苏科版初中数学九年级下册 6.1 图上距离与实际距离 课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 560.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-29 14:49:35 | ||
图片预览






文档简介
(共22张PPT)
6.1 图上距离与实际距离
“宇宙之大,粒子之微,火箭之速,地球之变,生物之迷,日用之繁”无一能离开数学。
——华罗庚
图片欣赏
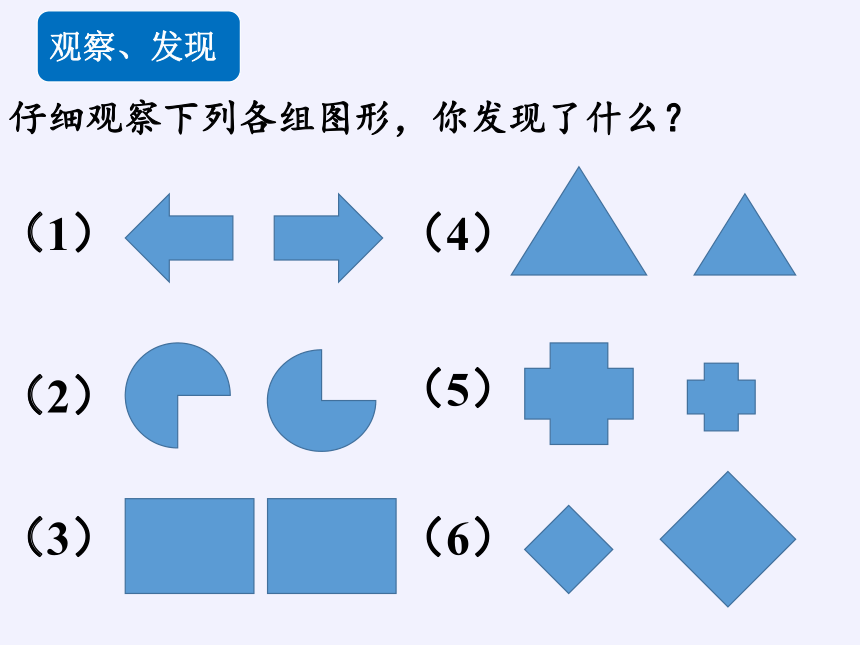
仔细观察下列各组图形,你发现了什么?
(1)
(3)
(2)
(4)
(5)
(6)
观察、发现
同一张底片印出来的不同大小照片
图片欣赏
商场里各种大小的电视机画面
图片欣赏
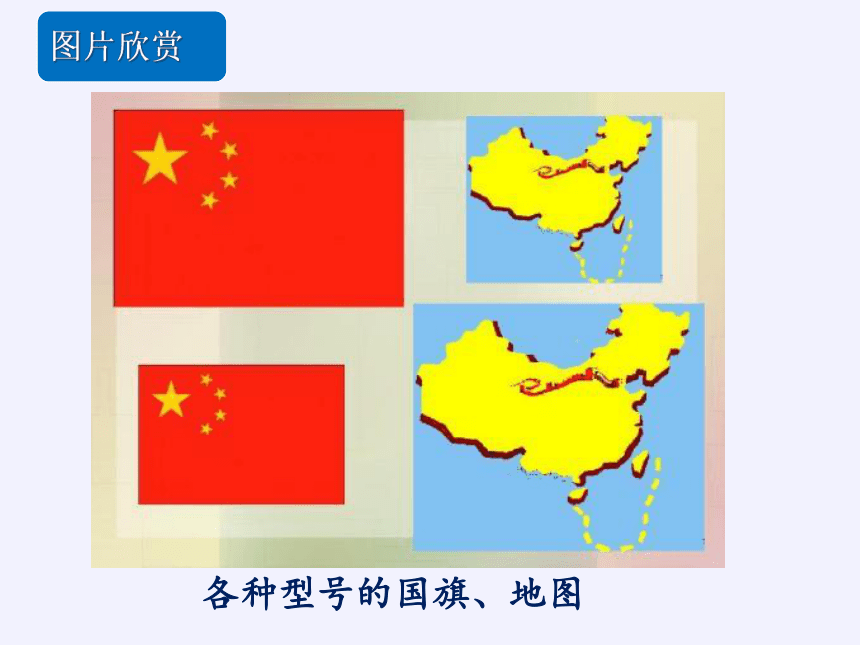
各种型号的国旗、地图
图片欣赏
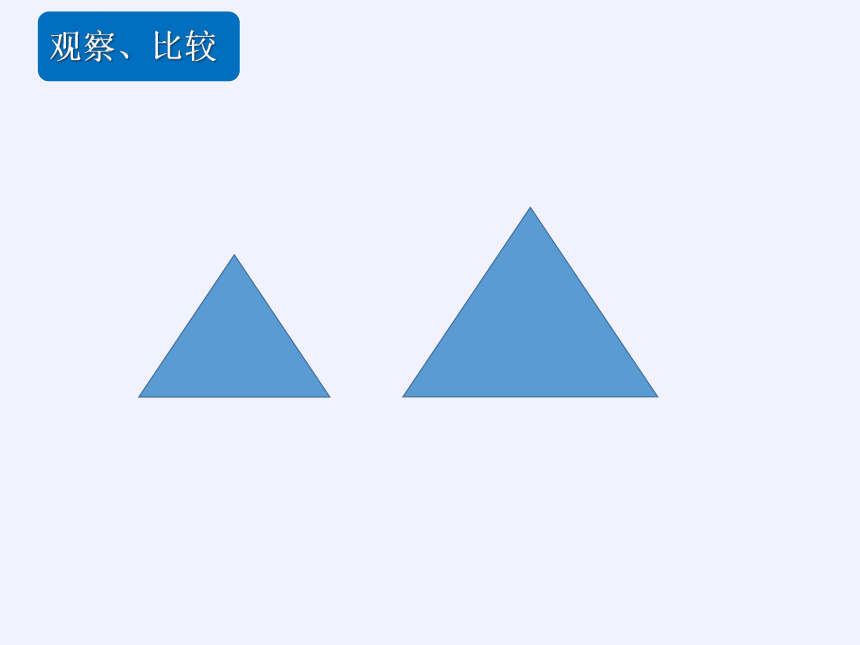
观察、比较
新知探求
在四条线段中,如果两条线段的比等于另两条线段的比,那么这四条线段叫做成比例线段.
例如:
线段a,b,c,d满足a:b=c:d,那么线段a,b,c,d是成比例线段.
比例的基本性质:
如果a :b=c :d,那么ad=bc;反过来,
如果ad=bc(b ≠0, d ≠0),那么a :b=c :d.
在比例式a :b=b :c中,b叫做a和c的比例中项.
新知探求
1. 下列矩形中,哪两个矩形的长和宽是成比例线段?
4
6
6
8
6
9
(1)
(2)
(3)
思考与探索
2.如图,线段A1B1、B1C1、A2B2、B2C2的端点都在边长为1的小正方形的顶点上.这四条线段是成比例线段吗?为什么?
思考与探索
例1 .某公园平面图上有一块三角形草地,测得三边长分别为4cm、5cm、6cm,已知这块三角形草地地最短边实际长度为80m,求另两条边的实际长度.
例题讲解
三角形草地的另两条边的实际距离分别为:
5×2000=10000(cm)=100m
6×2000=12000(cm)=120m
答:三角形草地的另两条边的实际距离分别
为100m和120m.
解:比例尺=图上距离:实际距离=4:8000=1:2000.
例题讲解
例2.已知
全等三角形的性质 相似三角形的性质
对应角相等 ?
对应边相等 ?
探索、猜想
F
E
D
B
A
C
三角形全等的条件 三角形相似的条件
两边分别相等并且夹角相等 ?
两角分别相等并且夹边相等
两角分别相等并且一角的对边相等
三边分别相等
探索、猜想
全等图形可以通过图形的变换得到,那么相似呢?
(1)
(2)
(3)
(4)
探索、猜想
位似图形
通过本堂课的研究和学习,你能回答的出这三个问题吗?
为什么学?—学什么?—怎么学?
反思、小结
作业
完成书上p42 习题6.1
给我最大快乐的,不是已懂得知识,而是不断的学习;不是已有的东西,而是不断的获取;不是已达到的高度,而是继续不断的攀登。 ——高斯
谢 谢
6.1 图上距离与实际距离
“宇宙之大,粒子之微,火箭之速,地球之变,生物之迷,日用之繁”无一能离开数学。
——华罗庚
图片欣赏
仔细观察下列各组图形,你发现了什么?
(1)
(3)
(2)
(4)
(5)
(6)
观察、发现
同一张底片印出来的不同大小照片
图片欣赏
商场里各种大小的电视机画面
图片欣赏
各种型号的国旗、地图
图片欣赏
观察、比较
新知探求
在四条线段中,如果两条线段的比等于另两条线段的比,那么这四条线段叫做成比例线段.
例如:
线段a,b,c,d满足a:b=c:d,那么线段a,b,c,d是成比例线段.
比例的基本性质:
如果a :b=c :d,那么ad=bc;反过来,
如果ad=bc(b ≠0, d ≠0),那么a :b=c :d.
在比例式a :b=b :c中,b叫做a和c的比例中项.
新知探求
1. 下列矩形中,哪两个矩形的长和宽是成比例线段?
4
6
6
8
6
9
(1)
(2)
(3)
思考与探索
2.如图,线段A1B1、B1C1、A2B2、B2C2的端点都在边长为1的小正方形的顶点上.这四条线段是成比例线段吗?为什么?
思考与探索
例1 .某公园平面图上有一块三角形草地,测得三边长分别为4cm、5cm、6cm,已知这块三角形草地地最短边实际长度为80m,求另两条边的实际长度.
例题讲解
三角形草地的另两条边的实际距离分别为:
5×2000=10000(cm)=100m
6×2000=12000(cm)=120m
答:三角形草地的另两条边的实际距离分别
为100m和120m.
解:比例尺=图上距离:实际距离=4:8000=1:2000.
例题讲解
例2.已知
全等三角形的性质 相似三角形的性质
对应角相等 ?
对应边相等 ?
探索、猜想
F
E
D
B
A
C
三角形全等的条件 三角形相似的条件
两边分别相等并且夹角相等 ?
两角分别相等并且夹边相等
两角分别相等并且一角的对边相等
三边分别相等
探索、猜想
全等图形可以通过图形的变换得到,那么相似呢?
(1)
(2)
(3)
(4)
探索、猜想
位似图形
通过本堂课的研究和学习,你能回答的出这三个问题吗?
为什么学?—学什么?—怎么学?
反思、小结
作业
完成书上p42 习题6.1
给我最大快乐的,不是已懂得知识,而是不断的学习;不是已有的东西,而是不断的获取;不是已达到的高度,而是继续不断的攀登。 ——高斯
谢 谢
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
