苏科版九年级下册第5章 二次函数 复习课件(共26张PPT)
文档属性
| 名称 | 苏科版九年级下册第5章 二次函数 复习课件(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 454.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-29 22:02:26 | ||
图片预览




文档简介
(共26张PPT)
第5章 二次函数 复习课件
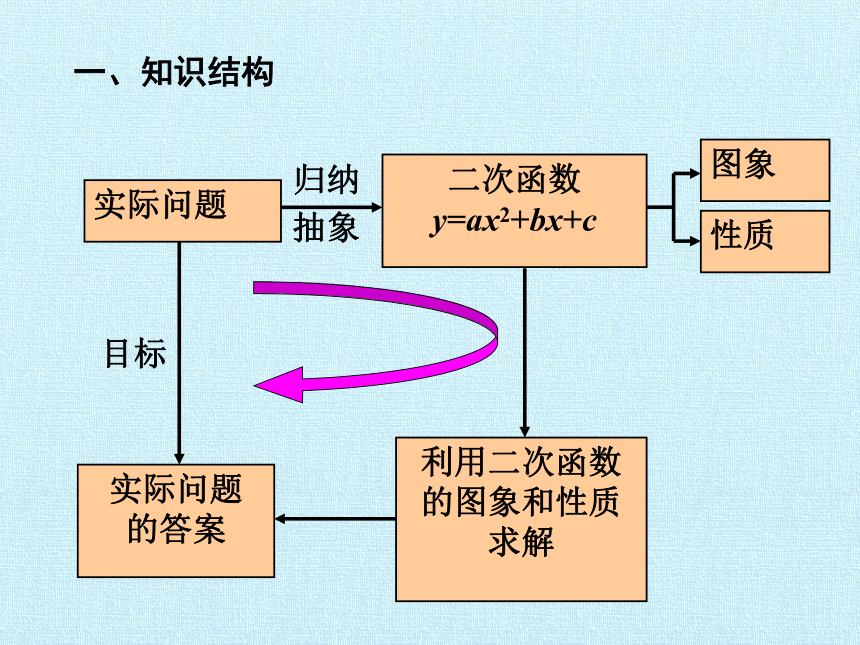
一、知识结构
实际问题
二次函数
y=ax2+bx+c
图象
性质
归纳
抽象
实际问题
的答案
利用二次函数的图象和性质求解
目标
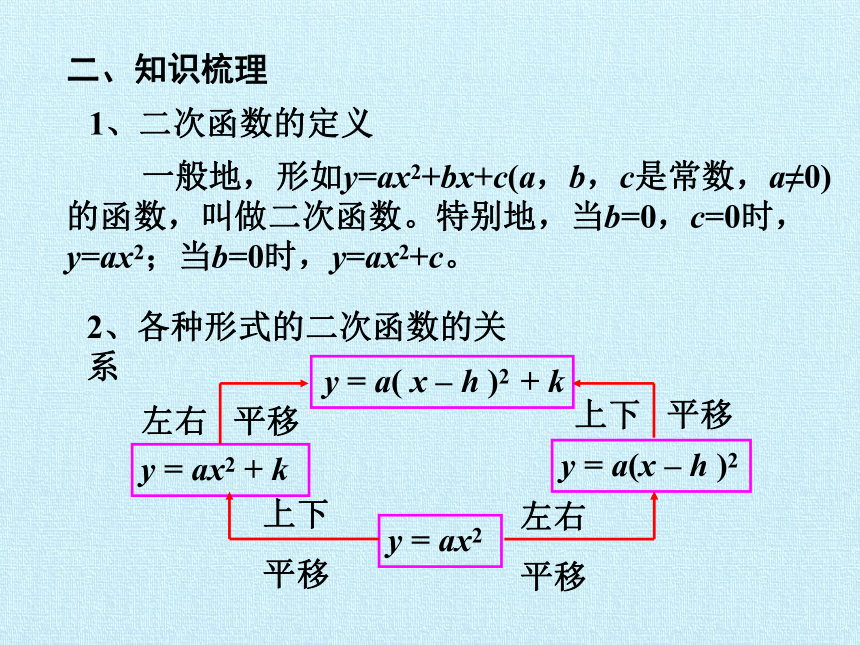
二、知识梳理
一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数,叫做二次函数。特别地,当b=0,c=0时,y=ax2;当b=0时,y=ax2+c。
1、二次函数的定义
y = ax2
y = ax2 + k
y = a(x – h )2
y = a( x – h )2 + k
上下
平移
上下 平移
2、各种形式的二次函数的关系
左右
平移
左右 平移
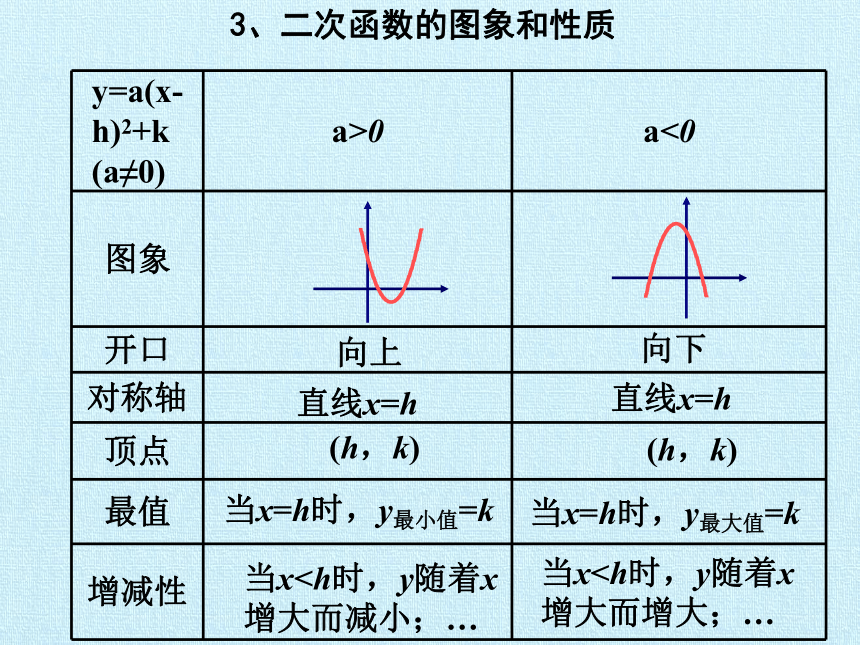
y=a(x-h)2+k (a≠0) a>0 a<0
图象
开口
对称轴
顶点
最值
增减性
向上
向下
直线x=h
直线x=h
(h,k)
(h,k)
当x=h时,y最小值=k
当x=h时,y最大值=k
当x当x3、二次函数的图象和性质
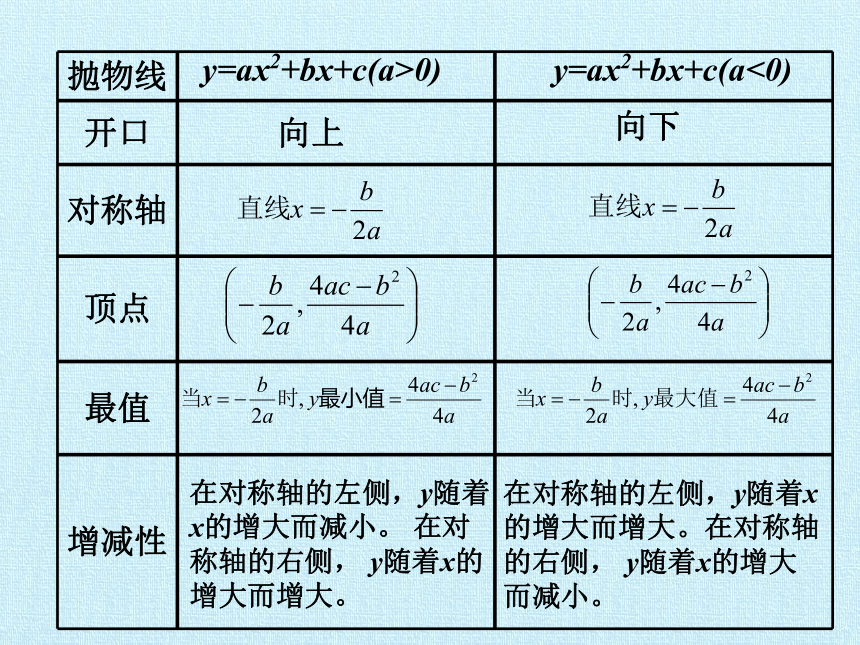
抛物线
开口
对称轴
顶点
最值
增减性
y=ax2+bx+c(a>0)
y=ax2+bx+c(a<0)
向上
向下
在对称轴的左侧,y随着x的增大而减小。 在对称轴的右侧, y随着x的增大而增大。
在对称轴的左侧,y随着x的增大而增大。在对称轴的右侧, y随着x的增大而减小。
4、二次函数 y=ax2+bx+c 的图象和x轴交点的三种情况与一元二次方程根的关系:
二次函数y=ax2+bx+c的图象和x轴交点 一元二次方程ax2+bx+c= 0的根 一元二次方程ax2+bx+c= 0根的判别式Δ=b2-4ac
有两个交点
有两个不等的实数根
只有一个交点(顶点)
有两个相等的实数根
没有交点
没有实数根
b2 – 4ac > 0
b2 – 4ac = 0
b2 – 4ac < 0
(1)关键是求出待定系数____________的值。
(2)设解析式的三种形式:
①一般式:______________,当已知抛物线上三个点时,用一般式比较简便;
②顶点式:______________ ,当已知抛物线的顶点时,用顶点式较方便;
③交点式(两根式):__________________,当已知抛物线与 x 轴的交点坐标(x1,0),(x2,0)时,用交点式较方便。
a,b,c
y=ax2+bx+c
y=a(x-h)2+k
y=a(x-x1)(x-x2)
5、求二次函数 y=ax +bx+c 的解析式
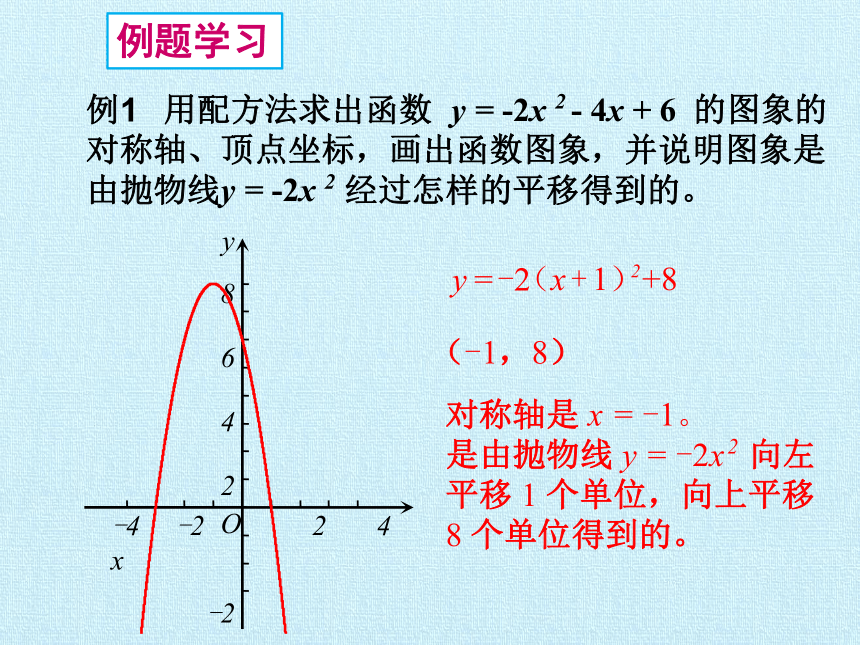
例1 用配方法求出函数 y = -2x 2 - 4x + 6 的图象的对称轴、顶点坐标,画出函数图象,并说明图象是由抛物线y = -2x 2 经过怎样的平移得到的。
(-1,8)
(x + 1)+8
2
y = -2
对称轴是 x = -1。
是由抛物线 y = -2x 2 向左
平移 1 个单位,向上平移
8 个单位得到的。
y
8
6
4
2
-2
-4 -2 2 4 x
O
例题学习
例2
已知二次函数
(1)求抛物线开口方向,对称轴和顶点M的坐标;(2)设抛物线与y轴交于C点,与x轴交于A、B两点求C,A,B的坐标;
(3)x为何值时,y随x的增大而减少,x为何值时,y有最大(小)值,这个最大(小)值是多少?
(4)x为何值时,y<0?x为何值时,y>0?
例3 根据下列条件,求出二次函数的解析式。
图象经过(-1,1),(1,3),(0,1)三点;
(2)图象的顶点为(-1,-8),且过点(0,-6);
(x + 1)-8
2
y = 2
例4:某商场购进一批单价为16元的日用品,经实
验发现若按每件20元的价格销售时,每月能卖360
件,若按每件25元的价格销售时,每月能卖210件,假设每月销售件数为y(件)是价格x(元/件)的一次函数。
(1)试求y与x之间的函数关系式。
(2)在商品不积压,且不考虑其他因素的条件下,问:销售价格定为每件多少时,才能使每月获得最大利润?每月的最大利润是多少?
解:
(1)y=kx+b
把x=20时,y=360;x=25时,y=210分别代入上式
得 :
360=20k+b 210=25k+b
解得:
k=30,b=960
所以y与x之间的函数关系式为y=-30x+960(x≥16,且x为整数)
(2)设每月利润为P元,
P=y(x-16)=(30x+960)(x-16)
=-30x +1440x-15360
P为最大值:(-30×24+960)(24-16)=1920(元)
答:当销售价格为每件24元时,每月利润最大,最大利润为1920元。
应用训练
1.在二次函数y=ax2+bx+c中,ac >0,则它的图像与x轴的关系是( )
A. 没有交点 B. 有两个交点
C. 有一个交点 D. 不能确定
B
2.已知抛物线y=x2+px+q经过点(5,0),(-5,0),则 p+q=( )
A. 0 B. 25 C. -25 D. 5
C
3.若二次函数 y=ax2 +bx+c 的图象如下,与x轴的一个交点为(1,0),则下列各式中不成立的是( )
A. b2-4ac>0 B. abc>0
C. a+b+c=0 D. a-b+c<0
1
x
y
o
-1
B
4.方程x2-3x=0的两根是x1=0,x2=3,抛物线
与x轴交点坐标是 ( )
A. (0,0) (3,0) B. (0,0) (0,3)
C. (0,0) (-3,0) D. (0,0) (0,-3)
A
一、选择题
C
5.二次函数y=x2-x-2的图象如图所示,则函数值y<0时x的取值范围是( )
(A). x<-1 (B) x>2
(C). -1<x<2 (D) x<-1或x>2
x
y
o
-1
2
6.如图,两条抛物线y1= - x2+1,y2= - x2-1与分别经过点(-2,0),(2,0)且平行于y轴的两条平行线围成的阴影部分的面积为( )
(A)8 (B)6 (C)10 (D)4
2
1
2
1
A
7.如图,点A,B的坐标分别为(1, 4)和(4, 4),抛物线y=a(x-m)2+n的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为( )
(A)-3 (B)1 (C)5 (D)8
x
y
o
A(1,4)
B(4,4)
C
D
D
1.已知二次函数y=x2+mx+2的图像与x轴的一个交点是(2,0),则与x轴另一个交点_______,m=_________。
(1,0)
-3
二、填空题
2.当m______时,抛物线y=4x2-4x+m与x轴只有一个交点,交点是________。
=1
( ,0)
2
1
3. 若二次函数y=kx2+3x-5的图像与x轴有两个交点,则k的取值范围是__________________。
k>- 且k≠0
20
9
4.如果关于x的一元二次方程 x2-2x+m=0有两个相等的实数根,则m=_,此时抛物线 y=x2-2x+m与x轴有__个交点。
1
1
5.已知实数x,y满足x2+3x+y-3=0,则x+y的最大值为_____。
4
6.已知二次函数y=ax2+bx+c的图像如图,用不等式连结下列各式:a __0,b __0,c ___0,
b2-4ac___0 a+b+c___0,a-b+c___0。
>
>
>
>
<
<
1
-1
x
y
o
7.若二次函数y=-x2+2x+k的部分图象如图所示,关于x的一元二次方程-x2+2x+k=0的一个解x1=3,另一个解x2=_____。
-1
8.已知二次函数的图象的顶点坐标为(-2,-3),且图象过点(-3,-2),则此二次函数的解析式 ;设此二次函数的图象与x轴交于A,B两点,O为坐标原点,则线段OA,OB的长度之和是 。
9.某商场将进价40元一个的某种商品按50元一个售出时,能卖出500个,已知这种商品每个涨价1元,销量减少10个,设每个涨价x元,销售价可以表示为 ,一个商品所获利润可以表示为 ,销售量可以表示为 ________,利润可以为 ,因此,定价是 元时,最大利润是 元。
(50+x)元
(50+x-40)元
(500-10x) 个
(50+x-40)(500-10x)
70
9000
10.不论x为何值时,函数y=ax2+bx+c(a≠0)的值永远为正的条件是____ _ 。
a>0, b -4ac<0
y=x2+4x+1
2√3
1.已知二次函数y=ax2+bx+c的最大值是2,图象顶点在直线y=x+1上,并且图象经过点(3,-6)。求a、b、c。
三、解答题:
∵二次函数的最大值是2∴抛物线的顶点纵坐标为2
顶点在直线y=x+1上
当y=2时,x=1。∴顶点坐标为( 1 , 2)
设解析式为y=a(x-1)2+2
∴a=-2 y=-2(x-1)2+2 y=-2x2+4x
2.已知抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同,顶点在直线x=1上,且顶点到x轴的距离为5,请写出满足此条件的抛物线的解析式。
a=1或a=-1
又∵顶点在直线x=1上,且顶点到x轴的距离为5,
顶点为(1,5)或(1,-5)
所以其解析式为:
(1) y=(x-1)2+5 (2) y=(x-1)2-5
(3) y=-(x-1)2+5 (4) y=-(x-1)2-5
3.已知二次函数y= x2+x-
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,
A,B的坐标。
(3)画出函数图象的示意图。
(4)求ΔMAB的周长及面积。
(5)x为何值时,y随x的增大而减小,x为何值时,y有最大
(小)值,这个最大(小)值是多少?
(6)x为何值时,y<0?x为何值时,y>0?
2
1
2
3
对称轴x=-1,顶点坐标M(-1,-2)
与x轴交点A(-3,0)B(1,0)C(0, )
2
3
图略
ΔMAB的周长=2MA+AB=2√2 ×2+4=4√2+4
ΔMAB的面积= AB×MD= ×4×2=4
2
1
2
1
当x<-1时,y随x的增大而减小;
当x=-1时,y最小值=-2
当x< -3或x>1时,y > 0
当-3 < x < 1时,y < 0
4.已知二次函数y=(x-2a)2+(a-1)(a为常数),当a取不同的值时,
其图像构成一个“抛物线系”。下图分别是a=-1,a=0,a=1,
a=2时二次函数的图像。它们的顶点在一直线上,
求这条直线的解析式。
x
y
O
a=-1
a=2
a=1
a=0
由题意知,
二次函数的顶点坐标是(2a,a-1)
代入各个a的值,即可得直线解析式
或设x=2a,y=a-1,消去a,即得:y= x-1
2
1
5.已知抛物线y=x2-2x-8,
(1)求证:该抛物线与x轴一定有两个交点;
(2)若该抛物线与x轴的两个交点分别为A、B,且它的顶点为P,求△ABP的面积。
x
y
o
A
P
B
△=22-4×(-8)=36>0
x2-2x-8=0
解方程得:x1=4, x2=-2
∴AB=4-(-2)=6 而P点坐标是(1,-9)
∴S△ABC=27
6、抛物线 y=-2x2+4x+6 顶点为A,与x轴交于B、C两点,与y轴交于D点,求四边形ABCD的面积。
y=-2x2+4x+6=-2(x-1)2+8,图像如图
A(1,8) B(-1,0) C(3,0) D(0,6)
3
-1
x
y
o
D
C
B
A
E
S四边形ABCD=SΔBOD+S梯形OEAD+SΔAEC
18
7.丁丁推铅球的出手高度为1.6m,如图所示,铅球的运行
路线近似为抛物线y=-0.1(x-k)2+2.5
①求k的值
②求铅球的落点与丁丁的距离。
③一个1.5m的小朋友跑到离原点6米的地方(如图),他会受到伤害吗?
x
y
O
B
(0,1.6)
①当x=0时,y=1.6
k=±3
对称轴是在y轴的右侧,即x=k>0,k=3
②-0.1(x-3)2+2.5=0得,x1 =8,x2 =-2所以,OB=8,故铅球的落点与丁丁的距离是8米。
③当x=6时,y=-0.1(6-3)2+2.5=1.6
>1.5
所以,这个小朋友不会受到伤害。
9、已知二次函数y=ax2-5x+c的图象如图。
(1) 当x为何值时,y随x的增大而增大;
(2) 当x为何值时,y<0;
(3)求它的解析式和顶点坐标。
(1)求k的取值范围;
(2)设抛物线与x轴交于A、B两点,且点A在点B的左侧,
点D是抛物线的顶点。如果△ABD是等腰直角三角形,求抛物线的解析式;
(3)在(2)的条件下,抛物线与y轴交于点C, 点E在y轴的正半轴上且以A、O、E为顶点的三角形与△AOC相似。求点E坐标。
2
1
8、已知抛物线y= x2-x+k 与x轴有两个交点。
10.某企业投资100万元引进一条产品加工生产线,若不计维修、保养费用,预计投产后每年可创利33万。该生产线投产后,从第1年到第x年的维修、保养费用累计为y(万元),且y=ax2+bx,若第1年的维修、保养 、费用为2万元,到第2年为6万元。
(1)求y的解析式;
(2)投产后,这个企业在第几年就能收回投资?
解:(1)由题意,x=1时,y=2;x=2时,y=2+4=6。分别代入y=ax2+bx,得a+b=2,4a+2b=6,
解得:a=1,b=1, ∴y=x2+x。
(2)设f=33x-100-x2-x,则
f=-x2+32x-100=-(x-16)2+156。
由于当1≤x≤16时,f随x的增大而增大,故当x=4时,即第4年可收回投资。
11.李明投资销售一种进价为每件20元的护眼台灯。销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=-10x+500。
(1)设李明每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(2)如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?(成本=进价×销售量)
(1)由题意,得:w=(x-20)·y=(x-20)·(-10x+500) =-10x2+700x-10 000
答:当销售单价定为35元时,每月可获得最大利润。
(2)由题意,得:-10x2+700x-10 000=2 000
解这个方程得:x1=30,x2=40。
答:李明想要每月获得2 000元的利润,销售单价应定为30元或40元。
(3)方法一:∵a=-10<0,∴抛物线开口向下。
∴当30≤x≤40时,w≥2 000。∵x≤32,∴当30≤x≤32时w≥2000。
设成本为P(元),由题意,得:
P=20×(-10x+500)=-200x+10 000
∵k=-200<0,∴P随x的增大而减小。
∴当x=32时,P最小=3600。
答:每月获得利润不低于2000元,每月成本最少为3600元。
方法二:∵a=-10<0,∴抛物线开口向下。
∴当30≤x≤40时,w≥2000。∵x≤32,∴30≤x≤32时,w≥2000。∵y=-10x+500,k=-10<0,∴y随x的增大而减小。∴当x=32时,y最小=180,
∵当进价一定时,销售量越小,成本越小,
∴20×180=3 600(元)
答:想要每月获得利润不低于2000元,每月成本最少为3600元。
12.用长为12 m的篱笆,一边利用足够长的墙围出一块苗圃。如图,围出的苗圃是五边形ABCDE,AE⊥AB,BC⊥AB,∠C=∠D=∠E。设CD=DE=x m,五边形ABCDE的面积为S m2问当x取什么值时,S最大?并求出S的最大值。
连结EC,作DF⊥EC,垂足为F。
∵∠DCB=∠CDE=∠DEA,
∠EAB=∠CBA=90°,
∴∠DCB=∠CDE=∠DEA=120°。
∵DE=CD,∴∠DEC=∠DCE=30°,
∴∠CEA=∠ECB=90°,
∴四边形EABC为矩形,又∵DE=x,
∴AE=6-x,DF= x,EC=√3x,
2
1
S= - x2+6√3x (03√3
4
当x=4m时,S最大=12√3m2
谢 谢
第5章 二次函数 复习课件
一、知识结构
实际问题
二次函数
y=ax2+bx+c
图象
性质
归纳
抽象
实际问题
的答案
利用二次函数的图象和性质求解
目标
二、知识梳理
一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数,叫做二次函数。特别地,当b=0,c=0时,y=ax2;当b=0时,y=ax2+c。
1、二次函数的定义
y = ax2
y = ax2 + k
y = a(x – h )2
y = a( x – h )2 + k
上下
平移
上下 平移
2、各种形式的二次函数的关系
左右
平移
左右 平移
y=a(x-h)2+k (a≠0) a>0 a<0
图象
开口
对称轴
顶点
最值
增减性
向上
向下
直线x=h
直线x=h
(h,k)
(h,k)
当x=h时,y最小值=k
当x=h时,y最大值=k
当x
抛物线
开口
对称轴
顶点
最值
增减性
y=ax2+bx+c(a>0)
y=ax2+bx+c(a<0)
向上
向下
在对称轴的左侧,y随着x的增大而减小。 在对称轴的右侧, y随着x的增大而增大。
在对称轴的左侧,y随着x的增大而增大。在对称轴的右侧, y随着x的增大而减小。
4、二次函数 y=ax2+bx+c 的图象和x轴交点的三种情况与一元二次方程根的关系:
二次函数y=ax2+bx+c的图象和x轴交点 一元二次方程ax2+bx+c= 0的根 一元二次方程ax2+bx+c= 0根的判别式Δ=b2-4ac
有两个交点
有两个不等的实数根
只有一个交点(顶点)
有两个相等的实数根
没有交点
没有实数根
b2 – 4ac > 0
b2 – 4ac = 0
b2 – 4ac < 0
(1)关键是求出待定系数____________的值。
(2)设解析式的三种形式:
①一般式:______________,当已知抛物线上三个点时,用一般式比较简便;
②顶点式:______________ ,当已知抛物线的顶点时,用顶点式较方便;
③交点式(两根式):__________________,当已知抛物线与 x 轴的交点坐标(x1,0),(x2,0)时,用交点式较方便。
a,b,c
y=ax2+bx+c
y=a(x-h)2+k
y=a(x-x1)(x-x2)
5、求二次函数 y=ax +bx+c 的解析式
例1 用配方法求出函数 y = -2x 2 - 4x + 6 的图象的对称轴、顶点坐标,画出函数图象,并说明图象是由抛物线y = -2x 2 经过怎样的平移得到的。
(-1,8)
(x + 1)+8
2
y = -2
对称轴是 x = -1。
是由抛物线 y = -2x 2 向左
平移 1 个单位,向上平移
8 个单位得到的。
y
8
6
4
2
-2
-4 -2 2 4 x
O
例题学习
例2
已知二次函数
(1)求抛物线开口方向,对称轴和顶点M的坐标;(2)设抛物线与y轴交于C点,与x轴交于A、B两点求C,A,B的坐标;
(3)x为何值时,y随x的增大而减少,x为何值时,y有最大(小)值,这个最大(小)值是多少?
(4)x为何值时,y<0?x为何值时,y>0?
例3 根据下列条件,求出二次函数的解析式。
图象经过(-1,1),(1,3),(0,1)三点;
(2)图象的顶点为(-1,-8),且过点(0,-6);
(x + 1)-8
2
y = 2
例4:某商场购进一批单价为16元的日用品,经实
验发现若按每件20元的价格销售时,每月能卖360
件,若按每件25元的价格销售时,每月能卖210件,假设每月销售件数为y(件)是价格x(元/件)的一次函数。
(1)试求y与x之间的函数关系式。
(2)在商品不积压,且不考虑其他因素的条件下,问:销售价格定为每件多少时,才能使每月获得最大利润?每月的最大利润是多少?
解:
(1)y=kx+b
把x=20时,y=360;x=25时,y=210分别代入上式
得 :
360=20k+b 210=25k+b
解得:
k=30,b=960
所以y与x之间的函数关系式为y=-30x+960(x≥16,且x为整数)
(2)设每月利润为P元,
P=y(x-16)=(30x+960)(x-16)
=-30x +1440x-15360
P为最大值:(-30×24+960)(24-16)=1920(元)
答:当销售价格为每件24元时,每月利润最大,最大利润为1920元。
应用训练
1.在二次函数y=ax2+bx+c中,ac >0,则它的图像与x轴的关系是( )
A. 没有交点 B. 有两个交点
C. 有一个交点 D. 不能确定
B
2.已知抛物线y=x2+px+q经过点(5,0),(-5,0),则 p+q=( )
A. 0 B. 25 C. -25 D. 5
C
3.若二次函数 y=ax2 +bx+c 的图象如下,与x轴的一个交点为(1,0),则下列各式中不成立的是( )
A. b2-4ac>0 B. abc>0
C. a+b+c=0 D. a-b+c<0
1
x
y
o
-1
B
4.方程x2-3x=0的两根是x1=0,x2=3,抛物线
与x轴交点坐标是 ( )
A. (0,0) (3,0) B. (0,0) (0,3)
C. (0,0) (-3,0) D. (0,0) (0,-3)
A
一、选择题
C
5.二次函数y=x2-x-2的图象如图所示,则函数值y<0时x的取值范围是( )
(A). x<-1 (B) x>2
(C). -1<x<2 (D) x<-1或x>2
x
y
o
-1
2
6.如图,两条抛物线y1= - x2+1,y2= - x2-1与分别经过点(-2,0),(2,0)且平行于y轴的两条平行线围成的阴影部分的面积为( )
(A)8 (B)6 (C)10 (D)4
2
1
2
1
A
7.如图,点A,B的坐标分别为(1, 4)和(4, 4),抛物线y=a(x-m)2+n的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为( )
(A)-3 (B)1 (C)5 (D)8
x
y
o
A(1,4)
B(4,4)
C
D
D
1.已知二次函数y=x2+mx+2的图像与x轴的一个交点是(2,0),则与x轴另一个交点_______,m=_________。
(1,0)
-3
二、填空题
2.当m______时,抛物线y=4x2-4x+m与x轴只有一个交点,交点是________。
=1
( ,0)
2
1
3. 若二次函数y=kx2+3x-5的图像与x轴有两个交点,则k的取值范围是__________________。
k>- 且k≠0
20
9
4.如果关于x的一元二次方程 x2-2x+m=0有两个相等的实数根,则m=_,此时抛物线 y=x2-2x+m与x轴有__个交点。
1
1
5.已知实数x,y满足x2+3x+y-3=0,则x+y的最大值为_____。
4
6.已知二次函数y=ax2+bx+c的图像如图,用不等式连结下列各式:a __0,b __0,c ___0,
b2-4ac___0 a+b+c___0,a-b+c___0。
>
>
>
>
<
<
1
-1
x
y
o
7.若二次函数y=-x2+2x+k的部分图象如图所示,关于x的一元二次方程-x2+2x+k=0的一个解x1=3,另一个解x2=_____。
-1
8.已知二次函数的图象的顶点坐标为(-2,-3),且图象过点(-3,-2),则此二次函数的解析式 ;设此二次函数的图象与x轴交于A,B两点,O为坐标原点,则线段OA,OB的长度之和是 。
9.某商场将进价40元一个的某种商品按50元一个售出时,能卖出500个,已知这种商品每个涨价1元,销量减少10个,设每个涨价x元,销售价可以表示为 ,一个商品所获利润可以表示为 ,销售量可以表示为 ________,利润可以为 ,因此,定价是 元时,最大利润是 元。
(50+x)元
(50+x-40)元
(500-10x) 个
(50+x-40)(500-10x)
70
9000
10.不论x为何值时,函数y=ax2+bx+c(a≠0)的值永远为正的条件是____ _ 。
a>0, b -4ac<0
y=x2+4x+1
2√3
1.已知二次函数y=ax2+bx+c的最大值是2,图象顶点在直线y=x+1上,并且图象经过点(3,-6)。求a、b、c。
三、解答题:
∵二次函数的最大值是2∴抛物线的顶点纵坐标为2
顶点在直线y=x+1上
当y=2时,x=1。∴顶点坐标为( 1 , 2)
设解析式为y=a(x-1)2+2
∴a=-2 y=-2(x-1)2+2 y=-2x2+4x
2.已知抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同,顶点在直线x=1上,且顶点到x轴的距离为5,请写出满足此条件的抛物线的解析式。
a=1或a=-1
又∵顶点在直线x=1上,且顶点到x轴的距离为5,
顶点为(1,5)或(1,-5)
所以其解析式为:
(1) y=(x-1)2+5 (2) y=(x-1)2-5
(3) y=-(x-1)2+5 (4) y=-(x-1)2-5
3.已知二次函数y= x2+x-
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,
A,B的坐标。
(3)画出函数图象的示意图。
(4)求ΔMAB的周长及面积。
(5)x为何值时,y随x的增大而减小,x为何值时,y有最大
(小)值,这个最大(小)值是多少?
(6)x为何值时,y<0?x为何值时,y>0?
2
1
2
3
对称轴x=-1,顶点坐标M(-1,-2)
与x轴交点A(-3,0)B(1,0)C(0, )
2
3
图略
ΔMAB的周长=2MA+AB=2√2 ×2+4=4√2+4
ΔMAB的面积= AB×MD= ×4×2=4
2
1
2
1
当x<-1时,y随x的增大而减小;
当x=-1时,y最小值=-2
当x< -3或x>1时,y > 0
当-3 < x < 1时,y < 0
4.已知二次函数y=(x-2a)2+(a-1)(a为常数),当a取不同的值时,
其图像构成一个“抛物线系”。下图分别是a=-1,a=0,a=1,
a=2时二次函数的图像。它们的顶点在一直线上,
求这条直线的解析式。
x
y
O
a=-1
a=2
a=1
a=0
由题意知,
二次函数的顶点坐标是(2a,a-1)
代入各个a的值,即可得直线解析式
或设x=2a,y=a-1,消去a,即得:y= x-1
2
1
5.已知抛物线y=x2-2x-8,
(1)求证:该抛物线与x轴一定有两个交点;
(2)若该抛物线与x轴的两个交点分别为A、B,且它的顶点为P,求△ABP的面积。
x
y
o
A
P
B
△=22-4×(-8)=36>0
x2-2x-8=0
解方程得:x1=4, x2=-2
∴AB=4-(-2)=6 而P点坐标是(1,-9)
∴S△ABC=27
6、抛物线 y=-2x2+4x+6 顶点为A,与x轴交于B、C两点,与y轴交于D点,求四边形ABCD的面积。
y=-2x2+4x+6=-2(x-1)2+8,图像如图
A(1,8) B(-1,0) C(3,0) D(0,6)
3
-1
x
y
o
D
C
B
A
E
S四边形ABCD=SΔBOD+S梯形OEAD+SΔAEC
18
7.丁丁推铅球的出手高度为1.6m,如图所示,铅球的运行
路线近似为抛物线y=-0.1(x-k)2+2.5
①求k的值
②求铅球的落点与丁丁的距离。
③一个1.5m的小朋友跑到离原点6米的地方(如图),他会受到伤害吗?
x
y
O
B
(0,1.6)
①当x=0时,y=1.6
k=±3
对称轴是在y轴的右侧,即x=k>0,k=3
②-0.1(x-3)2+2.5=0得,x1 =8,x2 =-2所以,OB=8,故铅球的落点与丁丁的距离是8米。
③当x=6时,y=-0.1(6-3)2+2.5=1.6
>1.5
所以,这个小朋友不会受到伤害。
9、已知二次函数y=ax2-5x+c的图象如图。
(1) 当x为何值时,y随x的增大而增大;
(2) 当x为何值时,y<0;
(3)求它的解析式和顶点坐标。
(1)求k的取值范围;
(2)设抛物线与x轴交于A、B两点,且点A在点B的左侧,
点D是抛物线的顶点。如果△ABD是等腰直角三角形,求抛物线的解析式;
(3)在(2)的条件下,抛物线与y轴交于点C, 点E在y轴的正半轴上且以A、O、E为顶点的三角形与△AOC相似。求点E坐标。
2
1
8、已知抛物线y= x2-x+k 与x轴有两个交点。
10.某企业投资100万元引进一条产品加工生产线,若不计维修、保养费用,预计投产后每年可创利33万。该生产线投产后,从第1年到第x年的维修、保养费用累计为y(万元),且y=ax2+bx,若第1年的维修、保养 、费用为2万元,到第2年为6万元。
(1)求y的解析式;
(2)投产后,这个企业在第几年就能收回投资?
解:(1)由题意,x=1时,y=2;x=2时,y=2+4=6。分别代入y=ax2+bx,得a+b=2,4a+2b=6,
解得:a=1,b=1, ∴y=x2+x。
(2)设f=33x-100-x2-x,则
f=-x2+32x-100=-(x-16)2+156。
由于当1≤x≤16时,f随x的增大而增大,故当x=4时,即第4年可收回投资。
11.李明投资销售一种进价为每件20元的护眼台灯。销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=-10x+500。
(1)设李明每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(2)如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?(成本=进价×销售量)
(1)由题意,得:w=(x-20)·y=(x-20)·(-10x+500) =-10x2+700x-10 000
答:当销售单价定为35元时,每月可获得最大利润。
(2)由题意,得:-10x2+700x-10 000=2 000
解这个方程得:x1=30,x2=40。
答:李明想要每月获得2 000元的利润,销售单价应定为30元或40元。
(3)方法一:∵a=-10<0,∴抛物线开口向下。
∴当30≤x≤40时,w≥2 000。∵x≤32,∴当30≤x≤32时w≥2000。
设成本为P(元),由题意,得:
P=20×(-10x+500)=-200x+10 000
∵k=-200<0,∴P随x的增大而减小。
∴当x=32时,P最小=3600。
答:每月获得利润不低于2000元,每月成本最少为3600元。
方法二:∵a=-10<0,∴抛物线开口向下。
∴当30≤x≤40时,w≥2000。∵x≤32,∴30≤x≤32时,w≥2000。∵y=-10x+500,k=-10<0,∴y随x的增大而减小。∴当x=32时,y最小=180,
∵当进价一定时,销售量越小,成本越小,
∴20×180=3 600(元)
答:想要每月获得利润不低于2000元,每月成本最少为3600元。
12.用长为12 m的篱笆,一边利用足够长的墙围出一块苗圃。如图,围出的苗圃是五边形ABCDE,AE⊥AB,BC⊥AB,∠C=∠D=∠E。设CD=DE=x m,五边形ABCDE的面积为S m2问当x取什么值时,S最大?并求出S的最大值。
连结EC,作DF⊥EC,垂足为F。
∵∠DCB=∠CDE=∠DEA,
∠EAB=∠CBA=90°,
∴∠DCB=∠CDE=∠DEA=120°。
∵DE=CD,∴∠DEC=∠DCE=30°,
∴∠CEA=∠ECB=90°,
∴四边形EABC为矩形,又∵DE=x,
∴AE=6-x,DF= x,EC=√3x,
2
1
S= - x2+6√3x (0
4
当x=4m时,S最大=12√3m2
谢 谢
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
