苏科版九年级下册 5.5 用二次函数解决问题 课件(共17张PPT)
文档属性
| 名称 | 苏科版九年级下册 5.5 用二次函数解决问题 课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 251.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-29 22:04:35 | ||
图片预览





文档简介
(共17张PPT)
5.5 用二次函数解决问题
学习目标:
1.通过存在性问题的探讨,能快速、正确地求出二次函数的解析式,并能运用二次函数的性质和相关知识解决问题;
2. 通过存在性问题的探讨,进一步提升综合运用知识进行分析问题、解决问题的能力.
学习重点:
与相似有关的存在性问题、与面积有关的存在性问题.
学习难点:
问题的分析、解决能力和综合运用知识能力的提升.
存在性问题
存在性问题
内容解读
存在性问题是指判断满足某种条件的事物是否存在的问题.这类问题知识覆盖面广,综合性强,题意构思精巧,解题方法灵活,对同学们分析问题和解决问题的能力要求较高,是近几年来各地中考的“热点”.
存在性问题的一般思路:先对结论作出肯定的假设,然后由肯定假设出发,结合已知条件或挖掘出隐含条件,辅以方程思想等,进行正确的计算、推理,再对得出的结果进行检验,判断是否与题设、公理、定理等吻合.若无矛盾,则说明假设正确,由此得出符合条件的数学对象存在;否则,说明不存在.
存在性问题
Ⅰ.与相似有关的存在性问题
问题1.如图,抛物线y= x2+bx+c经过△ABC的三个顶点,其中点A(0,1)、点B(-9,10),AC//x轴,P是直线AC下方抛物线上的动点.
例1图
问题探究
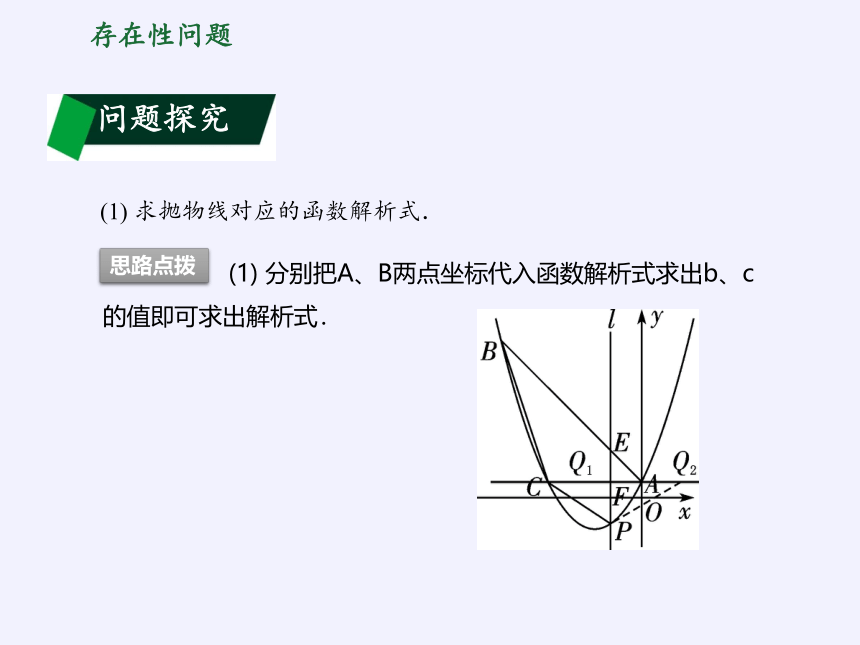
(1) 求抛物线对应的函数解析式.
(1) 分别把A、B两点坐标代入函数解析式求出b、c的值即可求出解析式.
思路点拨
存在性问题
问题探究
存在性问题
(2) 过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标.
(2) 由于点P在抛物线上,故可设出点P的坐标,然后求出直线AB对应的函数解析式,从而可以表示出点E的坐标,则S四边形AECP=S△AEC+S△APC= AC EP,转化为二次函数求最值,即可求出四边形面积的最大值以及点P的坐标.
思路点拨
问题探究
存在性问题
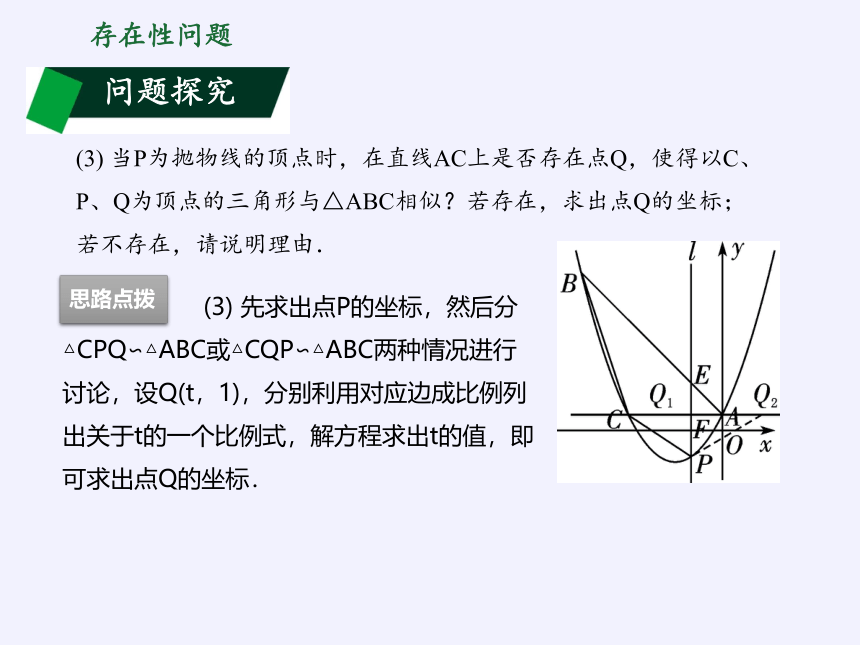
(3) 当P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由.
(3) 先求出点P的坐标,然后分△CPQ∽△ABC或△CQP∽△ABC两种情况进行讨论,设Q(t,1),分别利用对应边成比例列出关于t的一个比例式,解方程求出t的值,即可求出点Q的坐标.
思路点拨
问题探究
存在性问题
方法归纳
(1) 求二次函数的解析式有三种形式:交点式、一般式、顶点式,用待定系数法来求二次函数的解析式时,要注意根据题意选择合理形式来简化计算.(2) 求四边形的面积最大值,关键是利用数形结合思想,将四边形分割成两个三角形,然后利用这两个三角形面积的和解决,而求此四边形面积的最值,一般要转化为顶点式来求.(3) 要使题目所求的两个三角形相似,需进行分类讨论,避免出现漏解的情况.
问题2.已知抛物线y=ax2-4a(a>0)与x轴相交于A、B两点(点A在点B的左侧),点P是抛物线上一点,且PB=AB,∠PBA=120°,如图①所示.
例2图
存在性问题
问题探究
Ⅱ.与面积有关的存在性问题
存在性问题
问题探究
(1) 求抛物线对应的函数解析式.
(1) 先求出A、B两点的坐标,然后过点P作PC⊥x轴于点C,根据∠PBA=120°,PB=AB,分别求出BC和PC的长度,即可得出点P的坐标,最后将点P的坐标代入二次函数解析式即可.
思路点拨
存在性问题
问题探究
(2) 设点M(m,n)为抛物线上的一个动点,且在曲线PA上移动.
① 如图②,当点M在曲线PB之间(含端点)移动时,是否存在点M使△APM的面积为 ?若存在,求出点M的坐标;若不存在,请说明理由.
(2) ① 过点M作ME⊥x轴于点E,交AP于点D,分别用含m的式子表示点D、E的坐标,然后代入△APM的面积公式 DM AE + DM CE= DM AC,根据题意列出方程求出m的值;
思路点拨
存在性问题
问题探究
② 如图③,当点M在曲线BA之间(含端点)移动时,求|m|+|n|的最大值及取得最大值时点M的坐标.
② 根据题意可知n<0,然后对m的值进行分类讨论,当-2≤m≤0时,|m|=-m;当0思路点拨
存在性问题
方法归纳
本题涉及用待定系数法求二次函数解析式、三角形面积公式、二次函数最值等知识,要注意将三角形面积分解成两个三角形面积求和;对于用坐标表示三角形的面积,还需要注意绝对值的化简计算,求最大值时借助于二次函数的性质解决问题.
存在性问题
问题再思考
1.结合课堂中的两个问题思考,当我们遇到二次函数存在性问题时,解题的一般思路怎样?应注意什么问题?
2.完成课堂问题的解题过程.
存在性问题
作 业
《练案》P102 存在性问题.
存在性问题
课后自主探究
与特殊图形的判定有关的存在性问题
如图,抛物线经过A(-1,0)、B(5,0)、C(0,- )三点.
(1) 求抛物线对应的函数解析式.
(3) 分点N在x轴下方或上方两种情况进行讨论.
(2) 在抛物线的对称轴上有一点P,使PA+PC的值最小,求出点P的坐标.
谢 谢
5.5 用二次函数解决问题
学习目标:
1.通过存在性问题的探讨,能快速、正确地求出二次函数的解析式,并能运用二次函数的性质和相关知识解决问题;
2. 通过存在性问题的探讨,进一步提升综合运用知识进行分析问题、解决问题的能力.
学习重点:
与相似有关的存在性问题、与面积有关的存在性问题.
学习难点:
问题的分析、解决能力和综合运用知识能力的提升.
存在性问题
存在性问题
内容解读
存在性问题是指判断满足某种条件的事物是否存在的问题.这类问题知识覆盖面广,综合性强,题意构思精巧,解题方法灵活,对同学们分析问题和解决问题的能力要求较高,是近几年来各地中考的“热点”.
存在性问题的一般思路:先对结论作出肯定的假设,然后由肯定假设出发,结合已知条件或挖掘出隐含条件,辅以方程思想等,进行正确的计算、推理,再对得出的结果进行检验,判断是否与题设、公理、定理等吻合.若无矛盾,则说明假设正确,由此得出符合条件的数学对象存在;否则,说明不存在.
存在性问题
Ⅰ.与相似有关的存在性问题
问题1.如图,抛物线y= x2+bx+c经过△ABC的三个顶点,其中点A(0,1)、点B(-9,10),AC//x轴,P是直线AC下方抛物线上的动点.
例1图
问题探究
(1) 求抛物线对应的函数解析式.
(1) 分别把A、B两点坐标代入函数解析式求出b、c的值即可求出解析式.
思路点拨
存在性问题
问题探究
存在性问题
(2) 过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标.
(2) 由于点P在抛物线上,故可设出点P的坐标,然后求出直线AB对应的函数解析式,从而可以表示出点E的坐标,则S四边形AECP=S△AEC+S△APC= AC EP,转化为二次函数求最值,即可求出四边形面积的最大值以及点P的坐标.
思路点拨
问题探究
存在性问题
(3) 当P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由.
(3) 先求出点P的坐标,然后分△CPQ∽△ABC或△CQP∽△ABC两种情况进行讨论,设Q(t,1),分别利用对应边成比例列出关于t的一个比例式,解方程求出t的值,即可求出点Q的坐标.
思路点拨
问题探究
存在性问题
方法归纳
(1) 求二次函数的解析式有三种形式:交点式、一般式、顶点式,用待定系数法来求二次函数的解析式时,要注意根据题意选择合理形式来简化计算.(2) 求四边形的面积最大值,关键是利用数形结合思想,将四边形分割成两个三角形,然后利用这两个三角形面积的和解决,而求此四边形面积的最值,一般要转化为顶点式来求.(3) 要使题目所求的两个三角形相似,需进行分类讨论,避免出现漏解的情况.
问题2.已知抛物线y=ax2-4a(a>0)与x轴相交于A、B两点(点A在点B的左侧),点P是抛物线上一点,且PB=AB,∠PBA=120°,如图①所示.
例2图
存在性问题
问题探究
Ⅱ.与面积有关的存在性问题
存在性问题
问题探究
(1) 求抛物线对应的函数解析式.
(1) 先求出A、B两点的坐标,然后过点P作PC⊥x轴于点C,根据∠PBA=120°,PB=AB,分别求出BC和PC的长度,即可得出点P的坐标,最后将点P的坐标代入二次函数解析式即可.
思路点拨
存在性问题
问题探究
(2) 设点M(m,n)为抛物线上的一个动点,且在曲线PA上移动.
① 如图②,当点M在曲线PB之间(含端点)移动时,是否存在点M使△APM的面积为 ?若存在,求出点M的坐标;若不存在,请说明理由.
(2) ① 过点M作ME⊥x轴于点E,交AP于点D,分别用含m的式子表示点D、E的坐标,然后代入△APM的面积公式 DM AE + DM CE= DM AC,根据题意列出方程求出m的值;
思路点拨
存在性问题
问题探究
② 如图③,当点M在曲线BA之间(含端点)移动时,求|m|+|n|的最大值及取得最大值时点M的坐标.
② 根据题意可知n<0,然后对m的值进行分类讨论,当-2≤m≤0时,|m|=-m;当0
存在性问题
方法归纳
本题涉及用待定系数法求二次函数解析式、三角形面积公式、二次函数最值等知识,要注意将三角形面积分解成两个三角形面积求和;对于用坐标表示三角形的面积,还需要注意绝对值的化简计算,求最大值时借助于二次函数的性质解决问题.
存在性问题
问题再思考
1.结合课堂中的两个问题思考,当我们遇到二次函数存在性问题时,解题的一般思路怎样?应注意什么问题?
2.完成课堂问题的解题过程.
存在性问题
作 业
《练案》P102 存在性问题.
存在性问题
课后自主探究
与特殊图形的判定有关的存在性问题
如图,抛物线经过A(-1,0)、B(5,0)、C(0,- )三点.
(1) 求抛物线对应的函数解析式.
(3) 分点N在x轴下方或上方两种情况进行讨论.
(2) 在抛物线的对称轴上有一点P,使PA+PC的值最小,求出点P的坐标.
谢 谢
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
