苏科版九年级下册 5.5 用二次函数解决问题 学案(无答案)
文档属性
| 名称 | 苏科版九年级下册 5.5 用二次函数解决问题 学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 406.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-29 22:06:56 | ||
图片预览

文档简介
用二次函数解决问题
【学习目标】
用三角形相似,对应线段成比例,面积公式等,分析和表示不同背景下实际问题中的变量之间的二次函数关系,并运用二次函数的知识解决实际问题。
【学习重难点】
运用二次函数的知识解决实际问题。
【学习过程】
一、问题导学
如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上。
(1)设矩形的一边AB=x cm,那么AD边的长度如何表示?
(2)设矩形的面积为ym ,当x取何值时,y的最大值是多少?
二、生生互动
1.某建筑物窗户如图所示,它的上半部是半圆,下半部是矩形。制造窗框的材料总长(图中所有黑线的长度和)为15m。当x等于多少时,窗户透过的光线最多(结果精确到0.01m)?此时,窗户的面积是多少?
三、师生互动:
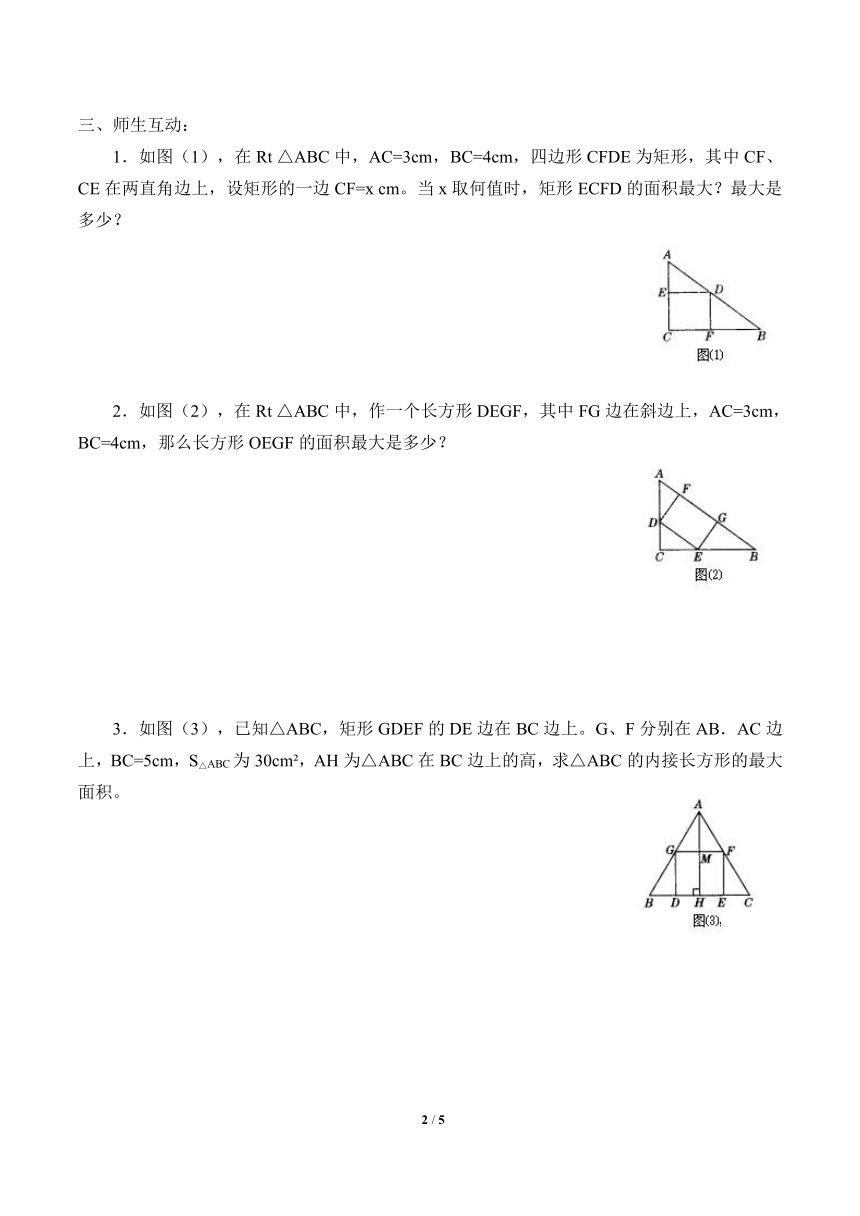
1.如图(1),在Rt △ABC中,AC=3cm,BC=4cm,四边形CFDE为矩形,其中CF、CE在两直角边上,设矩形的一边CF=x cm。当x取何值时,矩形ECFD的面积最大?最大是多少?
2.如图(2),在Rt △ABC中,作一个长方形DEGF,其中FG边在斜边上,AC=3cm,BC=4cm,那么长方形OEGF的面积最大是多少?
3.如图(3),已知△ABC,矩形GDEF的DE边在BC边上。G、F分别在AB.AC边上,BC=5cm,S△ABC为30cm ,AH为△ABC在BC边上的高,求△ABC的内接长方形的最大面积。
【达标检测】
1.二次函数y=x -3x-4的顶点坐标是 , 对称轴是直线 ,与x轴的交点是 ,当x= 时,y有最 ,是 。
2.二次函数y=ax +bx+c的图像如图所示,则a 0,b 0,c 0.
当x 时, y<0,
3.周长为16cm的矩形的最大面积为 ,实际上此时矩形是 。
4.已知二次函数y=x -6x+m的最小值为1,则m的值是 。
5.如果一条抛物线与抛物线y=-x +2的形状、开口方向相同,且顶点坐标是(4,-2),则它的表达式是 。
6.若抛物线y=3x +mx+3的顶点在x轴的负半轴上,则m的值为 。
7.抛物线y=3x -2向左平移2个单位,向下平移3个单位,则所得抛物线为( )
A.y=3(x+2)2+1 B.y=3(x-2)2-1
C.y=3(x+2)2-5 D.y=3(x-2)2-2
8.二次函数y=x +mx+n,若m+n=0,则它的图像必经过点( )
A.(-1,1) B.(1,-1) C.(-1,-1) D.(1,1)
9.如图3,有一块铁皮,拱形边缘呈抛物线状,MN=4dm,抛物线顶点到MN的距离是4dm。要在铁皮上截下一矩形ABCD,使矩形顶点B、C落在MN上,A.D落在抛物线上,试问这样截下的矩形铁皮周长能否等于8dm?
10.在一直角三角形中建造一个内接于△ABC的矩形水池DEFN。其中DE在AB上,AC=8,BC=6.
(1)求△ABC中AB边上的高h;
(2)设DN=x,当x取何值时,水池DEFN的面积最大?
(3)实际施工时,发现在AB上距B点1.85处有一棵大树,问这棵大树是否位于最大矩形水池的边上?
11.某公司生产的A种产品,它的成本是2元,售价是3元,年销售量为10万件。为了获得更好的效益,公司准备拿出一定的资金做广告。根据经验,每年投入的广告费是x(10万元)时,产品的年销售量将是原销售量的y倍,且y是x的二次函数,它们的关系如下表:
x(10万元) 0 1 2 …
y 1 1.5 1.8 …
(1)求y与x的函数表达式;
(2)如果把利润看作是销售总额减去成本和广告费,试写出年利润S(10万元)与广告费x(10万元)函数表达式;
(3)如果投入的广告费为10万元~30万元,问广告费在什么范围内,公司获得的年利润随广告费的增大而增大?
12.有一块形状是直角梯形的铁皮ABCD,它的上底AD=3cm,下底BC=8cm,垂直于底的腰CD=6cm。现要裁成一块矩形铁皮MPCN,使它的顶点M、P、N分别在AB.BC.CD上。当MN是多长时,矩形MPCN的面积有最大值?
5 / 5
【学习目标】
用三角形相似,对应线段成比例,面积公式等,分析和表示不同背景下实际问题中的变量之间的二次函数关系,并运用二次函数的知识解决实际问题。
【学习重难点】
运用二次函数的知识解决实际问题。
【学习过程】
一、问题导学
如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上。
(1)设矩形的一边AB=x cm,那么AD边的长度如何表示?
(2)设矩形的面积为ym ,当x取何值时,y的最大值是多少?
二、生生互动
1.某建筑物窗户如图所示,它的上半部是半圆,下半部是矩形。制造窗框的材料总长(图中所有黑线的长度和)为15m。当x等于多少时,窗户透过的光线最多(结果精确到0.01m)?此时,窗户的面积是多少?
三、师生互动:
1.如图(1),在Rt △ABC中,AC=3cm,BC=4cm,四边形CFDE为矩形,其中CF、CE在两直角边上,设矩形的一边CF=x cm。当x取何值时,矩形ECFD的面积最大?最大是多少?
2.如图(2),在Rt △ABC中,作一个长方形DEGF,其中FG边在斜边上,AC=3cm,BC=4cm,那么长方形OEGF的面积最大是多少?
3.如图(3),已知△ABC,矩形GDEF的DE边在BC边上。G、F分别在AB.AC边上,BC=5cm,S△ABC为30cm ,AH为△ABC在BC边上的高,求△ABC的内接长方形的最大面积。
【达标检测】
1.二次函数y=x -3x-4的顶点坐标是 , 对称轴是直线 ,与x轴的交点是 ,当x= 时,y有最 ,是 。
2.二次函数y=ax +bx+c的图像如图所示,则a 0,b 0,c 0.
当x 时, y<0,
3.周长为16cm的矩形的最大面积为 ,实际上此时矩形是 。
4.已知二次函数y=x -6x+m的最小值为1,则m的值是 。
5.如果一条抛物线与抛物线y=-x +2的形状、开口方向相同,且顶点坐标是(4,-2),则它的表达式是 。
6.若抛物线y=3x +mx+3的顶点在x轴的负半轴上,则m的值为 。
7.抛物线y=3x -2向左平移2个单位,向下平移3个单位,则所得抛物线为( )
A.y=3(x+2)2+1 B.y=3(x-2)2-1
C.y=3(x+2)2-5 D.y=3(x-2)2-2
8.二次函数y=x +mx+n,若m+n=0,则它的图像必经过点( )
A.(-1,1) B.(1,-1) C.(-1,-1) D.(1,1)
9.如图3,有一块铁皮,拱形边缘呈抛物线状,MN=4dm,抛物线顶点到MN的距离是4dm。要在铁皮上截下一矩形ABCD,使矩形顶点B、C落在MN上,A.D落在抛物线上,试问这样截下的矩形铁皮周长能否等于8dm?
10.在一直角三角形中建造一个内接于△ABC的矩形水池DEFN。其中DE在AB上,AC=8,BC=6.
(1)求△ABC中AB边上的高h;
(2)设DN=x,当x取何值时,水池DEFN的面积最大?
(3)实际施工时,发现在AB上距B点1.85处有一棵大树,问这棵大树是否位于最大矩形水池的边上?
11.某公司生产的A种产品,它的成本是2元,售价是3元,年销售量为10万件。为了获得更好的效益,公司准备拿出一定的资金做广告。根据经验,每年投入的广告费是x(10万元)时,产品的年销售量将是原销售量的y倍,且y是x的二次函数,它们的关系如下表:
x(10万元) 0 1 2 …
y 1 1.5 1.8 …
(1)求y与x的函数表达式;
(2)如果把利润看作是销售总额减去成本和广告费,试写出年利润S(10万元)与广告费x(10万元)函数表达式;
(3)如果投入的广告费为10万元~30万元,问广告费在什么范围内,公司获得的年利润随广告费的增大而增大?
12.有一块形状是直角梯形的铁皮ABCD,它的上底AD=3cm,下底BC=8cm,垂直于底的腰CD=6cm。现要裁成一块矩形铁皮MPCN,使它的顶点M、P、N分别在AB.BC.CD上。当MN是多长时,矩形MPCN的面积有最大值?
5 / 5
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
