立体图形的表面积和体积课件(共22张PPT)六年级下册数学苏教版
文档属性
| 名称 | 立体图形的表面积和体积课件(共22张PPT)六年级下册数学苏教版 |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-29 17:28:47 | ||
图片预览






文档简介
(共22张PPT)
立体图形的表面积和体积
整理与复习
知识梳理
小组活动要求:
1.说一说:自己的收获。
2.记一记:用红笔进行补充。
3.想一想:在有疑问的地方做上记号。
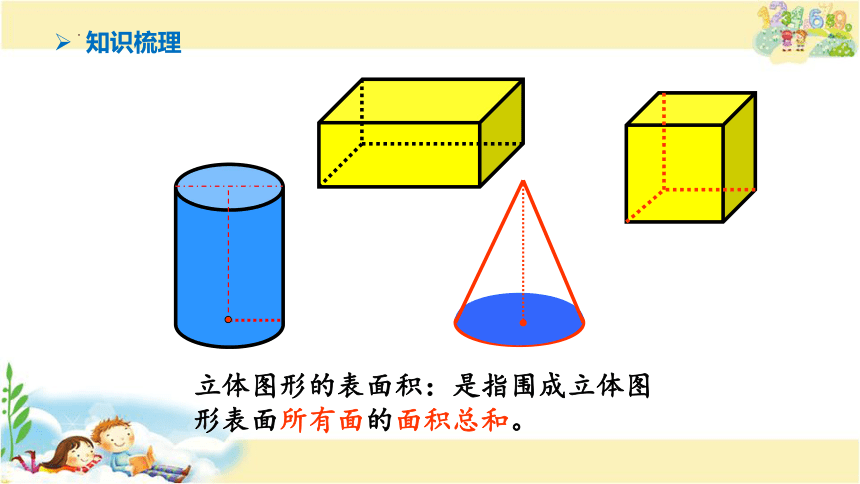
立体图形的表面积:是指围成立体图 形表面所有面的面积总和。
知识梳理
小组讨论一:
1、说一说,长方体、正方体、圆柱体的表面积如何计算?
2、写一写,长方体、正方体、圆柱体表面积的计算公式用字母怎样表示?
3、想一想,圆柱的侧面沿高剪开是什么形状的?展开后长方形的长、宽与圆柱有什么关系?还可以怎样剪?圆柱侧面积怎样计算?
知识梳理
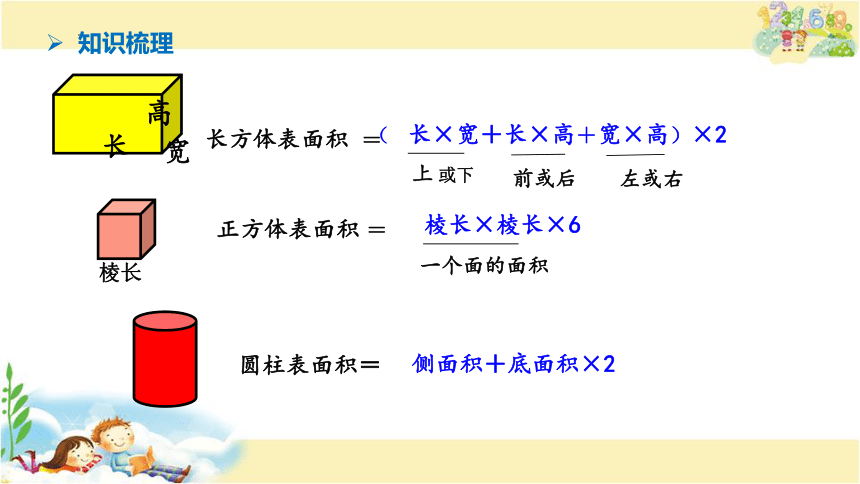
长方体表面积 =
( 长×宽+长×高+宽×高)×2
正方体表面积 =
棱长×棱长×6
圆柱表面积=
侧面积+底面积×2
上 或下
前或后
左或右
一个面的面积
长
宽
高
棱长
知识梳理
3、圆柱的侧面沿高剪开是什么形状的?展开后长方形的长、宽与圆柱有什么关系?还可以怎样剪?圆柱侧面积怎样计算?
长=圆柱的底面周长
宽=圆柱的高
圆柱侧面积=底面周长×高
底=圆柱的底面周长
高= 圆柱的高
知识梳理
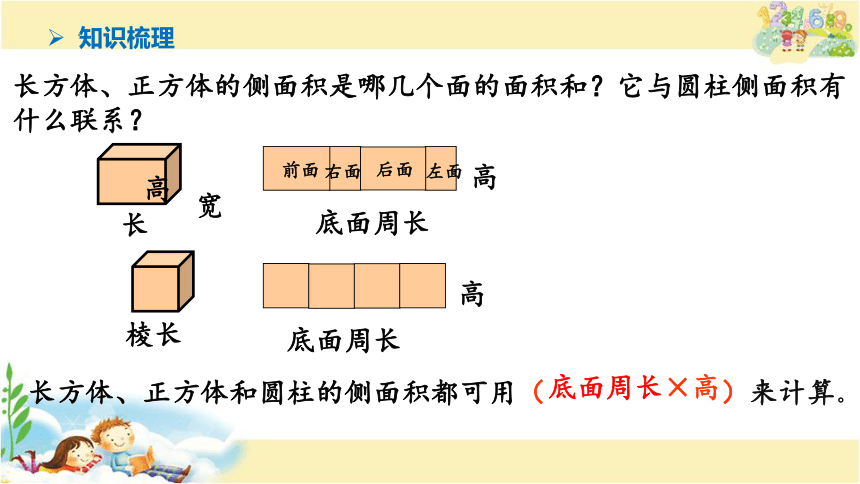
长方体、正方体的侧面积是哪几个面的面积和?它与圆柱侧面积有什么联系?
长方体、正方体和圆柱的侧面积都可用( )来计算。
长
宽
高
高
棱长
底面周长
高
前面
右面
左面
后面
底面周长
底面周长×高
知识梳理
练习与实践
1.圆柱形队鼓的侧面由铝皮围成,上下底面蒙的是羊皮。做一个这样的队鼓。
(1)至少需要铝皮多少平方分米?( )
A. π× 6÷2×2.6 B. π×6×2.6 C. 6×2.6
(2)至少需要羊皮多少平方分米?( )
A. π×62×2 B. π ×(6÷2)2 C. π× (6÷2) 2×2
6dm
2.6dm
B
C
练习与实践
6分米
2.6分米
2. 制作下面的圆柱形物体,至少各需要多少铁皮?
油桶
水桶
通风管
底面半径4dm
高12dm
底面直径40cm
高50cm
管口周长0.628m
长1.2m
侧面积:π×4×2×12=96π(平方分米)
底面积:π×42=16π (平方分米)
表面积:16π×2+96π =128π(平方分米)
答:制作这个油桶至少需要128π平方分米铁皮。
练习与实践
底面半径 4 分米
高12分米
底面直径40厘米
高50厘米
管口周长0.628米,长1.2米
侧面积:π×40×50=2000π(平方厘米)
底面积:π×(40÷2)2=400π (平方厘米)
400π+2000π =2400π(平方厘米)
答:制作这个水桶至少需要2400π平方厘米铁皮。
0.628×1.2=0.7536平方米
1.什么是物体的体积?什么是容器的容积?
2.体积和容积有什么联系和区别?
3.常用的体积和容积单位有哪些?(用手比划一下大小)相邻的单位进率是多少?
小组活动二:
知识梳理
物体的体积:物体所占空间的大小。
物体的容积:容器能够容纳物体的体积。
立方米(m3)
立方分米(dm3)
立方厘米(cm3)
升(L)
毫升(ml)
1000
1000
1000
知识梳理
3. 在括号里填合适的单位。
(1)一间卧室地面的面积是 15( )。
平方米
(2)一瓶牛奶大约有 250( )。
(3)一间教室的空间大约是 144( )。
(4)一台微波炉的体积是 92( ),容积是25( )
毫升
立方米
立方分米
升
练习与实践
1. 长方体、正方体、圆柱和圆锥的体积各怎样计算?
2.这些公式分别是怎样推导出来的?
3.根据这几个体积公式的推导过程,思考:它们之间有什么样的联系?
小组活动三:
知识梳理
6厘米
3厘米
2厘米
知识梳理
把圆柱的底面平均分成16份,切开后照下图的样子拼一拼。
圆柱
长方体
知识梳理
知识梳理
我们学过的体积公式是怎样推导出来的?
V=ɑbh
V=
V=Sh
体积=底面积×高
V=
知识梳理
6.王冬家新买了一台柜式空调,它的外包装是一个长0.6米、宽0.4米、高1.8米的长方体纸箱。 做这样一个纸箱至少需要硬纸板多少平方米?(接头处忽略不计)
(0.6×1.8+0.4×1.8+0.6×0.4)×2
=(1.08+0.72+0.24)×2
= 2.04×2
=4.08(平方米)
答:做这样一个纸箱至少需要硬纸板4.08平方米。
练习与实践
提示:长方体纸箱有6个面
(1) 它左侧门的玻璃打碎了,要重新配一块。重新配上的玻璃是多少平方分米?
(2)如果把这个鱼缸放在桌子上,桌面被它盖住的面积有多大?
(3)把一个底面直径是4分米,高4分米的圆柱形小桶里装满水倒入鱼缸中(它们的厚度忽略不计),能倒满吗?
(4)如果鱼缸装满水后,把一个底面周长是80厘米的正方体浸没进去,水会溢出多少立方厘米?
一个长方体鱼缸,长40厘米,宽40厘米,高35厘米。
拓展与应用
一个用塑料薄膜覆盖的蔬菜大棚,长10米,横截面是一个半径2米的半圆。
(1)这个大棚的种植面积最大是多少?
(2)搭建这个大棚至少要用塑料薄膜多少平方米?(含两端的面积)
(3)搭建的这个大棚里空间有多少立方米?
拓展与应用
通过今天的整理,你又有了哪些收获?做题有什么好的建议分享给同学?
回顾与反思
立体图形的表面积和体积
整理与复习
知识梳理
小组活动要求:
1.说一说:自己的收获。
2.记一记:用红笔进行补充。
3.想一想:在有疑问的地方做上记号。
立体图形的表面积:是指围成立体图 形表面所有面的面积总和。
知识梳理
小组讨论一:
1、说一说,长方体、正方体、圆柱体的表面积如何计算?
2、写一写,长方体、正方体、圆柱体表面积的计算公式用字母怎样表示?
3、想一想,圆柱的侧面沿高剪开是什么形状的?展开后长方形的长、宽与圆柱有什么关系?还可以怎样剪?圆柱侧面积怎样计算?
知识梳理
长方体表面积 =
( 长×宽+长×高+宽×高)×2
正方体表面积 =
棱长×棱长×6
圆柱表面积=
侧面积+底面积×2
上 或下
前或后
左或右
一个面的面积
长
宽
高
棱长
知识梳理
3、圆柱的侧面沿高剪开是什么形状的?展开后长方形的长、宽与圆柱有什么关系?还可以怎样剪?圆柱侧面积怎样计算?
长=圆柱的底面周长
宽=圆柱的高
圆柱侧面积=底面周长×高
底=圆柱的底面周长
高= 圆柱的高
知识梳理
长方体、正方体的侧面积是哪几个面的面积和?它与圆柱侧面积有什么联系?
长方体、正方体和圆柱的侧面积都可用( )来计算。
长
宽
高
高
棱长
底面周长
高
前面
右面
左面
后面
底面周长
底面周长×高
知识梳理
练习与实践
1.圆柱形队鼓的侧面由铝皮围成,上下底面蒙的是羊皮。做一个这样的队鼓。
(1)至少需要铝皮多少平方分米?( )
A. π× 6÷2×2.6 B. π×6×2.6 C. 6×2.6
(2)至少需要羊皮多少平方分米?( )
A. π×62×2 B. π ×(6÷2)2 C. π× (6÷2) 2×2
6dm
2.6dm
B
C
练习与实践
6分米
2.6分米
2. 制作下面的圆柱形物体,至少各需要多少铁皮?
油桶
水桶
通风管
底面半径4dm
高12dm
底面直径40cm
高50cm
管口周长0.628m
长1.2m
侧面积:π×4×2×12=96π(平方分米)
底面积:π×42=16π (平方分米)
表面积:16π×2+96π =128π(平方分米)
答:制作这个油桶至少需要128π平方分米铁皮。
练习与实践
底面半径 4 分米
高12分米
底面直径40厘米
高50厘米
管口周长0.628米,长1.2米
侧面积:π×40×50=2000π(平方厘米)
底面积:π×(40÷2)2=400π (平方厘米)
400π+2000π =2400π(平方厘米)
答:制作这个水桶至少需要2400π平方厘米铁皮。
0.628×1.2=0.7536平方米
1.什么是物体的体积?什么是容器的容积?
2.体积和容积有什么联系和区别?
3.常用的体积和容积单位有哪些?(用手比划一下大小)相邻的单位进率是多少?
小组活动二:
知识梳理
物体的体积:物体所占空间的大小。
物体的容积:容器能够容纳物体的体积。
立方米(m3)
立方分米(dm3)
立方厘米(cm3)
升(L)
毫升(ml)
1000
1000
1000
知识梳理
3. 在括号里填合适的单位。
(1)一间卧室地面的面积是 15( )。
平方米
(2)一瓶牛奶大约有 250( )。
(3)一间教室的空间大约是 144( )。
(4)一台微波炉的体积是 92( ),容积是25( )
毫升
立方米
立方分米
升
练习与实践
1. 长方体、正方体、圆柱和圆锥的体积各怎样计算?
2.这些公式分别是怎样推导出来的?
3.根据这几个体积公式的推导过程,思考:它们之间有什么样的联系?
小组活动三:
知识梳理
6厘米
3厘米
2厘米
知识梳理
把圆柱的底面平均分成16份,切开后照下图的样子拼一拼。
圆柱
长方体
知识梳理
知识梳理
我们学过的体积公式是怎样推导出来的?
V=ɑbh
V=
V=Sh
体积=底面积×高
V=
知识梳理
6.王冬家新买了一台柜式空调,它的外包装是一个长0.6米、宽0.4米、高1.8米的长方体纸箱。 做这样一个纸箱至少需要硬纸板多少平方米?(接头处忽略不计)
(0.6×1.8+0.4×1.8+0.6×0.4)×2
=(1.08+0.72+0.24)×2
= 2.04×2
=4.08(平方米)
答:做这样一个纸箱至少需要硬纸板4.08平方米。
练习与实践
提示:长方体纸箱有6个面
(1) 它左侧门的玻璃打碎了,要重新配一块。重新配上的玻璃是多少平方分米?
(2)如果把这个鱼缸放在桌子上,桌面被它盖住的面积有多大?
(3)把一个底面直径是4分米,高4分米的圆柱形小桶里装满水倒入鱼缸中(它们的厚度忽略不计),能倒满吗?
(4)如果鱼缸装满水后,把一个底面周长是80厘米的正方体浸没进去,水会溢出多少立方厘米?
一个长方体鱼缸,长40厘米,宽40厘米,高35厘米。
拓展与应用
一个用塑料薄膜覆盖的蔬菜大棚,长10米,横截面是一个半径2米的半圆。
(1)这个大棚的种植面积最大是多少?
(2)搭建这个大棚至少要用塑料薄膜多少平方米?(含两端的面积)
(3)搭建的这个大棚里空间有多少立方米?
拓展与应用
通过今天的整理,你又有了哪些收获?做题有什么好的建议分享给同学?
回顾与反思
