圆锥的体积课件(共18张PPT)六年级下册数学苏教版
文档属性
| 名称 | 圆锥的体积课件(共18张PPT)六年级下册数学苏教版 |  | |
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-29 18:04:41 | ||
图片预览




文档简介
(共18张PPT)
圆锥的体积
数学小讲师
一个圆柱形水杯,底面半径是0.4分米,高是1.5分米。这个圆柱形水杯的体积是多少立方分米?
0.42×π×1.5=0.24π(立方分米)
答:个圆柱形水杯的体积是0.24π立方分米。
知识梳理
小组交流:
1.说一说圆锥的特征?
2.猜测:等底等高的圆锥的体积是圆柱体积的几分之几?
3.用什么办法验证你的猜测?
4.圆锥的体积公式是什么?
圆锥有什么特征?
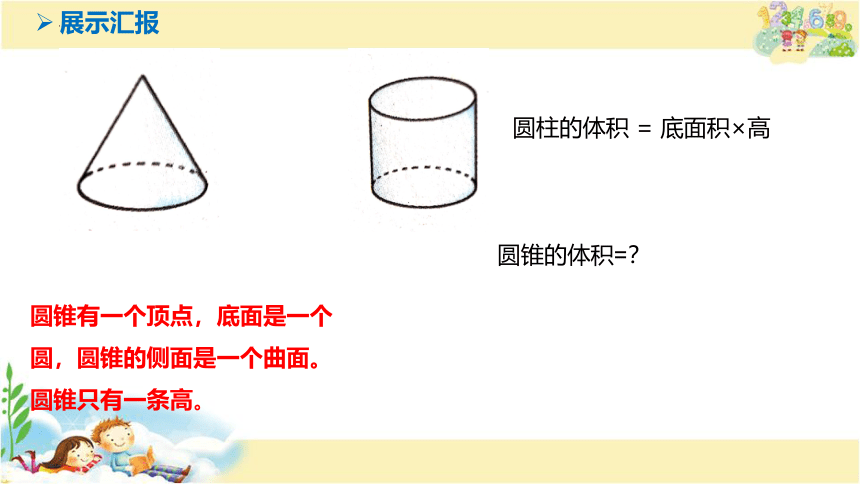
展示汇报
圆锥有一个顶点,底面是一个
圆,圆锥的侧面是一个曲面。
圆锥只有一条高。
圆柱的体积 = 底面积×高
圆锥的体积=?
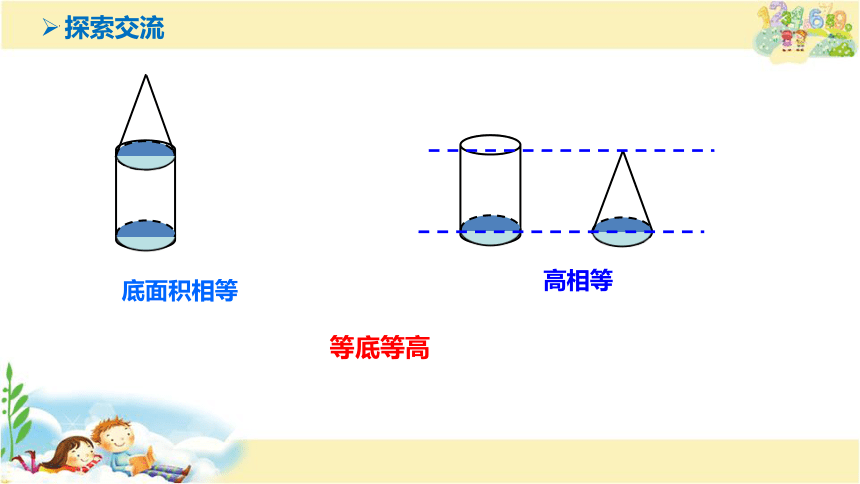
展示汇报
底面积相等
高相等
等底等高
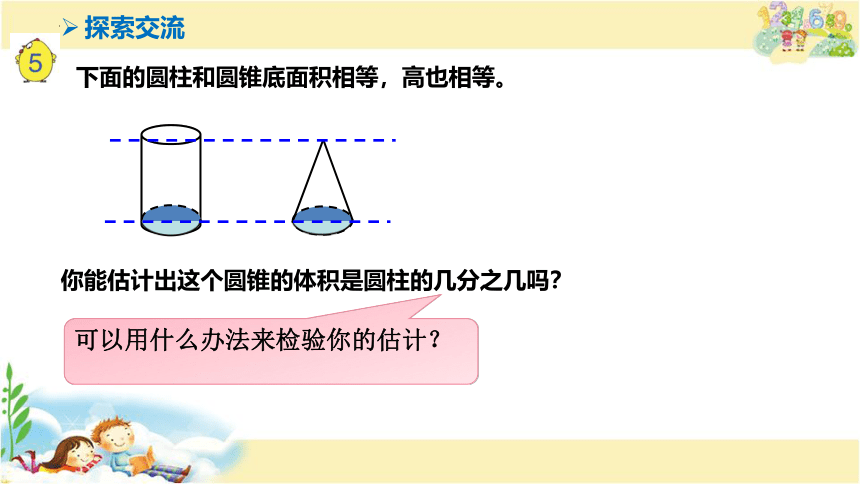
探索交流
下面的圆柱和圆锥底面积相等,高也相等。
你能估计出这个圆锥的体积是圆柱的几分之几吗?
可以用什么办法来检验你的估计?
探索交流
圆锥与它等底等高的圆柱体积关系演示图(认真观察两者的关系)
探索交流
下面的圆柱和圆锥底面积相等,高也相等。
圆锥的体积是与它等底等高
的圆柱体积的
1
3
圆柱的体积是与它等底等高的圆锥体积的3倍。
精讲点拨
圆锥的体积=底面积×高 ×
1
3
1
3
V = sh
精讲点拨
归纳总结
1
3
V = sh
=
×
170
×
12
=680(立方厘米)
基础练习
答:这个零件的体积是680立方厘米。
9.42÷3=3.14(立方厘米)
9.42×3=28.26(立方厘米)
基础练习
第一关:计算圆锥的体积。(单位:cm)
× π×22×6 = 8π(立方厘米)
× π×(3÷2)2×3 = 2.25π(立方厘米)
巩固应用
(1) ×15×10 =40(平方厘米)
(2) × π ×32×5 =15π(平方分米)
(3) × π × (0.4÷2)2×0.6 =0.008π(平方米)
第二关:
巩固应用
(1) π ×32 =9π(平方米)
(2) × π × 32 ×2.4 =7.2π(平方米)
第三关:
巩固应用
1.这节课你学会了什么?
2.计算圆锥的体积时要注意什么?
3. 圆锥的体积公式是怎样推导出来的?
回顾反思
长方体的体积=底面积×高
圆柱的体积=底面积×高
1
3
V = sh
圆锥的体积
数学小讲师
一个圆柱形水杯,底面半径是0.4分米,高是1.5分米。这个圆柱形水杯的体积是多少立方分米?
0.42×π×1.5=0.24π(立方分米)
答:个圆柱形水杯的体积是0.24π立方分米。
知识梳理
小组交流:
1.说一说圆锥的特征?
2.猜测:等底等高的圆锥的体积是圆柱体积的几分之几?
3.用什么办法验证你的猜测?
4.圆锥的体积公式是什么?
圆锥有什么特征?
展示汇报
圆锥有一个顶点,底面是一个
圆,圆锥的侧面是一个曲面。
圆锥只有一条高。
圆柱的体积 = 底面积×高
圆锥的体积=?
展示汇报
底面积相等
高相等
等底等高
探索交流
下面的圆柱和圆锥底面积相等,高也相等。
你能估计出这个圆锥的体积是圆柱的几分之几吗?
可以用什么办法来检验你的估计?
探索交流
圆锥与它等底等高的圆柱体积关系演示图(认真观察两者的关系)
探索交流
下面的圆柱和圆锥底面积相等,高也相等。
圆锥的体积是与它等底等高
的圆柱体积的
1
3
圆柱的体积是与它等底等高的圆锥体积的3倍。
精讲点拨
圆锥的体积=底面积×高 ×
1
3
1
3
V = sh
精讲点拨
归纳总结
1
3
V = sh
=
×
170
×
12
=680(立方厘米)
基础练习
答:这个零件的体积是680立方厘米。
9.42÷3=3.14(立方厘米)
9.42×3=28.26(立方厘米)
基础练习
第一关:计算圆锥的体积。(单位:cm)
× π×22×6 = 8π(立方厘米)
× π×(3÷2)2×3 = 2.25π(立方厘米)
巩固应用
(1) ×15×10 =40(平方厘米)
(2) × π ×32×5 =15π(平方分米)
(3) × π × (0.4÷2)2×0.6 =0.008π(平方米)
第二关:
巩固应用
(1) π ×32 =9π(平方米)
(2) × π × 32 ×2.4 =7.2π(平方米)
第三关:
巩固应用
1.这节课你学会了什么?
2.计算圆锥的体积时要注意什么?
3. 圆锥的体积公式是怎样推导出来的?
回顾反思
长方体的体积=底面积×高
圆柱的体积=底面积×高
1
3
V = sh
