正比例和反比例课件(共20张PPT)六年级下册数学 苏教版
文档属性
| 名称 | 正比例和反比例课件(共20张PPT)六年级下册数学 苏教版 |  | |
| 格式 | zip | ||
| 文件大小 | 734.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-29 18:08:13 | ||
图片预览








文档简介
(共20张PPT)
正比例和反比例(1)
知识梳理
小组活动要求:
1.说一说:自己的收获。
2.记一记:用红笔进行补充。
3.想一想:在有疑问的地方做上记号。
什么是比?什么是比的基本性质?
说说用比的知识可以解决哪些实际问题。
什么是比?什么是比的基本性质?
两个数相除又叫作两个数的比。
比的前项和后项同时乘或除以同一个不为0的数,比值不变。
知识梳理
说说用比的知识可以解决哪些实际问题。
如:比赛算比分;
配不同浓度的盐水;
……
知识梳理
根据比和分数、除法的联系填写下面的等式,说说比的基本性质与分数的基本性质、商不变的规律有什么联系。
a
b
a
b
知识梳理
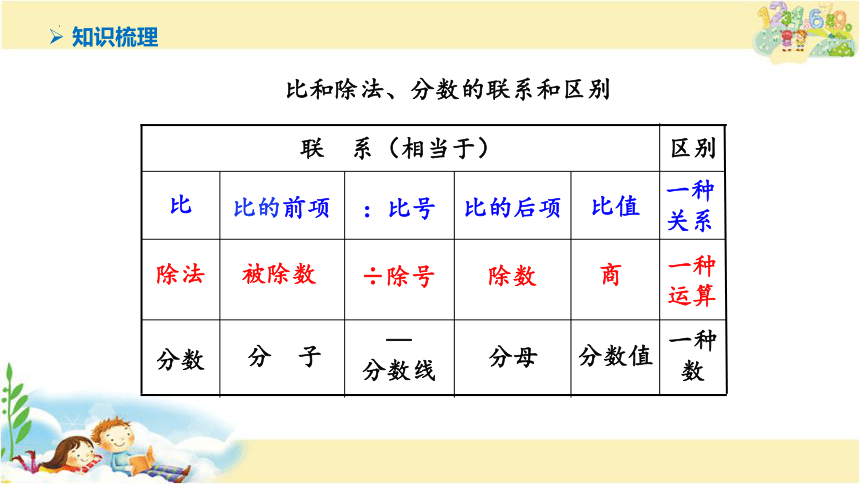
比和除法、分数的联系和区别
分数
除法
比
区别
联 系(相当于)
比的前项
:比号
比的后项
比值
被除数
÷除号
除数
商
分 子
—
分数线
分母
分数值
一种关系
一种运算
一种数
知识梳理
怎样判断两种量是否成正比例关系?
知识梳理
正比例关系的图像有什么特点?
所描的点在同一条直线上
正比例关系用字母表示:
(一定)
两种相关联的量,一种量变化另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就成正比例关系,这两种量是成正比例的量。
怎样判断两种量是否成反比例关系?
知识梳理
反比例关系的图像有什么特点?
两种相关联的量,一种量变化另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就成反比例关系,这两种量是成反比例的量。
反比例关系用字母表示:
(积一定)
反比例关系的图像是一条的曲线。
举出生活中成正比例或反比例的例子,与同学交流。
正比例:
打字速度一定,打字时间与总字数成正比例。
速度一定,时间与路程成正比例。
知识梳理
反比例:
百米赛跑,路程100米不变,速度和时间是反比例。
排队做操,总人数不变,排队的行数和每行的人数成反比例。
……
1.(1)六年级一班有男生23 人,女生24人。男、女生人数的
比是( ), 女生与全班人数的比是( )。
(2)一辆汽车5小时行驶 240千米。这辆汽车行驶的路程与时
间的比是( ),行驶的时间与路程的比是( )。
(3)配制一种盐水,盐和水质量的比是 1︰24, 盐和盐水质
量的比是( ),水和盐水质量的比是( )。
23︰24
24︰47
48︰1
1︰48
1︰25
24︰25
练习与实践
1.(4)公鸡与母鸡只数的比是3︰7 ,公鸡占总只数的 ,
母鸡占总只数的 。
( )
( )
( )
( )
3
10
7
10
练习与实践
2.
(1)量出每幅图片的长和宽, 并写出长和宽的比。
3.9︰2.7
2.6︰0.8
1.7︰1.7
1.3︰0.9
(2)先估计哪两个比能组成比例,再算一算,看估计得对不对。
练习与实践
2.
(2)先估计哪两个比能组成比例,再算一算,看估计得对不对。
3.9︰2.7=1.3︰0.9
答:第一幅图片和第四幅图片的比能组成比例。
练习与实践
3. 解比例。
9︰5 = 4.5︰x
︰x = ︰
解:9x = 5×4.5
9x = 22.5
x = 2.5
解:0.4x = 28×0.1
0.4x = 2.8
x = 7
解: x = ×
x =
x =
练习与实践
4.下表是我国东、西部地区各类土地资源面积分别占全国同类
土地资源总面积的百分数。
(1)我国的耕地大部分在东部地区还是西部地区?林地呢?
(2)写出东部地区和西部地区耕地面积的比。
(3)从表中还能获得哪些信息? 你还能提出哪些问题?
练习与实践
5.一个房间的地面由两种颜色的地砖铺成 (如下图)。
(1)写出两种地砖铺地面积的比,
并化简。
答:深色地砖与浅色地砖铺地面积的比是 1︰2。
20︰40=1︰2
练习与实践
5.一个房间的地面由两种颜色的地砖铺成 (如下图)。
(1)写出两种地砖铺地面积的比,
并化简。
(2)如果这个房间的面积是 15 平
方米,两种地砖的铺地面积分
别是多少平方米?
15÷(1+2)
=15÷3
=5(平方米)
15-5=10(平方米)
答:深度地砖的铺地面积是5平方米,
浅色地砖的铺地面积是10平方米。
练习与实践
6.分别量出学校到市民广场、少年宫、体育场和火车站的图上
距离,再根据比例尺算出它们的实际距离。
3cm
4cm
6cm
3cm
600×3=1800(米) 600×4=2400(米) 600×6=3600(米)
答:学校到市民广场的实际距离是1800米,到少年宫的实际距离是2400
米,到体育场的实际距离是1800米,到火车站的实际距离是3600米。
练习与实践
拓展与应用
实验小学六(1)班一共有45名学生,该班男、女生
人数的比不可能是( )。
A. 2:3 B. 4:5 C. 3:2 D. 3:5
D
通过这节课的学习活动,你有什么收获?
回顾与反思
正比例和反比例(1)
知识梳理
小组活动要求:
1.说一说:自己的收获。
2.记一记:用红笔进行补充。
3.想一想:在有疑问的地方做上记号。
什么是比?什么是比的基本性质?
说说用比的知识可以解决哪些实际问题。
什么是比?什么是比的基本性质?
两个数相除又叫作两个数的比。
比的前项和后项同时乘或除以同一个不为0的数,比值不变。
知识梳理
说说用比的知识可以解决哪些实际问题。
如:比赛算比分;
配不同浓度的盐水;
……
知识梳理
根据比和分数、除法的联系填写下面的等式,说说比的基本性质与分数的基本性质、商不变的规律有什么联系。
a
b
a
b
知识梳理
比和除法、分数的联系和区别
分数
除法
比
区别
联 系(相当于)
比的前项
:比号
比的后项
比值
被除数
÷除号
除数
商
分 子
—
分数线
分母
分数值
一种关系
一种运算
一种数
知识梳理
怎样判断两种量是否成正比例关系?
知识梳理
正比例关系的图像有什么特点?
所描的点在同一条直线上
正比例关系用字母表示:
(一定)
两种相关联的量,一种量变化另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就成正比例关系,这两种量是成正比例的量。
怎样判断两种量是否成反比例关系?
知识梳理
反比例关系的图像有什么特点?
两种相关联的量,一种量变化另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就成反比例关系,这两种量是成反比例的量。
反比例关系用字母表示:
(积一定)
反比例关系的图像是一条的曲线。
举出生活中成正比例或反比例的例子,与同学交流。
正比例:
打字速度一定,打字时间与总字数成正比例。
速度一定,时间与路程成正比例。
知识梳理
反比例:
百米赛跑,路程100米不变,速度和时间是反比例。
排队做操,总人数不变,排队的行数和每行的人数成反比例。
……
1.(1)六年级一班有男生23 人,女生24人。男、女生人数的
比是( ), 女生与全班人数的比是( )。
(2)一辆汽车5小时行驶 240千米。这辆汽车行驶的路程与时
间的比是( ),行驶的时间与路程的比是( )。
(3)配制一种盐水,盐和水质量的比是 1︰24, 盐和盐水质
量的比是( ),水和盐水质量的比是( )。
23︰24
24︰47
48︰1
1︰48
1︰25
24︰25
练习与实践
1.(4)公鸡与母鸡只数的比是3︰7 ,公鸡占总只数的 ,
母鸡占总只数的 。
( )
( )
( )
( )
3
10
7
10
练习与实践
2.
(1)量出每幅图片的长和宽, 并写出长和宽的比。
3.9︰2.7
2.6︰0.8
1.7︰1.7
1.3︰0.9
(2)先估计哪两个比能组成比例,再算一算,看估计得对不对。
练习与实践
2.
(2)先估计哪两个比能组成比例,再算一算,看估计得对不对。
3.9︰2.7=1.3︰0.9
答:第一幅图片和第四幅图片的比能组成比例。
练习与实践
3. 解比例。
9︰5 = 4.5︰x
︰x = ︰
解:9x = 5×4.5
9x = 22.5
x = 2.5
解:0.4x = 28×0.1
0.4x = 2.8
x = 7
解: x = ×
x =
x =
练习与实践
4.下表是我国东、西部地区各类土地资源面积分别占全国同类
土地资源总面积的百分数。
(1)我国的耕地大部分在东部地区还是西部地区?林地呢?
(2)写出东部地区和西部地区耕地面积的比。
(3)从表中还能获得哪些信息? 你还能提出哪些问题?
练习与实践
5.一个房间的地面由两种颜色的地砖铺成 (如下图)。
(1)写出两种地砖铺地面积的比,
并化简。
答:深色地砖与浅色地砖铺地面积的比是 1︰2。
20︰40=1︰2
练习与实践
5.一个房间的地面由两种颜色的地砖铺成 (如下图)。
(1)写出两种地砖铺地面积的比,
并化简。
(2)如果这个房间的面积是 15 平
方米,两种地砖的铺地面积分
别是多少平方米?
15÷(1+2)
=15÷3
=5(平方米)
15-5=10(平方米)
答:深度地砖的铺地面积是5平方米,
浅色地砖的铺地面积是10平方米。
练习与实践
6.分别量出学校到市民广场、少年宫、体育场和火车站的图上
距离,再根据比例尺算出它们的实际距离。
3cm
4cm
6cm
3cm
600×3=1800(米) 600×4=2400(米) 600×6=3600(米)
答:学校到市民广场的实际距离是1800米,到少年宫的实际距离是2400
米,到体育场的实际距离是1800米,到火车站的实际距离是3600米。
练习与实践
拓展与应用
实验小学六(1)班一共有45名学生,该班男、女生
人数的比不可能是( )。
A. 2:3 B. 4:5 C. 3:2 D. 3:5
D
通过这节课的学习活动,你有什么收获?
回顾与反思
