直线和抛物线的关系[上学期]
图片预览



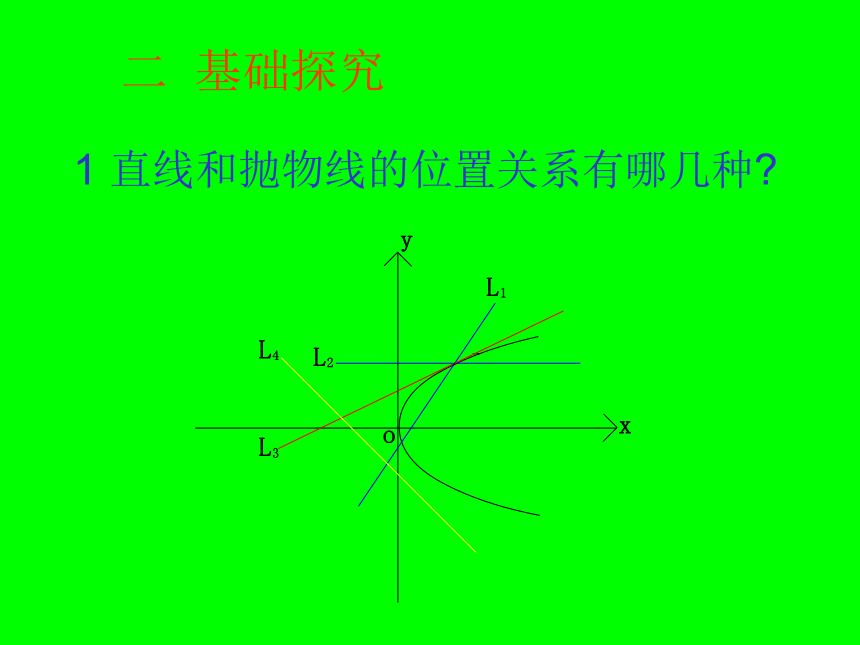



文档简介
课件14张PPT。一复习引入
1 直线和双曲线的位置关系有哪几种?
直线和双曲线有两个公共点,或一 个公共点
相切: 相离:相交:直线和双曲线有且只有一个公共点,且直线和双曲线的渐近线不平行也不重合.
直线和双曲线没有公共点.
直线和抛物线的位置关系学习目标
1熟练掌握直线与抛物线位置关系判定方法
2进一步掌握数形结合的思想方法
二 基础探究1 直线和抛物线的位置关系有哪几种?2 直线和抛物线方程联立的方程组 解的个数与位置关系方程组两组解相交方程组没有解相离方程组一组解相切 若消元得到一次方程,则方程组只有一组解,直线和抛物线的对称轴平行或重合,为相交关系.若消元得到二次方程,则 例1 求过定点P(0,1)且与抛物线
只有一个公共点的直线的方程.由{ 得 {故直线 x=0与抛物线只有一个交点. 解: (1)若直线斜率不存在,则过点P的直线方程是 x=0.
由方程组 { 消去 y 得
(2)若直线斜率存在,设为k,则过P点的直线方程是y=kx+1,三 知识运用与解题研究 当 k=0时,x= ,y=1.
故直线 y=1 与抛物线只有一个交点 .当k≠0时,若直线与抛物线只有一个公共点,则此时直线方程为综上所述,所求直线方程是 x=0 或 y=1 或 点评:本题用了分类讨论的方法.若先用数形结合,找出符合条件的直线的条数,就不会造成漏解。 例2 在抛物线 上求一点,使它到直线 2x-y-4=0的距离最小. 解:设P(x,y)为抛物线 上任意一点,则P到直线2x-y-4=0的距离 此时 y=1,所求点的坐标为P(1,1).当且仅当 x=1 时, , 另解: 观察图象可知,平移直线至与抛物线相切,则切点
即为所求. 联立 得 设切线方程为 2x-y+C=0,由 得 C=-1又由( )得 x=1,∴y=1.故所求点的坐标是(1,1).点评:此处用到了数形结合的方法.三 练习研究 1 当b为何值时,直线y= -2x+b与抛物线(1)相交,(2)相切,(3)相离?
解:由方程组{ 消去 y ,并整理得(1)当 即b>-2时,直线与抛物线相交 (2)当 即b=-2时,直线与抛物线相切 (2)当即(3)当 即b<-2时,直线与抛物线相离 2.过点(0,2)与抛物线 只有一个公共点的直线有( )
(A)1条 (B)2条 (C)3条 (D)无数多条 C 3 倾斜角为600的直线经过抛物线 的焦点 且与抛物线相交于A,B两点,求下列问题: c︱AB︳=_____________S?AOB=__________XA+XB=___________AB中点C的纵坐标YC=_____sin∠A′FB′=______ .1 直线和抛物线方程联立的方程组 解的个数与位置关系方程组两组解相交方程组没有解相离方程组一组解相切 若消元得到一次方程,则方程组只有一组解,直线和抛物线的对称轴平行或重合,为相交关系.若消元得到二次方程,则课堂小结课堂小结 2 方程组的解恰好反映了曲线交点情形, 注意两者相互结合
3 数形结合是解析几何中重要的方法
相切: 相离:相交:直线和双曲线有且只有一个公共点,且直线和双曲线的渐近线不平行也不重合.
直线和双曲线没有公共点.
直线和抛物线的位置关系学习目标
1熟练掌握直线与抛物线位置关系判定方法
2进一步掌握数形结合的思想方法
二 基础探究1 直线和抛物线的位置关系有哪几种?2 直线和抛物线方程联立的方程组 解的个数与位置关系方程组两组解相交方程组没有解相离方程组一组解相切 若消元得到一次方程,则方程组只有一组解,直线和抛物线的对称轴平行或重合,为相交关系.若消元得到二次方程,则 例1 求过定点P(0,1)且与抛物线
只有一个公共点的直线的方程.由{ 得 {故直线 x=0与抛物线只有一个交点. 解: (1)若直线斜率不存在,则过点P的直线方程是 x=0.
由方程组 { 消去 y 得
(2)若直线斜率存在,设为k,则过P点的直线方程是y=kx+1,三 知识运用与解题研究 当 k=0时,x= ,y=1.
故直线 y=1 与抛物线只有一个交点 .当k≠0时,若直线与抛物线只有一个公共点,则此时直线方程为综上所述,所求直线方程是 x=0 或 y=1 或 点评:本题用了分类讨论的方法.若先用数形结合,找出符合条件的直线的条数,就不会造成漏解。 例2 在抛物线 上求一点,使它到直线 2x-y-4=0的距离最小. 解:设P(x,y)为抛物线 上任意一点,则P到直线2x-y-4=0的距离 此时 y=1,所求点的坐标为P(1,1).当且仅当 x=1 时, , 另解: 观察图象可知,平移直线至与抛物线相切,则切点
即为所求. 联立 得 设切线方程为 2x-y+C=0,由 得 C=-1又由( )得 x=1,∴y=1.故所求点的坐标是(1,1).点评:此处用到了数形结合的方法.三 练习研究 1 当b为何值时,直线y= -2x+b与抛物线(1)相交,(2)相切,(3)相离?
解:由方程组{ 消去 y ,并整理得(1)当 即b>-2时,直线与抛物线相交 (2)当 即b=-2时,直线与抛物线相切 (2)当即(3)当 即b<-2时,直线与抛物线相离 2.过点(0,2)与抛物线 只有一个公共点的直线有( )
(A)1条 (B)2条 (C)3条 (D)无数多条 C 3 倾斜角为600的直线经过抛物线 的焦点 且与抛物线相交于A,B两点,求下列问题: c︱AB︳=_____________S?AOB=__________XA+XB=___________AB中点C的纵坐标YC=_____sin∠A′FB′=______ .1 直线和抛物线方程联立的方程组 解的个数与位置关系方程组两组解相交方程组没有解相离方程组一组解相切 若消元得到一次方程,则方程组只有一组解,直线和抛物线的对称轴平行或重合,为相交关系.若消元得到二次方程,则课堂小结课堂小结 2 方程组的解恰好反映了曲线交点情形, 注意两者相互结合
3 数形结合是解析几何中重要的方法
