苏教版(2019)高中数学选择性必修第一册 第4章 数列复习课 学案(含解析)
文档属性
| 名称 | 苏教版(2019)高中数学选择性必修第一册 第4章 数列复习课 学案(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 919.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 09:18:43 | ||
图片预览




文档简介
§4 数列复习课
目标要求
1、理解并掌握等差数列与等比数列的基本运算.
2、理解并掌握等差、等比数列的性质及应用.
3、理解并掌握数列的通项与求和.
4、理解并掌握等差、等比数列的判定.
5、理解与掌握数列与函数.
学科素养目标
在数学中,数列的内容涉及函数、极限、级数等,它实际上是联系初等数学与高等数学的桥梁.由于数列在日常生活中广泛的应用性,以及数列在今后进一步学习数学中的基础性,奠定了本章内容在数学教学中的重要地位.
本章教材的设计,注意体现学生是学习的主体的思想.在给出大量的生活实例之后,给学生一定的思考和探索空间,促使教学方式和学习方式的改变.让学生通过观察、操作、归纳、猜想、验证、推理、讨论和交流体验数学;在习题中设置了“探究·拓展”栏目,为学有余力的学生提供一些富有挑战性的问题,进一步激发学习兴趣,拓宽视野,提高数学素养;教材设置了旁白、思考、阅读、链接等内容,为学生主动探究数学知识的产生和发展提供了空间.
重点难点
重点:等差、等比数列的判定;
难点:数列与函数.
教学过程
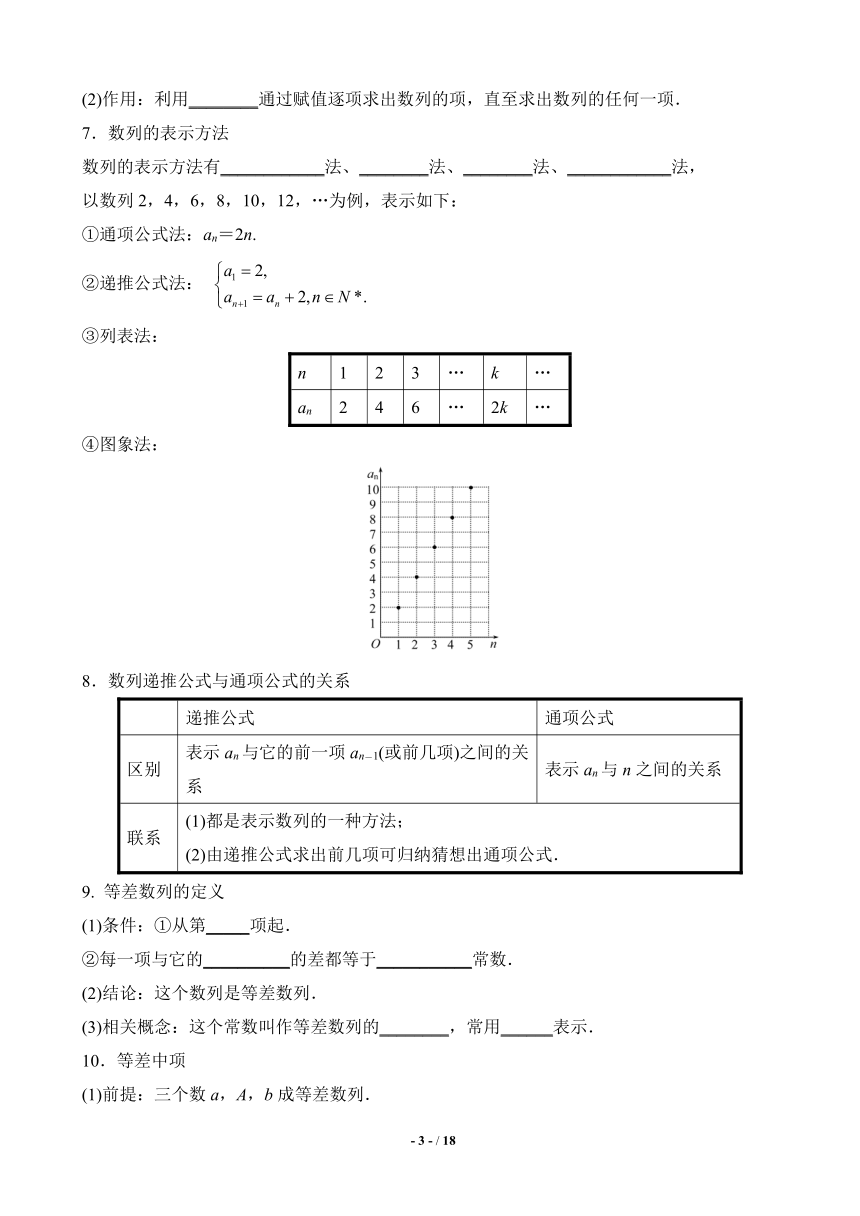
思维结构简图
基础知识积累
1. 数列的有关概念
数列 按照_____________排列的一列数称为数列
项 数列中的__________都叫作这个数列的项
首项 数列的第____项称为首项
2.数列的表示
①一般形式:;
②字母表示:上面数列通常记为.
3.数列的分类
类别 含义
按项数 有穷数列 项数________的数列
无穷数列 项数________的数列
按项的变化趋势 递增数列 从第2项起,每一项都________它的前一项的数列
递减数列 从第2项起,每一项都________它的前一项的数列
常数列 各项都________的数列
摆动数列 从第2项起,有些项________它的前一项,有些项________它的前一项的数列
4.数列的通项公式
一般地,如果数列的第项与序号之间的关系可以用一个公式来表示,那么这个公式叫作这个数列的通项公式.
5.数列与函数的关系
从函数的观点看,数列可以看作是特殊的函数,它们的关系如下表:
定义域 正整数集N*(或它的有限子集{1,2,3,…,})
解析式 数列的通项公式
值域 自变量从小到大依次取值时对应的一列函数值构成
表示方法 (1)__________(解析法);(2)________;(3)_______
6. 递推公式
(1)概念:如果已知一个数列{an}的第1项(或前几项),且任一项an与它的前一项an-1(或前几项)间的关系可以用一个________来表示,那么这个________叫作这个数列的递推公式.
(2)作用:利用________通过赋值逐项求出数列的项,直至求出数列的任何一项.
7.数列的表示方法
数列的表示方法有____________法、________法、________法、____________法,
以数列2,4,6,8,10,12,…为例,表示如下:
①通项公式法:an=2n.
②递推公式法:
③列表法:
n 1 2 3 … k …
an 2 4 6 … 2k …
④图象法:
8.数列递推公式与通项公式的关系
递推公式 通项公式
区别 表示an与它的前一项an-1(或前几项)之间的关系 表示an与n之间的关系
联系 (1)都是表示数列的一种方法;(2)由递推公式求出前几项可归纳猜想出通项公式.
9. 等差数列的定义
(1)条件:①从第_____项起.
②每一项与它的__________的差都等于___________常数.
(2)结论:这个数列是等差数列.
(3)相关概念:这个常数叫作等差数列的________,常用______表示.
10.等差中项
(1)前提:三个数a,A,b成等差数列.
(2)结论:_______叫作a与b的等差中项.
(3)满足的关系式:2A=_______.
11.等差数列的通项公式
递推公式 通项公式
____________=d(n∈N*) an=____________(n∈N*)
12. 等差数列的前n项和公式
已知量 首项,末项与项数 首项,公差与项数
求和公式 Sn=_____________ Sn=_________________
在等差数列{an}中,an=a1+(n-1)d,Sn=或Sn=na1+d.涉及a1,d,n,an及Sn五个基本量,它们分别表示等差数列的首项,公差,项数,项和前n项和.依据方程的思想,在等差数列前n项和公式中已知其中三个量可求另外两个量,即“知三求二”.
13.等差数列的前n项和公式与二次函数的关系
将等差数列前n项和公式Sn=na1+d整理成关于n的函数可得Sn=____n2+________n.
14. 等比数列
一般地,如果一个数列从第二项起,每一项与它的__________的比都等于__________常数,那么这个数列就叫作等比数列,这个常数叫作等比数列的________,公比通常用字母____表示.
15.等比中项
在a与b中间插入一个数G,使a,G,b成____________,那么G叫作a与b的等比中项.
16.等比数列的通项公式
首项为a1,公比是q(q≠0)的等比数列的通项公式为_____________.
17. 等比数列的前n项和公式
已知量 首项、公比与项数 首项、公比与末项
求和公式 Sn=________________________ Sn=_______________________
18.错位相减法
(1)推导等比数列前n项和的方法叫________________.
(2)该方法一般适用于求一个等差数列与一个等比数列_______________的前n项和,即若{bn}是公差d≠0的等差数列,{cn}是公比q≠1的等比数列,求数列{bn·cn}的前n项和Sn时,可以用这种方法.
【课堂题组训练】
题组训练一 等差数列与等比数列的基本运算
题1.在等比数列{an}中,Sn是它的前n项和,若a2·a3=2a1,且a4与2a7的等差中项为17,则S6=( )
A. B.16 C.15 D.
题2.已知等差数列{an}的前n项和为Sn,且a3+a8=13,S7=35,则a7=________.
题3.已知等差数列{an}的公差不为零,a1=25,且a1,a11,a13成等比数列.
(1)求{an}的通项公式;
(2)求a1+a4+a7+…+a3n-2.
题组训练二 等差、等比数列的性质及应用
题4.已知{an}为等差数列,a1+a3+a5=105,a2+a4+a6=99,以Sn表示数列{an}的前n项和,则使得Sn取得最大值的n是 ( )
A.21 B.20 C.19 D.18
题5.等差数列{an}中,3(a3+a5)+2(a7+a10+a13)=24,则该数列的前13项和为 ( )
A.13 B.26 C.52 D.156
题6.已知等比数列{an}满足an>0,n=1,2,…,且a5·a2n-5=22n(n≥3),则log2a1+log2a3+…+log2a2n-1等于 ( )
A.n(2n-1) B.(n+1)2 C.n2 D.(n-1)2
题组训练三 数列的通项与求和
题7.已知数列{an}中,a1=1,an+1=an(1-nan+1),则数列{an}的通项公式为 ( )
A.an= B.an= C.an= D.an=
题8.已知数列满足:a1=,,用表示不超过x的最大整数,则的值等于 ( )
A.1 B.2 C.3 D.4
题9.谈祥柏先生是我国著名的数学科普作家,在他的《好玩的数学》一书中,有一篇文章《五分钟挑出埃及分数》,文章告诉我们,古埃及人喜欢使用分子为1的分数(称为埃及分数).则下列埃及分数,,,…,的和是 ( )
A. B. C. D.
题10.已知a1+2a2+22a3+…+2n-1an=9-6n,则数列{an}的通项公式是________.
题组训练四 等差、等比数列的判定
题11.数列{an}的前n项和为Sn,a1=1,Sn+1=4an+2(n∈N*).
(1)设bn=an+1-2an,求证:{bn}是等比数列.
(2)设cn=,求证:{cn}是等差数列.
题12.设Sn为数列{an}的前n项和,对任意的n∈N*,都有Sn=2-an,
数列{bn}满足b1=2a1,bn=(n≥2,n∈N*).
(1)求证:数列{an}是等比数列,并求{an}的通项公式;
(2)判断数列是等差数列还是等比数列,并求数列{bn}的通项公式.
题组训练五 数列与函数
题13.若数列{an}的前n项和Sn=n2-n(n=1,2,3,…),则此数列的通项公式为__________;数列{nan}中数值最小的项是第________项.
题14.若数列{an}的通项公式为an=n2+λn,且{an}是递增数列,则实数λ的取值范围是________.
题15.设数列{an},{bn}满足a1=b1=6,a2=b2=4,a3=b3=3,若{an+1-an}是等差数列,
{bn+1-bn}是等比数列.
(1)分别求出数列{an},{bn}的通项公式;
(2)求数列{an}中最小项及最小项的值.
§4 数列复习课
目标要求
1、理解并掌握等差数列与等比数列的基本运算.
2、理解并掌握等差、等比数列的性质及应用.
3、理解并掌握数列的通项与求和.
4、理解并掌握等差、等比数列的判定.
5、理解与掌握数列与函数.
学科素养目标
在数学中,数列的内容涉及函数、极限、级数等,它实际上是联系初等数学与高等数学的桥梁.由于数列在日常生活中广泛的应用性,以及数列在今后进一步学习数学中的基础性,奠定了本章内容在数学教学中的重要地位.
本章教材的设计,注意体现学生是学习的主体的思想.在给出大量的生活实例之后,给学生一定的思考和探索空间,促使教学方式和学习方式的改变.让学生通过观察、操作、归纳、猜想、验证、推理、讨论和交流体验数学;在习题中设置了“探究·拓展”栏目,为学有余力的学生提供一些富有挑战性的问题,进一步激发学习兴趣,拓宽视野,提高数学素养;教材设置了旁白、思考、阅读、链接等内容,为学生主动探究数学知识的产生和发展提供了空间.
重点难点
重点:等差、等比数列的判定;
难点:数列与函数.
教学过程
思维结构简图
基础知识积累
1. 数列的有关概念
数列 按照 一定次序 排列的一列数称为数列
项 数列中的 每个数 都叫作这个数列的项
首项 数列的第 1 项称为首项
2.数列的表示
①一般形式:;
②字母表示:上面数列通常记为.
3.数列的分类
类别 含义
按项数 有穷数列 项数 有限 的数列
无穷数列 项数 无限 的数列
按项的变化趋势 递增数列 从第2项起,每一项都 大于 它的前一项的数列
递减数列 从第2项起,每一项都 小于 它的前一项的数列
常数列 各项都 相等 的数列
摆动数列 从第2项起,有些项 大于 它的前一项,有些项 小于 它的前一项的数列
4.数列的通项公式
一般地,如果数列的第项与序号之间的关系可以用一个公式来表示,那么这个公式叫作这个数列的通项公式.
5.数列与函数的关系
从函数的观点看,数列可以看作是特殊的函数,它们的关系如下表:
定义域 正整数集N*(或它的有限子集{1,2,3,…,})
解析式 数列的通项公式
值域 自变量从小到大依次取值时对应的一列函数值构成
表示方法 (1) 通项公式 (解析法);(2) 列表法 ;(3) 图象法
6. 递推公式
(1)概念:如果已知一个数列{an}的第1项(或前几项),且任一项an与它的前一项an-1(或前几项)间的关系可以用一个 公式 来表示,那么这个 公式 叫作这个数列的递推公式.
(2)作用:利用 递推公式 通过赋值逐项求出数列的项,直至求出数列的任何一项.
7.数列的表示方法
数列的表示方法有 通项公式 法、 图象 法、 列表 法、 递推公式 法,
以数列2,4,6,8,10,12,…为例,表示如下:
①通项公式法:an=2n.
②递推公式法:
③列表法:
n 1 2 3 … k …
an 2 4 6 … 2k …
④图象法:
8.数列递推公式与通项公式的关系
递推公式 通项公式
区别 表示an与它的前一项an-1(或前几项)之间的关系 表示an与n之间的关系
联系 (1)都是表示数列的一种方法;(2)由递推公式求出前几项可归纳猜想出通项公式.
9. 等差数列的定义
(1)条件:①从第 2 项起.
②每一项与它的 前一项 的差都等于 同一个 常数.
(2)结论:这个数列是等差数列.
(3)相关概念:这个常数叫作等差数列的 公差 ,常用 d 表示.
10.等差中项
(1)前提:三个数a,A,b成等差数列.
(2)结论: A 叫作a与b的等差中项.
(3)满足的关系式:2A= a+b .
11.等差数列的通项公式
递推公式 通项公式
__an+1-an =d(n∈N*) an= a1+(n-1)d (n∈N*)
12. 等差数列的前n项和公式
已知量 首项,末项与项数 首项,公差与项数
求和公式 Sn= Sn=na1+d
在等差数列{an}中,an=a1+(n-1)d,Sn=或Sn=na1+d.涉及a1,d,n,an及Sn五个基本量,它们分别表示等差数列的首项,公差,项数,项和前n项和.依据方程的思想,在等差数列前n项和公式中已知其中三个量可求另外两个量,即“知三求二”.
13.等差数列的前n项和公式与二次函数的关系
将等差数列前n项和公式Sn=na1+d整理成关于n的函数可得Sn= n2+ n.
14. 等比数列
一般地,如果一个数列从第二项起,每一项与它的 前一项 的比都等于 同一个 常数,那么这个数列就叫作等比数列,这个常数叫作等比数列的 公比 ,公比通常用字母 q 表示.
15.等比中项
在a与b中间插入一个数G,使a,G,b成 等比数列 ,那么G叫作a与b的等比中项.
16.等比数列的通项公式
首项为a1,公比是q(q≠0)的等比数列的通项公式为 an=a1qn-1 .
17. 等比数列的前n项和公式
已知量 首项、公比与项数 首项、公比与末项
求和公式 Sn= Sn=
18.错位相减法
(1)推导等比数列前n项和的方法叫 错位相减法 .
(2)该方法一般适用于求一个等差数列与一个等比数列 对应项积 的前n项和,即若{bn}是公差d≠0的等差数列,{cn}是公比q≠1的等比数列,求数列{bn·cn}的前n项和Sn时,可以用这种方法.
【课堂题组训练】
题组训练一 等差数列与等比数列的基本运算
题1.在等比数列{an}中,Sn是它的前n项和,若a2·a3=2a1,且a4与2a7的等差中项为17,则S6=( )
A. B.16 C.15 D.
【解析】选A.设{an}的公比为q,则由等比数列的性质知,a2a3=a1a4=2a1,
则a4=2;由a4与2a7的等差中项为17知,a4+2a7=2×17=34,得a7=16.
所以q3==8,即q=2,所以a1==,则S6==.
题2.已知等差数列{an}的前n项和为Sn,且a3+a8=13,S7=35,则a7=________.
【解析】设等差数列{an}的公差为d,则由已知得(a1+2d)+(a1+7d)=13,
S7==35.联立两式,解得a1=2,d=1,所以a7=a1+6d=8.
答案:8
题3.已知等差数列{an}的公差不为零,a1=25,且a1,a11,a13成等比数列.
(1)求{an}的通项公式;
(2)求a1+a4+a7+…+a3n-2.
【解析】(1)设{an}的公差为d.由题意,得a=a1a13,即(a1+10d)2=a1(a1+12d).
于是d(2a1+25d)=0.又a1=25,所以d=-2或0(舍去).故an=-2n+27.
(2)令Sn=a1+a4+a7+…+a3n-2.由(1)知a3n-2=-6n+31,故{a3n-2}是首项为25,公差为-6的等差数列.
从而Sn=(a1+a3n-2)=(-6n+56)=-3n2+28n.
【解题策略提醒】
等差与等比数列的基本量计算方法
在等差(或等比)数列中,首项a1与公差d(或公比q)是两个基本量,一般的等差(或等比)数列的计算问题,都可以设出这两个量求解.在等差数列中的五个量a1,d,n,an,Sn或等比数列中的五个量a1,q,n,an,Sn中,可通过列方程组的方法,知三求二.在利用Sn求an时,要注意验证n=1是否成立.
题组训练二 等差、等比数列的性质及应用
题4.已知{an}为等差数列,a1+a3+a5=105,a2+a4+a6=99,以Sn表示数列{an}的前n项和,则使得Sn取得最大值的n是 ( )
A.21 B.20 C.19 D.18
【解析】选B.由a1+a3+a5=105得,3a3=105,所以a3=35.同理可得a4=33,
所以d=a4-a3=-2,an=a4+(n-4)×(-2)=41-2n.
由得n=20.所以使Sn达到最大值的n是20.
题5.等差数列{an}中,3(a3+a5)+2(a7+a10+a13)=24,则该数列的前13项和为 ( )
A.13 B.26 C.52 D.156
【解析】选B.3(a3+a5)+2(a7+a10+a13)=24,所以6a4+6a10=24,所以a4+a10=4,
所以S13====26.
题6.已知等比数列{an}满足an>0,n=1,2,…,且a5·a2n-5=22n(n≥3),则log2a1+log2a3+…+log2a2n-1等于 ( )
A.n(2n-1) B.(n+1)2 C.n2 D.(n-1)2
【解析】选C.因为a5·a2n-5=a=22n,且an>0,所以an=2n,因为a2n-1=,
所以log2a2n-1=2n-1,
所以log2a1+log2a3+…+log2=1+3+5+…+(2n-1)==n2.
【解题策略提醒】
等差与等比数列性质的应用
等差、等比数列的性质主要涉及数列的单调性、最值及其前n项和的性质、利用性质求数列中某一项等,关于等差(比)数列性质的应用问题,可以直接构造关于首项a1和公差d(公比q)的方程或方程组来求解,再根据等差(比)数列的通项公式直接求其值,此解思路简单,但运算过程复杂.
题组训练三 数列的通项与求和
题7.已知数列{an}中,a1=1,an+1=an(1-nan+1),则数列{an}的通项公式为 ( )
A.an= B.an= C.an= D.an=
【解析】选D.原数列递推公式可化为-=n,令bn=,则bn+1-bn=n,
因此bn=(bn-bn-1)+(bn-1-bn-2)+…+(b3-b2)+(b2-b1)+b1
=(n-1)+(n-2)+…+2+1+1=.从而an=.
题8.已知数列满足:a1=,,用表示不超过x的最大整数,则的值等于 ( )
A.1 B.2 C.3 D.4
【解析】选A.由,得=-,
所以++…+=-+-+…+-=-=2-,
由a1=,得a1=,a2=,a3=>1知从a3以后都大于1,
所以∈,所以2-∈,则=1.
题9.谈祥柏先生是我国著名的数学科普作家,在他的《好玩的数学》一书中,有一篇文章《五分钟挑出埃及分数》,文章告诉我们,古埃及人喜欢使用分子为1的分数(称为埃及分数).则下列埃及分数,,,…,的和是 ( )
A. B. C. D.
【解析】选B.因为=,所以+++…+
===.
题10.已知a1+2a2+22a3+…+2n-1an=9-6n,则数列{an}的通项公式是________.
【解析】令Sn=a1+2a2+22a3+…+2n-1an,则Sn=9-6n,当n=1时,a1=S1=3;
当n≥2时·an=Sn-Sn-1=-6,所以an=-.所以通项公式an=
答案:an=
【解题策略提醒】
通项与和的求法
1.由递推公式求数列通项公式时,一是要注意判别类型与方法.二是要注意an的完整表达式,易忽视n=1的情况.常用的数列通项公式的求法有:(1)定义法,即直接利用等差数列或等比数列的定义求通项的方法叫定义法,这种方法适用于已知数列类型的题目.
(2)若已知数列的前n项和Sn与an的关系,求数列{an}的通项an可用公式an=求解.
(3)对于递推公式确定的数列的求解,通常可以通过递推公式的变换,转化为等差数列或等比数列问题,有时也用到一些特殊的转化方法与特殊数列.
2.数列求和时,根据数列通项公式特征选择求和法,尤其是涉及等比数列求和时要注意公比q对Sn的影响.一般常见的求和方法有:
(1)公式法:利用等差数列或等比数列前n项和公式;
(2)分组求和法:把一个数列分成几个可以直接求和的数列;
(3)裂项相消法:有时把一个数列的通项公式分成两项差的形式,相加过程消去中间项,只剩有限项再求和;
(4)错位相减法:适用于一个等差数列和一个等比数列对应项相乘构成的数列求和;
(5)并项求和法:一个数列的前n项和中,可两两结合求解,则称之为并项求和.形如an=(-1)nf(n)类型,可采用两项合并求解.
题组训练四 等差、等比数列的判定
题11.数列{an}的前n项和为Sn,a1=1,Sn+1=4an+2(n∈N*).
(1)设bn=an+1-2an,求证:{bn}是等比数列.
(2)设cn=,求证:{cn}是等差数列.
【证明】(1)an+2=Sn+2-Sn+1=4an+1+2-4an-2=4an+1-4an.
====2.
因为S2=a1+a2=4a1+2,所以a2=5.所以b1=a2-2a1=3.所以数列{bn}是首项为3,公比为2的等比数列.
(2)由(1)知bn=3·2n-1=an+1-2an,所以=3.所以cn+1-cn=3,且c1==2,
所以数列{cn}是等差数列,公差为3,首项为2.
题12.设Sn为数列{an}的前n项和,对任意的n∈N*,都有Sn=2-an,
数列{bn}满足b1=2a1,bn=(n≥2,n∈N*).
(1)求证:数列{an}是等比数列,并求{an}的通项公式;
(2)判断数列是等差数列还是等比数列,并求数列{bn}的通项公式.
【解析】(1)当n=1时,a1=S1=2-a1,解得a1=1;
当n≥2时,an=Sn-Sn-1=an-1-an,即=(n≥2,n∈N*).
所以数列{an}是首项为1,公比为的等比数列,
故数列{an}的通项公式为an=.
(2)因为a1=1,所以b1=2a1=2.因为bn=,所以=+1,即-=1(n≥2).
所以数列是首项为,公差为1的等差数列.所以=+(n-1)·1=,
故数列{bn}的通项公式为bn=.
【解题策略提醒】
等差、等比数列的判断与证明方法
(1)定义法:an+1-an=d(常数) {an}是等差数列;=q(q为常数,q≠0) {an}是等比数列;(2)中项公式法:2an+1=an+an+2 {an}是等差数列;a=an·an+2(an≠0) {an}是等比数列;(3)通项公式法:an=kn+b(k,b是常数) {an}是等差数列;an=c·qn(c,q为非零常数) {an}是等比数列;(4)前n项和公式法:Sn=An2+Bn(A,B为常数,n∈N*) {an}是等差数列;Sn=Aqn-A(A,q为常数,且A≠0,q≠0,q≠1,n∈N*) {an}是等比数列.
提醒:①前两种方法是判定等差、等比数列的常用方法,而后两种方法常用于选择、填空题中的判定.②若要判定一个数列不是等差(比)数列,则只需判定其任意的连续三项不成等差(比)即可.
题组训练五 数列与函数
题13.若数列{an}的前n项和Sn=n2-n(n=1,2,3,…),则此数列的通项公式为__________;数列{nan}中数值最小的项是第________项.
【解析】利用an=求得an=3n-16.则nan=3n2-16n=3,
所以n=3时,nan的值最小.
答案:an=3n-16 3
题14.若数列{an}的通项公式为an=n2+λn,且{an}是递增数列,则实数λ的取值范围是________.
【解析】方法一:an+1-an=(n+1)2+λ(n+1)-(n2+λn)=2n+1+λ,
由于{an}是递增数列,故2n+1+λ>0恒成立,即λ>-2n-1,
又n∈N*,-2n-1≤-3,故λ>-3.
方法二:由于函数y=x2+λx在上单调递增,结合其图象可知,若数列{an}是递增数列,则a2>a1,即22+2λ>1+λ,即λ>-3.
答案:(-3,+∞)
题15.设数列{an},{bn}满足a1=b1=6,a2=b2=4,a3=b3=3,若{an+1-an}是等差数列,{bn+1-bn}是等比数列.
(1)分别求出数列{an},{bn}的通项公式;
(2)求数列{an}中最小项及最小项的值.
【解析】(1)a2-a1=-2,a3-a2=-1,由{an+1-an}成等差数列知其公差为1,
故an+1-an=-2+(n-1)·1=n-3;b2-b1=-2,b3-b2=-1,
由{bn+1-bn}成等比数列知,其公比为,故bn+1-bn=-2·,
an=(an-an-1)+(an-1-an-2)+(an-2-an-3)+…+(a2-a1)+a1
=(n-1)·(-2)+·1+6=-2n+8=,
bn=(bn-bn-1)+(bn-1-bn-2)+(bn-2-bn-3)+…+(b2-b1)+b1=+6=2+23-n.
(2)因为an==2+,
所以n=3或n=4时,an取到最小值,最小值为a3=a4=3.
【解题策略提醒】
函数思想在数列问题中的应用
数列可以看作是定义域为正整数集(或其有限子集{1,2,3,…,n})的特殊函数.运用函数思想去研究数列,就是要借助于函数的单调性、图象和最值等知识解决与数列相关的问题.等差数列与一次函数、等比数列与指数函数有着密切的关系,等差数列前n项和公式与二次函数有密切关系,故可用函数的思想来解决数列问题.
- 1 - / 18
目标要求
1、理解并掌握等差数列与等比数列的基本运算.
2、理解并掌握等差、等比数列的性质及应用.
3、理解并掌握数列的通项与求和.
4、理解并掌握等差、等比数列的判定.
5、理解与掌握数列与函数.
学科素养目标
在数学中,数列的内容涉及函数、极限、级数等,它实际上是联系初等数学与高等数学的桥梁.由于数列在日常生活中广泛的应用性,以及数列在今后进一步学习数学中的基础性,奠定了本章内容在数学教学中的重要地位.
本章教材的设计,注意体现学生是学习的主体的思想.在给出大量的生活实例之后,给学生一定的思考和探索空间,促使教学方式和学习方式的改变.让学生通过观察、操作、归纳、猜想、验证、推理、讨论和交流体验数学;在习题中设置了“探究·拓展”栏目,为学有余力的学生提供一些富有挑战性的问题,进一步激发学习兴趣,拓宽视野,提高数学素养;教材设置了旁白、思考、阅读、链接等内容,为学生主动探究数学知识的产生和发展提供了空间.
重点难点
重点:等差、等比数列的判定;
难点:数列与函数.
教学过程
思维结构简图
基础知识积累
1. 数列的有关概念
数列 按照_____________排列的一列数称为数列
项 数列中的__________都叫作这个数列的项
首项 数列的第____项称为首项
2.数列的表示
①一般形式:;
②字母表示:上面数列通常记为.
3.数列的分类
类别 含义
按项数 有穷数列 项数________的数列
无穷数列 项数________的数列
按项的变化趋势 递增数列 从第2项起,每一项都________它的前一项的数列
递减数列 从第2项起,每一项都________它的前一项的数列
常数列 各项都________的数列
摆动数列 从第2项起,有些项________它的前一项,有些项________它的前一项的数列
4.数列的通项公式
一般地,如果数列的第项与序号之间的关系可以用一个公式来表示,那么这个公式叫作这个数列的通项公式.
5.数列与函数的关系
从函数的观点看,数列可以看作是特殊的函数,它们的关系如下表:
定义域 正整数集N*(或它的有限子集{1,2,3,…,})
解析式 数列的通项公式
值域 自变量从小到大依次取值时对应的一列函数值构成
表示方法 (1)__________(解析法);(2)________;(3)_______
6. 递推公式
(1)概念:如果已知一个数列{an}的第1项(或前几项),且任一项an与它的前一项an-1(或前几项)间的关系可以用一个________来表示,那么这个________叫作这个数列的递推公式.
(2)作用:利用________通过赋值逐项求出数列的项,直至求出数列的任何一项.
7.数列的表示方法
数列的表示方法有____________法、________法、________法、____________法,
以数列2,4,6,8,10,12,…为例,表示如下:
①通项公式法:an=2n.
②递推公式法:
③列表法:
n 1 2 3 … k …
an 2 4 6 … 2k …
④图象法:
8.数列递推公式与通项公式的关系
递推公式 通项公式
区别 表示an与它的前一项an-1(或前几项)之间的关系 表示an与n之间的关系
联系 (1)都是表示数列的一种方法;(2)由递推公式求出前几项可归纳猜想出通项公式.
9. 等差数列的定义
(1)条件:①从第_____项起.
②每一项与它的__________的差都等于___________常数.
(2)结论:这个数列是等差数列.
(3)相关概念:这个常数叫作等差数列的________,常用______表示.
10.等差中项
(1)前提:三个数a,A,b成等差数列.
(2)结论:_______叫作a与b的等差中项.
(3)满足的关系式:2A=_______.
11.等差数列的通项公式
递推公式 通项公式
____________=d(n∈N*) an=____________(n∈N*)
12. 等差数列的前n项和公式
已知量 首项,末项与项数 首项,公差与项数
求和公式 Sn=_____________ Sn=_________________
在等差数列{an}中,an=a1+(n-1)d,Sn=或Sn=na1+d.涉及a1,d,n,an及Sn五个基本量,它们分别表示等差数列的首项,公差,项数,项和前n项和.依据方程的思想,在等差数列前n项和公式中已知其中三个量可求另外两个量,即“知三求二”.
13.等差数列的前n项和公式与二次函数的关系
将等差数列前n项和公式Sn=na1+d整理成关于n的函数可得Sn=____n2+________n.
14. 等比数列
一般地,如果一个数列从第二项起,每一项与它的__________的比都等于__________常数,那么这个数列就叫作等比数列,这个常数叫作等比数列的________,公比通常用字母____表示.
15.等比中项
在a与b中间插入一个数G,使a,G,b成____________,那么G叫作a与b的等比中项.
16.等比数列的通项公式
首项为a1,公比是q(q≠0)的等比数列的通项公式为_____________.
17. 等比数列的前n项和公式
已知量 首项、公比与项数 首项、公比与末项
求和公式 Sn=________________________ Sn=_______________________
18.错位相减法
(1)推导等比数列前n项和的方法叫________________.
(2)该方法一般适用于求一个等差数列与一个等比数列_______________的前n项和,即若{bn}是公差d≠0的等差数列,{cn}是公比q≠1的等比数列,求数列{bn·cn}的前n项和Sn时,可以用这种方法.
【课堂题组训练】
题组训练一 等差数列与等比数列的基本运算
题1.在等比数列{an}中,Sn是它的前n项和,若a2·a3=2a1,且a4与2a7的等差中项为17,则S6=( )
A. B.16 C.15 D.
题2.已知等差数列{an}的前n项和为Sn,且a3+a8=13,S7=35,则a7=________.
题3.已知等差数列{an}的公差不为零,a1=25,且a1,a11,a13成等比数列.
(1)求{an}的通项公式;
(2)求a1+a4+a7+…+a3n-2.
题组训练二 等差、等比数列的性质及应用
题4.已知{an}为等差数列,a1+a3+a5=105,a2+a4+a6=99,以Sn表示数列{an}的前n项和,则使得Sn取得最大值的n是 ( )
A.21 B.20 C.19 D.18
题5.等差数列{an}中,3(a3+a5)+2(a7+a10+a13)=24,则该数列的前13项和为 ( )
A.13 B.26 C.52 D.156
题6.已知等比数列{an}满足an>0,n=1,2,…,且a5·a2n-5=22n(n≥3),则log2a1+log2a3+…+log2a2n-1等于 ( )
A.n(2n-1) B.(n+1)2 C.n2 D.(n-1)2
题组训练三 数列的通项与求和
题7.已知数列{an}中,a1=1,an+1=an(1-nan+1),则数列{an}的通项公式为 ( )
A.an= B.an= C.an= D.an=
题8.已知数列满足:a1=,,用表示不超过x的最大整数,则的值等于 ( )
A.1 B.2 C.3 D.4
题9.谈祥柏先生是我国著名的数学科普作家,在他的《好玩的数学》一书中,有一篇文章《五分钟挑出埃及分数》,文章告诉我们,古埃及人喜欢使用分子为1的分数(称为埃及分数).则下列埃及分数,,,…,的和是 ( )
A. B. C. D.
题10.已知a1+2a2+22a3+…+2n-1an=9-6n,则数列{an}的通项公式是________.
题组训练四 等差、等比数列的判定
题11.数列{an}的前n项和为Sn,a1=1,Sn+1=4an+2(n∈N*).
(1)设bn=an+1-2an,求证:{bn}是等比数列.
(2)设cn=,求证:{cn}是等差数列.
题12.设Sn为数列{an}的前n项和,对任意的n∈N*,都有Sn=2-an,
数列{bn}满足b1=2a1,bn=(n≥2,n∈N*).
(1)求证:数列{an}是等比数列,并求{an}的通项公式;
(2)判断数列是等差数列还是等比数列,并求数列{bn}的通项公式.
题组训练五 数列与函数
题13.若数列{an}的前n项和Sn=n2-n(n=1,2,3,…),则此数列的通项公式为__________;数列{nan}中数值最小的项是第________项.
题14.若数列{an}的通项公式为an=n2+λn,且{an}是递增数列,则实数λ的取值范围是________.
题15.设数列{an},{bn}满足a1=b1=6,a2=b2=4,a3=b3=3,若{an+1-an}是等差数列,
{bn+1-bn}是等比数列.
(1)分别求出数列{an},{bn}的通项公式;
(2)求数列{an}中最小项及最小项的值.
§4 数列复习课
目标要求
1、理解并掌握等差数列与等比数列的基本运算.
2、理解并掌握等差、等比数列的性质及应用.
3、理解并掌握数列的通项与求和.
4、理解并掌握等差、等比数列的判定.
5、理解与掌握数列与函数.
学科素养目标
在数学中,数列的内容涉及函数、极限、级数等,它实际上是联系初等数学与高等数学的桥梁.由于数列在日常生活中广泛的应用性,以及数列在今后进一步学习数学中的基础性,奠定了本章内容在数学教学中的重要地位.
本章教材的设计,注意体现学生是学习的主体的思想.在给出大量的生活实例之后,给学生一定的思考和探索空间,促使教学方式和学习方式的改变.让学生通过观察、操作、归纳、猜想、验证、推理、讨论和交流体验数学;在习题中设置了“探究·拓展”栏目,为学有余力的学生提供一些富有挑战性的问题,进一步激发学习兴趣,拓宽视野,提高数学素养;教材设置了旁白、思考、阅读、链接等内容,为学生主动探究数学知识的产生和发展提供了空间.
重点难点
重点:等差、等比数列的判定;
难点:数列与函数.
教学过程
思维结构简图
基础知识积累
1. 数列的有关概念
数列 按照 一定次序 排列的一列数称为数列
项 数列中的 每个数 都叫作这个数列的项
首项 数列的第 1 项称为首项
2.数列的表示
①一般形式:;
②字母表示:上面数列通常记为.
3.数列的分类
类别 含义
按项数 有穷数列 项数 有限 的数列
无穷数列 项数 无限 的数列
按项的变化趋势 递增数列 从第2项起,每一项都 大于 它的前一项的数列
递减数列 从第2项起,每一项都 小于 它的前一项的数列
常数列 各项都 相等 的数列
摆动数列 从第2项起,有些项 大于 它的前一项,有些项 小于 它的前一项的数列
4.数列的通项公式
一般地,如果数列的第项与序号之间的关系可以用一个公式来表示,那么这个公式叫作这个数列的通项公式.
5.数列与函数的关系
从函数的观点看,数列可以看作是特殊的函数,它们的关系如下表:
定义域 正整数集N*(或它的有限子集{1,2,3,…,})
解析式 数列的通项公式
值域 自变量从小到大依次取值时对应的一列函数值构成
表示方法 (1) 通项公式 (解析法);(2) 列表法 ;(3) 图象法
6. 递推公式
(1)概念:如果已知一个数列{an}的第1项(或前几项),且任一项an与它的前一项an-1(或前几项)间的关系可以用一个 公式 来表示,那么这个 公式 叫作这个数列的递推公式.
(2)作用:利用 递推公式 通过赋值逐项求出数列的项,直至求出数列的任何一项.
7.数列的表示方法
数列的表示方法有 通项公式 法、 图象 法、 列表 法、 递推公式 法,
以数列2,4,6,8,10,12,…为例,表示如下:
①通项公式法:an=2n.
②递推公式法:
③列表法:
n 1 2 3 … k …
an 2 4 6 … 2k …
④图象法:
8.数列递推公式与通项公式的关系
递推公式 通项公式
区别 表示an与它的前一项an-1(或前几项)之间的关系 表示an与n之间的关系
联系 (1)都是表示数列的一种方法;(2)由递推公式求出前几项可归纳猜想出通项公式.
9. 等差数列的定义
(1)条件:①从第 2 项起.
②每一项与它的 前一项 的差都等于 同一个 常数.
(2)结论:这个数列是等差数列.
(3)相关概念:这个常数叫作等差数列的 公差 ,常用 d 表示.
10.等差中项
(1)前提:三个数a,A,b成等差数列.
(2)结论: A 叫作a与b的等差中项.
(3)满足的关系式:2A= a+b .
11.等差数列的通项公式
递推公式 通项公式
__an+1-an =d(n∈N*) an= a1+(n-1)d (n∈N*)
12. 等差数列的前n项和公式
已知量 首项,末项与项数 首项,公差与项数
求和公式 Sn= Sn=na1+d
在等差数列{an}中,an=a1+(n-1)d,Sn=或Sn=na1+d.涉及a1,d,n,an及Sn五个基本量,它们分别表示等差数列的首项,公差,项数,项和前n项和.依据方程的思想,在等差数列前n项和公式中已知其中三个量可求另外两个量,即“知三求二”.
13.等差数列的前n项和公式与二次函数的关系
将等差数列前n项和公式Sn=na1+d整理成关于n的函数可得Sn= n2+ n.
14. 等比数列
一般地,如果一个数列从第二项起,每一项与它的 前一项 的比都等于 同一个 常数,那么这个数列就叫作等比数列,这个常数叫作等比数列的 公比 ,公比通常用字母 q 表示.
15.等比中项
在a与b中间插入一个数G,使a,G,b成 等比数列 ,那么G叫作a与b的等比中项.
16.等比数列的通项公式
首项为a1,公比是q(q≠0)的等比数列的通项公式为 an=a1qn-1 .
17. 等比数列的前n项和公式
已知量 首项、公比与项数 首项、公比与末项
求和公式 Sn= Sn=
18.错位相减法
(1)推导等比数列前n项和的方法叫 错位相减法 .
(2)该方法一般适用于求一个等差数列与一个等比数列 对应项积 的前n项和,即若{bn}是公差d≠0的等差数列,{cn}是公比q≠1的等比数列,求数列{bn·cn}的前n项和Sn时,可以用这种方法.
【课堂题组训练】
题组训练一 等差数列与等比数列的基本运算
题1.在等比数列{an}中,Sn是它的前n项和,若a2·a3=2a1,且a4与2a7的等差中项为17,则S6=( )
A. B.16 C.15 D.
【解析】选A.设{an}的公比为q,则由等比数列的性质知,a2a3=a1a4=2a1,
则a4=2;由a4与2a7的等差中项为17知,a4+2a7=2×17=34,得a7=16.
所以q3==8,即q=2,所以a1==,则S6==.
题2.已知等差数列{an}的前n项和为Sn,且a3+a8=13,S7=35,则a7=________.
【解析】设等差数列{an}的公差为d,则由已知得(a1+2d)+(a1+7d)=13,
S7==35.联立两式,解得a1=2,d=1,所以a7=a1+6d=8.
答案:8
题3.已知等差数列{an}的公差不为零,a1=25,且a1,a11,a13成等比数列.
(1)求{an}的通项公式;
(2)求a1+a4+a7+…+a3n-2.
【解析】(1)设{an}的公差为d.由题意,得a=a1a13,即(a1+10d)2=a1(a1+12d).
于是d(2a1+25d)=0.又a1=25,所以d=-2或0(舍去).故an=-2n+27.
(2)令Sn=a1+a4+a7+…+a3n-2.由(1)知a3n-2=-6n+31,故{a3n-2}是首项为25,公差为-6的等差数列.
从而Sn=(a1+a3n-2)=(-6n+56)=-3n2+28n.
【解题策略提醒】
等差与等比数列的基本量计算方法
在等差(或等比)数列中,首项a1与公差d(或公比q)是两个基本量,一般的等差(或等比)数列的计算问题,都可以设出这两个量求解.在等差数列中的五个量a1,d,n,an,Sn或等比数列中的五个量a1,q,n,an,Sn中,可通过列方程组的方法,知三求二.在利用Sn求an时,要注意验证n=1是否成立.
题组训练二 等差、等比数列的性质及应用
题4.已知{an}为等差数列,a1+a3+a5=105,a2+a4+a6=99,以Sn表示数列{an}的前n项和,则使得Sn取得最大值的n是 ( )
A.21 B.20 C.19 D.18
【解析】选B.由a1+a3+a5=105得,3a3=105,所以a3=35.同理可得a4=33,
所以d=a4-a3=-2,an=a4+(n-4)×(-2)=41-2n.
由得n=20.所以使Sn达到最大值的n是20.
题5.等差数列{an}中,3(a3+a5)+2(a7+a10+a13)=24,则该数列的前13项和为 ( )
A.13 B.26 C.52 D.156
【解析】选B.3(a3+a5)+2(a7+a10+a13)=24,所以6a4+6a10=24,所以a4+a10=4,
所以S13====26.
题6.已知等比数列{an}满足an>0,n=1,2,…,且a5·a2n-5=22n(n≥3),则log2a1+log2a3+…+log2a2n-1等于 ( )
A.n(2n-1) B.(n+1)2 C.n2 D.(n-1)2
【解析】选C.因为a5·a2n-5=a=22n,且an>0,所以an=2n,因为a2n-1=,
所以log2a2n-1=2n-1,
所以log2a1+log2a3+…+log2=1+3+5+…+(2n-1)==n2.
【解题策略提醒】
等差与等比数列性质的应用
等差、等比数列的性质主要涉及数列的单调性、最值及其前n项和的性质、利用性质求数列中某一项等,关于等差(比)数列性质的应用问题,可以直接构造关于首项a1和公差d(公比q)的方程或方程组来求解,再根据等差(比)数列的通项公式直接求其值,此解思路简单,但运算过程复杂.
题组训练三 数列的通项与求和
题7.已知数列{an}中,a1=1,an+1=an(1-nan+1),则数列{an}的通项公式为 ( )
A.an= B.an= C.an= D.an=
【解析】选D.原数列递推公式可化为-=n,令bn=,则bn+1-bn=n,
因此bn=(bn-bn-1)+(bn-1-bn-2)+…+(b3-b2)+(b2-b1)+b1
=(n-1)+(n-2)+…+2+1+1=.从而an=.
题8.已知数列满足:a1=,,用表示不超过x的最大整数,则的值等于 ( )
A.1 B.2 C.3 D.4
【解析】选A.由,得=-,
所以++…+=-+-+…+-=-=2-,
由a1=,得a1=,a2=,a3=>1知从a3以后都大于1,
所以∈,所以2-∈,则=1.
题9.谈祥柏先生是我国著名的数学科普作家,在他的《好玩的数学》一书中,有一篇文章《五分钟挑出埃及分数》,文章告诉我们,古埃及人喜欢使用分子为1的分数(称为埃及分数).则下列埃及分数,,,…,的和是 ( )
A. B. C. D.
【解析】选B.因为=,所以+++…+
===.
题10.已知a1+2a2+22a3+…+2n-1an=9-6n,则数列{an}的通项公式是________.
【解析】令Sn=a1+2a2+22a3+…+2n-1an,则Sn=9-6n,当n=1时,a1=S1=3;
当n≥2时·an=Sn-Sn-1=-6,所以an=-.所以通项公式an=
答案:an=
【解题策略提醒】
通项与和的求法
1.由递推公式求数列通项公式时,一是要注意判别类型与方法.二是要注意an的完整表达式,易忽视n=1的情况.常用的数列通项公式的求法有:(1)定义法,即直接利用等差数列或等比数列的定义求通项的方法叫定义法,这种方法适用于已知数列类型的题目.
(2)若已知数列的前n项和Sn与an的关系,求数列{an}的通项an可用公式an=求解.
(3)对于递推公式确定的数列的求解,通常可以通过递推公式的变换,转化为等差数列或等比数列问题,有时也用到一些特殊的转化方法与特殊数列.
2.数列求和时,根据数列通项公式特征选择求和法,尤其是涉及等比数列求和时要注意公比q对Sn的影响.一般常见的求和方法有:
(1)公式法:利用等差数列或等比数列前n项和公式;
(2)分组求和法:把一个数列分成几个可以直接求和的数列;
(3)裂项相消法:有时把一个数列的通项公式分成两项差的形式,相加过程消去中间项,只剩有限项再求和;
(4)错位相减法:适用于一个等差数列和一个等比数列对应项相乘构成的数列求和;
(5)并项求和法:一个数列的前n项和中,可两两结合求解,则称之为并项求和.形如an=(-1)nf(n)类型,可采用两项合并求解.
题组训练四 等差、等比数列的判定
题11.数列{an}的前n项和为Sn,a1=1,Sn+1=4an+2(n∈N*).
(1)设bn=an+1-2an,求证:{bn}是等比数列.
(2)设cn=,求证:{cn}是等差数列.
【证明】(1)an+2=Sn+2-Sn+1=4an+1+2-4an-2=4an+1-4an.
====2.
因为S2=a1+a2=4a1+2,所以a2=5.所以b1=a2-2a1=3.所以数列{bn}是首项为3,公比为2的等比数列.
(2)由(1)知bn=3·2n-1=an+1-2an,所以=3.所以cn+1-cn=3,且c1==2,
所以数列{cn}是等差数列,公差为3,首项为2.
题12.设Sn为数列{an}的前n项和,对任意的n∈N*,都有Sn=2-an,
数列{bn}满足b1=2a1,bn=(n≥2,n∈N*).
(1)求证:数列{an}是等比数列,并求{an}的通项公式;
(2)判断数列是等差数列还是等比数列,并求数列{bn}的通项公式.
【解析】(1)当n=1时,a1=S1=2-a1,解得a1=1;
当n≥2时,an=Sn-Sn-1=an-1-an,即=(n≥2,n∈N*).
所以数列{an}是首项为1,公比为的等比数列,
故数列{an}的通项公式为an=.
(2)因为a1=1,所以b1=2a1=2.因为bn=,所以=+1,即-=1(n≥2).
所以数列是首项为,公差为1的等差数列.所以=+(n-1)·1=,
故数列{bn}的通项公式为bn=.
【解题策略提醒】
等差、等比数列的判断与证明方法
(1)定义法:an+1-an=d(常数) {an}是等差数列;=q(q为常数,q≠0) {an}是等比数列;(2)中项公式法:2an+1=an+an+2 {an}是等差数列;a=an·an+2(an≠0) {an}是等比数列;(3)通项公式法:an=kn+b(k,b是常数) {an}是等差数列;an=c·qn(c,q为非零常数) {an}是等比数列;(4)前n项和公式法:Sn=An2+Bn(A,B为常数,n∈N*) {an}是等差数列;Sn=Aqn-A(A,q为常数,且A≠0,q≠0,q≠1,n∈N*) {an}是等比数列.
提醒:①前两种方法是判定等差、等比数列的常用方法,而后两种方法常用于选择、填空题中的判定.②若要判定一个数列不是等差(比)数列,则只需判定其任意的连续三项不成等差(比)即可.
题组训练五 数列与函数
题13.若数列{an}的前n项和Sn=n2-n(n=1,2,3,…),则此数列的通项公式为__________;数列{nan}中数值最小的项是第________项.
【解析】利用an=求得an=3n-16.则nan=3n2-16n=3,
所以n=3时,nan的值最小.
答案:an=3n-16 3
题14.若数列{an}的通项公式为an=n2+λn,且{an}是递增数列,则实数λ的取值范围是________.
【解析】方法一:an+1-an=(n+1)2+λ(n+1)-(n2+λn)=2n+1+λ,
由于{an}是递增数列,故2n+1+λ>0恒成立,即λ>-2n-1,
又n∈N*,-2n-1≤-3,故λ>-3.
方法二:由于函数y=x2+λx在上单调递增,结合其图象可知,若数列{an}是递增数列,则a2>a1,即22+2λ>1+λ,即λ>-3.
答案:(-3,+∞)
题15.设数列{an},{bn}满足a1=b1=6,a2=b2=4,a3=b3=3,若{an+1-an}是等差数列,{bn+1-bn}是等比数列.
(1)分别求出数列{an},{bn}的通项公式;
(2)求数列{an}中最小项及最小项的值.
【解析】(1)a2-a1=-2,a3-a2=-1,由{an+1-an}成等差数列知其公差为1,
故an+1-an=-2+(n-1)·1=n-3;b2-b1=-2,b3-b2=-1,
由{bn+1-bn}成等比数列知,其公比为,故bn+1-bn=-2·,
an=(an-an-1)+(an-1-an-2)+(an-2-an-3)+…+(a2-a1)+a1
=(n-1)·(-2)+·1+6=-2n+8=,
bn=(bn-bn-1)+(bn-1-bn-2)+(bn-2-bn-3)+…+(b2-b1)+b1=+6=2+23-n.
(2)因为an==2+,
所以n=3或n=4时,an取到最小值,最小值为a3=a4=3.
【解题策略提醒】
函数思想在数列问题中的应用
数列可以看作是定义域为正整数集(或其有限子集{1,2,3,…,n})的特殊函数.运用函数思想去研究数列,就是要借助于函数的单调性、图象和最值等知识解决与数列相关的问题.等差数列与一次函数、等比数列与指数函数有着密切的关系,等差数列前n项和公式与二次函数有密切关系,故可用函数的思想来解决数列问题.
- 1 - / 18
