直线与圆锥曲线[上学期]
图片预览





文档简介
课件15张PPT。2006、12、05课题:直线与圆锥曲线汉寿县第三中学艾镇南概念复习:(一)直线 (A、B不同时为0)当A、B都不为0时,为二元一次方程当A或B一个为0时,为一元一次方程(二)圆锥曲线有:圆、椭圆、双曲线、抛物线圆:椭圆:双曲线:抛物线:这些都是二元二次方程 1、二元二次式,但没有 的交叉项;
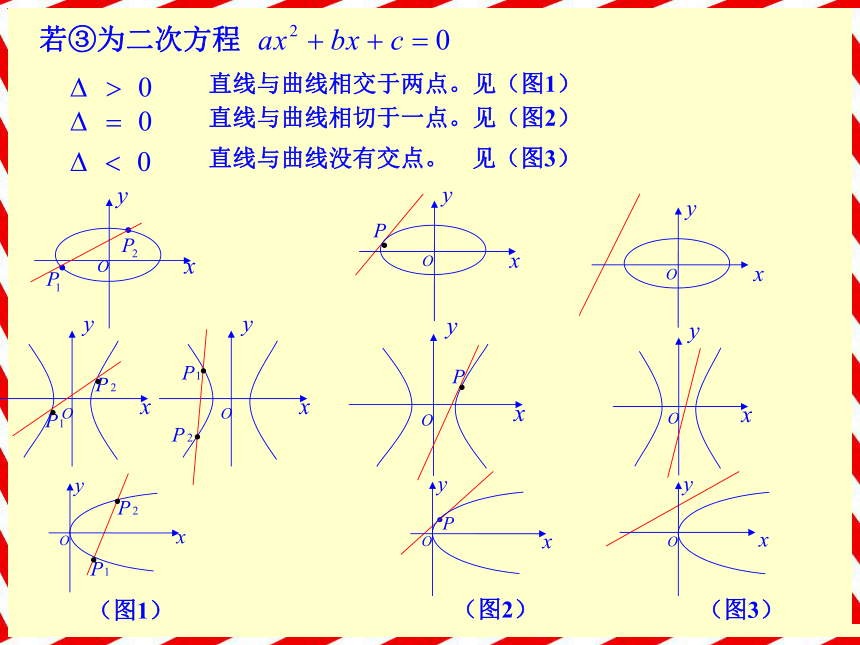
2、均可化为 的形式。 圆锥曲线方程的特点: (三)圆锥曲线与直线的交点是的解,方程组①②方程②代入方程①消元并整理得一元方程③,若方程③为一次方程,此时只有两种情况:直 线与抛 物 线 的 对 称 轴 平行直 线 与 双 曲 线 的 渐 近 线 平行此时现象是直线与曲线相交于一点若③为二次方程直线与曲线相交于两点。见(图1)直线与曲线没有交点。 见(图3)直线与曲线相切于一点。见(图2)例1 过双曲线 的左焦点 的直线与双曲线交于A、B。若|AB| = 9,问这样的直线有几条?分析:该问题是直线绕点 旋转,显然考虑弦长情况应分两类进行:① 交单支。② 交两支。先研究直线绕点 旋转,弦长|AB|的变化情况。① 交单支时:② 交两支时:如图:由双曲线的对称性,显然可知这样的直线有四条归纳:处理这类问题应先理解问题中的定量和动量;切入问题时应先考虑
是一致进行,还是分类进行;考虑“量”的取值范围应注意变化的极
端情况。先通过相关计算再根据圆锥曲线的简单几何性质来判断。例题解析:而 9∈[9/2,+∞) , 9∈[8,+∞)例2 已知直线 与曲线 恰有一个公共点,求实数 的值。分析:该问题因为参数 在变化,致使直线与曲线都在变化特别地:当 时,曲线 蜕化为 显然与直线相交于一点, 当 时,直线 化简为 , 此时,直线平行于 轴,直线与该抛物线就恰有一个交点;当 时,直线与抛物线要恰有一个交点,
那么只有相切的情形了。(看右图)归纳:该类问题应先用代数方法运用分类讨论的思想解决后,再在几何上进行验证,防止漏解。解析:联立方程组①②当 时,此方程组只有一个解当 时,①代入②并整理得:③对方程 ③:当 时,此方程组只有一个解当 时,令即:,此时,直线与抛物线相切于一点综上所述:当 时,直线与曲线只有一个公共点。已知直线 与曲线 恰有一个公共点,求实数 的值。例3 P点是抛物线 的任意一点,当P点到直线 的距离最小时,求P到该抛物线的准线的距离。分析:显然,该抛物线的准线方程为:∴只要求出点P的坐标就行先观察点P的运动与点线距离的变化情况当我们联想到点线距离公式,就有:设:只要求该函数取得最小值时的 x 就行了解法一:设:则点P到直线 的距离当且仅当 时∴此时由于 的准线方程为∴此时点P到抛物线的距离为例3 P点是抛物线 的任意一点,当P点到直线 的距离最小时,求P到该抛物线的准线的距离。当我们用直线的运动来看该问题时,就有:直线向抛物线作平移运动至两线相切时的切点P为所求。
解法二:设与直线 平行的直线方程为联立:①②②代入①得方程③对方程③,令得:此时方程③有∴此时以下解法同解法一例3 P点是抛物线 的任意一点,当P点到直线 的距离最小时,求P到该抛物线的准线的距离。归纳:这类问题的两种解决方法
(1)应用点到直线的距离公式来求解;
(2)考查与已知直线平行且与圆锥曲线相切的切线方程,再结合平行线间等距的特点完成求解。例4 求直线 被抛物线 截得的线段之长. 分析一:将直线方程与抛物线方程联立,求得直线与抛物线的交点坐标,再利用两点间的距离公式求出弦长。解法一:由解得 即直线与抛物线的交点为A(3/2,9/2)、B(-1,2),∴|AB|=∴所截线段之长为 .分析二:设直线与抛物线的交点为 ,则由|AB|= 及 、 ,得|AB|=例4 求直线 y = x + 3 被抛物线 y = 2 x 2 截得的线段之长. 解法二:设直线 与抛物线 的交点坐标为
,则由方程组 ,得 , ∴ ,又∵点A、B都在直线 y=x+3上, ∴ , ,∴|AB|= ∴所截线段之长为 .归纳:这类问题的两种解决方法
(1)联立方程组,解出直线与圆锥曲线的交点,再利用两点距离公式来求解;
(2)联立方程组,运用“设而不求”解法技巧,结合韦达定理完成求解。小结:在比较熟练掌握解有关圆锥曲线方程与直线方程联立方程组的各环节知识的同时,还需要熟练掌握解析几何中的各类公式。比如:弦长公式:定比分点公式: 等。希望同学们在扎实地掌握各种解题方法的同时,还要掌握好各种数学运算和变换的手段和技巧。点线距离公式两点距离公式2 已知一圆C的圆心为(2,-1),且该圆被直线:x-y-1=0 截得的弦长为2,求该圆的方程及过弦的两端点的切线方程。 1已知直线 ,曲线 有两个公共点,求b的取值范围。3 直线 与双曲线 的左支仅有一个公共点,求K的取值范围。巩固练习:(1≤b< )4 当抛物线y2=x上一点A到直线x-3y+4=0的距离最短时,求A的坐标及最短距离。 提高练习:再见
2、均可化为 的形式。 圆锥曲线方程的特点: (三)圆锥曲线与直线的交点是的解,方程组①②方程②代入方程①消元并整理得一元方程③,若方程③为一次方程,此时只有两种情况:直 线与抛 物 线 的 对 称 轴 平行直 线 与 双 曲 线 的 渐 近 线 平行此时现象是直线与曲线相交于一点若③为二次方程直线与曲线相交于两点。见(图1)直线与曲线没有交点。 见(图3)直线与曲线相切于一点。见(图2)例1 过双曲线 的左焦点 的直线与双曲线交于A、B。若|AB| = 9,问这样的直线有几条?分析:该问题是直线绕点 旋转,显然考虑弦长情况应分两类进行:① 交单支。② 交两支。先研究直线绕点 旋转,弦长|AB|的变化情况。① 交单支时:② 交两支时:如图:由双曲线的对称性,显然可知这样的直线有四条归纳:处理这类问题应先理解问题中的定量和动量;切入问题时应先考虑
是一致进行,还是分类进行;考虑“量”的取值范围应注意变化的极
端情况。先通过相关计算再根据圆锥曲线的简单几何性质来判断。例题解析:而 9∈[9/2,+∞) , 9∈[8,+∞)例2 已知直线 与曲线 恰有一个公共点,求实数 的值。分析:该问题因为参数 在变化,致使直线与曲线都在变化特别地:当 时,曲线 蜕化为 显然与直线相交于一点, 当 时,直线 化简为 , 此时,直线平行于 轴,直线与该抛物线就恰有一个交点;当 时,直线与抛物线要恰有一个交点,
那么只有相切的情形了。(看右图)归纳:该类问题应先用代数方法运用分类讨论的思想解决后,再在几何上进行验证,防止漏解。解析:联立方程组①②当 时,此方程组只有一个解当 时,①代入②并整理得:③对方程 ③:当 时,此方程组只有一个解当 时,令即:,此时,直线与抛物线相切于一点综上所述:当 时,直线与曲线只有一个公共点。已知直线 与曲线 恰有一个公共点,求实数 的值。例3 P点是抛物线 的任意一点,当P点到直线 的距离最小时,求P到该抛物线的准线的距离。分析:显然,该抛物线的准线方程为:∴只要求出点P的坐标就行先观察点P的运动与点线距离的变化情况当我们联想到点线距离公式,就有:设:只要求该函数取得最小值时的 x 就行了解法一:设:则点P到直线 的距离当且仅当 时∴此时由于 的准线方程为∴此时点P到抛物线的距离为例3 P点是抛物线 的任意一点,当P点到直线 的距离最小时,求P到该抛物线的准线的距离。当我们用直线的运动来看该问题时,就有:直线向抛物线作平移运动至两线相切时的切点P为所求。
解法二:设与直线 平行的直线方程为联立:①②②代入①得方程③对方程③,令得:此时方程③有∴此时以下解法同解法一例3 P点是抛物线 的任意一点,当P点到直线 的距离最小时,求P到该抛物线的准线的距离。归纳:这类问题的两种解决方法
(1)应用点到直线的距离公式来求解;
(2)考查与已知直线平行且与圆锥曲线相切的切线方程,再结合平行线间等距的特点完成求解。例4 求直线 被抛物线 截得的线段之长. 分析一:将直线方程与抛物线方程联立,求得直线与抛物线的交点坐标,再利用两点间的距离公式求出弦长。解法一:由解得 即直线与抛物线的交点为A(3/2,9/2)、B(-1,2),∴|AB|=∴所截线段之长为 .分析二:设直线与抛物线的交点为 ,则由|AB|= 及 、 ,得|AB|=例4 求直线 y = x + 3 被抛物线 y = 2 x 2 截得的线段之长. 解法二:设直线 与抛物线 的交点坐标为
,则由方程组 ,得 , ∴ ,又∵点A、B都在直线 y=x+3上, ∴ , ,∴|AB|= ∴所截线段之长为 .归纳:这类问题的两种解决方法
(1)联立方程组,解出直线与圆锥曲线的交点,再利用两点距离公式来求解;
(2)联立方程组,运用“设而不求”解法技巧,结合韦达定理完成求解。小结:在比较熟练掌握解有关圆锥曲线方程与直线方程联立方程组的各环节知识的同时,还需要熟练掌握解析几何中的各类公式。比如:弦长公式:定比分点公式: 等。希望同学们在扎实地掌握各种解题方法的同时,还要掌握好各种数学运算和变换的手段和技巧。点线距离公式两点距离公式2 已知一圆C的圆心为(2,-1),且该圆被直线:x-y-1=0 截得的弦长为2,求该圆的方程及过弦的两端点的切线方程。 1已知直线 ,曲线 有两个公共点,求b的取值范围。3 直线 与双曲线 的左支仅有一个公共点,求K的取值范围。巩固练习:(1≤b< )4 当抛物线y2=x上一点A到直线x-3y+4=0的距离最短时,求A的坐标及最短距离。 提高练习:再见
