华师大版九年级数学(上册)《第25章 解直角三角形》单元检测题(含答案详解)
文档属性
| 名称 | 华师大版九年级数学(上册)《第25章 解直角三角形》单元检测题(含答案详解) |  | |
| 格式 | zip | ||
| 文件大小 | 421.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-02-08 18:17:27 | ||
图片预览


文档简介
第25章 解直角三角形检测题
(时间:90分钟,满分:100分)
一、选择题(每小题3分,共30分)
1.计算:
A. B. C. D.
2.在△中,∠=90°,如果,,那么sin 的值是( ).
A. B. C. D.
3.在△中,∠=90,,,则sin( )
A. B. C. D.
4. 在△ABC中,若三边BC、CA、AB满足 BC∶CA∶AB=5∶12∶13,则cos B( )
A. B. C. D.
5.在△中,∠=90°,,则sin 的值是( )
A. B. C. 1 D.
6.已知在中,,则的值为( )
A. B. C. D.
7.如图,一个小球由地面沿着坡度的坡面向上前进了10 m,此时小球距离地面的高度为( )
A. B.2 m C.4 m D. m
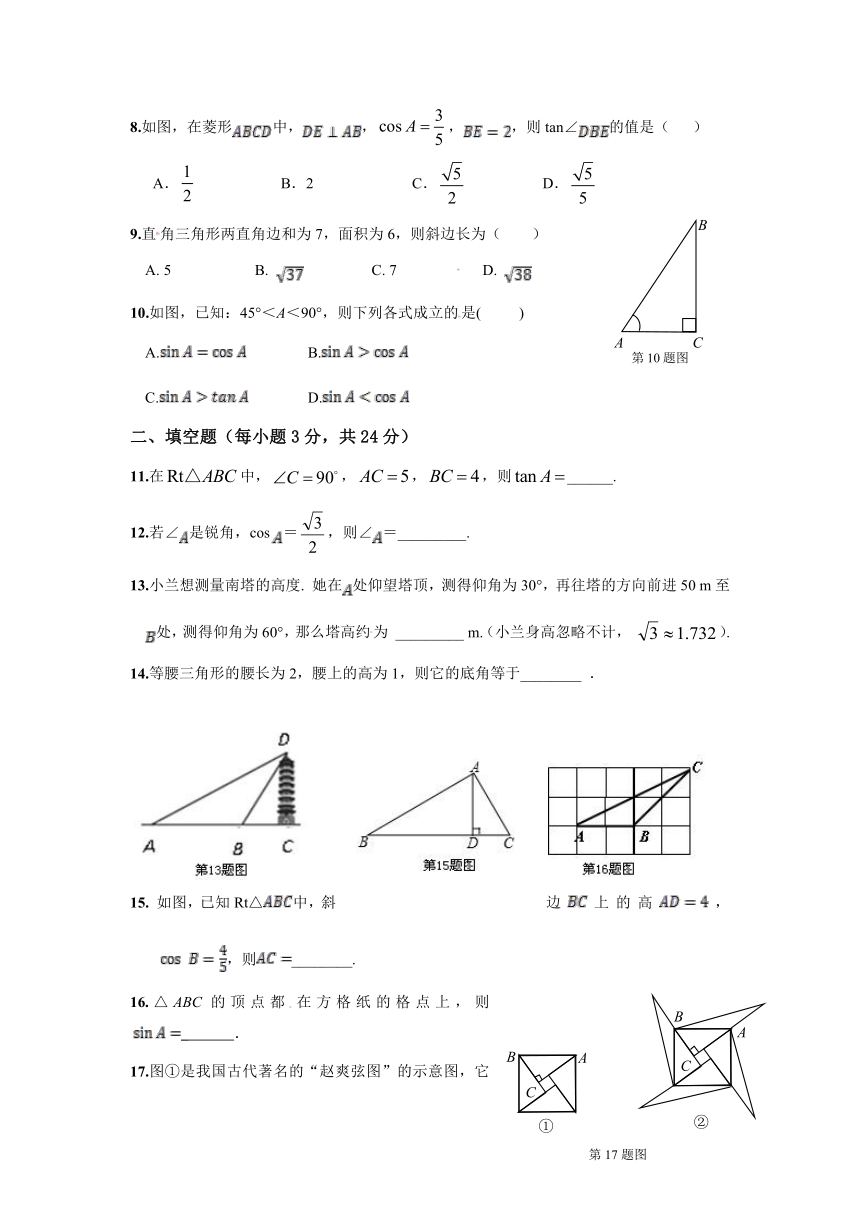
8.如图,在菱形中,,,,则tan∠的值是( )
A. B.2 C. D.
9.直角三角形两直角边和为7,面积为6,则斜边长为( )
A. 5 B. C. 7 D.
10.如图,已知:45°<A<90°,则下列各式成立的是( )
A. B.
C. D.
二、填空题(每小题3分,共24分)
11.在中,,,,则______.
12.若∠是锐角,cos=,则∠=_________.
13.小兰想测量南塔的高度. 她在处仰望塔顶,测得仰角为30°,再往塔的方向前进50 m至处,测得仰角为60°,那么塔高约为 _________ m.(小兰身高忽略不计, ).
14.等腰三角形的腰长为2,腰上的高为1,则它的底角等于________ .
15. 如图,已知Rt△中,斜边上的高,,则________.
16.△ABC的顶点都在方格纸的格点上,则_ .
17.图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图②所示的“数学风车”,则这个风车的外围周长是__________.
18.如图是一个艺术窗的一部分,所有的四边形都是正方形,三角形是直角三角形,其中最大正方形的边长为,则正方形A,B的面积和是_________.
三、解答题(共46分)
19.(8分)计算下列各题:
(1) ;(2).
20.(6分)在数学活动课上,九年级(1)班数学兴趣小组的同学们测量校园内一棵大树的高度,设计的方案及测量数据如下:
(1)在大树前的平地上选择一点,测得由点看大树顶端的仰角为35°;
(2)在点和大树之间选择一点(、、在同一直线上),测得由点看大树顶端的仰角恰好为45°;
(3)量出、两点间的距离为4.5 .
请你根据以上数据求出大树的高度.(结果保留3个有效数字)
21.(6分)每年的5月15日是“世界助残日”.某商场门前的台阶共高出地面1.2米,为帮助残疾人便于轮椅行走,准备拆除台阶换成斜坡,又考虑安全,轮椅行走斜坡的坡角不得超过,已知此商场门前的人行道距商场门的水平距离为8米(斜坡不能修在人行道上),问此商场能否把台阶换成斜坡
(参考数据:)
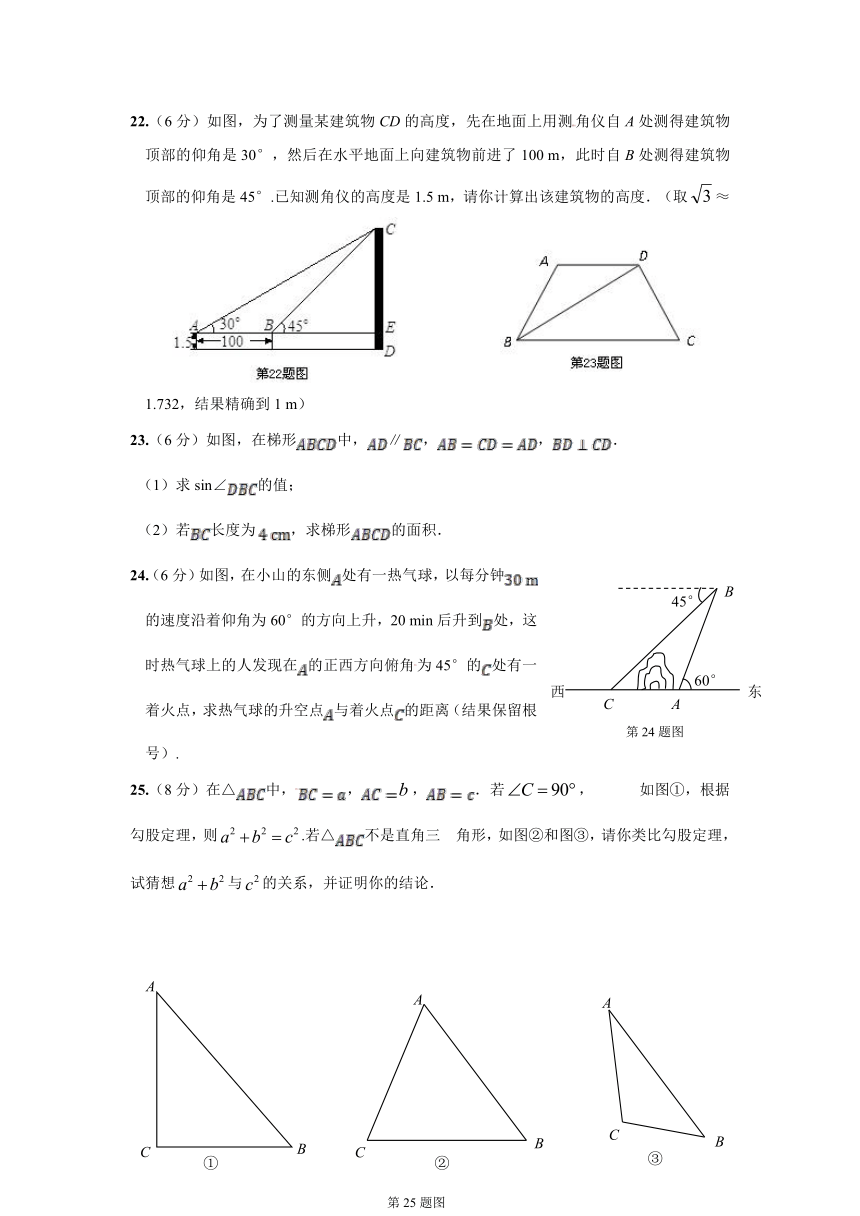
22.(6分)如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100 m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5 m,请你计算出该建筑物的高度.(取≈1.732,结果精确到1 m)
23.(6分)如图,在梯形中,∥,,.
(1)求sin∠的值;
(2)若长度为,求梯形的面积.
24.(6分)如图,在小山的东侧处有一热气球,以每分钟的速度沿着仰角为60°的方向上升,20 min后升到处,这时热气球上的人发现在的正西方向俯角为45°的处有一着火点,求热气球的升空点与着火点的距离(结果保留根号).
25.(8分)在△中,,,.若, 如图①,根据勾股定理,则.若△不是直角三 角形,如图②和图③,请你类比勾股定理,试猜想与的关系,并证明你的结论.
第25章 解直角三角形检测题参考答案
1.C 解析:.
2.A 解析:如图,
3.D 解析:由勾股定理知,所以所以sin
4.C 解析:设,则,,则,所以△是直角三角形,且∠.所以在△ABC中,.
5.B 解析:因为∠=90°,,
所以.
6.A 解析:如图,设则由勾股定理知,所以
7.B 解析:设小球距离地面的高度为则小球水平移动的距离为 所以解得
8.B 解析:设又因为在菱形中,所以所以所以由勾股定理知所以2
9.A 解析:设直角三角形的两直角边长分别为则所以斜边长
10.B 解析:在锐角三角函数中仅当45°时,,所以选项错误;因为45°<A<90°,所以B<45°,即A>B,所以BC>AC,所以>,即,所以选项正确,选项错误 >1,<1,所以选项错误..
11. 解析:如图,
12.30° 解析:因为,所以∠
13.43.3 解析:因为,所以所以所以).
14.15°或75° 解析:如图,.在图①中,,所以∠∠;在图②中,,所以∠∠.
15. 解析:在Rt△中,∵ ,∴ sin ,.
在Rt△中,∵ ,sin ,∴.
在Rt△中,∵ ,∴ .
16. 解析:利用网格,从点向所在直线作垂线,利用勾股定理得,所以.
17.76 解析:如图,因为,所以 由勾股定理得所以这个风车的外围周长为
18.25 解析:设正方形A的边长为正方形B的边长为则,所以.
19.解:(1)
(2)
20.解:∵ ∠90°, ∠45°, ∴
∵ ,∴
则 m,
∵ ∠35°,∴ tan∠tan 35° .
整理,得≈10.5.
故大树的高约为10.5
21.解:因为所以斜坡的坡角小于 ,
故此商场能把台阶换成斜坡.
22.解:设,则由题意可知,m.
在Rt△AEC中,tan∠CAE=,即tan 30°=,
∴,即3x(x+100),解得x50+50.
经检验50+50是原方程的解.
∴
故该建筑物的高度约为
23.解:(1)∵,∴ ∠∠.
∵ ∥,∴ ∠∠∠.
在梯形中,∵,∴ ∠∠∠∠
∵,∴ 3∠ ,∴ ∠30 ,∴
(2)过作于点.
在Rt△中, ∠,
∠,∴
在Rt△中,,
∴
24.解:过作于,则.
因为∠,300m,
所以300(-1)即热气球的升空点与着火点的距离为300(-1)
25.解:如图①,若△是锐角三角形,则有.证明如下:
过点作,垂足为,设为,则有.
根据勾股定理,得,即.
∴ .
∵ ,∴ ,∴ .
如图②,若△是钝角三角形,为钝角,则有. 证明如下:
过点作,交的延长线于.
设为,则有,根据勾股定理,得.
即.
∵ ,∴ ,∴ .
第7题图
A
B
C
第10题图
①1
A
B
C
②2
A
B
C
第17题图
B
A
第18题图
第20题图
B
C
A
东
西
45°
60°
第24题图
A
B
C
A
B
C
A
B
C
①
② = 1 \* GB3 ①
③ = 1 \* GB3 ①
第25题图
A
B
C
第2题答图
A
B
C
第6题答图
第11题答图
A
B
C
第14题答图
B
C
D
②
A
A
B
C
D
①
第17题答图
A
B
C
D
A
B
C
①
D①
A
B
C
② = 1 \* GB3 ①
D①
第25题答图
(时间:90分钟,满分:100分)
一、选择题(每小题3分,共30分)
1.计算:
A. B. C. D.
2.在△中,∠=90°,如果,,那么sin 的值是( ).
A. B. C. D.
3.在△中,∠=90,,,则sin( )
A. B. C. D.
4. 在△ABC中,若三边BC、CA、AB满足 BC∶CA∶AB=5∶12∶13,则cos B( )
A. B. C. D.
5.在△中,∠=90°,,则sin 的值是( )
A. B. C. 1 D.
6.已知在中,,则的值为( )
A. B. C. D.
7.如图,一个小球由地面沿着坡度的坡面向上前进了10 m,此时小球距离地面的高度为( )
A. B.2 m C.4 m D. m
8.如图,在菱形中,,,,则tan∠的值是( )
A. B.2 C. D.
9.直角三角形两直角边和为7,面积为6,则斜边长为( )
A. 5 B. C. 7 D.
10.如图,已知:45°<A<90°,则下列各式成立的是( )
A. B.
C. D.
二、填空题(每小题3分,共24分)
11.在中,,,,则______.
12.若∠是锐角,cos=,则∠=_________.
13.小兰想测量南塔的高度. 她在处仰望塔顶,测得仰角为30°,再往塔的方向前进50 m至处,测得仰角为60°,那么塔高约为 _________ m.(小兰身高忽略不计, ).
14.等腰三角形的腰长为2,腰上的高为1,则它的底角等于________ .
15. 如图,已知Rt△中,斜边上的高,,则________.
16.△ABC的顶点都在方格纸的格点上,则_ .
17.图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图②所示的“数学风车”,则这个风车的外围周长是__________.
18.如图是一个艺术窗的一部分,所有的四边形都是正方形,三角形是直角三角形,其中最大正方形的边长为,则正方形A,B的面积和是_________.
三、解答题(共46分)
19.(8分)计算下列各题:
(1) ;(2).
20.(6分)在数学活动课上,九年级(1)班数学兴趣小组的同学们测量校园内一棵大树的高度,设计的方案及测量数据如下:
(1)在大树前的平地上选择一点,测得由点看大树顶端的仰角为35°;
(2)在点和大树之间选择一点(、、在同一直线上),测得由点看大树顶端的仰角恰好为45°;
(3)量出、两点间的距离为4.5 .
请你根据以上数据求出大树的高度.(结果保留3个有效数字)
21.(6分)每年的5月15日是“世界助残日”.某商场门前的台阶共高出地面1.2米,为帮助残疾人便于轮椅行走,准备拆除台阶换成斜坡,又考虑安全,轮椅行走斜坡的坡角不得超过,已知此商场门前的人行道距商场门的水平距离为8米(斜坡不能修在人行道上),问此商场能否把台阶换成斜坡
(参考数据:)
22.(6分)如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100 m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5 m,请你计算出该建筑物的高度.(取≈1.732,结果精确到1 m)
23.(6分)如图,在梯形中,∥,,.
(1)求sin∠的值;
(2)若长度为,求梯形的面积.
24.(6分)如图,在小山的东侧处有一热气球,以每分钟的速度沿着仰角为60°的方向上升,20 min后升到处,这时热气球上的人发现在的正西方向俯角为45°的处有一着火点,求热气球的升空点与着火点的距离(结果保留根号).
25.(8分)在△中,,,.若, 如图①,根据勾股定理,则.若△不是直角三 角形,如图②和图③,请你类比勾股定理,试猜想与的关系,并证明你的结论.
第25章 解直角三角形检测题参考答案
1.C 解析:.
2.A 解析:如图,
3.D 解析:由勾股定理知,所以所以sin
4.C 解析:设,则,,则,所以△是直角三角形,且∠.所以在△ABC中,.
5.B 解析:因为∠=90°,,
所以.
6.A 解析:如图,设则由勾股定理知,所以
7.B 解析:设小球距离地面的高度为则小球水平移动的距离为 所以解得
8.B 解析:设又因为在菱形中,所以所以所以由勾股定理知所以2
9.A 解析:设直角三角形的两直角边长分别为则所以斜边长
10.B 解析:在锐角三角函数中仅当45°时,,所以选项错误;因为45°<A<90°,所以B<45°,即A>B,所以BC>AC,所以>,即,所以选项正确,选项错误 >1,<1,所以选项错误..
11. 解析:如图,
12.30° 解析:因为,所以∠
13.43.3 解析:因为,所以所以所以).
14.15°或75° 解析:如图,.在图①中,,所以∠∠;在图②中,,所以∠∠.
15. 解析:在Rt△中,∵ ,∴ sin ,.
在Rt△中,∵ ,sin ,∴.
在Rt△中,∵ ,∴ .
16. 解析:利用网格,从点向所在直线作垂线,利用勾股定理得,所以.
17.76 解析:如图,因为,所以 由勾股定理得所以这个风车的外围周长为
18.25 解析:设正方形A的边长为正方形B的边长为则,所以.
19.解:(1)
(2)
20.解:∵ ∠90°, ∠45°, ∴
∵ ,∴
则 m,
∵ ∠35°,∴ tan∠tan 35° .
整理,得≈10.5.
故大树的高约为10.5
21.解:因为所以斜坡的坡角小于 ,
故此商场能把台阶换成斜坡.
22.解:设,则由题意可知,m.
在Rt△AEC中,tan∠CAE=,即tan 30°=,
∴,即3x(x+100),解得x50+50.
经检验50+50是原方程的解.
∴
故该建筑物的高度约为
23.解:(1)∵,∴ ∠∠.
∵ ∥,∴ ∠∠∠.
在梯形中,∵,∴ ∠∠∠∠
∵,∴ 3∠ ,∴ ∠30 ,∴
(2)过作于点.
在Rt△中, ∠,
∠,∴
在Rt△中,,
∴
24.解:过作于,则.
因为∠,300m,
所以300(-1)即热气球的升空点与着火点的距离为300(-1)
25.解:如图①,若△是锐角三角形,则有.证明如下:
过点作,垂足为,设为,则有.
根据勾股定理,得,即.
∴ .
∵ ,∴ ,∴ .
如图②,若△是钝角三角形,为钝角,则有. 证明如下:
过点作,交的延长线于.
设为,则有,根据勾股定理,得.
即.
∵ ,∴ ,∴ .
第7题图
A
B
C
第10题图
①1
A
B
C
②2
A
B
C
第17题图
B
A
第18题图
第20题图
B
C
A
东
西
45°
60°
第24题图
A
B
C
A
B
C
A
B
C
①
② = 1 \* GB3 ①
③ = 1 \* GB3 ①
第25题图
A
B
C
第2题答图
A
B
C
第6题答图
第11题答图
A
B
C
第14题答图
B
C
D
②
A
A
B
C
D
①
第17题答图
A
B
C
D
A
B
C
①
D①
A
B
C
② = 1 \* GB3 ①
D①
第25题答图
