27.2.2 相似三角形应用举例(第一课时)-测量物体高度
文档属性
| 名称 | 27.2.2 相似三角形应用举例(第一课时)-测量物体高度 |  | |
| 格式 | zip | ||
| 文件大小 | 693.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-02-09 17:02:49 | ||
图片预览




文档简介
课件14张PPT。(第一课时)§27.2.2 相似三角形应用举例1.平行法:
2.定理:
①边边边:
②边角边:
③角角:
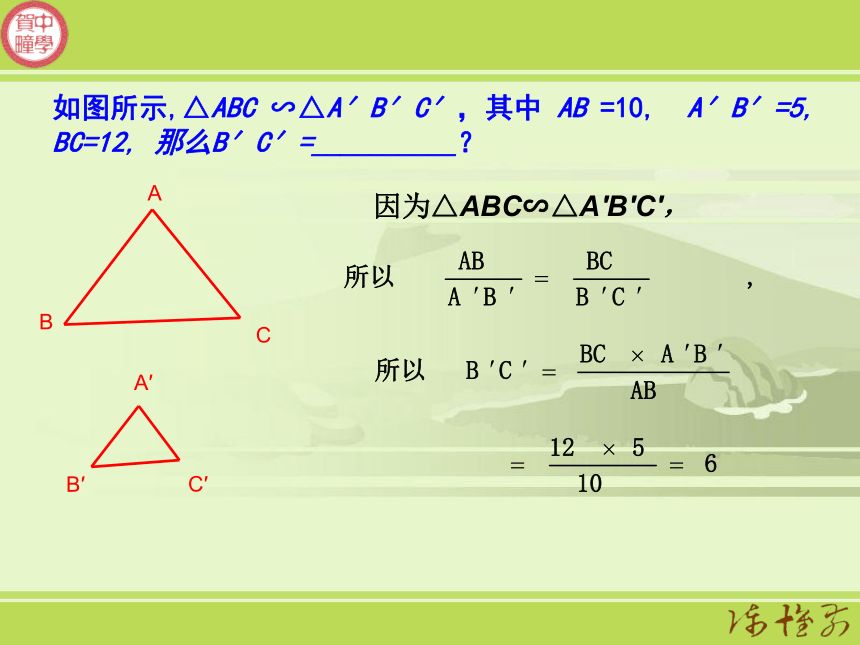
④斜边、直角边1、判断两三角形相似有哪些方法?2、相似三角形有什么性质?对应角相等,对应边的比相等如图所示,△ABC ∽△A′B′C′,其中 AB =10, A′B′=5, BC=12, 那么B′C′=__________?因为△ABC∽△A′B′C′,如何利用相似三角形的知识
解决实际实际问题?如何求旗
杆的高度?如何求河的宽?了解平行光线在阳光下,物体的高度与影长有有什么关系?同一时刻物体的
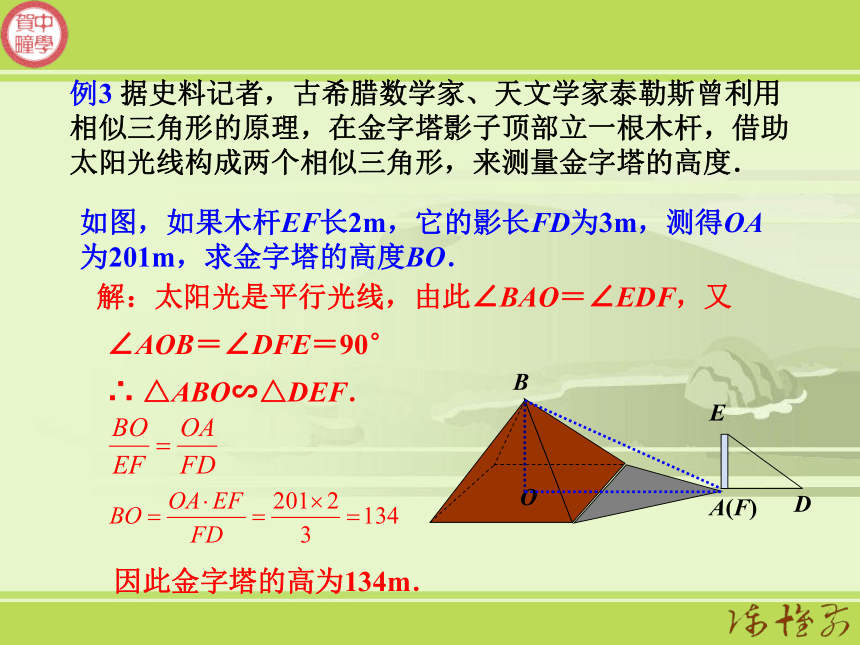
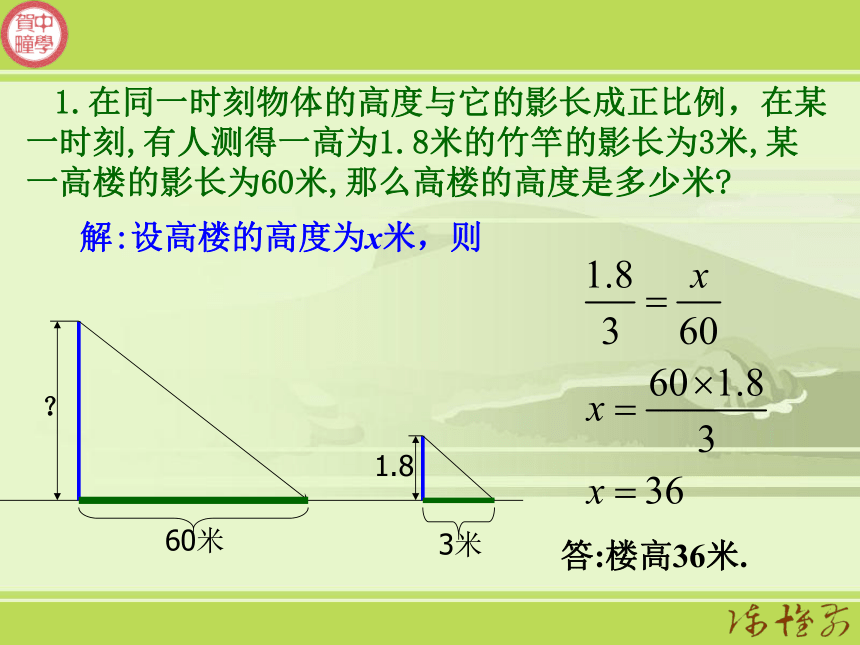
高度与影长成正比。尝试画出影子ABCDEF选择同时间测量如何运用“三角形的相似知识”来说明“平行光线的照射下,同一时刻物高与影长成比例”?例3 据史料记者,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度.如图,如果木杆EF长2m,它的影长FD为3m,测得OA为201m,求金字塔的高度BO.解:太阳光是平行光线,由此∠BAO=∠EDF,又∠AOB=∠DFE=90°∴ △ABO∽△DEF.因此金字塔的高为134m.1.在同一时刻物体的高度与它的影长成正比例,在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为60米,那么高楼的高度是多少米?解:设高楼的高度为x米,则答:楼高36米.每个星期一上午学校内的全体师生都要参加升旗仪式,想不想测量咱们旗杆的高度呢?2.小明测得旗杆的影长为12米,同一时刻把1米的标杆竖立在地上,它的影长为1.5米。于是小明很快就算出了旗杆的高度。你知道他是怎么计算的吗?121.51解:∵太阳光是平行光线∴AB=8∴ △ABC∽△DEF.∴∴(F)3.某同学想利用树影测量树高.他在某一时刻测得小树高为1.5米时,其影长为1.2米,当他测量教学楼旁的一棵大树影长时,因大树靠近教学楼,有一部分影子在墙上.经测量,地面部分影长为6.4米,墙上影长为1.4米,那么这棵大树高多少米?D6.41.2?1.51.4ABc解:作DE⊥AB于E
得
∴AE=8
∴AB=8+1.4=9.4米物体的影长不等于地上的部分加上墙上的部分为了测量校园水平地面上一棵树的高度,数学兴趣小组利用一
根标杆、皮尺,设计如图所示的测量方案.已知测量同学眼睛
A、标杆顶端F、树的顶端E在同一直线上,此同学眼睛距地面
1.6米,标杆为3.1米,且BC=1米,CD=5米,请你根据所给
出的数据求树高ED.金字塔还可以怎么测量高度?小明要测量一座古塔的高度,从距他2米的一小块积水处C看到塔顶的倒影,已知小明的眼部离地面的高度DE是1.5米,塔底中心B到积水处C的距离是40米.求塔高AB? BDCAE答:塔高30米.解:∵∠DEC=∠ABC=90° ∠DCE=∠ACB
∴△DEC∽△ABC金字塔还可以怎么测量高度?通过本节课的学习,利用相似三角形的知
识测量物体的高度有哪些方法?利用阳光下的影长测物体的高度方法一:利用标杆测物体的高度方法二:利用镜子的反射测物体的高度方法三:《名校课堂》
P39~40
知识点1
课后作业
9、11、15
2.定理:
①边边边:
②边角边:
③角角:
④斜边、直角边1、判断两三角形相似有哪些方法?2、相似三角形有什么性质?对应角相等,对应边的比相等如图所示,△ABC ∽△A′B′C′,其中 AB =10, A′B′=5, BC=12, 那么B′C′=__________?因为△ABC∽△A′B′C′,如何利用相似三角形的知识
解决实际实际问题?如何求旗
杆的高度?如何求河的宽?了解平行光线在阳光下,物体的高度与影长有有什么关系?同一时刻物体的
高度与影长成正比。尝试画出影子ABCDEF选择同时间测量如何运用“三角形的相似知识”来说明“平行光线的照射下,同一时刻物高与影长成比例”?例3 据史料记者,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度.如图,如果木杆EF长2m,它的影长FD为3m,测得OA为201m,求金字塔的高度BO.解:太阳光是平行光线,由此∠BAO=∠EDF,又∠AOB=∠DFE=90°∴ △ABO∽△DEF.因此金字塔的高为134m.1.在同一时刻物体的高度与它的影长成正比例,在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为60米,那么高楼的高度是多少米?解:设高楼的高度为x米,则答:楼高36米.每个星期一上午学校内的全体师生都要参加升旗仪式,想不想测量咱们旗杆的高度呢?2.小明测得旗杆的影长为12米,同一时刻把1米的标杆竖立在地上,它的影长为1.5米。于是小明很快就算出了旗杆的高度。你知道他是怎么计算的吗?121.51解:∵太阳光是平行光线∴AB=8∴ △ABC∽△DEF.∴∴(F)3.某同学想利用树影测量树高.他在某一时刻测得小树高为1.5米时,其影长为1.2米,当他测量教学楼旁的一棵大树影长时,因大树靠近教学楼,有一部分影子在墙上.经测量,地面部分影长为6.4米,墙上影长为1.4米,那么这棵大树高多少米?D6.41.2?1.51.4ABc解:作DE⊥AB于E
得
∴AE=8
∴AB=8+1.4=9.4米物体的影长不等于地上的部分加上墙上的部分为了测量校园水平地面上一棵树的高度,数学兴趣小组利用一
根标杆、皮尺,设计如图所示的测量方案.已知测量同学眼睛
A、标杆顶端F、树的顶端E在同一直线上,此同学眼睛距地面
1.6米,标杆为3.1米,且BC=1米,CD=5米,请你根据所给
出的数据求树高ED.金字塔还可以怎么测量高度?小明要测量一座古塔的高度,从距他2米的一小块积水处C看到塔顶的倒影,已知小明的眼部离地面的高度DE是1.5米,塔底中心B到积水处C的距离是40米.求塔高AB? BDCAE答:塔高30米.解:∵∠DEC=∠ABC=90° ∠DCE=∠ACB
∴△DEC∽△ABC金字塔还可以怎么测量高度?通过本节课的学习,利用相似三角形的知
识测量物体的高度有哪些方法?利用阳光下的影长测物体的高度方法一:利用标杆测物体的高度方法二:利用镜子的反射测物体的高度方法三:《名校课堂》
P39~40
知识点1
课后作业
9、11、15
