圆锥曲线复习[上学期]

课件24张PPT。圆锥曲线复习复习一——几何性质
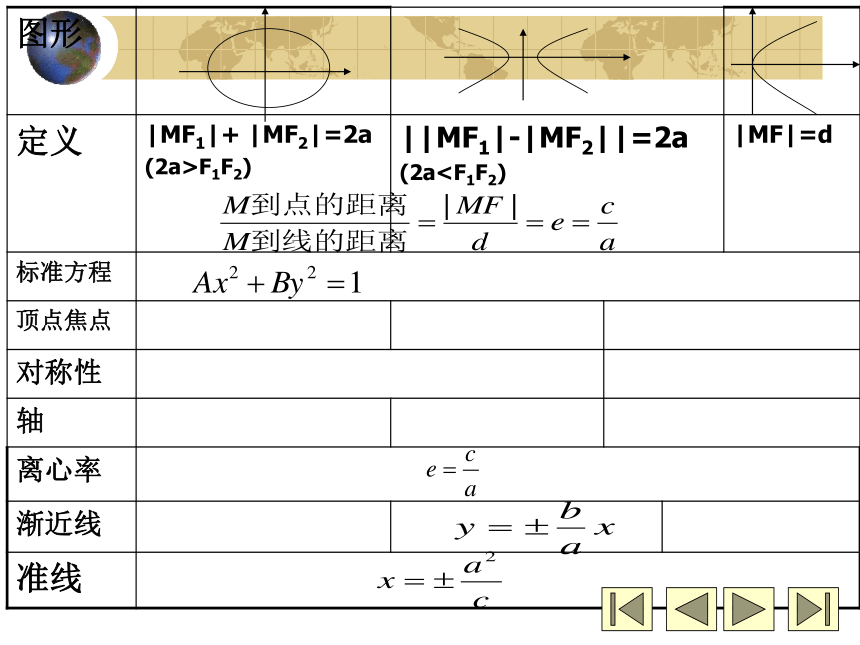
复习二——标准方程
复习三——综合圆锥圆锥曲线几何性质简单应用例题1：
例题2：
例题3：例题4：
例题5：
例题6：
例题7：练习1：小测2、椭圆 和 的关系是()
A．有相同的长、短轴 B．有相同的离心率
C．有相同的准线 D．有相同的焦点

3设F1和F2为双曲线 的两个焦点，点P在双曲线上，
且满足 ，则 =_______。
待定系数法求圆锥曲线方程例题1:
例题2：
例题3：求实半轴长等于 ，并且经过点 的双曲线的标准方程例题4：
例题5：
例题6：作业：小测1、椭圆长轴长是短轴长的2倍，焦距是 ，则它的标准方程是________ 2、双曲线的渐近方程是 ，且过点M（2，3），其标准方程为________ 3、以椭圆 的中心为顶点，椭圆的下焦点为焦点的抛物线方程为 . 定义法求轨迹方程例题1:
例题2：
例题3：已知 的周长是16， B 求动点C的轨迹方程设 的顶点 ， ，且 ，求第三个顶点C的轨迹方程 动点M到定点F（2，0）的距离比它到定直线x+5=0的
距离小3，求点M的轨迹是方程例题4：
例题5：
例题6：动圆M与 ，
求圆心M的轨迹方程 动圆M与 ，
求圆心M的轨迹方程 动圆M过点F(0，2)且与直线y=-2相切，
求圆心M的轨迹方程 小测1、 已知两点A(0 , －3)与B(0 , 3 )，若|PA|＋|PB|=10,那么P点的轨迹方程是 。
2、已知动点P到A(－5, 0)的距离与它到B(5, 0)的距离
的差等于6，则P的轨迹方程为_______.3、到椭圆 右焦点的距离与到直线

的距离相等的轨迹方程是_______.
相关点法求轨迹方程例题1:
例题2：
已知点 ，直线 ，点B是l上的动点，若过B垂直于
y轴的直线与BF的垂直平分线交于点M，求M点的轨迹方
程 例题3：例题4:抛物线x2=4y的焦点为F，过点(0，－1)作直线L交抛物线A、B两点，再以AF、BF为邻边作平行四边形FARB，试求动点R的轨迹方程 x2=4(y+3)( ) 小测直线与圆锥曲线——弦长问题例1
已知椭圆4x2+y2=1及直线y=x+m
（1）当直线和椭圆有公共点时，求m的范围
（2）求被椭圆截得的最长弦所在的直线方程
例2：直线与圆锥曲线——点差法例3：小测2．求抛物线 截直线 所得的弦长。1、直线x-y-m=0与椭圆 1有且只有一个公共点，
则m的值是（ ）
A 10 B C D
3、椭圆 中过P（1，1）的弦被点P平分，
求此弦所在直线的方程。例4例5小测2、过椭圆 内一点M（2，1）引一条弦，
使弦被M平分，求这条弦所在的直线方程。