北师大版五年级下册数学 数学好玩2 有趣的折叠 教案
文档属性
| 名称 | 北师大版五年级下册数学 数学好玩2 有趣的折叠 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 162.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-29 20:16:08 | ||
图片预览


文档简介
《有趣的折叠》教学设计
教学目标:
1、经历想一想、折一折、说一说的过程,体会立体图形和它的平面展开图之间的关系,发展空间观念。
2、能正确判断平面展开图所对应的简单立体图形。
3、在解决实际问题的过程中,使学生感受到数学与生活的紧密联系,培养学生的数学兴趣。
重点难点:
重点:能正确判断平面展开图所对应的简单立体图形。
难点:在想一想、折一折、说一说的自主学习过程中,发展空间想象的能力。
教学准备:平面展开图,PPT等
教学过程:
1、 谈话导入,开门见山
师:同学们,你们会折纸吗?你们都会折哪些东西呢?
师:看来,大家折纸的本领还真不小。今天,老师给大家带来了一些折纸作品,让咱们一起欣赏欣赏吧!(欣赏完)有什么感受?
其实,折纸不仅是一门艺术,而且还包含着不少的数学奥秘呢,大家想研究研究吗?
师:那就让咱们一起来学习《有趣的折叠》。(板书课题:有趣的折叠)
2、 从形到点,想象入微
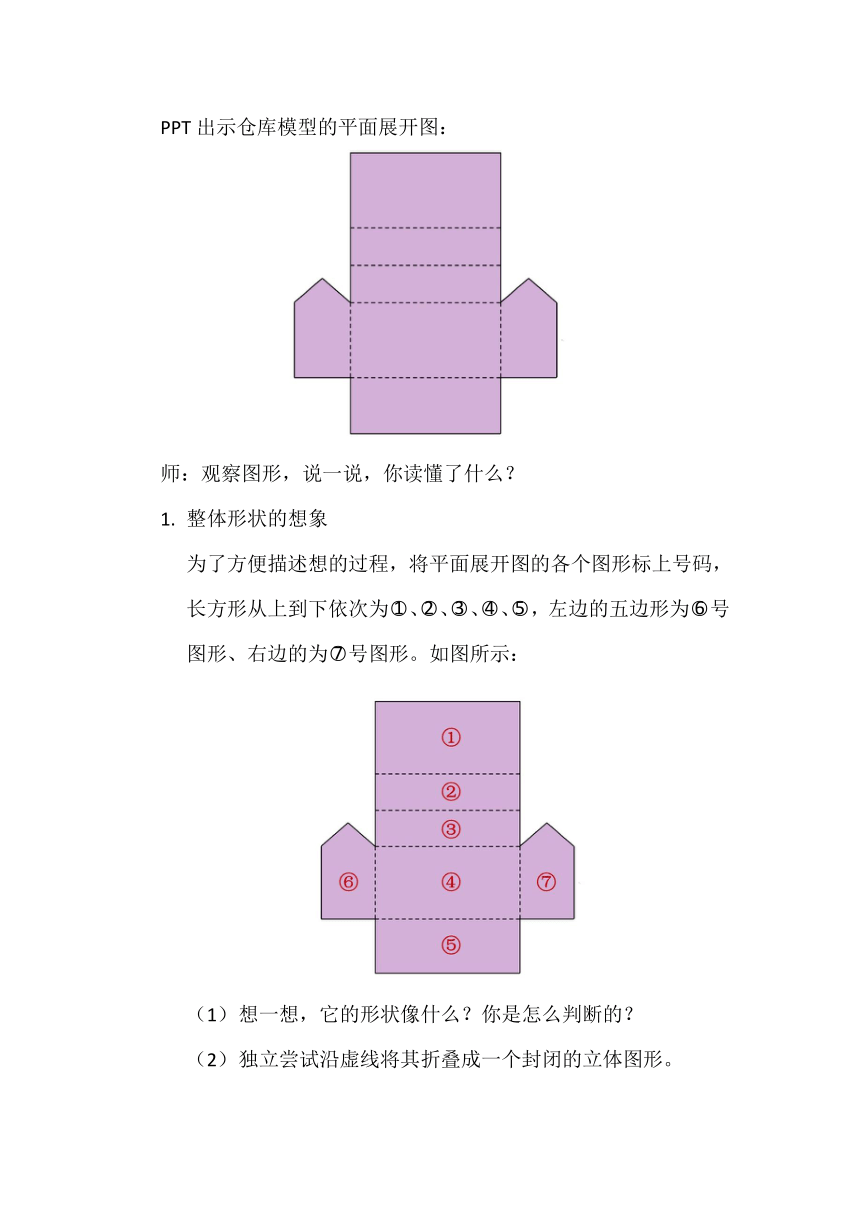
PPT出示仓库模型的平面展开图:
师:观察图形,说一说,你读懂了什么?
1. 整体形状的想象
为了方便描述想的过程,将平面展开图的各个图形标上号码,长方形从上到下依次为、、、、,左边的五边形为号图形、右边的为号图形。如图所示:
(1) 想一想,它的形状像什么?你是怎么判断的?
(2) 独立尝试沿虚线将其折叠成一个封闭的立体图形。
(3) 小组内交流,说一说自己是如何进行折叠的。
(4) 全班交流,说一说折叠的立体图形是什么,与自己想象的图形是否一致。
2. 面的想象
(1) 折叠后,与图形相对的图形是哪个图形?
(2) 折叠后,与图形相对的图形是哪个图形?
(3) 折叠后,图形是仓库的哪个部位?图形、图形呢?
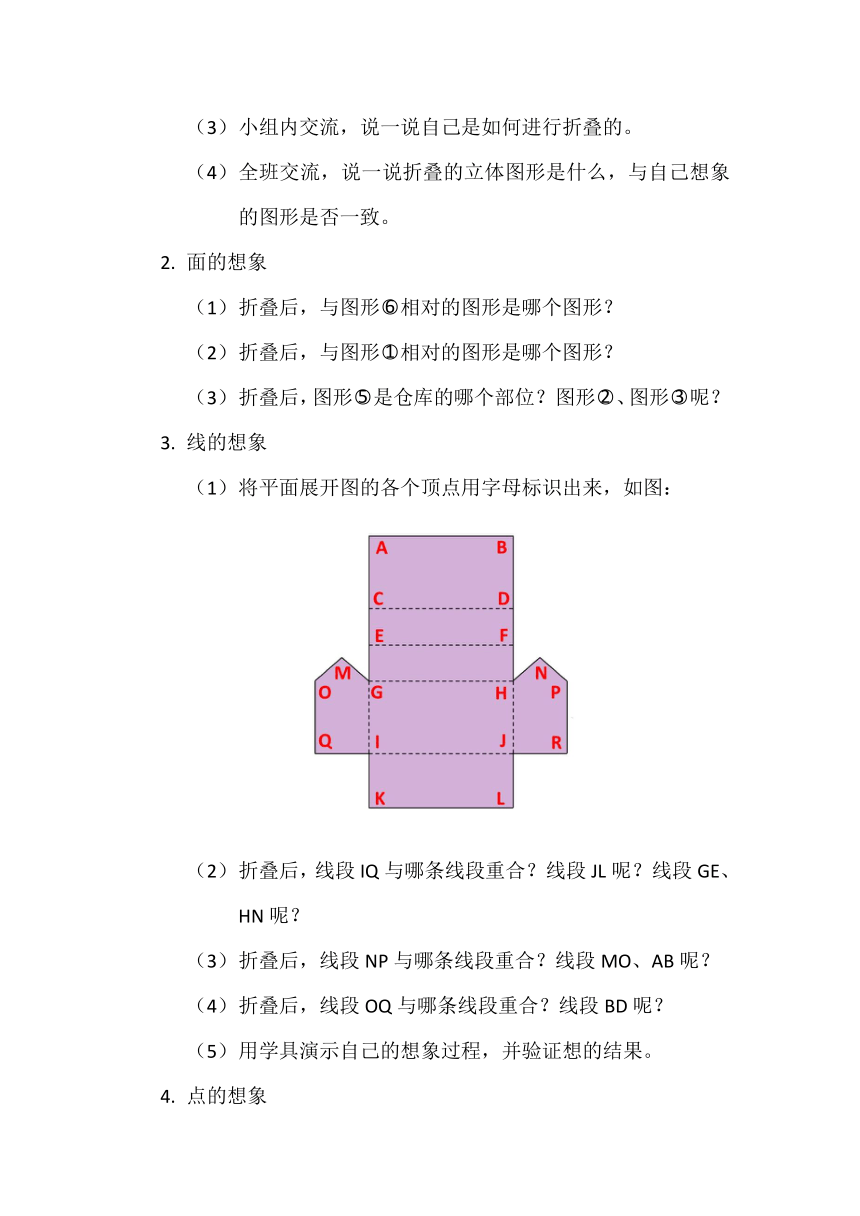
3. 线的想象
(1) 将平面展开图的各个顶点用字母标识出来,如图:
(2) 折叠后,线段IQ与哪条线段重合?线段JL呢?线段GE、HN呢?
(3) 折叠后,线段NP与哪条线段重合?线段MO、AB呢?
(4) 折叠后,线段OQ与哪条线段重合?线段BD呢?
(5) 用学具演示自己的想象过程,并验证想的结果。
4. 点的想象
(1) 折叠后,点C会与哪个点重合?点K呢?点P呢?
(2) 想一想,并在小组内交流还有哪些点会重合?
(3) 用学具演示自己的想象过程,并验证想的结果。
5. 小结
(1) 回忆一下,刚才我们经历了怎样的想象过程?
整体形状 → 面 → 线 → 点
(2) 面的想象是如何在脑海里形成的?
6. 刚才折叠出来的房子是一座仓库的模型,它各边的实际长度是图中相应长度的100倍,你知道这座仓库的占地面积是多少平方米吗?(单位:CM)
(1) 求仓库的占地面积实际上就是求仓库哪个面的面积?
(2) 仓库实际的长和宽各是多少呢?你是怎么想的?
(3) 独立计算仓库的占地面积,并在小组内交流。
(4) 全班交流,汇报结论。
3、 分级训练,发展想象
1. PPT出示教材79页问题2:下面两个展开图折叠后所围成的图形分别是什么图形?
(1) 想象这两个图形折叠后是什么形状的?能描述一下吗?
(2) 你是怎么想的?学具演示想的过程。
(3) 出示立体图形选项,连一连。
2. PPT出示教材79页问题3:下列图形中,哪个能够折叠成正方体?
(1) 说一说,哪个能够折叠成正方体?
(2) 说一说,你是如何判断的?
(3) 把能折叠成正方体的相对的面标识出来。
(4) 把各个顶点用字母标示出来,说一说折叠之后线段发生什么变化了?点呢?(以第一个图为例)
3. 小组内交流,有困难的同学可以借助学具验证。
4. PPT出示教材78页问题3的情境图。
(1) 想象平面展开图是什么样子的?
(2) 标出窗户、烟囱和小鸟的大致位置。
(3) 说一说,你是如何确定的?
4、 课堂总结,体会收获
1. 说一说,通过这节课的学习,你最大的收获是什么?
2. 你还有什么疑问吗?
板书设计:
有趣的折叠
整体形状 → 面 → 线 → 点
长:8×100 = 800(cm)
宽:3×100 = 300(cm)
800cm = 8m 300cm = 3m
8×3 = 24(m2)
设计思路:
《有趣的折叠》是北师大版五年级数学下册数学好玩中的内容,属于综合与实践教学,从发展学生数学核心素养来看,主要关注的是空间观念。在之前,学生已经学习了《展开与折叠》(长、正方体的展开图),对立体图形(这里主要指长方体和正方体)与它的平面展开图之间的关系有着初步的体验和认识。《有趣的折叠》可以看成是《展开与折叠》的延伸,将展开与折叠的立体图形对象从长方体与正方体延伸到了“不规则”(非长方体和正方体)的立体图形中,从而进一步的发展学生的空间观念。
如何进一步的发展学生的空间观念?如何知道学生是否形成了初步的空间想象方法和能力?这是我首先思考到的两个问题。要弄清楚这两个问题,还是从自己的常规教学和学生情况说起。在日常的常规教学中,受限于各种因素,我对学生空间与图形知识板块的教学重说教,轻实践,学生到底有怎样的空间想象方法和能力,可以说不容乐观的。再者,空间观念中有一个很关键的过程——“想”的过程。想,是存在于自己脑海里的东西,往往不是模糊不清就是抽象而难于言表的,老师很难从学生的答案中了解到具体的过程。据我了解,学生面对涉及空间想象类问题时,不少学生的结果往往是借助模糊的想后加以猜测得到的。怎样让想的过程更清晰一些?怎样让想象的方法更具体一些,从而促进学生空间观念的发展?通过思考,实践,我设计了如上的教学设计。
开篇导入,我借助了折纸这门艺术的欣赏,旨在拉近数学与生活、艺术的距离,激发学生的学习数学的热情和兴趣。
“从形到点,想象入微”是本节课的核心内容。为了让想的过程越来越清晰,想的事物越来越具体,我设计了这样的想的过程:整体形状 → 面 → 线 → 点,从宏观的形状轮廓逐步细微到具体的每一个点。每一个方面想的过程也不应该是简单的重复:整体形状的想象,先初步判断形状,再借助学具完成折叠过程,验证猜想,侧重于根据各种折叠的过程描述想象的过程,把具体的折叠过程转化成脑海里想的过程和方法,并强调语言表征;面的想象,是在前面实践和想象的基础上进行的,意在尝试丢掉学具,完全只通过想来完成这个过程;线和点的想象,是进一步地强化想的过程和方法,由于涉及到具体的线段和点了,学生容易想的模糊不清,这时候就需要适当地借助学具来辅助大家完成想象的过程。完成整个想象的过程后,在小结中,我提出了两个问题:(1)回忆一下,刚才我们经历了怎样的想象过程?(2)面的想象是如何在脑海里形成的?问题(1)意在引导学生总结回忆想的过程,这也包含了从整体到个体的有序思考思想,问题(2)意在让学生总结想的方法。主要问题解决了,接下来的实践应用就迎刃而解了!
“分级训练,发展想象”是对新授知识的强化巩固,基本的思路与前面相同。复杂问题强调借助学具辅助想象,清晰想象的过程。
最后的课堂总结,让学生“谈谈最大的收获是什么”是希望通过学生反馈了解学生的学习收获层次和他们的课堂感受;“你还有什么疑问吗?”,这节课中值得思考和琢磨的地方还很多,我希望我的学生们可以从中发现问题,做一个善于思考的人!
教学目标:
1、经历想一想、折一折、说一说的过程,体会立体图形和它的平面展开图之间的关系,发展空间观念。
2、能正确判断平面展开图所对应的简单立体图形。
3、在解决实际问题的过程中,使学生感受到数学与生活的紧密联系,培养学生的数学兴趣。
重点难点:
重点:能正确判断平面展开图所对应的简单立体图形。
难点:在想一想、折一折、说一说的自主学习过程中,发展空间想象的能力。
教学准备:平面展开图,PPT等
教学过程:
1、 谈话导入,开门见山
师:同学们,你们会折纸吗?你们都会折哪些东西呢?
师:看来,大家折纸的本领还真不小。今天,老师给大家带来了一些折纸作品,让咱们一起欣赏欣赏吧!(欣赏完)有什么感受?
其实,折纸不仅是一门艺术,而且还包含着不少的数学奥秘呢,大家想研究研究吗?
师:那就让咱们一起来学习《有趣的折叠》。(板书课题:有趣的折叠)
2、 从形到点,想象入微
PPT出示仓库模型的平面展开图:
师:观察图形,说一说,你读懂了什么?
1. 整体形状的想象
为了方便描述想的过程,将平面展开图的各个图形标上号码,长方形从上到下依次为、、、、,左边的五边形为号图形、右边的为号图形。如图所示:
(1) 想一想,它的形状像什么?你是怎么判断的?
(2) 独立尝试沿虚线将其折叠成一个封闭的立体图形。
(3) 小组内交流,说一说自己是如何进行折叠的。
(4) 全班交流,说一说折叠的立体图形是什么,与自己想象的图形是否一致。
2. 面的想象
(1) 折叠后,与图形相对的图形是哪个图形?
(2) 折叠后,与图形相对的图形是哪个图形?
(3) 折叠后,图形是仓库的哪个部位?图形、图形呢?
3. 线的想象
(1) 将平面展开图的各个顶点用字母标识出来,如图:
(2) 折叠后,线段IQ与哪条线段重合?线段JL呢?线段GE、HN呢?
(3) 折叠后,线段NP与哪条线段重合?线段MO、AB呢?
(4) 折叠后,线段OQ与哪条线段重合?线段BD呢?
(5) 用学具演示自己的想象过程,并验证想的结果。
4. 点的想象
(1) 折叠后,点C会与哪个点重合?点K呢?点P呢?
(2) 想一想,并在小组内交流还有哪些点会重合?
(3) 用学具演示自己的想象过程,并验证想的结果。
5. 小结
(1) 回忆一下,刚才我们经历了怎样的想象过程?
整体形状 → 面 → 线 → 点
(2) 面的想象是如何在脑海里形成的?
6. 刚才折叠出来的房子是一座仓库的模型,它各边的实际长度是图中相应长度的100倍,你知道这座仓库的占地面积是多少平方米吗?(单位:CM)
(1) 求仓库的占地面积实际上就是求仓库哪个面的面积?
(2) 仓库实际的长和宽各是多少呢?你是怎么想的?
(3) 独立计算仓库的占地面积,并在小组内交流。
(4) 全班交流,汇报结论。
3、 分级训练,发展想象
1. PPT出示教材79页问题2:下面两个展开图折叠后所围成的图形分别是什么图形?
(1) 想象这两个图形折叠后是什么形状的?能描述一下吗?
(2) 你是怎么想的?学具演示想的过程。
(3) 出示立体图形选项,连一连。
2. PPT出示教材79页问题3:下列图形中,哪个能够折叠成正方体?
(1) 说一说,哪个能够折叠成正方体?
(2) 说一说,你是如何判断的?
(3) 把能折叠成正方体的相对的面标识出来。
(4) 把各个顶点用字母标示出来,说一说折叠之后线段发生什么变化了?点呢?(以第一个图为例)
3. 小组内交流,有困难的同学可以借助学具验证。
4. PPT出示教材78页问题3的情境图。
(1) 想象平面展开图是什么样子的?
(2) 标出窗户、烟囱和小鸟的大致位置。
(3) 说一说,你是如何确定的?
4、 课堂总结,体会收获
1. 说一说,通过这节课的学习,你最大的收获是什么?
2. 你还有什么疑问吗?
板书设计:
有趣的折叠
整体形状 → 面 → 线 → 点
长:8×100 = 800(cm)
宽:3×100 = 300(cm)
800cm = 8m 300cm = 3m
8×3 = 24(m2)
设计思路:
《有趣的折叠》是北师大版五年级数学下册数学好玩中的内容,属于综合与实践教学,从发展学生数学核心素养来看,主要关注的是空间观念。在之前,学生已经学习了《展开与折叠》(长、正方体的展开图),对立体图形(这里主要指长方体和正方体)与它的平面展开图之间的关系有着初步的体验和认识。《有趣的折叠》可以看成是《展开与折叠》的延伸,将展开与折叠的立体图形对象从长方体与正方体延伸到了“不规则”(非长方体和正方体)的立体图形中,从而进一步的发展学生的空间观念。
如何进一步的发展学生的空间观念?如何知道学生是否形成了初步的空间想象方法和能力?这是我首先思考到的两个问题。要弄清楚这两个问题,还是从自己的常规教学和学生情况说起。在日常的常规教学中,受限于各种因素,我对学生空间与图形知识板块的教学重说教,轻实践,学生到底有怎样的空间想象方法和能力,可以说不容乐观的。再者,空间观念中有一个很关键的过程——“想”的过程。想,是存在于自己脑海里的东西,往往不是模糊不清就是抽象而难于言表的,老师很难从学生的答案中了解到具体的过程。据我了解,学生面对涉及空间想象类问题时,不少学生的结果往往是借助模糊的想后加以猜测得到的。怎样让想的过程更清晰一些?怎样让想象的方法更具体一些,从而促进学生空间观念的发展?通过思考,实践,我设计了如上的教学设计。
开篇导入,我借助了折纸这门艺术的欣赏,旨在拉近数学与生活、艺术的距离,激发学生的学习数学的热情和兴趣。
“从形到点,想象入微”是本节课的核心内容。为了让想的过程越来越清晰,想的事物越来越具体,我设计了这样的想的过程:整体形状 → 面 → 线 → 点,从宏观的形状轮廓逐步细微到具体的每一个点。每一个方面想的过程也不应该是简单的重复:整体形状的想象,先初步判断形状,再借助学具完成折叠过程,验证猜想,侧重于根据各种折叠的过程描述想象的过程,把具体的折叠过程转化成脑海里想的过程和方法,并强调语言表征;面的想象,是在前面实践和想象的基础上进行的,意在尝试丢掉学具,完全只通过想来完成这个过程;线和点的想象,是进一步地强化想的过程和方法,由于涉及到具体的线段和点了,学生容易想的模糊不清,这时候就需要适当地借助学具来辅助大家完成想象的过程。完成整个想象的过程后,在小结中,我提出了两个问题:(1)回忆一下,刚才我们经历了怎样的想象过程?(2)面的想象是如何在脑海里形成的?问题(1)意在引导学生总结回忆想的过程,这也包含了从整体到个体的有序思考思想,问题(2)意在让学生总结想的方法。主要问题解决了,接下来的实践应用就迎刃而解了!
“分级训练,发展想象”是对新授知识的强化巩固,基本的思路与前面相同。复杂问题强调借助学具辅助想象,清晰想象的过程。
最后的课堂总结,让学生“谈谈最大的收获是什么”是希望通过学生反馈了解学生的学习收获层次和他们的课堂感受;“你还有什么疑问吗?”,这节课中值得思考和琢磨的地方还很多,我希望我的学生们可以从中发现问题,做一个善于思考的人!
