苏教版(2019)高中数学选择性必修第一册 《5.3.1单调性》学案 (含答案)
文档属性
| 名称 | 苏教版(2019)高中数学选择性必修第一册 《5.3.1单调性》学案 (含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 527.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 11:24:40 | ||
图片预览




文档简介
§5.3.1 导数在研究函数中的应用—单调性
目标要求
1、通过实例分析,了解函数的单调性与导数的关系.
2、能利用导数判断函数的单调性、求函数的单调区间.
3、能利用导数研究函数单调性相关的问题.
学科素养目标
通过具体背景与实例的抽象,经历导数模型的建构和利用导数解决实际问题的过程,使学生对变量数学的思想方法(无穷小算法数学)有新的感悟.进一步发展学生的数学思维能力,感受和体会数学产生和发展的规律以及人类智慧和文明的传承,促进学生全面认识数学的价值.也为后继进一步学习微积分等课程打好基础.
导数与函数、方程、不等式及解析几何等相关内容密切相联.具有“集成”的特点,进而,学习本章节有助于学生从整体上理解和把握数学的结构,灵活运用数学的思想和方法,提高分析问题、解决问题的能力.
重点难点
重点:利用导数判断函数的单调性、求函数的单调区间;
难点:能利用导数研究函数单调性相关的问题.
教学过程
基础知识积累
1. 函数f(x)的单调性与导函数f′(x)正负之间的关系
在某个区间(a,b)上的函数y=f(x):
f′(x)的正负 f(x)的单调性
f′(x)>0 函数f(x)在(a,b)上___________
f′(x)<0 函数f(x)在(a,b)上___________
【课前预习思考】
(1)如果在某个区间内恒有f′(x)=0,那么函数f(x)有什么特性?
(2)在区间(a,b)内,f′(x)>0是f(x)在(a,b)上为单调增函数的什么条件?
(3)若函数f(x)为可导函数,且在区间(a,b)上是单调递增(或递减)函数,则f′(x)满足什么条件?
2.函数图象的变化趋势与导数值大小的关系
一个函数f在某一范围内导数的绝对值为,则
函数值的变化 函数的图象
越大 在这一范围内变化得较快 比较“陡峭”(向上或向下)
越小 在这一范围内变化得较慢 比较“平缓”
【课前预习思考】
某一范围内函数图象比较陡峭,是否导数值就较大?
【课前小题演练】
题1.(多选)下列命题正确的是 ( ).
A.函数f(x)在区间(a,b)上都有f′(x)<0,则函数f(x)在这个区间上单调递减.
B.函数在某一点的导数越大,函数在该点处的切线越“陡峭”.
C.函数在某个区间上变化越快,函数在这个区间上导数的绝对值越大.
D.判断函数单调性时,在区间内的个别点f′(x)=0,不影响函数在此区间的单调性.
题2.函数f(x)=ex-x的单调递增区间为__________.
题3.求函数y=x2-4x+a的单调区间.
【课堂题组训练】
类型一 导数与函数图象的关系(数学抽象、数学直观)
题4.函数y=f(x)的图象如图所示,则 ( )
A.f′(3)>0 B.f′(3)<0 C.f′(3)=0 D.f′(3)的正负不确定
题5.函数y=f(x)的图象如图所示,则导函数y=f′(x)的图象可能是 ( )
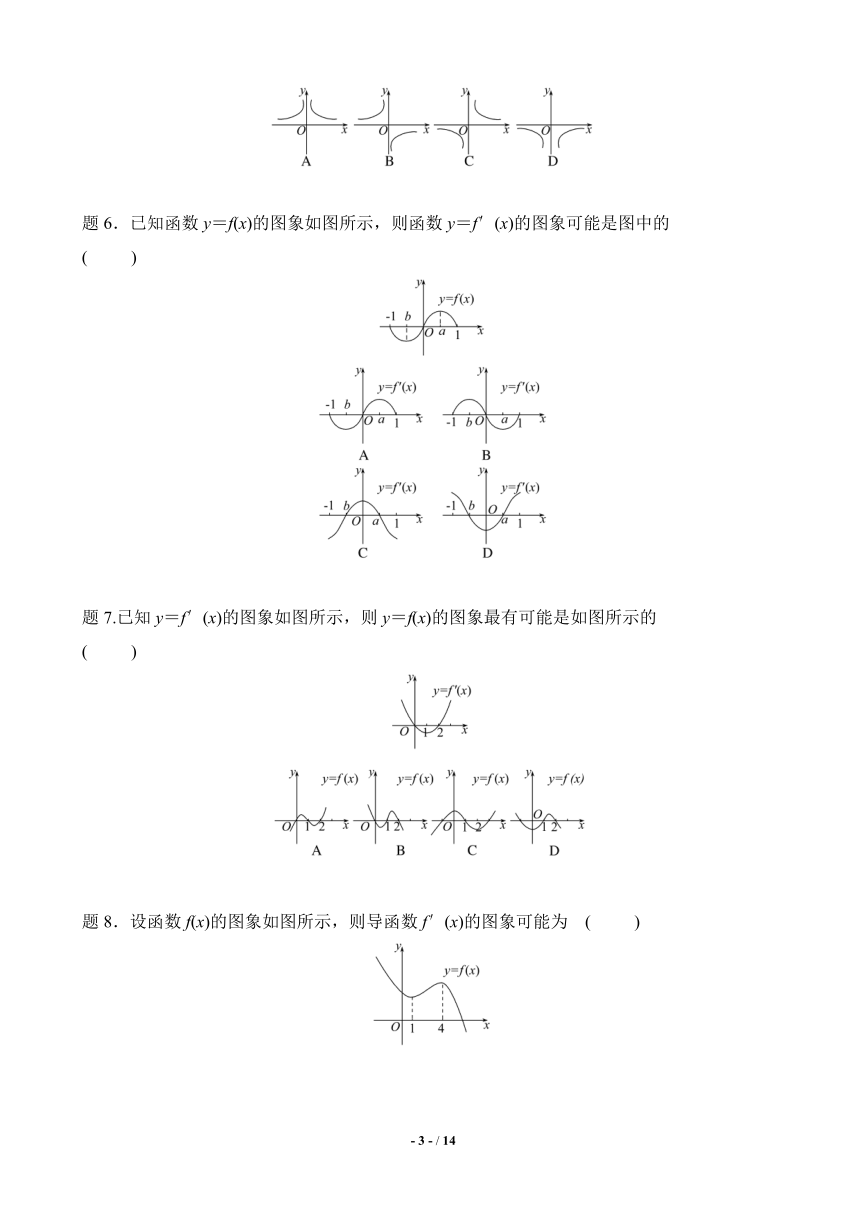
题6.已知函数y=f(x)的图象如图所示,则函数y=f′(x)的图象可能是图中的 ( )
题7.已知y=f′(x)的图象如图所示,则y=f(x)的图象最有可能是如图所示的 ( )
题8.设函数f(x)的图象如图所示,则导函数f′(x)的图象可能为 ( )
类型二 利用导数求函数的单调区间(数学抽象、数学运算)
角度1 不含参数的函数的单调性
【典例】题9.函数y=x2·ex的单调递增区间为________.
题10.求函数y=x2·ex的单调递减区间.
角度2 含参数的函数的单调性
【典例】题11.讨论函数f(x)=x2-a ln x(a≥0)的单调性.
题12.函数f(x)=(x-3)ex的单调递增区间是 ( )
A.(-∞,2) B.(0,3) C.(1,4) D.(2,+∞)
题13.讨论函数f(x)=ax2+x-(a+1)ln x(a≥0)的单调性.
类型三 与单调性有关的参数问题(数学运算、逻辑推理)
【典例】题14.已知函数f(x)=x3-ax-1为单调递增函数,求实数a的取值范围.
题15.已知函数f(x)=-x3+ax2-x-1在(-∞,+∞)上是减函数,则实数a的取值范围是( )
A., B.[-,]
C.(-∞,-),(,+∞) D.(-,)
题16.若函数y=a(x3-x)的单调递减区间为,则a的取值范围是 ( )
A.a>0 B.-11 D.0【课堂检测达标】
题17.函数y=x4-2x2+5的单调递减区间为 ( )
A.(-∞,-1],[0,1] B.[-1,0],[1,+∞)
C.[-1,1] D.(-∞,-1),[1,+∞)
题18.(多选题)设f′(x)是函数f(x)的导函数,将y=f(x)和y=f′(x)的图象画在同一个直角坐标系中,正确的是 ( )
题19.若函数f(x)=x3-ax2-x+6在(0,1)内单调递减,则实数a的取值范围是 ( )
A.[1,+∞) B.a=1 C.(-∞,1] D.(0,1)
题20.已知函数f(x)=x2-x,则f(x)的单调递增区间为________.
题21.求函数f(x)=3x2-2ln x的单调区间.
§5.3.1 导数在研究函数中的应用—单调性答案
目标要求
1、通过实例分析,了解函数的单调性与导数的关系.
2、能利用导数判断函数的单调性、求函数的单调区间.
3、能利用导数研究函数单调性相关的问题.
学科素养目标
通过具体背景与实例的抽象,经历导数模型的建构和利用导数解决实际问题的过程,使学生对变量数学的思想方法(无穷小算法数学)有新的感悟.进一步发展学生的数学思维能力,感受和体会数学产生和发展的规律以及人类智慧和文明的传承,促进学生全面认识数学的价值.也为后继进一步学习微积分等课程打好基础.
导数与函数、方程、不等式及解析几何等相关内容密切相联.具有“集成”的特点,进而,学习本章节有助于学生从整体上理解和把握数学的结构,灵活运用数学的思想和方法,提高分析问题、解决问题的能力.
重点难点
重点:利用导数判断函数的单调性、求函数的单调区间;
难点:能利用导数研究函数单调性相关的问题.
教学过程
基础知识积累
1. 函数f(x)的单调性与导函数f′(x)正负之间的关系
在某个区间(a,b)上的函数y=f(x):
f′(x)的正负 f(x)的单调性
f′(x)>0 函数f(x)在(a,b)上单调递增
f′(x)<0 函数f(x)在(a,b)上单调递减
【课前预习思考】
(1)如果在某个区间内恒有f′(x)=0,那么函数f(x)有什么特性?
提示:f(x)是常数函数.
(2)在区间(a,b)内,f′(x)>0是f(x)在(a,b)上为单调增函数的什么条件?
提示:充分不必要条件,如f(x)=x3在(-∞,+∞)上单调递增,但f′(x)=3x2≥0.
(3)若函数f(x)为可导函数,且在区间(a,b)上是单调递增(或递减)函数,则f′(x)满足什么条件?
提示:f′(x)≥0(或f′(x)≤0).
2.函数图象的变化趋势与导数值大小的关系
一个函数f在某一范围内导数的绝对值为,则
函数值的变化 函数的图象
越大 在这一范围内变化得较快 比较“陡峭”(向上或向下)
越小 在这一范围内变化得较慢 比较“平缓”
【课前预习思考】
某一范围内函数图象比较陡峭,是否导数值就较大?
提示:不是.导数值有正有负,当函数在某一区间为增函数,且图象较为陡峭时,其切线斜率即导数值越来越大;当函数在某一区间为减函数,且图象较为陡峭时,其切线斜率即导数值为负值,其绝对值越来越大,而导数值越来越小.
【课前小题演练】
题1.(多选)下列命题正确的是 ( ).
A.函数f(x)在区间(a,b)上都有f′(x)<0,则函数f(x)在这个区间上单调递减.
B.函数在某一点的导数越大,函数在该点处的切线越“陡峭”.
C.函数在某个区间上变化越快,函数在这个区间上导数的绝对值越大.
D.判断函数单调性时,在区间内的个别点f′(x)=0,不影响函数在此区间的单调性.
【答案】ACD
提示:A√.函数f(x)在区间(a,b)上都有f′(x)<0,所以函数f(x)在这个区间上单调递减,故正确.
B×.切线的“陡峭”程度与|f′(x)|的大小有关,故错误.
C√.函数在某个区间上变化的快慢,和函数导数的绝对值大小一致.
D√.若f′(x)≥0(≤0),则函数f(x)在区间内单调递增(减),故f′(x)=0不影响函数单调性.
题2.函数f(x)=ex-x的单调递增区间为__________.
【解析】因为f(x)=ex-x,所以f′(x)=ex-1.由f′(x)>0得,ex-1>0,即x>0.
所以f(x)的单调递增区间为(0,+∞).
答案:(0,+∞)
题3.求函数y=x2-4x+a的单调区间.
【解析】y′=2x-4,令y′>0,得x>2;令y′<0,得x<2,所以y=x2-4x+a的增区间为(2,+∞),减区间为(-∞,2).
【课堂题组训练】
类型一 导数与函数图象的关系(数学抽象、数学直观)
题4.函数y=f(x)的图象如图所示,则 ( )
A.f′(3)>0 B.f′(3)<0 C.f′(3)=0 D.f′(3)的正负不确定
【解析】选B.由图象可知,函数f(x)在(1,5)上单调递减,则在(1,5)上有f′(x)<0,故f′(3)<0.
题5.函数y=f(x)的图象如图所示,则导函数y=f′(x)的图象可能是 ( )
【解析】选D.因为函数f(x)在(0,+∞),(-∞,0)上都是减函数,
所以当x>0时,f′(x)<0,当x<0时,f′(x)<0.
题6.已知函数y=f(x)的图象如图所示,则函数y=f′(x)的图象可能是图中的 ( )
【解析】选C.由函数y=f(x)的图象的增减变化趋势判断函数y=f′(x)的正、负情况如表:
x (-1,b) (b,a) (a,1)
f(x) ↘ ↗ ↘
f'(x) - + -
由表可知函数y=f′(x)的图象,当x∈(-1,b)时,在x轴下方;当x∈(b,a)时,在x轴上方;当x∈(a,1)时,在x轴下方.
【解题策略提醒】
通过图象研究函数的单调性的方法
(1)观察原函数的图象,重在找出“上升”“下降”产生变化的点,分析函数值的变化趋势;
(2)观察导函数的图象,重在找出导函数图象与x轴的交点,分析导数的正负.
题7.已知y=f′(x)的图象如图所示,则y=f(x)的图象最有可能是如图所示的 ( )
【解析】选C.本题考查根据导函数与原函数的关系判断图象增减的大致趋势.由f′(x)>0(f′(x)<0)的分界点判断原函数在此分界点两侧的图象的上升和下降趋势.由已知可得x的范围和f′(x)的正、负,f(x)的增减变化情况如表所示:
x (-∞,0) (0,2) (2,+∞)
f'(x) + - +
f(x) ↗ ↘ ↗
由表可知f(x)在(-∞,0)上是增函数,在(0,2)上是减函数,在(2,+∞)上是增函数,故满足条件的只有C.
题8.设函数f(x)的图象如图所示,则导函数f′(x)的图象可能为 ( )
【解析】选C.因为f(x)在(-∞,1),(4,+∞)上是减函数,在(1,4)上为增函数,所以当x<1或x>4时,f′(x)<0;当1<x<4时,f′(x)>0.
类型二 利用导数求函数的单调区间(数学抽象、数学运算)
角度1 不含参数的函数的单调性
【典例】题9.函数y=x2·ex的单调递增区间为________.
【思路导引】先求导数,再令导函数>0,解得的区间即为所求.
【解析】y′=2x·ex+x2ex=(x2+2x)ex,由y′>0,ex>0得x2+2x>0,即x>0或x<-2.
答案:(-∞,-2),(0,+∞)
题10.求函数y=x2·ex的单调递减区间.
【解析】y′=2x·ex+x2ex=(x2+2x)ex,由y′<0,ex>0得x2+2x<0,即-2单调递减区间为(0,-2).
角度2 含参数的函数的单调性
【典例】题11.讨论函数f(x)=x2-a ln x(a≥0)的单调性.
【解析】函数f(x)的定义域是(0,+∞),
f′(x)=2x-=,设g(x)=2x2-a,由g(x)=0得2x2=a.当a=0时,f′(x)=2x>0,
函数f(x)在区间(0,+∞)上为增函数;
当a>0时,由g(x)=0得x=或x=-(舍去).
当x∈时,g(x)<0,即f′(x)<0;当x∈时,g(x)>0,即f′(x)>0.
所以当a>0时,函数f(x)在区间上为减函数,在区间上为增函数.
综上,当a=0时,函数f(x)的单调递增区间是(0,+∞);当a>0时,函数f(x)的单调递增区间是,单调递减区间是.
【解题策略提醒】
含有参数的函数单调性问题的处理方法
(1)在判断含有参数的函数的单调性时,不仅要考虑到参数的取值范围,而且要结合函数的定义域来
确定f′(x)的符号,否则会产生错误.
(2)分类讨论是把数学问题划分为若干个局部问题,在每一个局部问题中,原先的不确定因素,就变成了确定性问题,当这些局部问题都解决了,整个问题就解决了.
题12.函数f(x)=(x-3)ex的单调递增区间是 ( )
A.(-∞,2) B.(0,3) C.(1,4) D.(2,+∞)
【解析】选D.因为f′(x)=ex+(x-3)ex=(x-2)ex,由f′(x)>0得(x-2)ex>0,所以x>2.
所以f(x)的单调递增区间为(2,+∞).
题13.讨论函数f(x)=ax2+x-(a+1)ln x(a≥0)的单调性.
【解析】函数f(x)的定义域为(0,+∞),f′(x)=ax+1-=.
(1)当a=0时,f′(x)=,由f′(x)>0,得x>1,由f′(x)<0,得0<x<1.
所以f(x)在(0,1)内为减函数,在(1,+∞)内为增函数.
(2)当a>0时,f′(x)=,因为a>0,所以-<0. 由f′(x)>0,得x>1,
由f′(x)<0,得0<x<1.所以f(x)在(0,1)内为减函数,在(1,+∞)内为增函数.
综上所述,当a≥0时,f(x)在(0,1)内为减函数,在(1,+∞)内为增函数.
类型三 与单调性有关的参数问题(数学运算、逻辑推理)
【典例】题14.已知函数f(x)=x3-ax-1为单调递增函数,求实数a的取值范围.
四步 内容
理解题意 条件:①f(x)=x3-ax-1②f(x)为单调增函数结论:求实数a的取值范围
思路探求 f(x)为单调递增函数→f'(x)≥0恒成立→分离参数求a的范围
书写表达 由已知得f'(x)=3x2-a,因为f(x)在(-∞,+∞)上是单调递增函数,所以f'(x)=3x2-a≥0在(-∞,+∞)上恒成立,即a≤3x2对x∈R恒成立,因为3x2≥0,所以只需a≤0.又因为a=0时,f'(x)=3x2≥0,f(x)=x3-1在R上是增函数,所以a≤0.
题后反思 若函数f(x)在区间(a,b)上是单调递增(或递减)函数,则f'(x)≥0(或f'(x)≤0).
【解题策略提醒】
已知函数y=f(x)在(a,b)上的单调性,求参数的范围的方法
(1)利用集合间的包含关系处理:y=f(x)在(a,b)上单调,则区间(a,b)是相应单调区间的子集;
(2)转化为不等式的恒成立问题:即“若函数单调递增,则f′(x)≥0;若函数单调递减,则f′(x)≤0”来求解,注意此时公式中的等号不能省略,否则漏解;
(3)分离参数法.由f′(x)≥0或f′(x)≤0将所求参数分离到一侧,另一侧为不含参数的函数.只要求出其最值,即可求参数范围.
题15.已知函数f(x)=-x3+ax2-x-1在(-∞,+∞)上是减函数,则实数a的取值范围是( )
A., B.[-,]
C.(-∞,-),(,+∞) D.(-,)
【解析】选B.f′(x)=-3x2+2ax-1≤0在(-∞,+∞)上恒成立,由Δ=4a2-12≤0得-≤a≤.
题16.若函数y=a(x3-x)的单调递减区间为,则a的取值范围是 ( )
A.a>0 B.-11 D.0【解析】选A.因为y′=3a=3a,
当-所以y′≤0,即a≥0,经检验a=0不合题意,所以a>0.
【课堂检测达标】
题17.函数y=x4-2x2+5的单调递减区间为 ( )
A.(-∞,-1],[0,1] B.[-1,0],[1,+∞)
C.[-1,1] D.(-∞,-1),[1,+∞)
【解析】选A.因为y′=4x3-4x=4x(x-1)(x+1),所以令y′<0,则有x(x-1)(x+1)<0,可得x<-1或0题18.(多选题)设f′(x)是函数f(x)的导函数,将y=f(x)和y=f′(x)的图象画在同一个直角坐标系中,正确的是 ( )
【解析】选ABC.A,B,C均有可能;对于D,若C1为导函数,则y=f(x)应为增函数,不符合;若C2为导函数,则y=f(x)应为减函数,也不符合.
题19.若函数f(x)=x3-ax2-x+6在(0,1)内单调递减,则实数a的取值范围是 ( )
A.[1,+∞) B.a=1 C.(-∞,1] D.(0,1)
【解析】选A.因为f′(x)=3x2-2ax-1,且f(x)在(0,1)内单调递减,
所以不等式3x2-2ax-1≤0在(0,1)内恒成立,所以f′(0)≤0,且f′(1)≤0,所以a≥1.
题20.已知函数f(x)=x2-x,则f(x)的单调递增区间为________.
【解析】因为f′(x)=x-1,令f′(x)>0,解得x>1,故f(x)的单调递增区间是(1,+∞).
答案:(1,+∞)
题21.求函数f(x)=3x2-2ln x的单调区间.
【解析】函数f(x)的定义域为(0,+∞),f′(x)=6x-=.令f′(x)>0,即>0,
因为x>0,所以x>,所以函数f(x)的单调递增区间是.令f′(x)<0,即<0,
因为x>0,所以0PAGE
- 2 - / 2
目标要求
1、通过实例分析,了解函数的单调性与导数的关系.
2、能利用导数判断函数的单调性、求函数的单调区间.
3、能利用导数研究函数单调性相关的问题.
学科素养目标
通过具体背景与实例的抽象,经历导数模型的建构和利用导数解决实际问题的过程,使学生对变量数学的思想方法(无穷小算法数学)有新的感悟.进一步发展学生的数学思维能力,感受和体会数学产生和发展的规律以及人类智慧和文明的传承,促进学生全面认识数学的价值.也为后继进一步学习微积分等课程打好基础.
导数与函数、方程、不等式及解析几何等相关内容密切相联.具有“集成”的特点,进而,学习本章节有助于学生从整体上理解和把握数学的结构,灵活运用数学的思想和方法,提高分析问题、解决问题的能力.
重点难点
重点:利用导数判断函数的单调性、求函数的单调区间;
难点:能利用导数研究函数单调性相关的问题.
教学过程
基础知识积累
1. 函数f(x)的单调性与导函数f′(x)正负之间的关系
在某个区间(a,b)上的函数y=f(x):
f′(x)的正负 f(x)的单调性
f′(x)>0 函数f(x)在(a,b)上___________
f′(x)<0 函数f(x)在(a,b)上___________
【课前预习思考】
(1)如果在某个区间内恒有f′(x)=0,那么函数f(x)有什么特性?
(2)在区间(a,b)内,f′(x)>0是f(x)在(a,b)上为单调增函数的什么条件?
(3)若函数f(x)为可导函数,且在区间(a,b)上是单调递增(或递减)函数,则f′(x)满足什么条件?
2.函数图象的变化趋势与导数值大小的关系
一个函数f在某一范围内导数的绝对值为,则
函数值的变化 函数的图象
越大 在这一范围内变化得较快 比较“陡峭”(向上或向下)
越小 在这一范围内变化得较慢 比较“平缓”
【课前预习思考】
某一范围内函数图象比较陡峭,是否导数值就较大?
【课前小题演练】
题1.(多选)下列命题正确的是 ( ).
A.函数f(x)在区间(a,b)上都有f′(x)<0,则函数f(x)在这个区间上单调递减.
B.函数在某一点的导数越大,函数在该点处的切线越“陡峭”.
C.函数在某个区间上变化越快,函数在这个区间上导数的绝对值越大.
D.判断函数单调性时,在区间内的个别点f′(x)=0,不影响函数在此区间的单调性.
题2.函数f(x)=ex-x的单调递增区间为__________.
题3.求函数y=x2-4x+a的单调区间.
【课堂题组训练】
类型一 导数与函数图象的关系(数学抽象、数学直观)
题4.函数y=f(x)的图象如图所示,则 ( )
A.f′(3)>0 B.f′(3)<0 C.f′(3)=0 D.f′(3)的正负不确定
题5.函数y=f(x)的图象如图所示,则导函数y=f′(x)的图象可能是 ( )
题6.已知函数y=f(x)的图象如图所示,则函数y=f′(x)的图象可能是图中的 ( )
题7.已知y=f′(x)的图象如图所示,则y=f(x)的图象最有可能是如图所示的 ( )
题8.设函数f(x)的图象如图所示,则导函数f′(x)的图象可能为 ( )
类型二 利用导数求函数的单调区间(数学抽象、数学运算)
角度1 不含参数的函数的单调性
【典例】题9.函数y=x2·ex的单调递增区间为________.
题10.求函数y=x2·ex的单调递减区间.
角度2 含参数的函数的单调性
【典例】题11.讨论函数f(x)=x2-a ln x(a≥0)的单调性.
题12.函数f(x)=(x-3)ex的单调递增区间是 ( )
A.(-∞,2) B.(0,3) C.(1,4) D.(2,+∞)
题13.讨论函数f(x)=ax2+x-(a+1)ln x(a≥0)的单调性.
类型三 与单调性有关的参数问题(数学运算、逻辑推理)
【典例】题14.已知函数f(x)=x3-ax-1为单调递增函数,求实数a的取值范围.
题15.已知函数f(x)=-x3+ax2-x-1在(-∞,+∞)上是减函数,则实数a的取值范围是( )
A., B.[-,]
C.(-∞,-),(,+∞) D.(-,)
题16.若函数y=a(x3-x)的单调递减区间为,则a的取值范围是 ( )
A.a>0 B.-1
题17.函数y=x4-2x2+5的单调递减区间为 ( )
A.(-∞,-1],[0,1] B.[-1,0],[1,+∞)
C.[-1,1] D.(-∞,-1),[1,+∞)
题18.(多选题)设f′(x)是函数f(x)的导函数,将y=f(x)和y=f′(x)的图象画在同一个直角坐标系中,正确的是 ( )
题19.若函数f(x)=x3-ax2-x+6在(0,1)内单调递减,则实数a的取值范围是 ( )
A.[1,+∞) B.a=1 C.(-∞,1] D.(0,1)
题20.已知函数f(x)=x2-x,则f(x)的单调递增区间为________.
题21.求函数f(x)=3x2-2ln x的单调区间.
§5.3.1 导数在研究函数中的应用—单调性答案
目标要求
1、通过实例分析,了解函数的单调性与导数的关系.
2、能利用导数判断函数的单调性、求函数的单调区间.
3、能利用导数研究函数单调性相关的问题.
学科素养目标
通过具体背景与实例的抽象,经历导数模型的建构和利用导数解决实际问题的过程,使学生对变量数学的思想方法(无穷小算法数学)有新的感悟.进一步发展学生的数学思维能力,感受和体会数学产生和发展的规律以及人类智慧和文明的传承,促进学生全面认识数学的价值.也为后继进一步学习微积分等课程打好基础.
导数与函数、方程、不等式及解析几何等相关内容密切相联.具有“集成”的特点,进而,学习本章节有助于学生从整体上理解和把握数学的结构,灵活运用数学的思想和方法,提高分析问题、解决问题的能力.
重点难点
重点:利用导数判断函数的单调性、求函数的单调区间;
难点:能利用导数研究函数单调性相关的问题.
教学过程
基础知识积累
1. 函数f(x)的单调性与导函数f′(x)正负之间的关系
在某个区间(a,b)上的函数y=f(x):
f′(x)的正负 f(x)的单调性
f′(x)>0 函数f(x)在(a,b)上单调递增
f′(x)<0 函数f(x)在(a,b)上单调递减
【课前预习思考】
(1)如果在某个区间内恒有f′(x)=0,那么函数f(x)有什么特性?
提示:f(x)是常数函数.
(2)在区间(a,b)内,f′(x)>0是f(x)在(a,b)上为单调增函数的什么条件?
提示:充分不必要条件,如f(x)=x3在(-∞,+∞)上单调递增,但f′(x)=3x2≥0.
(3)若函数f(x)为可导函数,且在区间(a,b)上是单调递增(或递减)函数,则f′(x)满足什么条件?
提示:f′(x)≥0(或f′(x)≤0).
2.函数图象的变化趋势与导数值大小的关系
一个函数f在某一范围内导数的绝对值为,则
函数值的变化 函数的图象
越大 在这一范围内变化得较快 比较“陡峭”(向上或向下)
越小 在这一范围内变化得较慢 比较“平缓”
【课前预习思考】
某一范围内函数图象比较陡峭,是否导数值就较大?
提示:不是.导数值有正有负,当函数在某一区间为增函数,且图象较为陡峭时,其切线斜率即导数值越来越大;当函数在某一区间为减函数,且图象较为陡峭时,其切线斜率即导数值为负值,其绝对值越来越大,而导数值越来越小.
【课前小题演练】
题1.(多选)下列命题正确的是 ( ).
A.函数f(x)在区间(a,b)上都有f′(x)<0,则函数f(x)在这个区间上单调递减.
B.函数在某一点的导数越大,函数在该点处的切线越“陡峭”.
C.函数在某个区间上变化越快,函数在这个区间上导数的绝对值越大.
D.判断函数单调性时,在区间内的个别点f′(x)=0,不影响函数在此区间的单调性.
【答案】ACD
提示:A√.函数f(x)在区间(a,b)上都有f′(x)<0,所以函数f(x)在这个区间上单调递减,故正确.
B×.切线的“陡峭”程度与|f′(x)|的大小有关,故错误.
C√.函数在某个区间上变化的快慢,和函数导数的绝对值大小一致.
D√.若f′(x)≥0(≤0),则函数f(x)在区间内单调递增(减),故f′(x)=0不影响函数单调性.
题2.函数f(x)=ex-x的单调递增区间为__________.
【解析】因为f(x)=ex-x,所以f′(x)=ex-1.由f′(x)>0得,ex-1>0,即x>0.
所以f(x)的单调递增区间为(0,+∞).
答案:(0,+∞)
题3.求函数y=x2-4x+a的单调区间.
【解析】y′=2x-4,令y′>0,得x>2;令y′<0,得x<2,所以y=x2-4x+a的增区间为(2,+∞),减区间为(-∞,2).
【课堂题组训练】
类型一 导数与函数图象的关系(数学抽象、数学直观)
题4.函数y=f(x)的图象如图所示,则 ( )
A.f′(3)>0 B.f′(3)<0 C.f′(3)=0 D.f′(3)的正负不确定
【解析】选B.由图象可知,函数f(x)在(1,5)上单调递减,则在(1,5)上有f′(x)<0,故f′(3)<0.
题5.函数y=f(x)的图象如图所示,则导函数y=f′(x)的图象可能是 ( )
【解析】选D.因为函数f(x)在(0,+∞),(-∞,0)上都是减函数,
所以当x>0时,f′(x)<0,当x<0时,f′(x)<0.
题6.已知函数y=f(x)的图象如图所示,则函数y=f′(x)的图象可能是图中的 ( )
【解析】选C.由函数y=f(x)的图象的增减变化趋势判断函数y=f′(x)的正、负情况如表:
x (-1,b) (b,a) (a,1)
f(x) ↘ ↗ ↘
f'(x) - + -
由表可知函数y=f′(x)的图象,当x∈(-1,b)时,在x轴下方;当x∈(b,a)时,在x轴上方;当x∈(a,1)时,在x轴下方.
【解题策略提醒】
通过图象研究函数的单调性的方法
(1)观察原函数的图象,重在找出“上升”“下降”产生变化的点,分析函数值的变化趋势;
(2)观察导函数的图象,重在找出导函数图象与x轴的交点,分析导数的正负.
题7.已知y=f′(x)的图象如图所示,则y=f(x)的图象最有可能是如图所示的 ( )
【解析】选C.本题考查根据导函数与原函数的关系判断图象增减的大致趋势.由f′(x)>0(f′(x)<0)的分界点判断原函数在此分界点两侧的图象的上升和下降趋势.由已知可得x的范围和f′(x)的正、负,f(x)的增减变化情况如表所示:
x (-∞,0) (0,2) (2,+∞)
f'(x) + - +
f(x) ↗ ↘ ↗
由表可知f(x)在(-∞,0)上是增函数,在(0,2)上是减函数,在(2,+∞)上是增函数,故满足条件的只有C.
题8.设函数f(x)的图象如图所示,则导函数f′(x)的图象可能为 ( )
【解析】选C.因为f(x)在(-∞,1),(4,+∞)上是减函数,在(1,4)上为增函数,所以当x<1或x>4时,f′(x)<0;当1<x<4时,f′(x)>0.
类型二 利用导数求函数的单调区间(数学抽象、数学运算)
角度1 不含参数的函数的单调性
【典例】题9.函数y=x2·ex的单调递增区间为________.
【思路导引】先求导数,再令导函数>0,解得的区间即为所求.
【解析】y′=2x·ex+x2ex=(x2+2x)ex,由y′>0,ex>0得x2+2x>0,即x>0或x<-2.
答案:(-∞,-2),(0,+∞)
题10.求函数y=x2·ex的单调递减区间.
【解析】y′=2x·ex+x2ex=(x2+2x)ex,由y′<0,ex>0得x2+2x<0,即-2
角度2 含参数的函数的单调性
【典例】题11.讨论函数f(x)=x2-a ln x(a≥0)的单调性.
【解析】函数f(x)的定义域是(0,+∞),
f′(x)=2x-=,设g(x)=2x2-a,由g(x)=0得2x2=a.当a=0时,f′(x)=2x>0,
函数f(x)在区间(0,+∞)上为增函数;
当a>0时,由g(x)=0得x=或x=-(舍去).
当x∈时,g(x)<0,即f′(x)<0;当x∈时,g(x)>0,即f′(x)>0.
所以当a>0时,函数f(x)在区间上为减函数,在区间上为增函数.
综上,当a=0时,函数f(x)的单调递增区间是(0,+∞);当a>0时,函数f(x)的单调递增区间是,单调递减区间是.
【解题策略提醒】
含有参数的函数单调性问题的处理方法
(1)在判断含有参数的函数的单调性时,不仅要考虑到参数的取值范围,而且要结合函数的定义域来
确定f′(x)的符号,否则会产生错误.
(2)分类讨论是把数学问题划分为若干个局部问题,在每一个局部问题中,原先的不确定因素,就变成了确定性问题,当这些局部问题都解决了,整个问题就解决了.
题12.函数f(x)=(x-3)ex的单调递增区间是 ( )
A.(-∞,2) B.(0,3) C.(1,4) D.(2,+∞)
【解析】选D.因为f′(x)=ex+(x-3)ex=(x-2)ex,由f′(x)>0得(x-2)ex>0,所以x>2.
所以f(x)的单调递增区间为(2,+∞).
题13.讨论函数f(x)=ax2+x-(a+1)ln x(a≥0)的单调性.
【解析】函数f(x)的定义域为(0,+∞),f′(x)=ax+1-=.
(1)当a=0时,f′(x)=,由f′(x)>0,得x>1,由f′(x)<0,得0<x<1.
所以f(x)在(0,1)内为减函数,在(1,+∞)内为增函数.
(2)当a>0时,f′(x)=,因为a>0,所以-<0. 由f′(x)>0,得x>1,
由f′(x)<0,得0<x<1.所以f(x)在(0,1)内为减函数,在(1,+∞)内为增函数.
综上所述,当a≥0时,f(x)在(0,1)内为减函数,在(1,+∞)内为增函数.
类型三 与单调性有关的参数问题(数学运算、逻辑推理)
【典例】题14.已知函数f(x)=x3-ax-1为单调递增函数,求实数a的取值范围.
四步 内容
理解题意 条件:①f(x)=x3-ax-1②f(x)为单调增函数结论:求实数a的取值范围
思路探求 f(x)为单调递增函数→f'(x)≥0恒成立→分离参数求a的范围
书写表达 由已知得f'(x)=3x2-a,因为f(x)在(-∞,+∞)上是单调递增函数,所以f'(x)=3x2-a≥0在(-∞,+∞)上恒成立,即a≤3x2对x∈R恒成立,因为3x2≥0,所以只需a≤0.又因为a=0时,f'(x)=3x2≥0,f(x)=x3-1在R上是增函数,所以a≤0.
题后反思 若函数f(x)在区间(a,b)上是单调递增(或递减)函数,则f'(x)≥0(或f'(x)≤0).
【解题策略提醒】
已知函数y=f(x)在(a,b)上的单调性,求参数的范围的方法
(1)利用集合间的包含关系处理:y=f(x)在(a,b)上单调,则区间(a,b)是相应单调区间的子集;
(2)转化为不等式的恒成立问题:即“若函数单调递增,则f′(x)≥0;若函数单调递减,则f′(x)≤0”来求解,注意此时公式中的等号不能省略,否则漏解;
(3)分离参数法.由f′(x)≥0或f′(x)≤0将所求参数分离到一侧,另一侧为不含参数的函数.只要求出其最值,即可求参数范围.
题15.已知函数f(x)=-x3+ax2-x-1在(-∞,+∞)上是减函数,则实数a的取值范围是( )
A., B.[-,]
C.(-∞,-),(,+∞) D.(-,)
【解析】选B.f′(x)=-3x2+2ax-1≤0在(-∞,+∞)上恒成立,由Δ=4a2-12≤0得-≤a≤.
题16.若函数y=a(x3-x)的单调递减区间为,则a的取值范围是 ( )
A.a>0 B.-1
当-
【课堂检测达标】
题17.函数y=x4-2x2+5的单调递减区间为 ( )
A.(-∞,-1],[0,1] B.[-1,0],[1,+∞)
C.[-1,1] D.(-∞,-1),[1,+∞)
【解析】选A.因为y′=4x3-4x=4x(x-1)(x+1),所以令y′<0,则有x(x-1)(x+1)<0,可得x<-1或0
【解析】选ABC.A,B,C均有可能;对于D,若C1为导函数,则y=f(x)应为增函数,不符合;若C2为导函数,则y=f(x)应为减函数,也不符合.
题19.若函数f(x)=x3-ax2-x+6在(0,1)内单调递减,则实数a的取值范围是 ( )
A.[1,+∞) B.a=1 C.(-∞,1] D.(0,1)
【解析】选A.因为f′(x)=3x2-2ax-1,且f(x)在(0,1)内单调递减,
所以不等式3x2-2ax-1≤0在(0,1)内恒成立,所以f′(0)≤0,且f′(1)≤0,所以a≥1.
题20.已知函数f(x)=x2-x,则f(x)的单调递增区间为________.
【解析】因为f′(x)=x-1,令f′(x)>0,解得x>1,故f(x)的单调递增区间是(1,+∞).
答案:(1,+∞)
题21.求函数f(x)=3x2-2ln x的单调区间.
【解析】函数f(x)的定义域为(0,+∞),f′(x)=6x-=.令f′(x)>0,即>0,
因为x>0,所以x>,所以函数f(x)的单调递增区间是.令f′(x)<0,即<0,
因为x>0,所以0
- 2 - / 2
