圆锥曲线最值[下学期]
图片预览




文档简介
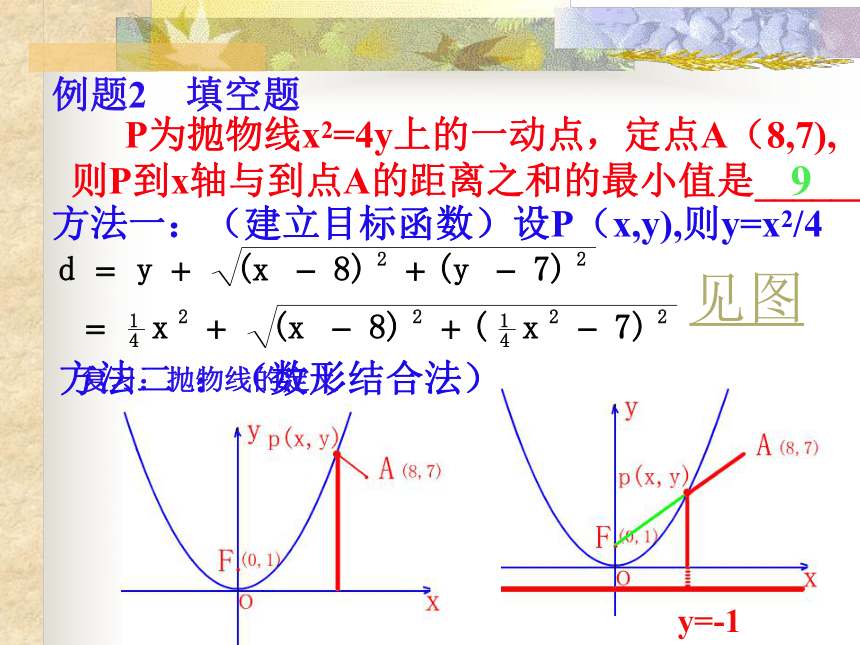
课件14张PPT。圆锥曲线中的最值问题思考:求圆锥曲线的最值常用哪些方法? [例1] 选择题
1)点P在抛物线y2=x上,定点
A(3,0),则|PA|的最小值是( )方法一:(建立目标函数)设P(x,y) 则y2=x.B方法二:过A作同心圆,当圆
与抛物线相切时,P到A点的
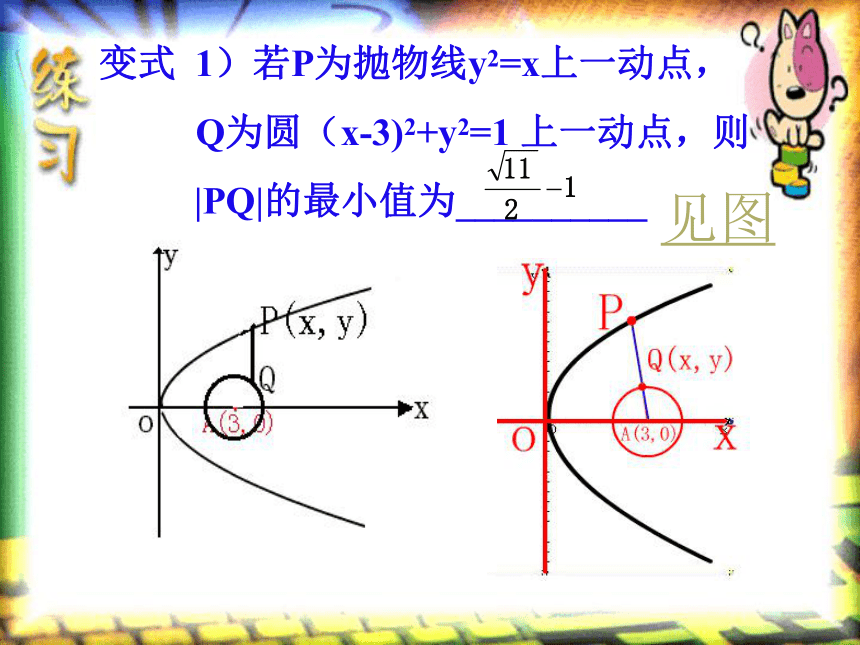
距离最小,设为r见图答案选(B)变式 1)若P为抛物线y2=x上一动点,
Q为圆(x-3)2+y2=1 上一动点,则
|PQ|的最小值为__________
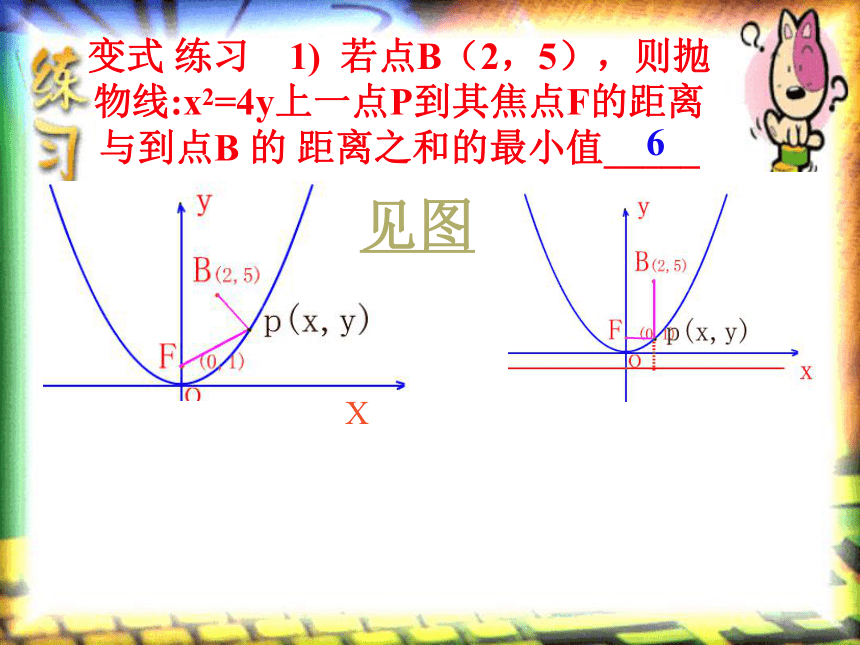
见图方法一:(建立目标函数)设P(x,y),则y=x2/4方法二 :(数形结合法)9见图 y=-1复习:抛物线的定义变式 练习 1) 若点B(2,5),则抛
物线:x2=4y上一点P到其焦点F的距离
与到点B 的 距离之和的最小值_____ 6X见图变式练习2)已知椭圆 :9x2+25y2=225的左焦点
为F,定点B(2,-1),在椭圆上求一点P,使
|PF|+0.8|PB |的值最小,则P点坐标是_______oxyP(x,y)分析:本题中的系数0.8有何意义?注意到:a=5;b=3;∴c=4;离心率 e=0.8设P(x,y)到左准线的距离为|PM|
则:|PF|=0.8|PM|∴ |PF|+0.8|PB|
=0.8|PM|+0.8|PB|
=0.8(|PM|+|PB|)从而只要求P点到B点与左准线的距离
之和的最小值,这样就化归为变式1)
同类问题。为止,过点B作BM0垂直
于左准线于M0,交椭圆于P0,则P0
为所求易求得P的坐标是: 见图例3 设P为抛物线 y= x2上的一动点,求P点到
直线L: 3x-4y-6=0的距离的最小值。 解法1:设P(x,x2),P到直线L:3x-4y-6=0的距离d。
解法二:当L平移到与抛物线y=x2只有一个公共点时,设此时的直线为L1,其方程为3x-4y-b=0。
则L与L1的距离即为所求。 见图复习:两平行线L1 : Ax +By+C 1=0, L 2:
Ax+By+C 2=0 的距离
d=__________掌握求圆锥曲线中的有关最值的基本方法仍
然是建立目标函数,利用函数的性质或不等
式的性质以及通过设参、换元等途径来解决。2.解析几何是研究“形”的科学,因此,在求圆
锥曲线的最值问题时要善于结合图形,通过
数形结合将抽象的问题、繁杂的问题化归为
动态的形的问题,从而使问题顺利解决。 3.有些最值问题要灵活地利用圆锥曲线的定义
将折线段和的问题化归为平面几何中的直线
段最短来解决。 上述解法对吗? 点评:
1) 求曲线上一点到已知点的距离的最大
(小)值,可过已知点作同心圆,当圆与
曲线恰好相切时,则此公共点到已知点的
距离最大(小)。 2) 求曲线上一动点到一已知圆上一动点的距离的最大(小)值问题,常转化为求曲线上的动点到圆心的距离的最大(小)值问题。点评:一般,设A为曲线含焦点F的区域内一点
在曲线上求一点P,使|PF|+e|PA| 的值最小,都
可以过点A作与焦点F相应准线的垂线,则垂线
段与曲线的交点即为所求之点。类似练习:设F是双曲线 :5x2-4y2=20 的右焦点,定点
M(6,2),在双曲线的右支上求一点P,使|PM|+|PF| × 2/3
最小。(课后思考)
1)点P在抛物线y2=x上,定点
A(3,0),则|PA|的最小值是( )方法一:(建立目标函数)设P(x,y) 则y2=x.B方法二:过A作同心圆,当圆
与抛物线相切时,P到A点的
距离最小,设为r见图答案选(B)变式 1)若P为抛物线y2=x上一动点,
Q为圆(x-3)2+y2=1 上一动点,则
|PQ|的最小值为__________
见图方法一:(建立目标函数)设P(x,y),则y=x2/4方法二 :(数形结合法)9见图 y=-1复习:抛物线的定义变式 练习 1) 若点B(2,5),则抛
物线:x2=4y上一点P到其焦点F的距离
与到点B 的 距离之和的最小值_____ 6X见图变式练习2)已知椭圆 :9x2+25y2=225的左焦点
为F,定点B(2,-1),在椭圆上求一点P,使
|PF|+0.8|PB |的值最小,则P点坐标是_______oxyP(x,y)分析:本题中的系数0.8有何意义?注意到:a=5;b=3;∴c=4;离心率 e=0.8设P(x,y)到左准线的距离为|PM|
则:|PF|=0.8|PM|∴ |PF|+0.8|PB|
=0.8|PM|+0.8|PB|
=0.8(|PM|+|PB|)从而只要求P点到B点与左准线的距离
之和的最小值,这样就化归为变式1)
同类问题。为止,过点B作BM0垂直
于左准线于M0,交椭圆于P0,则P0
为所求易求得P的坐标是: 见图例3 设P为抛物线 y= x2上的一动点,求P点到
直线L: 3x-4y-6=0的距离的最小值。 解法1:设P(x,x2),P到直线L:3x-4y-6=0的距离d。
解法二:当L平移到与抛物线y=x2只有一个公共点时,设此时的直线为L1,其方程为3x-4y-b=0。
则L与L1的距离即为所求。 见图复习:两平行线L1 : Ax +By+C 1=0, L 2:
Ax+By+C 2=0 的距离
d=__________掌握求圆锥曲线中的有关最值的基本方法仍
然是建立目标函数,利用函数的性质或不等
式的性质以及通过设参、换元等途径来解决。2.解析几何是研究“形”的科学,因此,在求圆
锥曲线的最值问题时要善于结合图形,通过
数形结合将抽象的问题、繁杂的问题化归为
动态的形的问题,从而使问题顺利解决。 3.有些最值问题要灵活地利用圆锥曲线的定义
将折线段和的问题化归为平面几何中的直线
段最短来解决。 上述解法对吗? 点评:
1) 求曲线上一点到已知点的距离的最大
(小)值,可过已知点作同心圆,当圆与
曲线恰好相切时,则此公共点到已知点的
距离最大(小)。 2) 求曲线上一动点到一已知圆上一动点的距离的最大(小)值问题,常转化为求曲线上的动点到圆心的距离的最大(小)值问题。点评:一般,设A为曲线含焦点F的区域内一点
在曲线上求一点P,使|PF|+e|PA| 的值最小,都
可以过点A作与焦点F相应准线的垂线,则垂线
段与曲线的交点即为所求之点。类似练习:设F是双曲线 :5x2-4y2=20 的右焦点,定点
M(6,2),在双曲线的右支上求一点P,使|PM|+|PF| × 2/3
最小。(课后思考)
