第五章 三角函数 单元检测-2022-2023学年高一上学期数学人教A版(2019)必修第一册(含答案)
文档属性
| 名称 | 第五章 三角函数 单元检测-2022-2023学年高一上学期数学人教A版(2019)必修第一册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 455.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 13:51:52 | ||
图片预览



文档简介
第五章 三角函数单元检测
一、单选题
1.电流强度(安)随时间(秒)变化的函数的图像如图所示,则当秒时,电流强度是( )
A.10安 B.5安
C.安 D.-5安
2.已知,则( )
A. B. C.1 D.
3.已知,,则的值为( )
A. B. C. D.
4.为了得到函数的图象,可以将函数的图象( )
A.向右平移个单位长度 B.向右平移个单位长度
C.向左平移个单位长度 D.向左平移个单位长度
5.已知函数的最小正周期为,将函数的图象向左平移个单位长度后,再将图象上的所有点的纵坐标缩短为原来的,得到函数的图象,则函数的最小值为( )
A.4 B.-4 C. D.
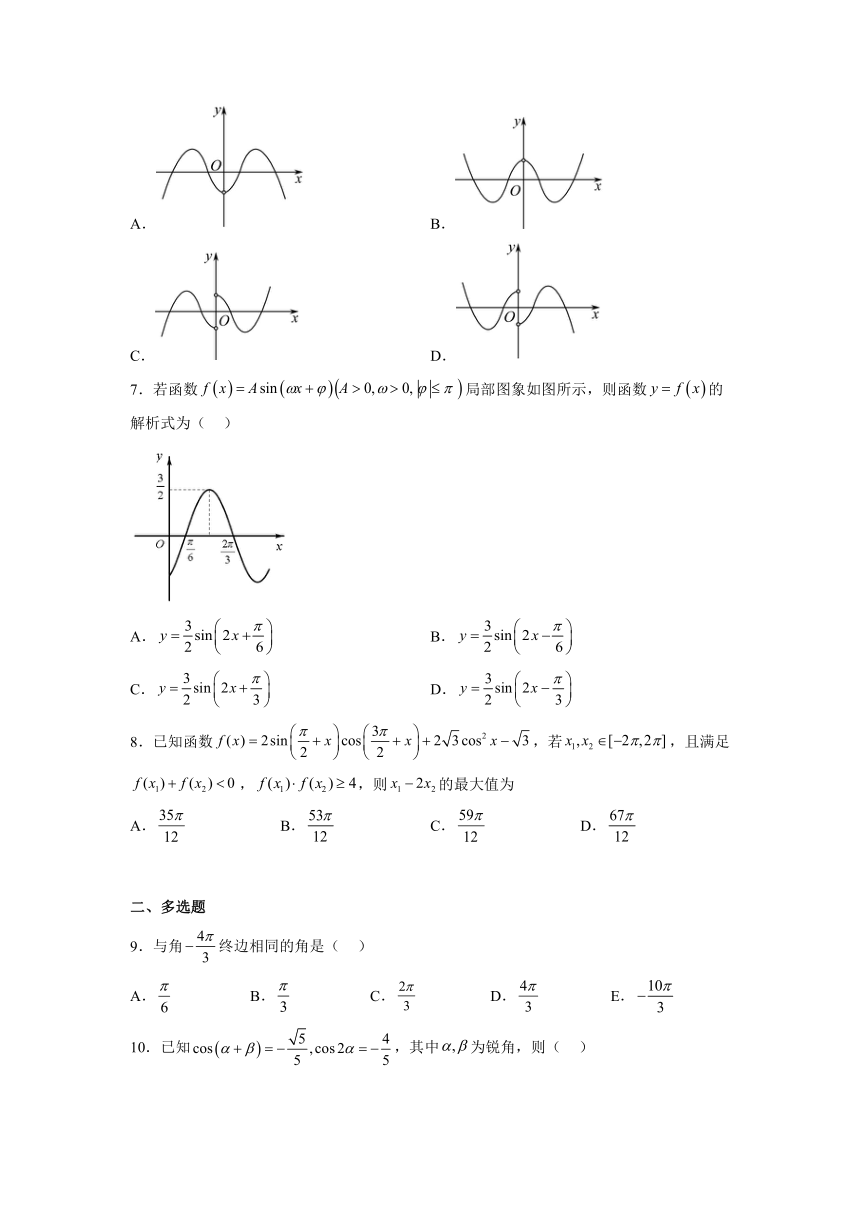
6.函数的部分图象大致为( )
A. B.
C. D.
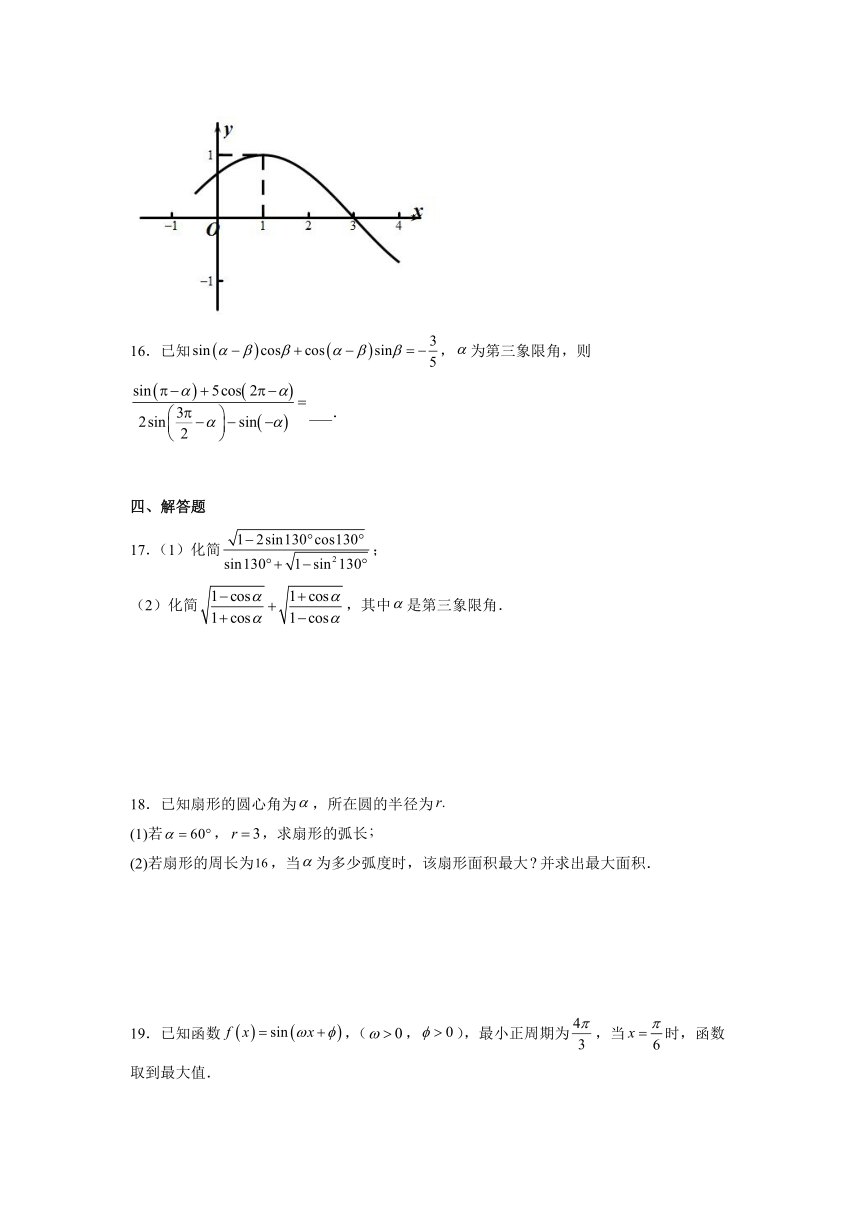
7.若函数局部图象如图所示,则函数的解析式为( )
A. B.
C. D.
8.已知函数,若,且满足,,则的最大值为
A. B. C. D.
二、多选题
9.与角终边相同的角是( )
A. B. C. D. E.
10.已知,其中为锐角,则( )
A. B.
C. D.
11.已知函数,下列四个结论正确的是( )
A.函数在区间上是增函数
B.点是函数图像的一个对称中心
C.函数的图像可以由函数的图像向左平移得到
D.若,则的值域为
12.已知函数的部分图像如图所示,将的图像向左平移个单位长度,再向上平移1个单位长度后得到函数的图像,则( )
A. B.
C.的图像关于点对称 D.在上单调递减
三、填空题
13.(tan50°+tan60°)sin20°=___________.
14.已知函数f(x)="2" sin ωx(ω>0)在区间上的最小值是-2,则ω的最小值为____.
15.函数的部分图象如图所示,则_________.
16.已知,为第三象限角,则___.
四、解答题
17.(1)化简;
(2)化简,其中是第三象限角.
18.已知扇形的圆心角为,所在圆的半径为
(1)若,,求扇形的弧长
(2)若扇形的周长为,当为多少弧度时,该扇形面积最大并求出最大面积.
19.已知函数,(,),最小正周期为,当时,函数取到最大值.
(1)求函数的单调递增区间;
(2)当时,若函数在区间上的值域为,求a,b的值.
20.已知角满足.
(1)求的值;
(2)若角是第三象限角,,求的值.
21.已知函数.
(1)求函数f(x)的单调递增区间;
(2)函数f(x)的图象上所有点的横坐标扩大到原来的2倍,再向右平移个单位长度,得g(x)的图象,求函数y=g(x)在x∈[0,π]上的最大值及最小值.
22.建设生态文明是关系人民福祉、关乎民族未来的长远大计.某市通宵营业的大型商场,为响应国家节能减排的号召,在气温低于时,才开放中央空调,否则关闭中央空调.如图是该市冬季某一天的气温(单位:)随时间(,单位:小时)的大致变化曲线,若该曲线近似满足关系.
(1)求的表达式;
(2)请根据(1)的结论,求该商场的中央空调在一天内开启的时长
答案
1.D
2.A
3.B
4.A
5.D
6.B
7.D
8.B
9.CE
10.AB
11.AB
12.AD
13.1
14.
15.
16.
17.(1)原式,
∵,
∴原式;
(2)
由题可得,,,
∴原式.
18.(1)设扇形的弧长为.,即,.
(2)由题设条件知,,
因此扇形的面积
当时,有最大值,此时,
当时,扇形的面积最大,最大面积是.
19.(1)因为函数,(,),最小正周期为,所以 ,则,
当时,函数取到最大值为1,即,;所以,函数,
令,解得,所以函数的增区间为:.
(2)函数,();
,则,
当,即时,在区间上取得最小值为1,即;
当,即时,在区间上取得最大值为3,即;
,解得.
20.(1)由题意和同角三角函数基本关系式,有,
消去得,解得或,
当角是第一象限角时,,
因为角是第三象限角,.
(2)由题意可得,
因为角是第三象限角,
所以,所以.
21.(1)利用三角函数恒等变换的应用化简函数解析式可得f(x)=sin(2x﹣),由,即可解得函数f(x)的单调递增区间.
(2)利用函数y=Asin(ωx+φ)的图象变换可得g(x)=sin(x﹣),由x∈[0,π]得:,利用正弦函数的图象即可解得函数y=g(x)在x∈[0,π]上的最大值及最小值.
解:(1)∵,
∴由,得,
∴函数f(x)的单调递增区间为:.
(2)函数f(x)的图象上所有点的横坐标扩大到原来的2倍,再向右平移个单位,得,
∵x∈[0,π]得:,
∴.
∴当x=0时,有最小值,
当时,有最大值1.
22.因为图像上最低点坐标为,
与之相邻的最高点坐标为,
所以,,,
所以,解得.
所以,.
(2)由(1)得,,所以,
所以,解得,
因为,所以,.
所以该商场的中央空调应在本天内开启时长为8小时
一、单选题
1.电流强度(安)随时间(秒)变化的函数的图像如图所示,则当秒时,电流强度是( )
A.10安 B.5安
C.安 D.-5安
2.已知,则( )
A. B. C.1 D.
3.已知,,则的值为( )
A. B. C. D.
4.为了得到函数的图象,可以将函数的图象( )
A.向右平移个单位长度 B.向右平移个单位长度
C.向左平移个单位长度 D.向左平移个单位长度
5.已知函数的最小正周期为,将函数的图象向左平移个单位长度后,再将图象上的所有点的纵坐标缩短为原来的,得到函数的图象,则函数的最小值为( )
A.4 B.-4 C. D.
6.函数的部分图象大致为( )
A. B.
C. D.
7.若函数局部图象如图所示,则函数的解析式为( )
A. B.
C. D.
8.已知函数,若,且满足,,则的最大值为
A. B. C. D.
二、多选题
9.与角终边相同的角是( )
A. B. C. D. E.
10.已知,其中为锐角,则( )
A. B.
C. D.
11.已知函数,下列四个结论正确的是( )
A.函数在区间上是增函数
B.点是函数图像的一个对称中心
C.函数的图像可以由函数的图像向左平移得到
D.若,则的值域为
12.已知函数的部分图像如图所示,将的图像向左平移个单位长度,再向上平移1个单位长度后得到函数的图像,则( )
A. B.
C.的图像关于点对称 D.在上单调递减
三、填空题
13.(tan50°+tan60°)sin20°=___________.
14.已知函数f(x)="2" sin ωx(ω>0)在区间上的最小值是-2,则ω的最小值为____.
15.函数的部分图象如图所示,则_________.
16.已知,为第三象限角,则___.
四、解答题
17.(1)化简;
(2)化简,其中是第三象限角.
18.已知扇形的圆心角为,所在圆的半径为
(1)若,,求扇形的弧长
(2)若扇形的周长为,当为多少弧度时,该扇形面积最大并求出最大面积.
19.已知函数,(,),最小正周期为,当时,函数取到最大值.
(1)求函数的单调递增区间;
(2)当时,若函数在区间上的值域为,求a,b的值.
20.已知角满足.
(1)求的值;
(2)若角是第三象限角,,求的值.
21.已知函数.
(1)求函数f(x)的单调递增区间;
(2)函数f(x)的图象上所有点的横坐标扩大到原来的2倍,再向右平移个单位长度,得g(x)的图象,求函数y=g(x)在x∈[0,π]上的最大值及最小值.
22.建设生态文明是关系人民福祉、关乎民族未来的长远大计.某市通宵营业的大型商场,为响应国家节能减排的号召,在气温低于时,才开放中央空调,否则关闭中央空调.如图是该市冬季某一天的气温(单位:)随时间(,单位:小时)的大致变化曲线,若该曲线近似满足关系.
(1)求的表达式;
(2)请根据(1)的结论,求该商场的中央空调在一天内开启的时长
答案
1.D
2.A
3.B
4.A
5.D
6.B
7.D
8.B
9.CE
10.AB
11.AB
12.AD
13.1
14.
15.
16.
17.(1)原式,
∵,
∴原式;
(2)
由题可得,,,
∴原式.
18.(1)设扇形的弧长为.,即,.
(2)由题设条件知,,
因此扇形的面积
当时,有最大值,此时,
当时,扇形的面积最大,最大面积是.
19.(1)因为函数,(,),最小正周期为,所以 ,则,
当时,函数取到最大值为1,即,;所以,函数,
令,解得,所以函数的增区间为:.
(2)函数,();
,则,
当,即时,在区间上取得最小值为1,即;
当,即时,在区间上取得最大值为3,即;
,解得.
20.(1)由题意和同角三角函数基本关系式,有,
消去得,解得或,
当角是第一象限角时,,
因为角是第三象限角,.
(2)由题意可得,
因为角是第三象限角,
所以,所以.
21.(1)利用三角函数恒等变换的应用化简函数解析式可得f(x)=sin(2x﹣),由,即可解得函数f(x)的单调递增区间.
(2)利用函数y=Asin(ωx+φ)的图象变换可得g(x)=sin(x﹣),由x∈[0,π]得:,利用正弦函数的图象即可解得函数y=g(x)在x∈[0,π]上的最大值及最小值.
解:(1)∵,
∴由,得,
∴函数f(x)的单调递增区间为:.
(2)函数f(x)的图象上所有点的横坐标扩大到原来的2倍,再向右平移个单位,得,
∵x∈[0,π]得:,
∴.
∴当x=0时,有最小值,
当时,有最大值1.
22.因为图像上最低点坐标为,
与之相邻的最高点坐标为,
所以,,,
所以,解得.
所以,.
(2)由(1)得,,所以,
所以,解得,
因为,所以,.
所以该商场的中央空调应在本天内开启时长为8小时
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
