9年级数学苏科版下册课件第6单元《6.4探索三角形相似的条件》 课件(共16张PPT)
文档属性
| 名称 | 9年级数学苏科版下册课件第6单元《6.4探索三角形相似的条件》 课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 454.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 08:02:56 | ||
图片预览





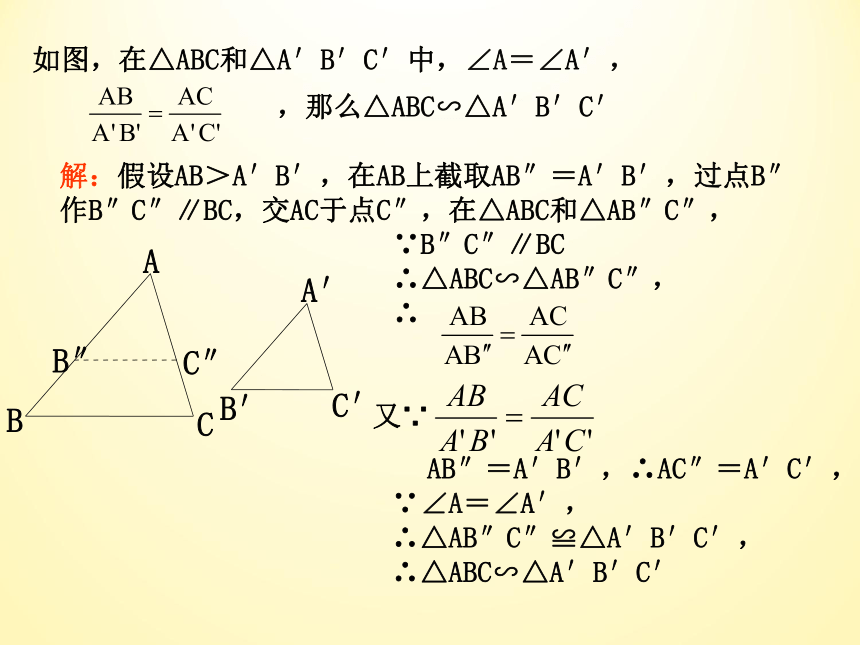
文档简介
(共16张PPT)
探索三角形相似的条件
1.什么叫相似三角形?
2. 相似三角形有哪些特征?
A
B
C
D
E
F
复习回顾
(2) 两角分别对应相等的两个三角形相似。
(1)平行于三角形一边的直线与其他两边(或两边的延长线)相交,所截得的三角形与原三角形相似。
3. 如何判断两个三角形相似?
情境创设:
当两个三角形的两条边及其夹角对应相等时,这两个三角形全等。相应地,我们探索两个三角形相似,可以从哪几个方面考虑找出条件?
1、如图,在△ABC和△A′B′C′中,∠A=∠A′, ,
比较∠B和∠B′的大小.由此,你能判断
△ABC和△A′B′C′相似吗?为什么?
A
B
C
A′
B′
C′
合作探究
2、在上题的条件下,设
改变k的值的大小,( ∠A=∠A′不变)再试一试,你能判断△ABC与△A′B′C′相似吗?
A
B
C
A′
B′
C′
B″
C″
如图,在△ABC和△A′B′C′中,∠A=∠A′,
,那么△ABC∽△A′B′C′
解:假设AB>A′B′,在AB上截取AB″=A′B′,过点B″
作B″C″∥BC,交AC于点C″,在△ABC和△AB″C″,
∵B″C″∥BC
∴△ABC∽△AB″C″,
∴
又∵
AB″=A′B′,∴AC″=A′C′,
∵∠A=∠A′,
∴△AB″C″≌△A′B′C′,
∴△ABC∽△A′B′C′
A
B
C
A′
B′
C′
B″
C″
判定两个三角形相似的方法:
两边对应成比例且夹角相等的两个三角形相似。
几何语言:
∵在△ABC和△A′B′C′中,
∠A=∠A′,
∴△ABC∽△A′B′C′
A
B
C
A′
B′
C′
归纳总结
如图,在△ABC和△A′B′C′中,
∠B=∠B′,要使△ABC∽△A′B′C′,
还需要添加什么条件?
A
B
C
A′
B′
C′
自主展示
例题
如图,在△ABC中,AB=4cm , AC=2cm。
(1)在AB上取一点D,当AD=_____cm时, △ACD∽△ABC;
(2)在AC的延长线上取一点E,当CE=____cm时, △AEB∽△ABC;
D
E
此时,BE与DC有怎样的位置关系?为什么?
思考探索
1、如图,在△ABC中,D在AB上,
要说明△ACD∽△ABC相似,
已经具备了条件 ,
还需添加的条件是 ,
或 或 .
A
C
D
B
随堂练习
A
E
D
C
B
2、如图, 若AD·AB=AE·AC,则△_______∽△______,
且∠B=_____.
3、如图,已知 ,
试求
的值.
A
D
E
C
B
1. 三角形相似的判定方法有哪些?
2.你有哪些收获?
谢谢合作!
本节随堂练习
探索三角形相似的条件
1.什么叫相似三角形?
2. 相似三角形有哪些特征?
A
B
C
D
E
F
复习回顾
(2) 两角分别对应相等的两个三角形相似。
(1)平行于三角形一边的直线与其他两边(或两边的延长线)相交,所截得的三角形与原三角形相似。
3. 如何判断两个三角形相似?
情境创设:
当两个三角形的两条边及其夹角对应相等时,这两个三角形全等。相应地,我们探索两个三角形相似,可以从哪几个方面考虑找出条件?
1、如图,在△ABC和△A′B′C′中,∠A=∠A′, ,
比较∠B和∠B′的大小.由此,你能判断
△ABC和△A′B′C′相似吗?为什么?
A
B
C
A′
B′
C′
合作探究
2、在上题的条件下,设
改变k的值的大小,( ∠A=∠A′不变)再试一试,你能判断△ABC与△A′B′C′相似吗?
A
B
C
A′
B′
C′
B″
C″
如图,在△ABC和△A′B′C′中,∠A=∠A′,
,那么△ABC∽△A′B′C′
解:假设AB>A′B′,在AB上截取AB″=A′B′,过点B″
作B″C″∥BC,交AC于点C″,在△ABC和△AB″C″,
∵B″C″∥BC
∴△ABC∽△AB″C″,
∴
又∵
AB″=A′B′,∴AC″=A′C′,
∵∠A=∠A′,
∴△AB″C″≌△A′B′C′,
∴△ABC∽△A′B′C′
A
B
C
A′
B′
C′
B″
C″
判定两个三角形相似的方法:
两边对应成比例且夹角相等的两个三角形相似。
几何语言:
∵在△ABC和△A′B′C′中,
∠A=∠A′,
∴△ABC∽△A′B′C′
A
B
C
A′
B′
C′
归纳总结
如图,在△ABC和△A′B′C′中,
∠B=∠B′,要使△ABC∽△A′B′C′,
还需要添加什么条件?
A
B
C
A′
B′
C′
自主展示
例题
如图,在△ABC中,AB=4cm , AC=2cm。
(1)在AB上取一点D,当AD=_____cm时, △ACD∽△ABC;
(2)在AC的延长线上取一点E,当CE=____cm时, △AEB∽△ABC;
D
E
此时,BE与DC有怎样的位置关系?为什么?
思考探索
1、如图,在△ABC中,D在AB上,
要说明△ACD∽△ABC相似,
已经具备了条件 ,
还需添加的条件是 ,
或 或 .
A
C
D
B
随堂练习
A
E
D
C
B
2、如图, 若AD·AB=AE·AC,则△_______∽△______,
且∠B=_____.
3、如图,已知 ,
试求
的值.
A
D
E
C
B
1. 三角形相似的判定方法有哪些?
2.你有哪些收获?
谢谢合作!
本节随堂练习
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
