圆锥曲线复习[上学期]
图片预览





文档简介
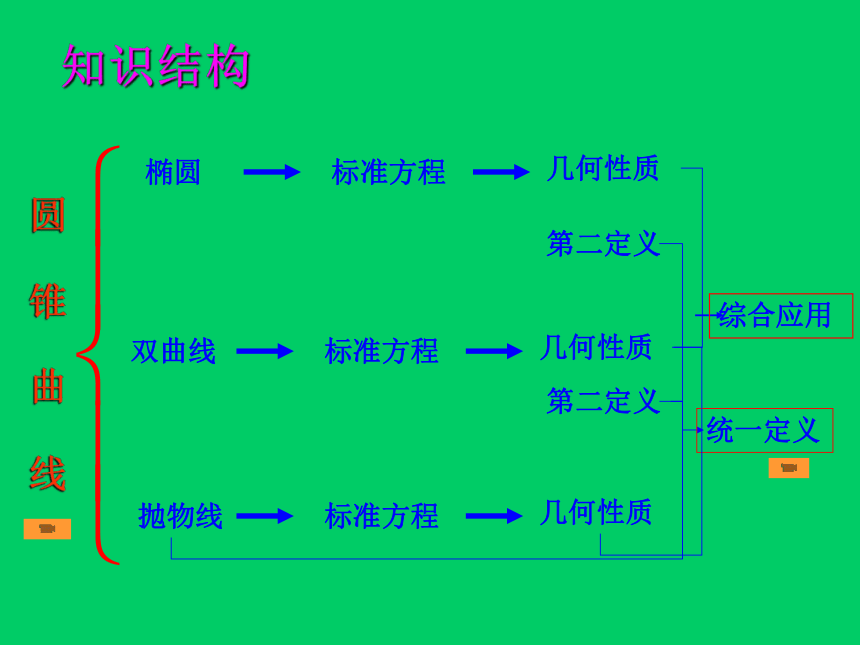
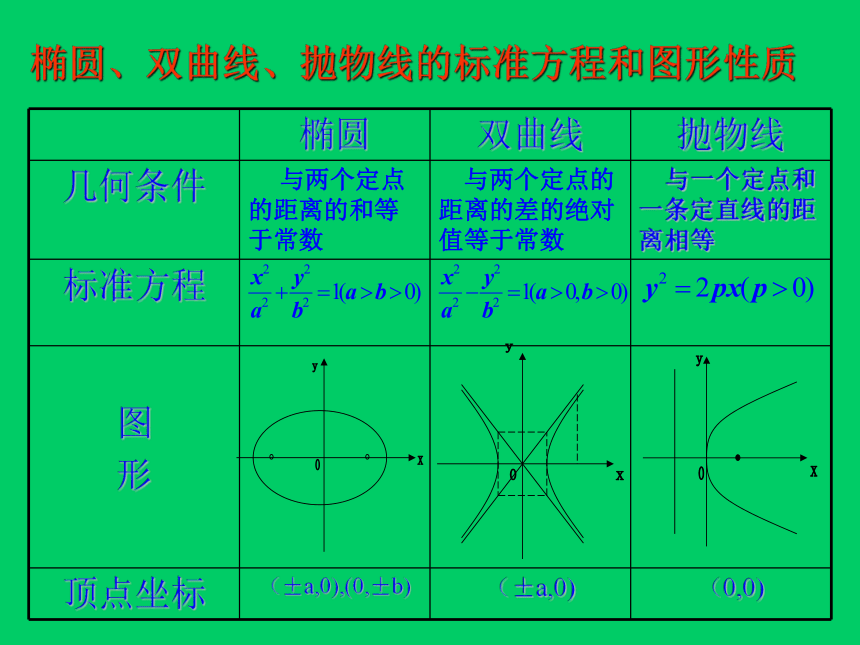
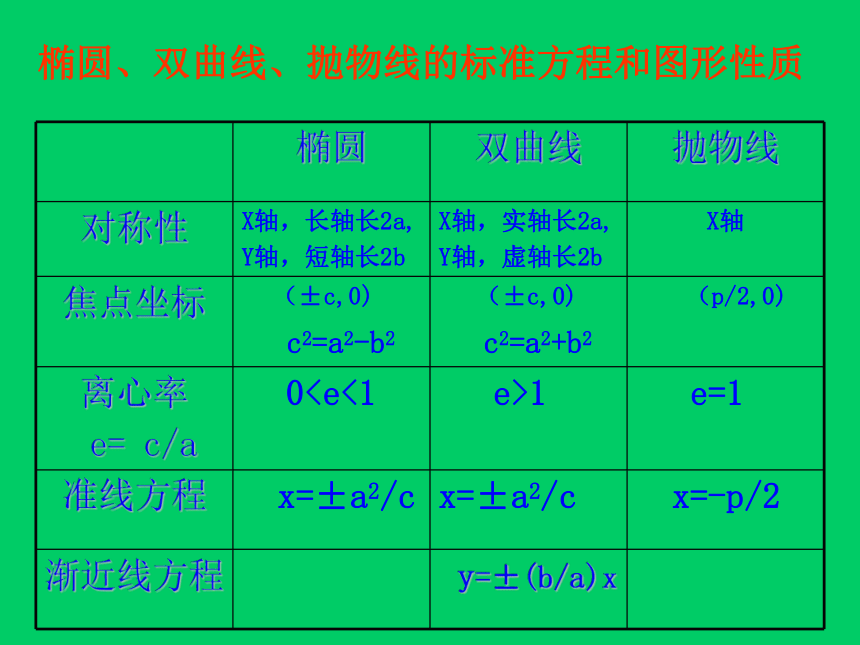
课件27张PPT。圆锥曲线复习课2019年3月16日基础知识系统复习一、学习目标知识结构 圆 锥 曲 线椭圆双曲线抛物线标准方程几何性质标准方程几何性质标准方程几何性质第二定义第二定义统一定义综合应用椭圆、双曲线、抛物线的标准方程和图形性质椭圆、双曲线、抛物线的标准方程和图形性质专题(一)
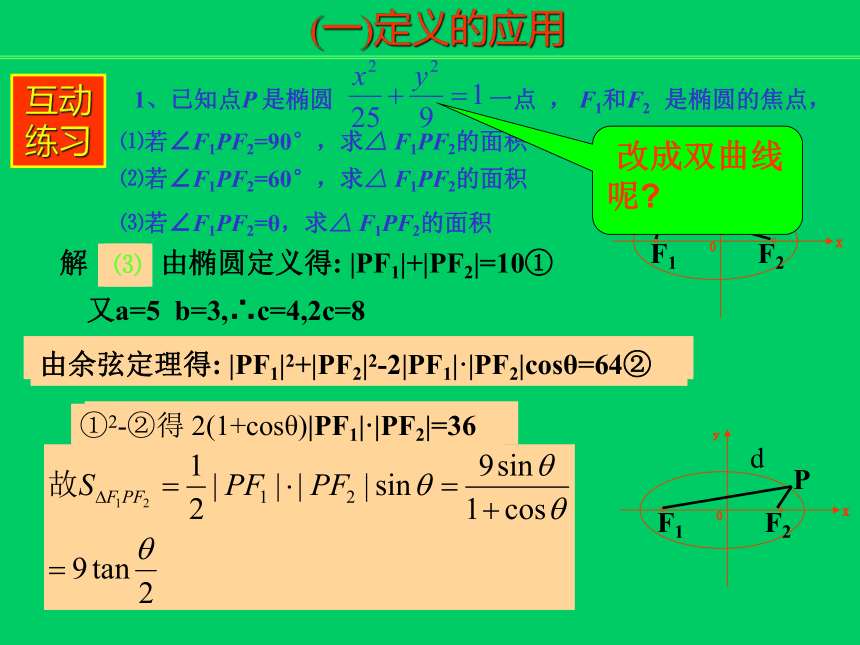
定 义 的 应 用(一)定义的应用互动练习1、已知点P 是椭圆 一点 , F1和F2 是椭圆的焦点,⑴若∠F1PF2=90°,求△ F1PF2的面积⑵若∠F1PF2=60°,求△ F1PF2的面积⑶若∠F1PF2=θ,求△ F1PF2的面积解 ⑴ 由椭圆定义得: |PF1|+|PF2|=10①又a=5 b=3,∴c=4,2c=8
由勾股定理得: |PF1|2+|PF2|2=64②①2-②得 2|PF1|·|PF2|=36由余弦定理得: |PF1|2+|PF2|2-2|PF1|·|PF2|cos60°=64②⑵⑶由余弦定理得: |PF1|2+|PF2|2-2|PF1|·|PF2|cosθ=64②①2-②得 3|PF1|·|PF2|=36①2-②得 2(1+cosθ)|PF1|·|PF2|=36 改成双曲线呢?互动练习2、已知点P 是椭圆 上一点 , F1和F2 是椭圆的左右焦点,求:(1)解法一:(代入法)设P(x,y),易知:c=3, 得F1(-3,0),
由两点间距离公式得:(一)定义的应用互动练习2、已知点P 是椭圆 上一点 , F1和F2 是椭圆的左右焦点,求:(1)解法二:(参数法)设P(5cosθ,4sinθ),易知:c=3, 得F1(-3,0),由两点间距离公式得:(一)定义的应用互动练习(1)解法三:(几何法)设l是已知椭圆与焦点F1相
应的准线,PN⊥l,垂足为N, 由椭圆第二定义得:N(一)定义的应用互动练习2、已知点P 是椭圆 上一点 , F1和F2 是椭圆的左右焦点,求:解 (2) 由椭圆定义得: |PF1|+|PF2|=10思考题:怎样求|PF1|·|PF2|的最小值?
(一)定义的应用3.已知抛物线y=x2,动弦AB的长为2,求AB中点纵坐标的最小值。解:互动练习(一)定义的应用(一)定义的应用互动练习 3. 动点P 到直线 x+4=0 的距离减去它到点M(2,0)的距离之差等于2,则点P 的轨迹是 ( )
A.直线 B.椭圆 C.双曲线 D.抛物线D专题(二)
直线与圆锥曲线的关系1.过点(0,2)与抛物线 只有一个公共点的直线有( )
(A)1条 (B)2条 (C)3条 (D)无数多条 C互动练习互动练习说明:(1)从图形分析,应有四个解 (2)利用方程求解时,应注意对K的讨论 例.直线y=x-2与抛物线y2=2x相交于A、B 求证:OA⊥OB(课本P130例2)。 证法1:将y=x-2代入y2=2x中,得 (x-2)2=2x化简得 x2-6x+4=0解得:则: ∴OA⊥OB证法2:同证法1得方程 x2-6x+4=0由一元二次方程根与系数的关系,可知 x1+x2=6, x1·x2=4 ∴OA⊥OB∵y1=x1-2 , y2=x2-2;∴y1·y2=(x1-2)(x2-2)=x1·x2-2(x1+x2)+4
=4-12+4=-4 例1.直线y=x-2与抛物线y2=2x相交于A、B 求证:OA⊥OB(课本P130例2)。 引伸练习1.直线y=x-2与抛物线y2=2x相交于A、B 求弦长|AB|。 2.直线y=x+b与抛物线y2=2x相交于A、B ,且弦长|AB|=2 ,求该直线的方程. 3.直线l与抛物线y2=2x相交于A、B ,且AB中点的坐标为(3,1), ,求该直线的方程. 4.过抛物线y2=4x的焦点作直线,交此抛物线于A、B两点,求AB中点的轨迹方程. 专题(三)
圆锥曲线方程的求法与讨论求圆锥曲线方程的方法小结1、代入法(用定义)
2、五步法(特别:参数法、相关点法)
3、待定系数法 1. 动点P 到直线 x+4=0 的距离减去它到点M(2,0)的距离之差等于2,则点P 的轨迹是 ( )
A.直线 B.椭圆 C.双曲线 D.抛物线D2.P是双曲线 上任意一点,O为原点,则OP线段中点Q的轨迹方程是( ) 3.和圆x2+y2=1外切,且和x轴相切的动圆圆心O的轨迹方程是 。 x2=2|y|+1B互动练习 例(课本P129例1)一圆与圆x2+y2+6x+5=0外切,同时与圆x2+y2-6x-91=0内切,求动圆圆心的轨迹方程,并说明它是什么曲线。 例(课本P129例1)一圆与圆x2+y2+6x+5=0外切,同时与圆x2+y2-6x-91=0内切,求动圆圆心的轨迹方程,并说明它是什么曲线。解法1:如图:设动圆圆心为P(x,y),半径为R,两已知圆圆心为O1、O2。分别将两已知圆的方程
x2+y2+6x+5=0 x2+y2-6x-91=0
配方,得 (x+3)2+y2=4 (x-3)2+y2=100当⊙P与⊙O1:(x+3)2+y2=4外切时,有|O1P|=R+2 ①
当⊙P与⊙O2:(x-3)2+y2=100内切时,有|O2P|=10-R ②①、②式两边分别相加,得 |O1P|+|O2P|=12即所以,动圆圆心的轨迹是椭圆,它的长轴、短轴分别为 例(课本P129例1)一圆与圆x2+y2+6x+5=0外切,同时与圆x2+y2-6x-91=0内切,求动圆圆心的轨迹方程,并说明它是什么曲线。解法2:同解法1得方程即,动圆圆心P(x,y)到点O1(-3,0)和点O2(3,0)距离的和是12,
所以点P的轨迹是焦点为(-3,0)、(3,0),长轴长等于12的椭圆。∵2c=6 ,2a=12 , ∴ c=3 , a=6 ∴b2=36-9=27于是得动圆圆心的轨迹方程为这个动圆圆心的轨迹是椭圆,它的长轴、短轴分别为 例(课本P129例1)一圆与圆x2+y2+6x+5=0外切,同时与圆x2+y2-6x-91=0内切,求动圆圆心的轨迹方程,并说明它是什么曲线。
定 义 的 应 用(一)定义的应用互动练习1、已知点P 是椭圆 一点 , F1和F2 是椭圆的焦点,⑴若∠F1PF2=90°,求△ F1PF2的面积⑵若∠F1PF2=60°,求△ F1PF2的面积⑶若∠F1PF2=θ,求△ F1PF2的面积解 ⑴ 由椭圆定义得: |PF1|+|PF2|=10①又a=5 b=3,∴c=4,2c=8
由勾股定理得: |PF1|2+|PF2|2=64②①2-②得 2|PF1|·|PF2|=36由余弦定理得: |PF1|2+|PF2|2-2|PF1|·|PF2|cos60°=64②⑵⑶由余弦定理得: |PF1|2+|PF2|2-2|PF1|·|PF2|cosθ=64②①2-②得 3|PF1|·|PF2|=36①2-②得 2(1+cosθ)|PF1|·|PF2|=36 改成双曲线呢?互动练习2、已知点P 是椭圆 上一点 , F1和F2 是椭圆的左右焦点,求:(1)解法一:(代入法)设P(x,y),易知:c=3, 得F1(-3,0),
由两点间距离公式得:(一)定义的应用互动练习2、已知点P 是椭圆 上一点 , F1和F2 是椭圆的左右焦点,求:(1)解法二:(参数法)设P(5cosθ,4sinθ),易知:c=3, 得F1(-3,0),由两点间距离公式得:(一)定义的应用互动练习(1)解法三:(几何法)设l是已知椭圆与焦点F1相
应的准线,PN⊥l,垂足为N, 由椭圆第二定义得:N(一)定义的应用互动练习2、已知点P 是椭圆 上一点 , F1和F2 是椭圆的左右焦点,求:解 (2) 由椭圆定义得: |PF1|+|PF2|=10思考题:怎样求|PF1|·|PF2|的最小值?
(一)定义的应用3.已知抛物线y=x2,动弦AB的长为2,求AB中点纵坐标的最小值。解:互动练习(一)定义的应用(一)定义的应用互动练习 3. 动点P 到直线 x+4=0 的距离减去它到点M(2,0)的距离之差等于2,则点P 的轨迹是 ( )
A.直线 B.椭圆 C.双曲线 D.抛物线D专题(二)
直线与圆锥曲线的关系1.过点(0,2)与抛物线 只有一个公共点的直线有( )
(A)1条 (B)2条 (C)3条 (D)无数多条 C互动练习互动练习说明:(1)从图形分析,应有四个解 (2)利用方程求解时,应注意对K的讨论 例.直线y=x-2与抛物线y2=2x相交于A、B 求证:OA⊥OB(课本P130例2)。 证法1:将y=x-2代入y2=2x中,得 (x-2)2=2x化简得 x2-6x+4=0解得:则: ∴OA⊥OB证法2:同证法1得方程 x2-6x+4=0由一元二次方程根与系数的关系,可知 x1+x2=6, x1·x2=4 ∴OA⊥OB∵y1=x1-2 , y2=x2-2;∴y1·y2=(x1-2)(x2-2)=x1·x2-2(x1+x2)+4
=4-12+4=-4 例1.直线y=x-2与抛物线y2=2x相交于A、B 求证:OA⊥OB(课本P130例2)。 引伸练习1.直线y=x-2与抛物线y2=2x相交于A、B 求弦长|AB|。 2.直线y=x+b与抛物线y2=2x相交于A、B ,且弦长|AB|=2 ,求该直线的方程. 3.直线l与抛物线y2=2x相交于A、B ,且AB中点的坐标为(3,1), ,求该直线的方程. 4.过抛物线y2=4x的焦点作直线,交此抛物线于A、B两点,求AB中点的轨迹方程. 专题(三)
圆锥曲线方程的求法与讨论求圆锥曲线方程的方法小结1、代入法(用定义)
2、五步法(特别:参数法、相关点法)
3、待定系数法 1. 动点P 到直线 x+4=0 的距离减去它到点M(2,0)的距离之差等于2,则点P 的轨迹是 ( )
A.直线 B.椭圆 C.双曲线 D.抛物线D2.P是双曲线 上任意一点,O为原点,则OP线段中点Q的轨迹方程是( ) 3.和圆x2+y2=1外切,且和x轴相切的动圆圆心O的轨迹方程是 。 x2=2|y|+1B互动练习 例(课本P129例1)一圆与圆x2+y2+6x+5=0外切,同时与圆x2+y2-6x-91=0内切,求动圆圆心的轨迹方程,并说明它是什么曲线。 例(课本P129例1)一圆与圆x2+y2+6x+5=0外切,同时与圆x2+y2-6x-91=0内切,求动圆圆心的轨迹方程,并说明它是什么曲线。解法1:如图:设动圆圆心为P(x,y),半径为R,两已知圆圆心为O1、O2。分别将两已知圆的方程
x2+y2+6x+5=0 x2+y2-6x-91=0
配方,得 (x+3)2+y2=4 (x-3)2+y2=100当⊙P与⊙O1:(x+3)2+y2=4外切时,有|O1P|=R+2 ①
当⊙P与⊙O2:(x-3)2+y2=100内切时,有|O2P|=10-R ②①、②式两边分别相加,得 |O1P|+|O2P|=12即所以,动圆圆心的轨迹是椭圆,它的长轴、短轴分别为 例(课本P129例1)一圆与圆x2+y2+6x+5=0外切,同时与圆x2+y2-6x-91=0内切,求动圆圆心的轨迹方程,并说明它是什么曲线。解法2:同解法1得方程即,动圆圆心P(x,y)到点O1(-3,0)和点O2(3,0)距离的和是12,
所以点P的轨迹是焦点为(-3,0)、(3,0),长轴长等于12的椭圆。∵2c=6 ,2a=12 , ∴ c=3 , a=6 ∴b2=36-9=27于是得动圆圆心的轨迹方程为这个动圆圆心的轨迹是椭圆,它的长轴、短轴分别为 例(课本P129例1)一圆与圆x2+y2+6x+5=0外切,同时与圆x2+y2-6x-91=0内切,求动圆圆心的轨迹方程,并说明它是什么曲线。
