苏科版九年级下册 6.5 相似三角形的性质 课件(共13张PPT)
文档属性
| 名称 | 苏科版九年级下册 6.5 相似三角形的性质 课件(共13张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 154.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-29 22:22:04 | ||
图片预览




文档简介
(共13张PPT)
6.5 相似三角形的性质
同学们,我们从相似三角形的定义已经知道相似三角形的对应角相等,对应边成比例。除此以外它还有哪些性质呢?
探究相似三角形的性质
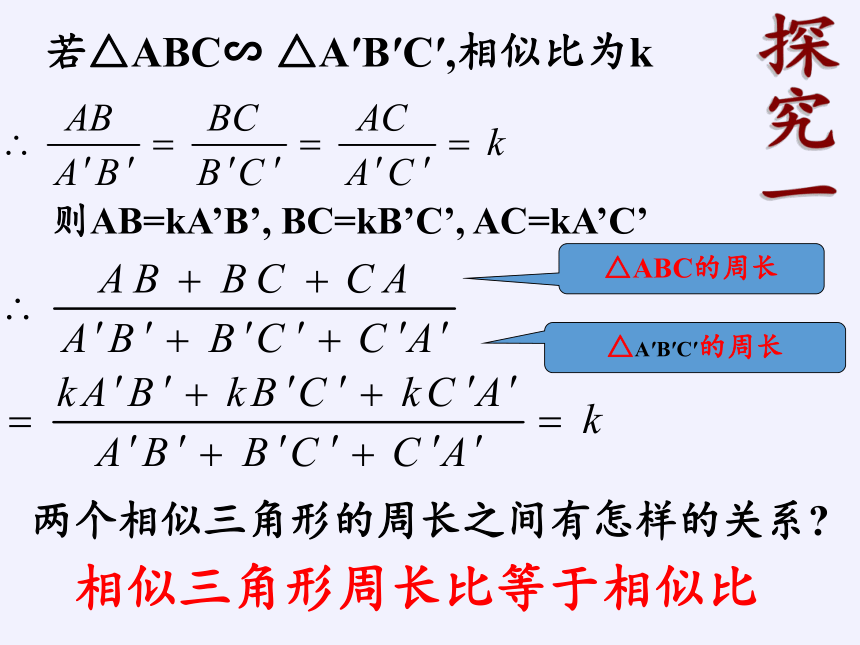
两个相似三角形的周长之间有怎样的关系
若△ABC∽ △A′B′C′,相似比为k
则AB=kA’B’, BC=kB’C’, AC=kA’C’
相似三角形周长比等于相似比
△ABC的周长
△A′B′C′的周长
探究一
相似三角形周长比等于相似比
结论
类似地
相似多边形周长比等于相似比
若四边形ABCD∽ 四边形A1B1C1B1,相似比为k
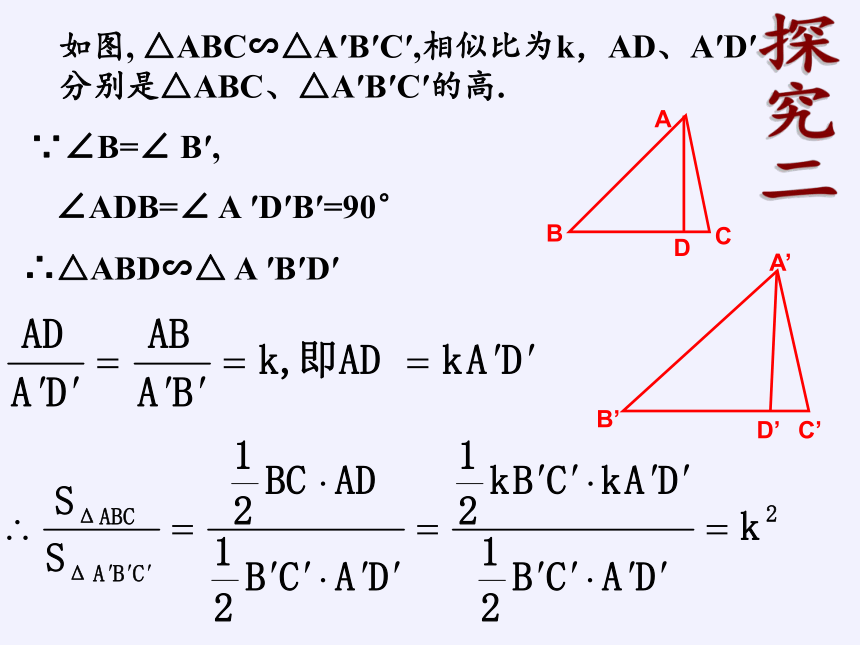
如图, △ABC∽△A′B′C′,相似比为k,AD、A′D′分别是△ABC、△A′B′C′的高.
∵∠B=∠ B′,
∠ADB=∠ A ′D′B′=90°
∴△ABD∽△ A ′B′D′
A
B
C
D
A’
B’
D’
C’
探究二
相似三角形面积比等于相似比平方
结论
类似地
相似多边形面积比等于相似比的平方
1、已知△ABC∽△A′B′C′,且AB=2A′B′,如果△ABC的周长是26cm,那么△A′B′C′的周长是____.
2、两个相似三角形的周长之比为 :2,其面积之比为_____.
3、若点D、E、F为△ABC三边中点,△ABC的面积为12cm2,则△DEF的面积为______.
4、两个相似多边形的一组对应边长分别为35cm,14cm,它们的周长之差为60cm,则这两个多边形的周长之和为_______
初试牛刀
13cm
1:2
3cm2
140cm
例1、在比例尺为1:500的地图上,测得一个三角形地块ABC的周长为12cm,面积为6cm2,求这个地块的实际周长和面积。
例2、已知△ABC∽△DEF,且△ABC面积为81cm2,△DEF的面积为36cm2,且AB=12,求DE
学以致用
例3、如图,把△ABC沿AB边平移到△DEF的位置,它们重叠部分(即图中阴影部分)的面积是△ABC的面积的一半,若AB=2,求此三角形移动距离AD的长.
例4.如图,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CF交AD于F,点E是AB的中点,连接EF。
求证:EF∥BC;
若四边形BDFE的面积为6,求⊿ABD的面积。
能力提升
1、相似三角形对应边的比值为0.4,那么相似比为 , 周长的比为 ,
面积的比为 。
2:5
2:5
4:25
2、若两个相似三角形的面积比为1:4,则这两个相似三角形的周长比是 .
1:2
3、若两个相似多边形的相似比为3:2,已知这两个多边形的周长差为40,则这两个多边形的周长和为 .
200
集中反馈
5、如图在平行四边形ABCD中,AE:AB=1:2 (1)△AEF与△CDF的周长之比____
(2)若△AEF面积为8,则△CDF的面积___
1:2
32
4、两个相似多边形的面积比为9:16,其中较小多边形的周长36,则另一个多边形的周长为 .
集中反馈
48
全等三角形与相似三角形性质比较
全等三角形 相似三角形
对应边相等 对应边的比等于相似比
对应角相等 对应角相等
周长相等 周长的比等于相似比
面积相等 面积的比等于相似比的平方
小结:
1、同步完成导学案巩固练习;
2、完成相似多边形面积比等
于相似比平方的推导过程。
作业:
相似三角形、相似多边形周长比和面积比的性质
设K值法、类比、转化等数学思想方法
谢 谢
6.5 相似三角形的性质
同学们,我们从相似三角形的定义已经知道相似三角形的对应角相等,对应边成比例。除此以外它还有哪些性质呢?
探究相似三角形的性质
两个相似三角形的周长之间有怎样的关系
若△ABC∽ △A′B′C′,相似比为k
则AB=kA’B’, BC=kB’C’, AC=kA’C’
相似三角形周长比等于相似比
△ABC的周长
△A′B′C′的周长
探究一
相似三角形周长比等于相似比
结论
类似地
相似多边形周长比等于相似比
若四边形ABCD∽ 四边形A1B1C1B1,相似比为k
如图, △ABC∽△A′B′C′,相似比为k,AD、A′D′分别是△ABC、△A′B′C′的高.
∵∠B=∠ B′,
∠ADB=∠ A ′D′B′=90°
∴△ABD∽△ A ′B′D′
A
B
C
D
A’
B’
D’
C’
探究二
相似三角形面积比等于相似比平方
结论
类似地
相似多边形面积比等于相似比的平方
1、已知△ABC∽△A′B′C′,且AB=2A′B′,如果△ABC的周长是26cm,那么△A′B′C′的周长是____.
2、两个相似三角形的周长之比为 :2,其面积之比为_____.
3、若点D、E、F为△ABC三边中点,△ABC的面积为12cm2,则△DEF的面积为______.
4、两个相似多边形的一组对应边长分别为35cm,14cm,它们的周长之差为60cm,则这两个多边形的周长之和为_______
初试牛刀
13cm
1:2
3cm2
140cm
例1、在比例尺为1:500的地图上,测得一个三角形地块ABC的周长为12cm,面积为6cm2,求这个地块的实际周长和面积。
例2、已知△ABC∽△DEF,且△ABC面积为81cm2,△DEF的面积为36cm2,且AB=12,求DE
学以致用
例3、如图,把△ABC沿AB边平移到△DEF的位置,它们重叠部分(即图中阴影部分)的面积是△ABC的面积的一半,若AB=2,求此三角形移动距离AD的长.
例4.如图,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CF交AD于F,点E是AB的中点,连接EF。
求证:EF∥BC;
若四边形BDFE的面积为6,求⊿ABD的面积。
能力提升
1、相似三角形对应边的比值为0.4,那么相似比为 , 周长的比为 ,
面积的比为 。
2:5
2:5
4:25
2、若两个相似三角形的面积比为1:4,则这两个相似三角形的周长比是 .
1:2
3、若两个相似多边形的相似比为3:2,已知这两个多边形的周长差为40,则这两个多边形的周长和为 .
200
集中反馈
5、如图在平行四边形ABCD中,AE:AB=1:2 (1)△AEF与△CDF的周长之比____
(2)若△AEF面积为8,则△CDF的面积___
1:2
32
4、两个相似多边形的面积比为9:16,其中较小多边形的周长36,则另一个多边形的周长为 .
集中反馈
48
全等三角形与相似三角形性质比较
全等三角形 相似三角形
对应边相等 对应边的比等于相似比
对应角相等 对应角相等
周长相等 周长的比等于相似比
面积相等 面积的比等于相似比的平方
小结:
1、同步完成导学案巩固练习;
2、完成相似多边形面积比等
于相似比平方的推导过程。
作业:
相似三角形、相似多边形周长比和面积比的性质
设K值法、类比、转化等数学思想方法
谢 谢
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
